↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Many modern machine learning models, especially in graph representation learning, use heterogeneous layers or multiple sub-models. Analyzing their generalization capabilities poses significant challenges. This is particularly true when incorporating topological features, derived via Persistent Homology (PH), into Graph Neural Networks (GNNs). Existing generalization bounds often fail to handle this complexity effectively.
This research introduces a novel compositional PAC-Bayes framework to address this challenge. The key contribution is a general recipe for deriving data-dependent generalization bounds for a broad range of models, including those with heterogeneous layers or PH-based descriptors. The authors demonstrate the efficacy of their method using Persistence Landscapes, and showcase improvements in classifier design through novel regularizers informed by their theoretical bounds on real-world datasets.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working with graph neural networks and topological data analysis. It provides the first data-dependent generalization bounds for persistent homology-enhanced GNNs, a rapidly growing field. This allows for better model design and improved classifier performance, bridging a critical gap in the theoretical understanding of these models. The framework developed is also broadly applicable to heterogeneous neural network architectures, opening up exciting new avenues of research.
Visual Insights#
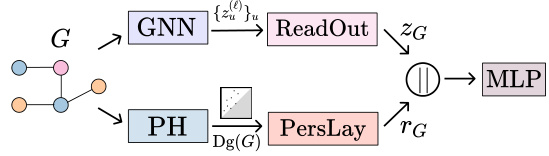
This figure illustrates the parallel mode of integrating persistent homology (PH) into Graph Neural Networks (GNNs). A graph G is input into a GNN, which produces node embeddings {z(l)}u. These embeddings are then used to compute a persistence diagram DG(G) via persistent homology. The persistence diagram is then vectorized using PersLay, resulting in a graph-level representation rG. This representation, along with the graph-level representation zG from the GNN’s readout layer, is concatenated and fed into a Multilayer Perceptron (MLP) for classification.

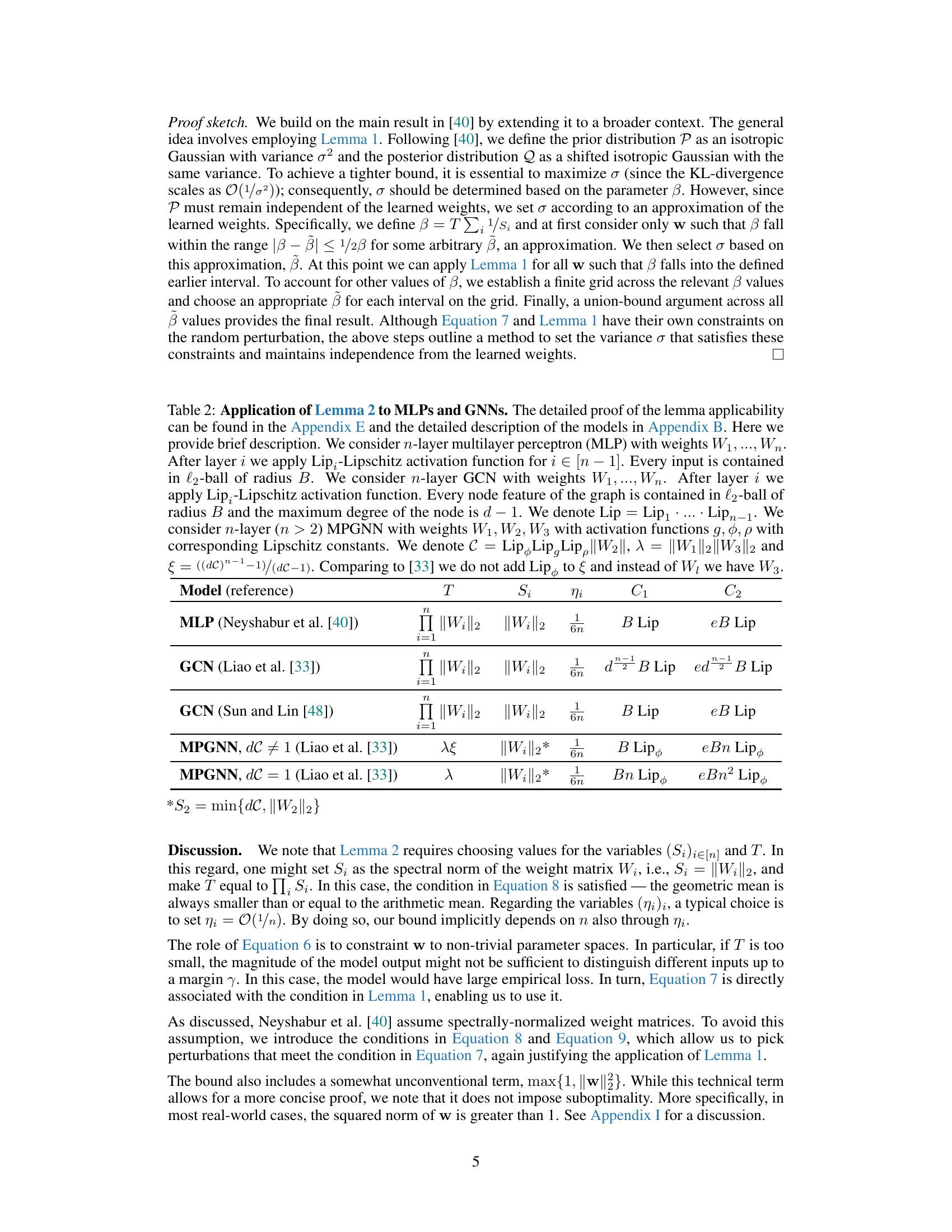
This table shows how Lemma 2 can be applied to obtain generalization bounds for Multilayer Perceptrons (MLPs), Graph Convolutional Networks (GCNs), and Message-Passing Graph Neural Networks (MPGNNs). It lists the parameters (T, Si, Ni, n, C1, C2) from Lemma 2 for each model type, demonstrating how the bounds depend on model architecture and parameters.
In-depth insights#
PAC-Bayes Recipe#
The heading ‘PAC-Bayes Recipe’ suggests a structured approach for deriving generalization bounds, particularly within the context of complex machine learning models. A thoughtful approach would involve examining the conditions under which this recipe is applicable. Key aspects would include the type of models considered (e.g., heterogeneous models with diverse layers, combinations of models), the assumptions made about the data distribution, and the techniques used to manage model complexity. Understanding how the recipe handles model heterogeneity is crucial; it likely involves decomposing the model into manageable sub-components, deriving bounds for each, and then composing these bounds to obtain a bound for the entire system. Data-dependent bounds are important here, implying that the bounds are specific to the given dataset and are potentially tighter than data-independent bounds. The emphasis on a ‘recipe’ suggests a generalized method that can be applied systematically to a range of models, making it a valuable tool for theoretical analysis. Investigating the mathematical rigor underlying the recipe’s steps and the assumptions it relies on would be essential. In addition, exploring the recipe’s effectiveness in practice would involve evaluating its ability to predict generalization performance accurately and how the bounds compare to empirical observations. Ultimately, the usefulness of the ‘PAC-Bayes Recipe’ lies in its ability to provide theoretical guarantees for the generalization performance of complex models while offering a practical pathway for analysis.
PH Generalization#
Analyzing the generalization properties of persistent homology (PH) in machine learning is crucial for reliable model deployment. A key challenge lies in the heterogeneity of modern architectures, often integrating PH with other components like Graph Neural Networks (GNNs). Understanding how the combined model generalizes necessitates moving beyond analyzing individual components, exploring the interaction between topological features from PH and other data representations. A crucial gap in the existing literature is the lack of data-dependent generalization bounds for PH vectorization schemes and PH-augmented GNNs, hindering the design of robust models. This necessitates the development of novel theoretical frameworks, such as compositional PAC-Bayes methods, to analyze heterogeneous models effectively. Such frameworks must account for the interplay between topological features and other model components, enabling the derivation of tight generalization bounds. Furthermore, empirical evaluation on standard datasets should verify the theoretical analysis, demonstrating the correlation between theoretical bounds and actual generalization performance. This holistic approach allows for the design of better regularizers to improve generalization capabilities and build more reliable topological machine learning models.
GNN-PH Bounds#
The hypothetical heading ‘GNN-PH Bounds’ suggests a research area focusing on generalization bounds for Graph Neural Networks (GNNs) augmented with persistent homology (PH) features. This is a significant area because GNNs, while powerful, can suffer from overfitting, and understanding their generalization behavior is crucial. Integrating PH enhances GNNs by capturing topological information, improving their expressiveness and potentially generalization, but this added complexity also makes analyzing generalization bounds more challenging. Therefore, research in ‘GNN-PH Bounds’ would likely involve developing theoretical frameworks, possibly using PAC-Bayes methods, to derive data-dependent generalization bounds. The bounds would consider various factors like the network architecture, PH features’ vectorization methods, and dataset characteristics. Tight bounds are key, as loose bounds offer limited practical value. Empirical validation on real-world datasets would be essential to confirm the theoretical findings. This area of research is important for building robust and reliable GNN-based models, particularly in domains where topological information is significant.
Compositional PB#
The heading “Compositional PB” suggests a method combining different probabilistic models. This approach likely involves a modular design, where individual probabilistic models are treated as components to build more complex systems. The benefits of this approach are numerous: increased model flexibility, improved expressiveness, and enhanced generalizability. By combining simpler models, one can construct sophisticated systems capable of handling diverse data and tackling complex tasks that a single model might struggle with. Data-dependent generalization bounds are crucial in this context to guarantee reliable performance. The methodology likely uses a PAC-Bayes framework, enabling the derivation of generalization bounds for this compositional model. This ensures a theoretical understanding of its generalization capabilities. The “Compositional PB” approach, therefore, represents a powerful paradigm for probabilistic modeling with strong theoretical grounding, offering significant potential for advanced applications.
Regularization Impact#
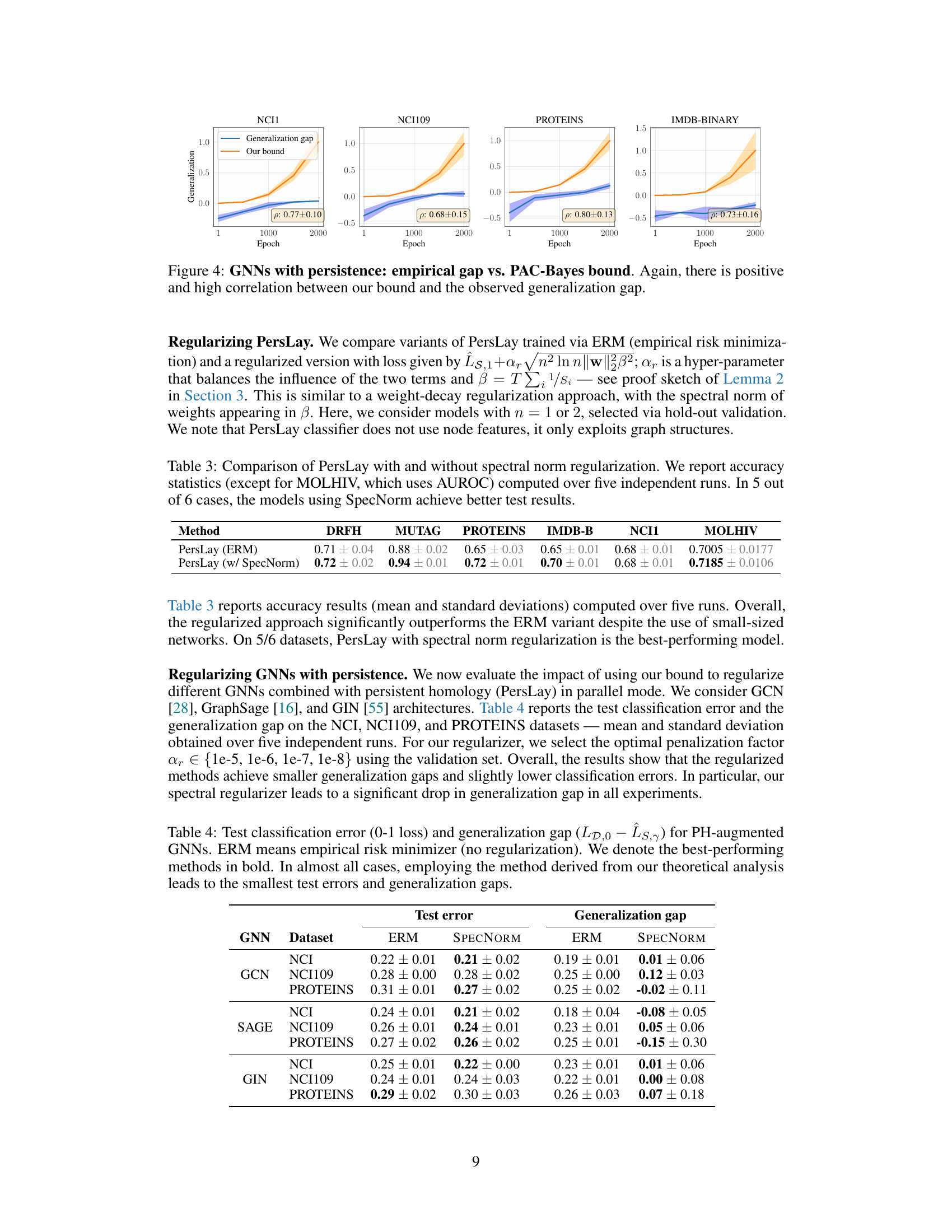
The regularization impact analysis in this research is crucial for enhancing the generalizability of models using persistent homology. The study investigates how regularization, informed by theoretical PAC-Bayes bounds, affects the generalization performance of both PersLay classifiers and GNNs augmented with persistence. Results demonstrate a strong correlation between theoretical bounds and empirical generalization gaps, suggesting that the bounds effectively capture the model’s behavior. This allows for improved classifier design through the development of novel regularization schemes. The experiments show that these novel regularizers significantly outperform empirical risk minimization (ERM) on several real-world datasets. This improvement is especially pronounced in GNNs with persistence, where the regularizers lead to a substantial reduction in both the test error and generalization gap. This finding highlights the importance of data-dependent bounds not just for analysis but also for practical model improvements. The focus on heterogeneous models is a unique contribution, offering a more general framework than those limited to simple architectures. Further research might explore different types of regularizers or investigate the robustness of these findings across different datasets and model complexities.
More visual insights#
More on figures

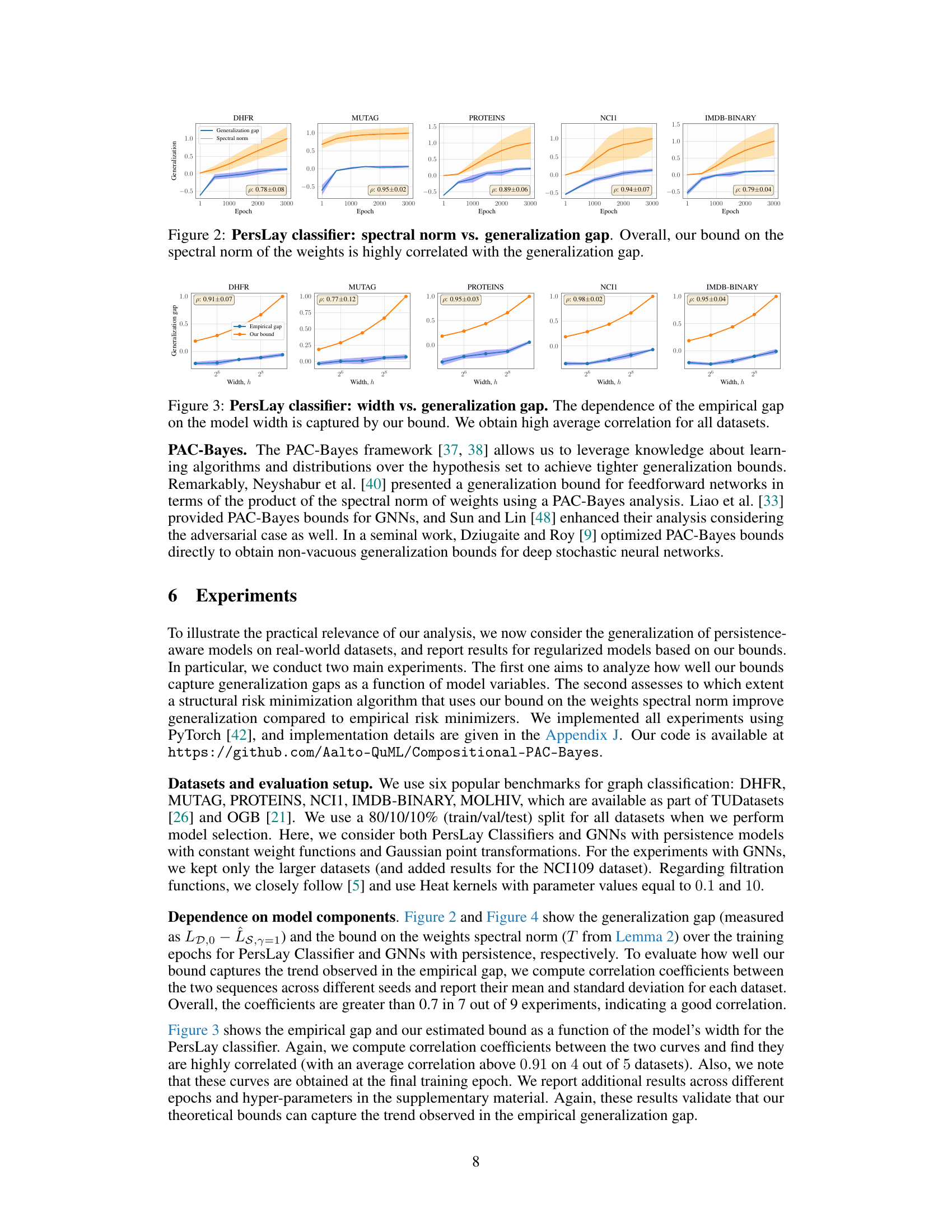
This figure displays the relationship between the spectral norm of the weights in a PersLay classifier and its generalization gap across five different datasets (DHFR, MUTAG, PROTEINS, NCI1, IMDB-BINARY). The plots show the generalization gap (the difference between generalization error and empirical error) and the spectral norm over training epochs. The strong positive correlation (indicated by the ρ values) suggests that the theoretical bound on the spectral norm effectively captures the generalization performance.

This figure shows the relationship between the width of the PersLay classifier model and its generalization gap (difference between the generalization and empirical errors). The plot includes empirical generalization gap and the theoretical bound from the paper’s analysis for five different datasets: DHFR, MUTAG, PROTEINS, NCI1, and IMDB-BINARY. Each dataset has its own subplot, displaying how the generalization gap changes as the model width increases. The high correlation between the empirical results and the theoretical bound suggests the model’s generalization capacity is well-predicted by the proposed framework.

This figure displays the empirical generalization gap (difference between the generalization error and empirical error) against the theoretical PAC-Bayes bound on four datasets (NCI1, NCI109, PROTEINS, IMDB-BINARY). Each subplot shows the trend for a specific dataset, where the x-axis represents the training epochs and the y-axis represents the generalization gap and the theoretical bound. Shaded areas indicate the standard deviation over multiple runs. The correlation coefficient (ρ) between the empirical gap and our theoretical bound is displayed for each dataset, demonstrating a consistently high positive correlation.
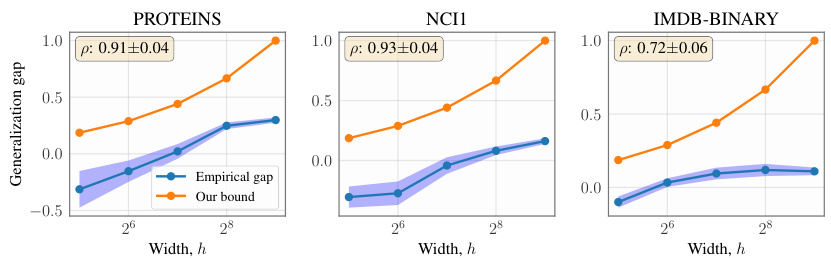
This figure compares the empirical generalization gap with the theoretical bound provided by the authors’ work for a PersLay classifier. The x-axis represents the width (h) of the model, while the y-axis represents the generalization gap. Each dataset (DHFR, MUTAG, PROTEINS, NCI1, IMDB-BINARY) is shown separately, and for each dataset there are two lines: the empirical generalization gap and the theoretical bound. The shaded area represents the standard deviation of the empirical gap across different random seeds. High correlation between the empirical gap and theoretical bounds shows that the theoretical bound accurately captures the trend of generalization performance as the model width changes.
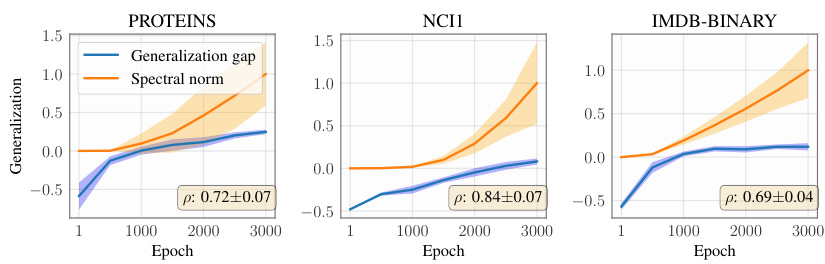
This figure displays the relationship between the spectral norm of weights in a PersLay classifier and its generalization gap across five different datasets (DHFR, MUTAG, PROTEINS, NCI1, IMDB-BINARY). For each dataset, the figure shows the generalization gap (the difference between the generalization error and the empirical error) and the spectral norm of the weights plotted against training epochs. The shaded area represents the standard deviation over multiple runs. The high correlation (rho values) between the spectral norm and generalization gap strongly supports the paper’s claim that the theoretical bounds based on the spectral norm effectively predict the generalization performance of the model.
More on tables

This table shows the application of Lemma 2, a core part of the proposed PAC-Bayes framework, to analyze the generalization performance of various neural network models: MLPs, GCNs, and MPGNNs. It provides the key parameters and bounds derived from applying the Lemma. The table summarizes how the theoretical bounds derived from the Lemma 2 correlate with the model’s parameters for MLPs, GCNs and MPGNNs, highlighting the application of the framework to heterogeneous models. The table also includes references to relevant prior works.
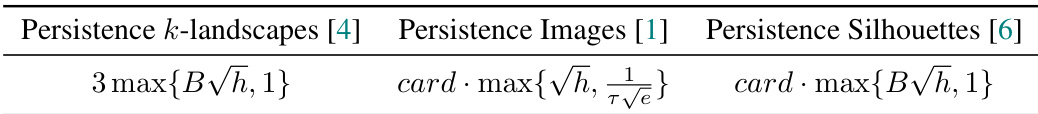
This table summarizes the application of Lemma 2 (a generalized PAC-Bayes recipe for heterogeneous models) to various neural network architectures, including Multilayer Perceptrons (MLPs), Graph Convolutional Networks (GCNs), and Message-Passing Graph Neural Networks (MPGNNs). It shows how to derive the parameters (T, Si, Ni, n, C1, C2) required for Lemma 2, based on existing perturbation analyses found in the cited literature for these models. The table highlights the key differences and similarities in the parameter derivations for different architectures, especially noting the handling of Lipschitz constants and spectral norms.

This table presents a comparison of the performance of PersLay models trained with and without spectral norm regularization. The accuracy (or AUROC for MOLHIV) is reported for six different datasets, with the results averaged over five independent runs. The table demonstrates that spectral norm regularization generally improves the model’s performance.
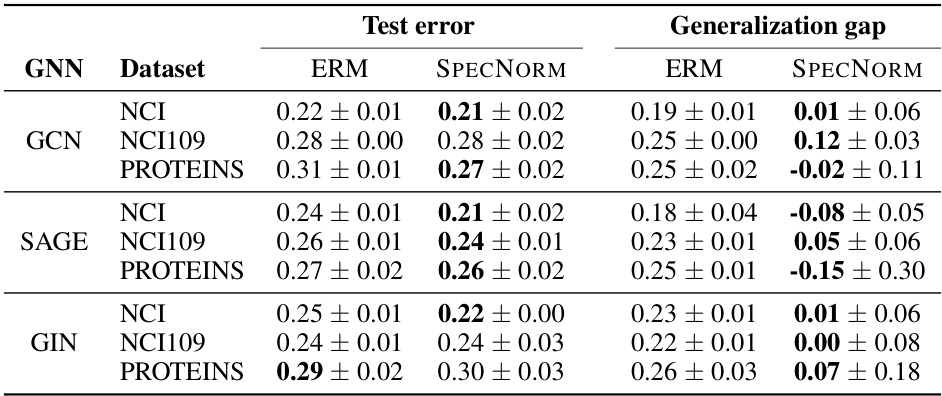
This table presents the results of an experiment comparing the test classification error and generalization gap of three different graph neural networks (GCN, SAGE, GIN) augmented with persistent homology, using both empirical risk minimization (ERM) and a spectral norm regularization method. The spectral norm regularization, informed by the theoretical bounds derived in the paper, shows improvements in both test error and generalization gap across multiple datasets.

This table summarizes the application of Lemma 2 (a general recipe for obtaining PAC-Bayes bounds for heterogeneous models) to specific neural network architectures: MLPs, GCNs, and MPGNNs. It provides the key parameters (T, Si, Ni, n) required for calculating the generalization bounds for each model based on the conditions described in Lemma 2. The table also references relevant previous work that supports the analysis.

This table presents the application of Lemma 2 (a generalized PAC-Bayes framework) to analyze the generalization of Multilayer Perceptrons (MLPs) and Graph Neural Networks (GNNs). It shows how to derive generalization bounds for these models by defining specific parameters (T, Si, Ni, n, C1, C2) within the Lemma 2 framework. The table also compares the results with prior works ([40], [33]) highlighting that the new approach provides generalization bounds even for models with non-homogeneous layers and different activation functions.
This table shows how Lemma 2, a general recipe for obtaining PAC-Bayes bounds for heterogeneous models, is applied to specific neural network architectures (MLPs, GCNs, and MPGNNs). It summarizes the parameters (T, Si, Ni) required for each model type to satisfy the conditions of Lemma 2, enabling the derivation of generalization bounds. The table also highlights differences in the required parameters based on the activation function and the type of GNN architecture used.
Full paper#