↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Graph anomaly detection (GAD) is crucial but challenging. Existing methods often rely on fully unsupervised settings, ignoring potentially valuable information from labeled normal nodes. This is especially problematic in real-world scenarios where obtaining fully labeled data is expensive. The current unsupervised GAD methods also struggle to effectively utilize limited normal node information.
This paper introduces GGAD, a novel Generative GAD approach designed for semi-supervised settings. GGAD cleverly generates “outlier nodes” which act as pseudo-anomaly nodes in the training process. These outlier nodes are generated by leveraging two key properties of real anomaly nodes: asymmetric local affinity and egocentric closeness. This allows GGAD to significantly outperform state-of-the-art unsupervised and semi-supervised methods across various real-world datasets, demonstrating its practical value and effectiveness in handling limited labeled data.
Key Takeaways#
Why does it matter?#
This paper is important because it tackles a practical yet under-explored semi-supervised graph anomaly detection (GAD) scenario, where only a small percentage of normal nodes are labeled. This is highly relevant to real-world applications where fully labeled data is scarce and costly to obtain. The proposed GGAD method significantly outperforms existing techniques, establishing a new benchmark and paving the way for more efficient and practical GAD solutions. Its generative approach and use of priors are novel and could inspire further research in semi-supervised learning for graphs and other non-Euclidean data.
Visual Insights#

This figure illustrates the concept of GGAD and compares it with AEGIS. The left panel shows an example graph where normal nodes have stronger connections to other normal nodes than to anomalous nodes. GGAD aims to generate synthetic ‘outlier’ nodes that mimic the characteristics of true anomalies, both structurally (local affinity) and representationally (features). The right panel contrasts GGAD with AEGIS, highlighting how AEGIS-generated outliers poorly match the distribution and local structure of real anomalies, while GGAD’s approach produces more realistic synthetic data.

This table presents the AUROC and AUPRC scores achieved by GGAD and twelve other graph anomaly detection (GAD) methods across six real-world datasets. The results are categorized into unsupervised and semi-supervised approaches, reflecting whether or not labeled normal nodes were used during training. The best performing method for each dataset is highlighted in bold, with the second-best underlined. A slash indicates that a particular method was unable to process the DGraph dataset due to computational limitations.
In-depth insights#
Semi-Supervised GAD#
Semi-supervised graph anomaly detection (GAD) presents a practical approach that contrasts with fully unsupervised methods. Leveraging even a small percentage of labeled normal nodes significantly boosts performance. This approach acknowledges the real-world constraint of readily available normal node labels, unlike the often unrealistic assumption of completely unlabeled graphs in unsupervised GAD. The key challenge lies in effectively utilizing this partial label information without ground truth anomaly labels. This necessitates innovative techniques, such as generative models which create synthetic anomaly data, enabling better training and improving the accuracy of anomaly detection. Asymmetric local affinity and egocentric closeness of anomaly nodes are identified as important prior knowledge for improving the quality and relevance of the generated synthetic anomalies. The success of semi-supervised GAD hinges on the effective combination of discriminative and generative approaches, leveraging the strengths of both to achieve superior anomaly identification in real-world graph datasets. The practical implications are significant for numerous domains where labeled normal data is easily obtainable but complete anomaly labeling is expensive or impossible.
Generative GGAD#
Generative GGAD presents a novel approach to semi-supervised graph anomaly detection by leveraging the power of generative models. The core idea is to generate synthetic “outlier nodes” that mimic the characteristics of real anomalies, thus providing effective negative samples for training a one-class classifier on the labeled normal nodes. This cleverly addresses the challenge of limited ground truth anomaly data in semi-supervised settings. GGAD incorporates two key priors about anomalies: asymmetric local affinity (anomalies have weaker connections with normal nodes) and egocentric closeness (anomalies share similar feature representations with nearby normal nodes). These priors guide the outlier generation process, ensuring the synthetics are realistic and enhance model performance. The effectiveness of GGAD is demonstrated through extensive experiments, showcasing its superior performance compared to existing unsupervised and semi-supervised methods, particularly when the number of labeled normal nodes is limited. This approach highlights the potential of generative models to address data scarcity issues in semi-supervised learning contexts, offering a significant advance in graph anomaly detection.
Asymmetric Affinity#
The concept of “Asymmetric Affinity” in graph anomaly detection is a powerful idea that leverages the inherent structural differences between normal and anomalous nodes. Normal nodes tend to exhibit strong, reciprocal connections with their neighbors, reflecting a cohesive community structure. In contrast, anomalous nodes often show weaker or asymmetric relationships, with connections that are less balanced or reciprocal. This asymmetry arises because anomalies often reside at the periphery of the graph or disrupt the typical patterns of connectivity within communities. Exploiting this asymmetry provides a way to identify anomalies without needing complete ground-truth labeling. Algorithms can be designed to score nodes based on the strength and reciprocity of their connections, with nodes exhibiting significantly asymmetric relationships flagged as potential anomalies. This approach is particularly useful in semi-supervised settings where only a small subset of nodes are labeled as normal, as it doesn’t rely on full knowledge of the anomalous nodes. However, challenges remain in precisely defining and quantifying this asymmetry, especially as graph structures and relationships become complex. Further research could explore ways to combine this approach with other anomaly detection techniques for improved accuracy and robustness. The effectiveness of this approach would likely depend on the type of graph and how distinctly the anomalous nodes deviate from the normal patterns of connectivity.
Egocentric Closeness#
The concept of “Egocentric Closeness” in anomaly detection within graph structures is a novel approach focusing on the subtle similarities between anomalous nodes and their normal counterparts. It posits that anomalies, despite their deviant behavior, often maintain a degree of closeness in feature representation to their normal neighbors. This closeness isn’t necessarily based on direct connections but rather on the overall similarity of their feature vectors. The underlying idea is that the anomaly might subtly camouflage itself, making it difficult to distinguish solely based on local graph structures. This notion of subtle similarity is crucial as it contrasts the typical assumption that anomalies are vastly different from normal data points. GGAD uses this principle to generate more realistic pseudo-anomalies, which are vital for training a one-class classifier. By ensuring the generated outliers possess similar features to normal nodes while still maintaining separability, the model can achieve superior performance. The efficacy of this approach hinges on the inherent characteristics of the data: the success depends on the degree to which anomalies exhibit this ’egocentric closeness’ and how distinct they are from normal nodes in other aspects. This approach is a key advancement in semi-supervised anomaly detection, offering a new way to leverage the limited availability of labeled data.
Future Research#
Future research directions stemming from this work on generative semi-supervised graph anomaly detection (GAD) could explore several promising avenues. Improving the outlier generation process is crucial; investigating alternative generative models beyond the current approach, and incorporating more sophisticated graph structural priors could enhance outlier realism and effectiveness. A key area is handling imbalanced datasets: current methods might underperform with highly skewed class distributions. Future research should focus on techniques robust to such imbalances. Finally, extending the framework to dynamic graphs is vital for broader applicability. Real-world graphs are often time-evolving, so adapting the model to incorporate temporal dependencies and handle node/edge additions/deletions would significantly increase its utility. In addition, a thorough evaluation on a wider range of datasets would strengthen the conclusions. Investigating the interpretability of the anomaly scores produced by the model would also be valuable, allowing for greater trust and understanding of its predictions. Exploring alternative methods for assessing and comparing the effectiveness of semi-supervised techniques, beyond simple comparisons with purely unsupervised approaches, would also be helpful.
More visual insights#
More on figures
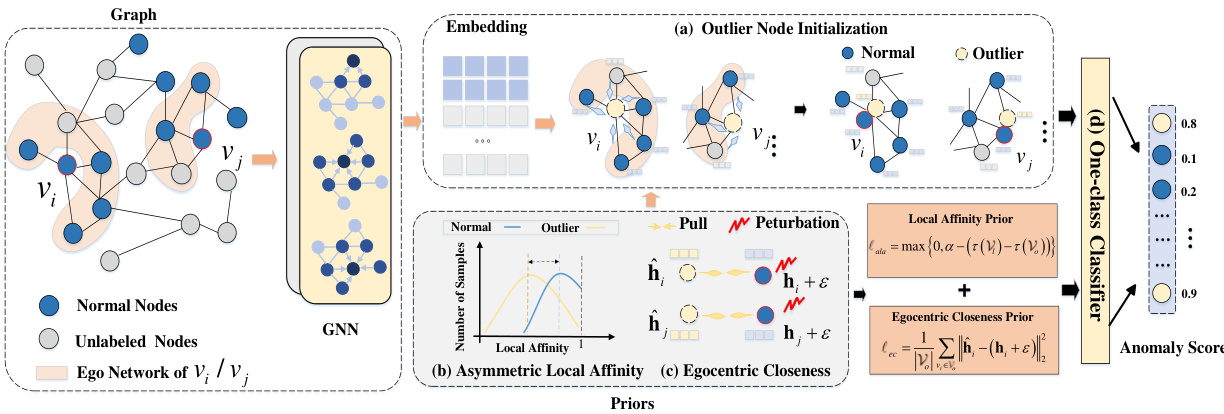
This figure illustrates the overall framework of the GGAD model. First, it initializes outlier nodes using the feature representations of the ego networks of labeled normal nodes. Then, it refines these initial outliers by incorporating two important priors about anomaly nodes: asymmetric local affinity and egocentric closeness. These priors are enforced through loss functions that guide the outlier generation process. Finally, these generated outlier nodes are used as negative samples to train a discriminative one-class classifier on the labeled normal nodes, producing anomaly scores.

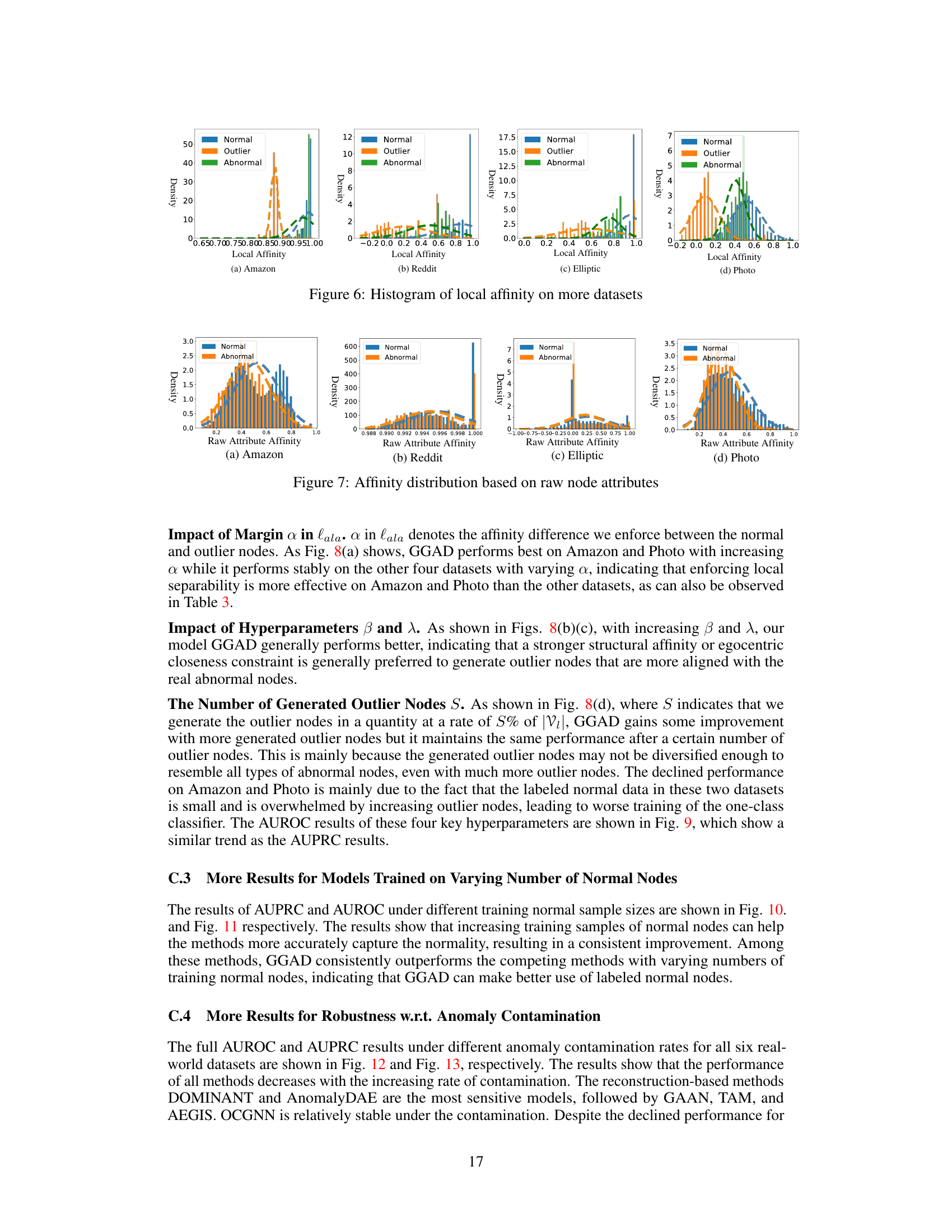
This figure compares the performance of GGAD and its variants (using only local affinity prior or only egocentric closeness prior) in terms of node representation visualization (t-SNE) and local affinity distribution. The visualization shows how well the generated outlier nodes (by GGAD and its variants) match the real anomaly nodes in the feature space and in their local graph structure. The histograms show how the local affinity of the generated outliers is different from the real anomalies and normal nodes, highlighting the effectiveness of GGAD in generating more realistic outlier nodes.
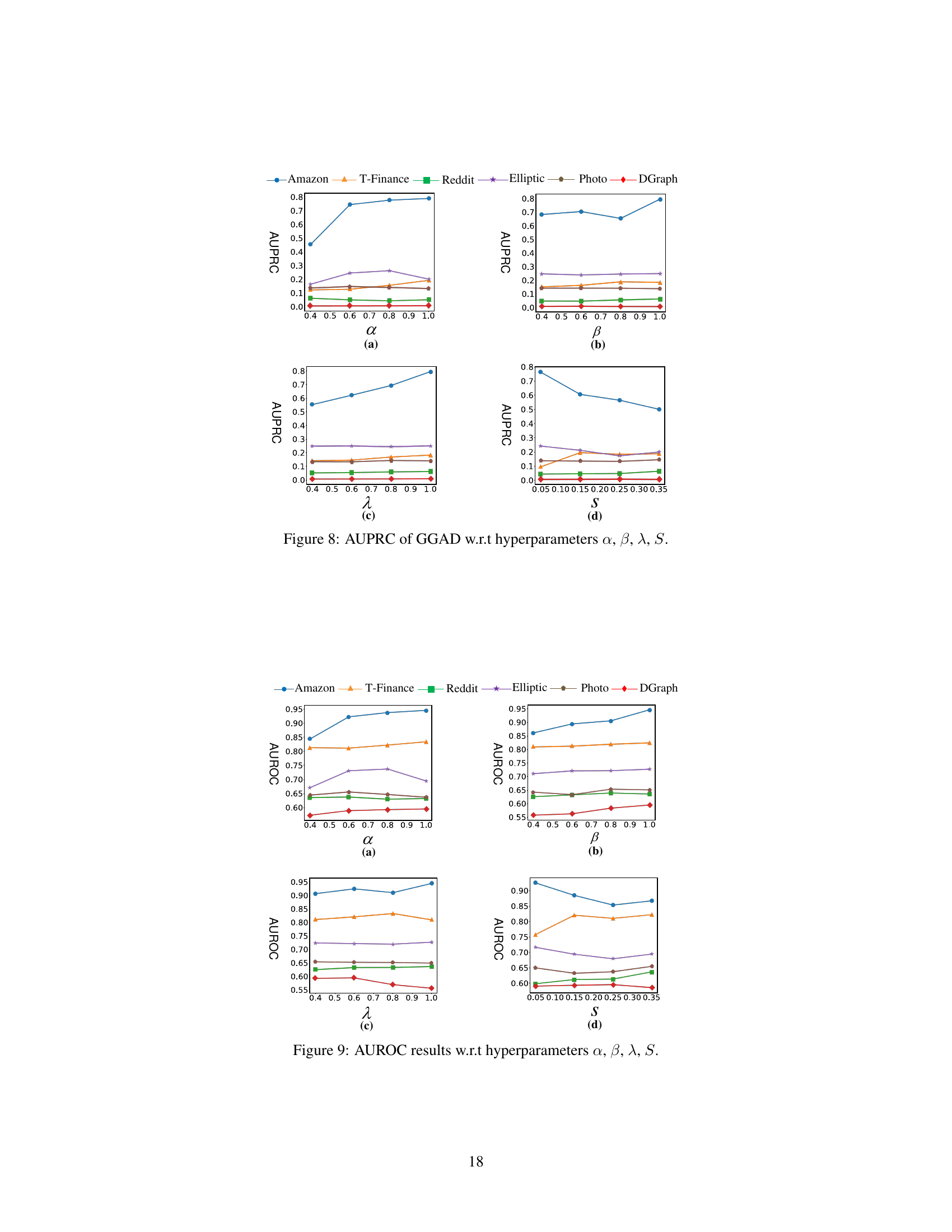
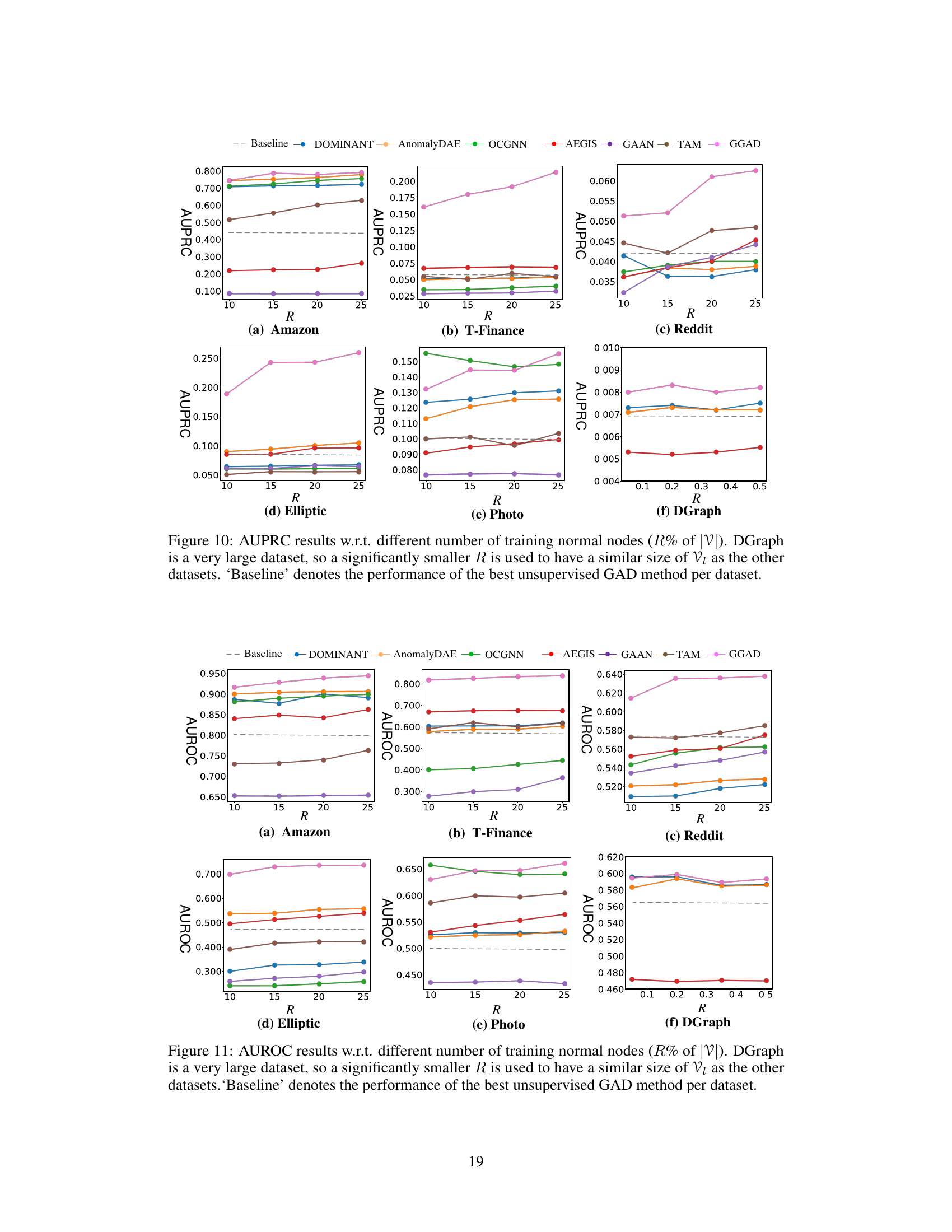
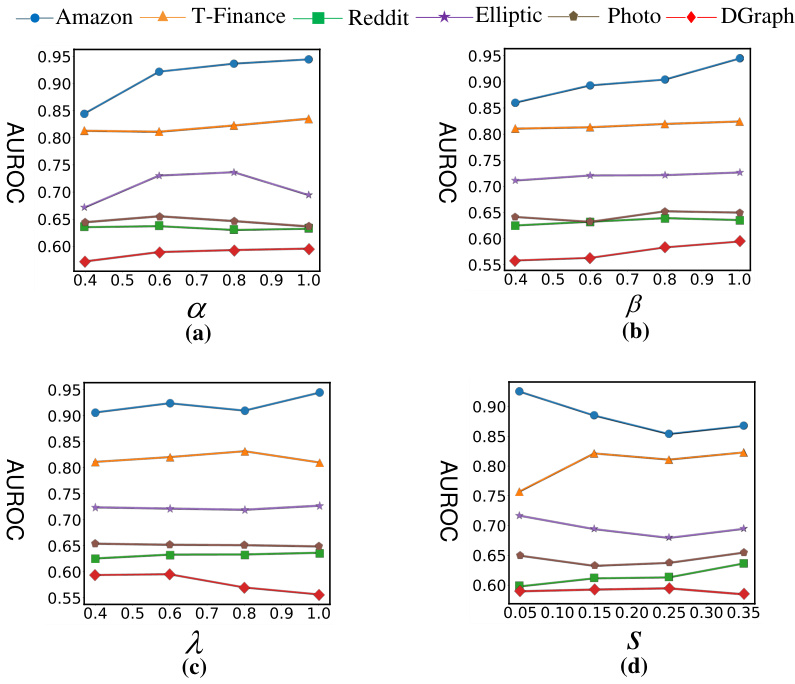
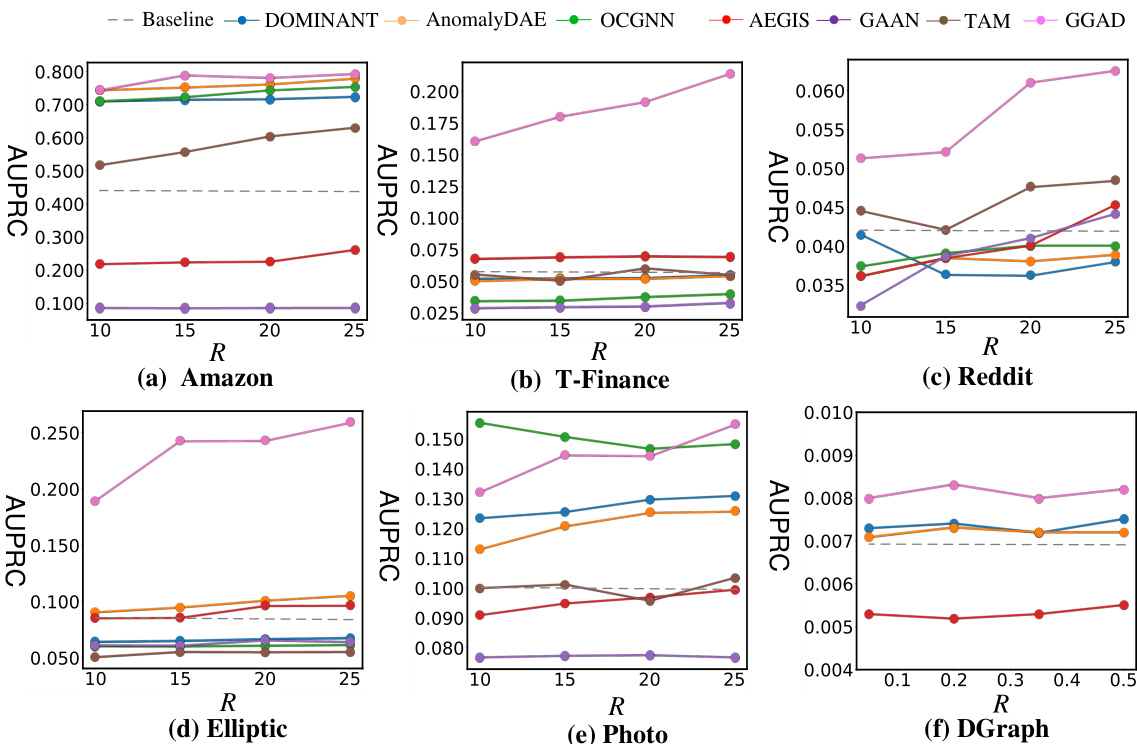
The figure shows the AUPRC (Area Under the Precision-Recall Curve) performance of GGAD and other methods across six datasets as the percentage of training normal nodes (R%) varies. It demonstrates how the performance changes with different sizes of training data, illustrating GGAD’s effectiveness in leveraging labeled normal nodes.

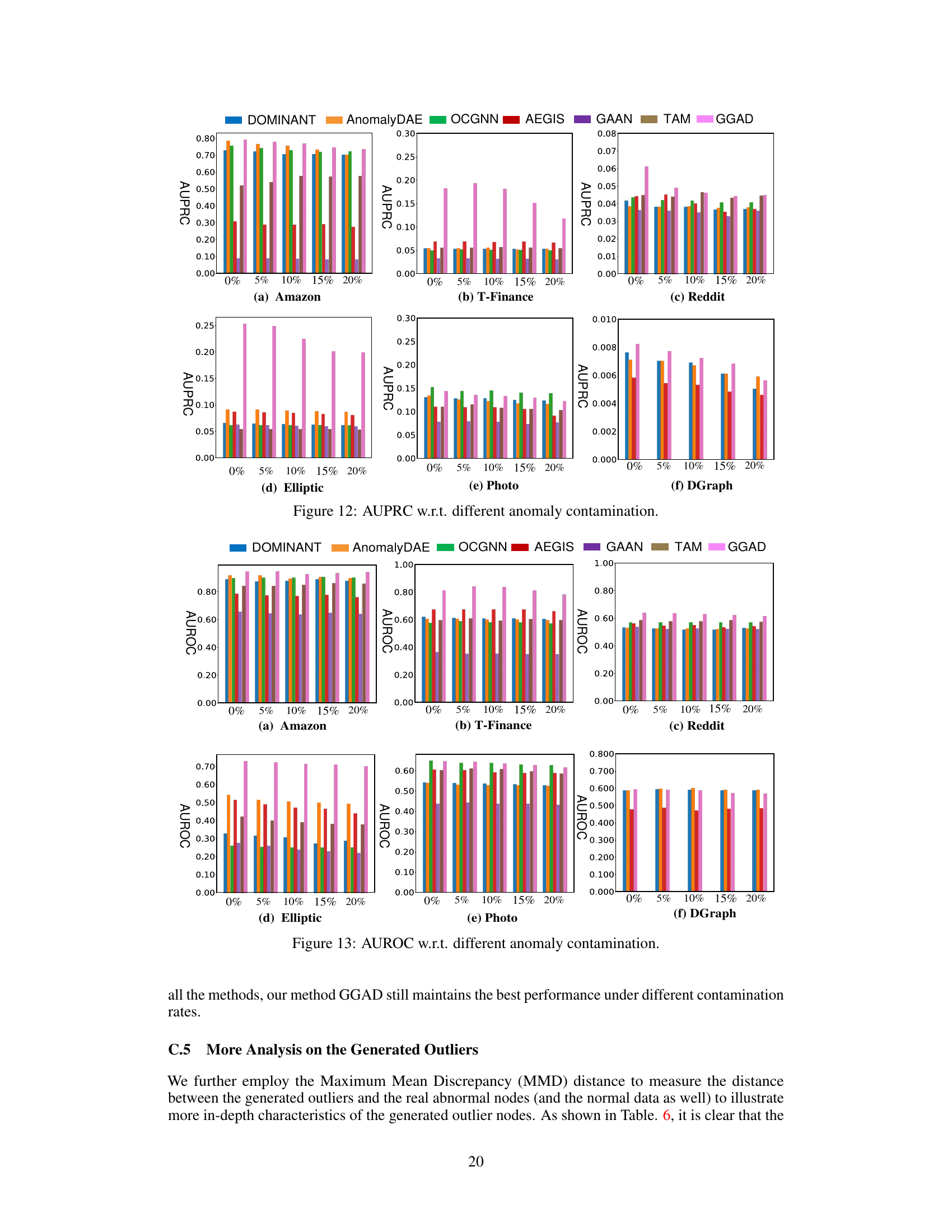
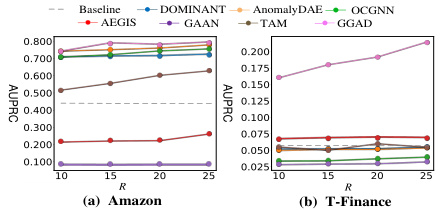
This figure shows the AUPRC (Area Under the Precision-Recall Curve) results for different anomaly contamination rates on two datasets: Amazon and T-Finance. It demonstrates the robustness of GGAD (Generative Graph Anomaly Detection) compared to other methods (DOMINANT, AnomalyDAE, OCGNN, AEGIS, GAAN, TAM) when dealing with contaminated data, illustrating the impact of having incorrect labels in training data on model performance. GGAD consistently shows higher AUPRC, maintaining its effectiveness even as more anomalies are introduced in training data.

This figure visualizes the node representations and local affinity distributions generated by GGAD and its variants (using only local affinity loss, only egocentric closeness loss). The t-SNE plots (a-c) show how the different methods position normal, outlier, and abnormal nodes in the feature space. The histograms (d-f) show the distribution of local affinity values for each node type. The comparison highlights the effectiveness of GGAD in generating outliers that closely resemble the characteristics of true anomalies.

This figure compares the performance of GGAD with two of its variants using t-SNE visualization and histograms of local affinity. The t-SNE visualizations show the distribution of normal, outlier, and abnormal nodes in the feature representation space. The histograms illustrate the distribution of local affinity scores for normal, outlier, and abnormal nodes. By comparing these visualizations and histograms, the figure showcases how GGAD generates outlier nodes that closely resemble the characteristics of abnormal nodes, particularly in terms of both feature representation and local affinity.

This figure illustrates the GGAD approach. It begins by initializing outlier nodes based on the feature representations of neighboring nodes to a labeled normal node. Then, it leverages two priors about anomaly nodes (asymmetric local affinity and egocentric closeness) to refine these outlier nodes, aligning them more closely with real anomalies. Finally, these generated outlier nodes serve as negative samples to train a one-class classifier using labeled normal nodes.
This figure illustrates the GGAD approach. It begins by initializing outlier nodes based on the features of labeled normal nodes’ ego networks (a). Two loss functions then refine the outlier nodes: one incorporating asymmetric local affinity (b), and the other employing egocentric closeness (c). The resulting refined outliers (d) serve as negative samples for training a one-class classifier.
This figure illustrates the GGAD approach for semi-supervised graph anomaly detection. It shows the process of initializing outlier nodes based on the features of labeled normal nodes’ ego networks, then incorporating two anomaly priors (asymmetric local affinity and egocentric closeness) to optimize these outlier nodes. Finally, these optimized outliers are used as negative samples to train a one-class classifier on the normal nodes.

This figure illustrates the GGAD (Generative Graph Anomaly Detection) approach. It starts by initializing outlier nodes using the features of the labeled normal nodes’ ego networks. These initial outliers are then refined using two key priors: asymmetric local affinity (making sure the outliers’ local connections are weaker than those of normal nodes) and egocentric closeness (ensuring outliers’ feature representations are close to similar normal nodes). Finally, these optimized outliers serve as negative samples to train a one-class classifier on the normal nodes.

This figure illustrates the overall process of the GGAD model. It starts by initializing outlier nodes based on the features of labeled normal nodes’ ego networks. Then, the model leverages two priors on anomaly nodes (asymmetric local affinity and egocentric closeness) to optimize these outlier nodes. Finally, the optimized outlier nodes are used as negative examples to train a one-class classifier.

This figure illustrates the GGAD approach. It starts by initializing outlier nodes based on the features of labeled normal nodes’ ego networks. Then, it refines these outlier nodes using two priors: asymmetric local affinity (making outlier nodes less similar to their neighbors than normal nodes) and egocentric closeness (pulling outlier node features towards similar normal nodes). Finally, these refined outlier nodes are used as negative samples to train a one-class classifier on the labeled normal nodes.

This figure illustrates the GGAD (Generative Graph Anomaly Detection) approach. It starts by initializing outlier nodes using the feature representations of the ego networks (neighbors) of labeled normal nodes. Then, two key priors about anomaly nodes are incorporated: asymmetric local affinity (making sure outliers have weaker local affinity than normal nodes) and egocentric closeness (making sure outliers have similar feature representations to normal nodes with similar local structure). Finally, these optimized outlier nodes serve as negative samples to train a one-class classifier on the labeled normal nodes.
More on tables
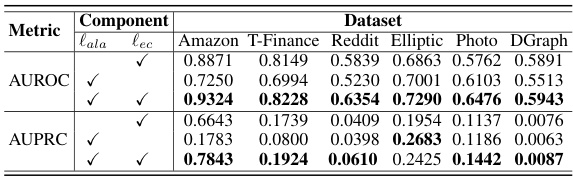
This table presents the performance of GGAD and 12 other graph anomaly detection (GAD) methods across six real-world datasets. The metrics used are AUROC (Area Under the Receiver Operating Characteristic curve) and AUPRC (Area Under the Precision-Recall curve). The table highlights the best-performing method for each dataset in bold and the second-best in underline. It also shows that GGAD significantly outperforms existing unsupervised and semi-supervised GAD methods. The ‘/’ indicates when a method failed to process the DGraph dataset.

This table presents the results of the proposed GGAD model and 12 other state-of-the-art (SOTA) GAD methods on six real-world datasets. The metrics used to evaluate performance are AUROC (Area Under the Receiver Operating Characteristic curve) and AUPRC (Area Under the Precision-Recall curve). The best-performing model for each dataset is highlighted in bold, and the second-best is underlined. The table shows that GGAD significantly outperforms other methods on most datasets and demonstrates the benefit of using a semi-supervised approach compared to purely unsupervised techniques. The ‘/’ indicates that the specific method does not work with that specific dataset.

This table presents the AUROC (Area Under the Receiver Operating Characteristic curve) and AUPRC (Area Under the Precision-Recall curve) scores achieved by GGAD and 12 other state-of-the-art anomaly detection methods across six different real-world graph datasets. The best performing method for each dataset is highlighted in bold, and the second-best is underlined. The ‘/’ symbol indicates that a particular method was unable to process the DGraph dataset due to its size or other limitations. This table allows comparison of GGAD’s performance against existing techniques in both unsupervised and semi-supervised settings, providing a comprehensive evaluation of its effectiveness across various datasets and model types.

This table presents the performance of GGAD and 12 other methods (six unsupervised and six semi-supervised) across six graph anomaly detection datasets. The Area Under the Receiver Operating Characteristic curve (AUROC) and the Area Under the Precision-Recall Curve (AUPRC) are used as evaluation metrics. The best performing method for each dataset is shown in boldface, while the second-best is underlined. A ‘/’ indicates that the method was not evaluated on the DGraph dataset due to its computational constraints.

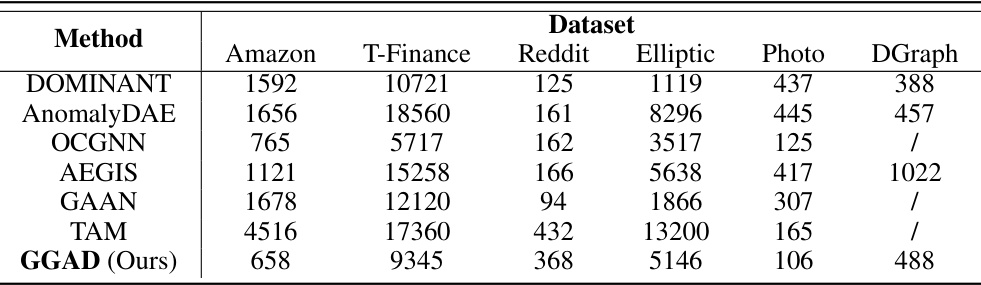
This table presents the Maximum Mean Discrepancy (MMD) distances between the generated outlier nodes and both the real abnormal nodes and the normal nodes. MMD measures the dissimilarity between the probability distributions of the two node sets. Lower MMD indicates higher similarity. The results show that the generated outlier nodes have much smaller MMD distances to the real abnormal nodes than the normal nodes, indicating that the generated outlier nodes successfully assimilate the real anomalies.
This table presents the AUROC and AUPRC scores achieved by GGAD and twelve other state-of-the-art anomaly detection methods across six real-world graph datasets. The best performing method for each dataset is highlighted in bold, with the second-best underlined. The table allows for a comparison of GGAD’s performance against both unsupervised and semi-supervised methods, demonstrating its superiority.
Full paper#