↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Slow inference is a major bottleneck in using diffusion transformers, which are powerful generative models. Existing approaches for acceleration mainly target reducing model size or number of sampling steps, but those often reduce image quality. This paper addresses this issue by identifying and removing redundant computations.
The authors propose Learning-to-Cache (L2C), a novel technique that learns to cache and reuse intermediate computations across different steps within the diffusion process. L2C leverages the inherent structure of transformer networks and treats each layer as a unit for caching. By using a differentiable optimization objective, L2C outperforms existing methods in terms of speed and image quality, demonstrating that a substantial portion of computations in diffusion transformers can be efficiently removed.
Key Takeaways#
Why does it matter?#
This paper is important because it presents a novel method to significantly speed up the inference of diffusion transformers, a crucial architecture in various generative AI tasks. The proposed approach, Learning-to-Cache, achieves this speedup by strategically caching and reusing computations from previous steps. This is particularly relevant given the increasing computational demands of large-scale generative AI models, where faster inference is essential for both research and deployment. The findings could inspire new techniques for optimizing the efficiency of other transformer-based models. This work opens up avenues for further research into dynamic computation graphs, improving the efficiency of complex AI systems.
Visual Insights#

This figure shows image generation results from two different diffusion transformer models: DiT-XL/2 and U-ViT-H/2. Subfigure (a) displays 512x512 images generated using DiT-XL/2 and the DDIM sampler, while subfigure (b) shows 256x256 images generated using U-ViT-H/2 and the DPM-Solver-2 sampler. Both used 50 noise-removing steps (NFEs). The figure highlights the visual quality achieved by each model and serves as an initial comparison of the two models.
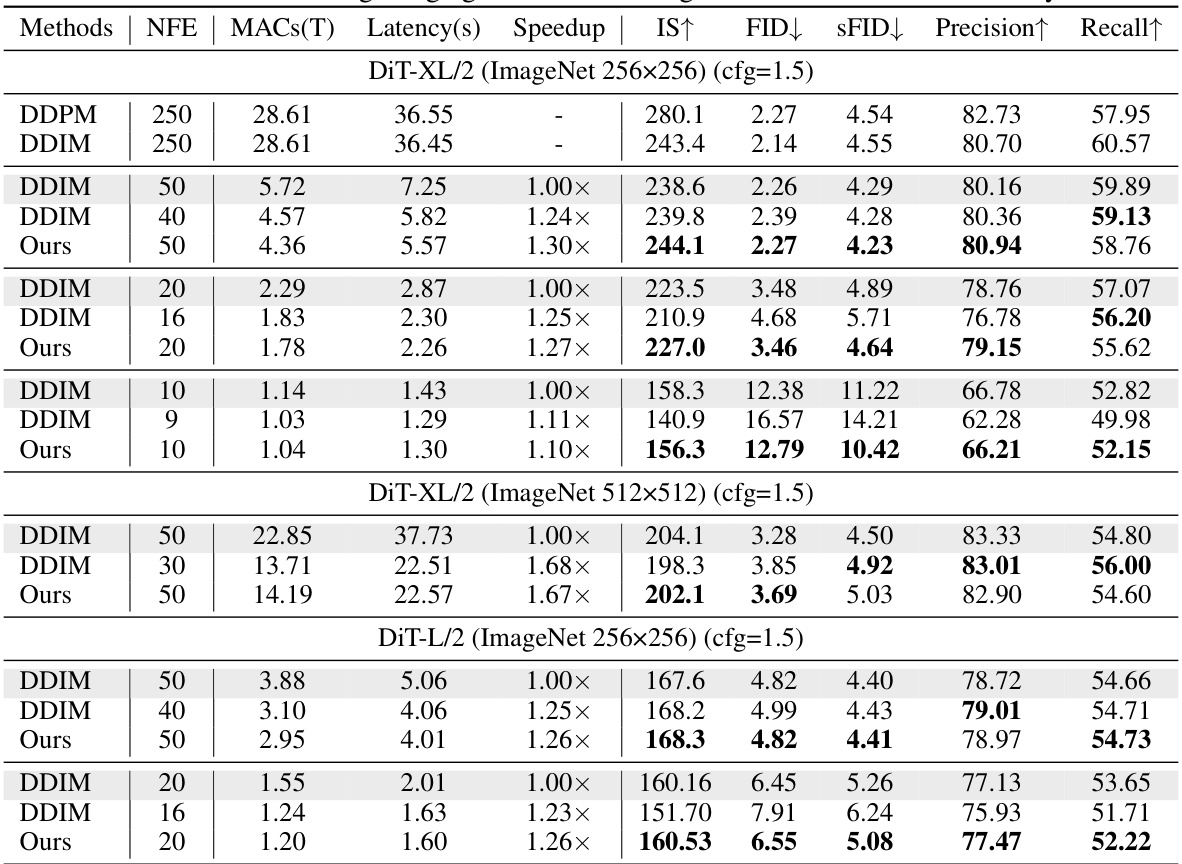
This table presents the results of accelerating image generation on the ImageNet dataset using three different DiT models (DiT-XL/2 256x256, DiT-XL/2 512x512, and DiT-L/2 256x256). The table compares the performance of the proposed Learning-to-Cache (L2C) method against DDIM and shows metrics such as Number of Function Evaluations (NFE), Multiply-Accumulate operations (MACs), latency, speedup, Inception Score (IS), Fréchet Inception Distance (FID), and Recall. The results demonstrate that L2C significantly improves the efficiency of image generation compared to DDIM while maintaining or improving image quality.
In-depth insights#
Diffusion Transformer Speedup#
Accelerating diffusion transformers, known for their high-quality image generation but slow inference, is a crucial area of research. Many approaches focus on reducing the number of sampling steps or model size. This paper explores a novel method: layer caching, identifying redundant computations across timesteps within the transformer architecture. By leveraging the inherent structure of transformers and the sequential nature of diffusion processes, the authors propose a dynamic caching scheme that learns which layers to cache and reuse. A key innovation is the differentiable optimization objective, enabling efficient identification of cacheable layers without an exhaustive search. The proposed ‘Learning-to-Cache’ (L2C) method demonstrates significant speedups with minimal performance degradation, outperforming alternative strategies and achieving high cache hit rates in experiments. The input-invariant, timestep-variant router design is efficient for static computation graph generation, facilitating faster inference. The results highlight the potential of L2C for significantly enhancing diffusion transformer efficiency, particularly for high-resolution image generation.
Learning-to-Cache#
The concept of “Learning-to-Cache” presents a novel approach to accelerating diffusion transformers, a class of models known for their high-quality generative capabilities but slow inference times. The core idea revolves around identifying and exploiting redundant computations across different timesteps in the transformer’s layered architecture. Unlike traditional caching methods, which rely on heuristics or predefined rules for selecting cached layers, this approach uses a differentiable optimization objective to learn an optimal caching strategy. This is achieved by formulating an input-invariant but timestep-variant router that dynamically selects layers to cache and reuse across steps, producing a static computation graph for faster inference. The method’s effectiveness is demonstrated through significant speedups and minimal impact on image quality, achieving considerable improvements over samplers employing fewer steps or other cache-based methods. A key strength is its ability to adapt to different transformer architectures. However, the approach’s reliance on pre-trained models and the inherent constraints on maximum acceleration ratio, potentially due to the caching mechanism implemented, represent limitations for future exploration.
Layer Redundancy#
The concept of ‘Layer Redundancy’ in diffusion models, particularly transformer-based ones, is a crucial yet nuanced area. It explores the potential for computational savings by identifying and removing redundant computations across different layers at the same depth but across various time steps in the diffusion process. This is a key insight because the iterative nature of diffusion models means many steps involve very similar computations. The challenge lies in effectively identifying this redundancy without sacrificing image quality. A naive approach would lead to an exponentially large search space, requiring sophisticated optimization methods. Successful identification of layer redundancy could dramatically improve efficiency, enabling faster and more cost-effective generation of high-quality images. This would greatly impact various applications of diffusion models, especially in real-time or resource-constrained environments. The careful balance between computational optimization and preserving the quality of generated outputs is the core problem addressed by this concept. Techniques such as Learning-to-Cache (L2C) attempt to solve this by learning an optimal caching strategy rather than relying on heuristic rules. The specific implementation and effectiveness of layer redundancy detection and exploitation vary significantly depending on the architecture of the diffusion model. For instance, some architectures might exhibit more redundancy than others.
Cacheable Layer Limits#
The concept of ‘Cacheable Layer Limits’ in a diffusion model research paper is crucial. It investigates the extent to which layers within the transformer architecture can be cached without significantly impacting the model’s performance. This limit is not fixed; it’s dynamic and depends on several factors. The paper likely explores these factors, which may include the specific model architecture (e.g., DiT vs. U-ViT), the image resolution, and the number of denoising steps. Identifying this limit is crucial for optimization, as it helps in designing efficient caching strategies that maximize performance gains without sacrificing image quality. The findings regarding the percentage of cacheable layers (e.g., 93.68% for U-ViT-H/2) likely form a significant part of the paper’s contributions, demonstrating the feasibility and potential of this optimization strategy. Furthermore, the paper likely analyzes the distribution of cacheable layers** within the architecture, possibly revealing architectural patterns that influence layer redundancy and thus cacheability. Investigating this limit provides valuable insights for designing future diffusion models with built-in caching mechanisms for increased efficiency.
Future Research#
Future research directions stemming from this Learning-to-Cache (L2C) method could explore several promising avenues. Extending L2C to other transformer-based diffusion models beyond DiT and U-ViT is crucial to assess its generalizability and effectiveness across different architectures. Investigating the impact of various factors like model size, training data, and hyperparameter settings on the optimal caching strategy would provide a deeper understanding of L2C’s behavior. Developing more sophisticated router architectures that dynamically adjust caching based on input characteristics and timesteps could significantly enhance performance. Furthermore, a theoretical analysis to explain the observed caching patterns and predict the optimal cacheable ratio for various models would be a valuable contribution. Finally, combining L2C with other acceleration techniques, such as parameter-efficient training or quantization, warrants investigation to explore synergistic improvements in inference speed and efficiency. These research directions would strengthen the foundation and broaden the applicability of this promising caching approach.
More visual insights#
More on figures

This figure illustrates the Learning-to-Cache method. It shows how the model dynamically chooses to either perform a full calculation for a layer or reuse the results from a previous step. This choice is controlled by a ‘router’ (β) that smoothly interpolates between performing all computations and using only cached values. The figure highlights that the method operates layer-wise, showing the computation flow through multiple transformer layers (MHSA and Feedforward) and demonstrating the activation/disabling of computations for each layer based on the router’s decision.
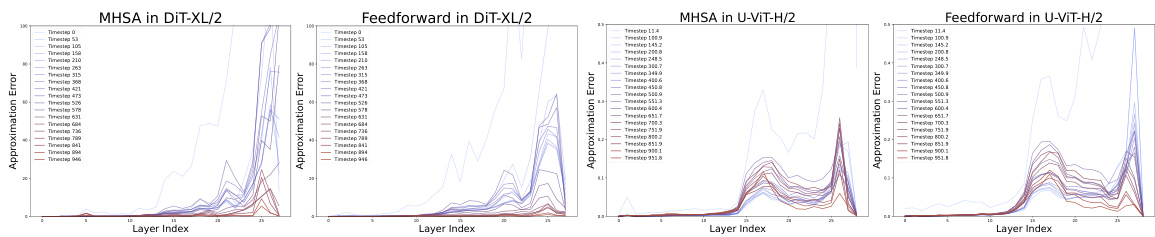
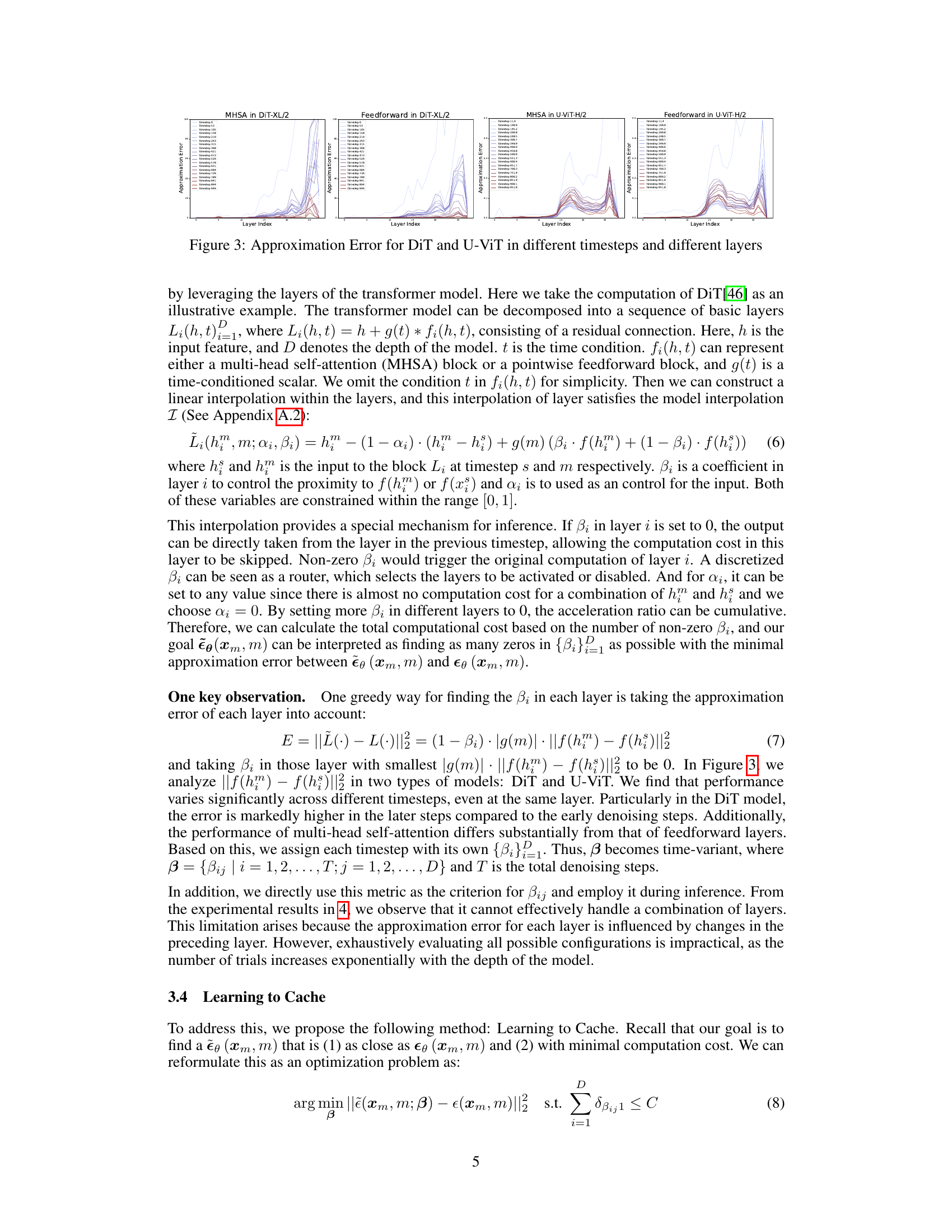
This figure visualizes the approximation error for both DiT and U-ViT models across various timesteps and layers. It illustrates the error in approximating the output of a layer using a cached value from a previous timestep. The plots show the error for both Multi-head Self-Attention (MHSA) and Feedforward layers separately for each model. The x-axis represents the layer index, and the y-axis represents the approximation error. Different colored lines represent different timesteps within the denoising process. The figure is crucial to show the different redundancy patterns in DiT and U-ViT models which motivates the design of the proposed Learning-to-Cache method, as it highlights the varying degrees of error that would result from using cached values.

This figure illustrates the Learning-to-Cache method. It shows how a router (β) dynamically controls whether a layer’s computation is performed (activated) or skipped (disabled) by reusing results from a previous step. This is done to balance speed and accuracy. When a layer is disabled, the non-residual path is bypassed, saving computation time.
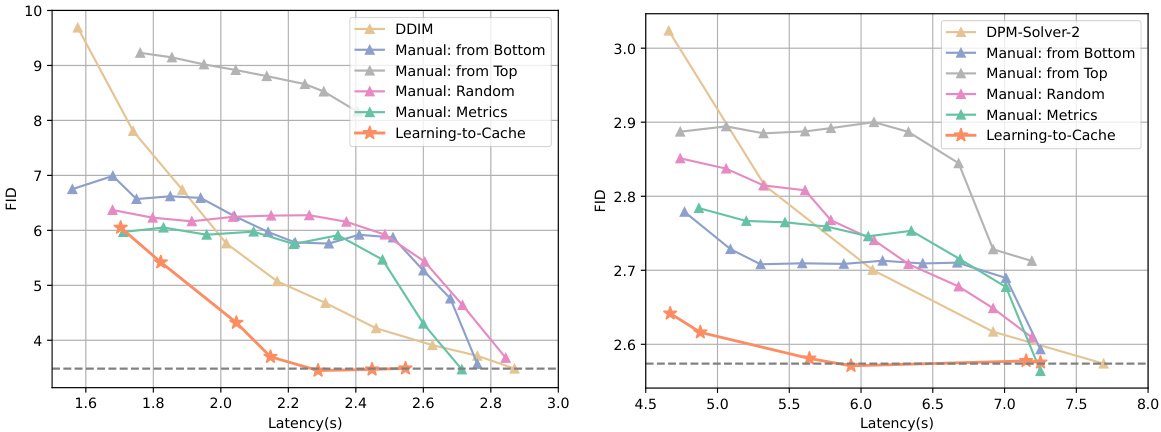
This figure shows the trade-off between FID (Frechet Inception Distance, a metric for image quality) and inference latency for different methods on DiT-XL/2 and U-ViT-H/2 models. The x-axis represents latency (in seconds), and the y-axis represents FID. Lower FID values indicate better image quality, and lower latency values indicate faster inference. Several heuristic methods for selecting layers to cache are compared against the proposed ‘Learning-to-Cache’ method. The dashed line shows the baseline performance without any acceleration techniques. The plot demonstrates that the proposed method achieves a better balance between image quality and inference speed compared to other methods.
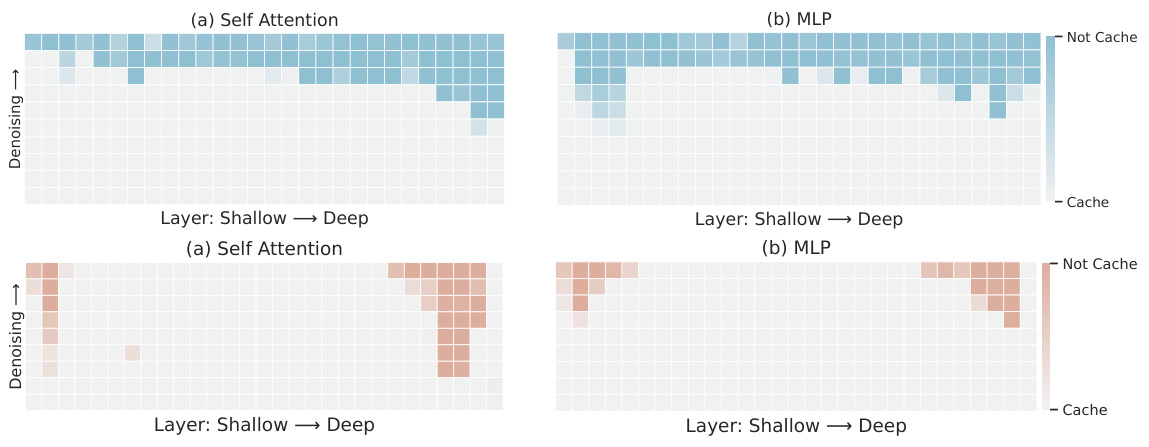
This figure visualizes the learned router beta (β) for two different transformer architectures, DiT-XL/2 and U-ViT-H/2. The heatmaps show the caching patterns learned by the model for each layer across different denoising steps. The lighter colors indicate that the corresponding layer is more likely to be cached (computation skipped), while darker colors mean the layer is less likely to be cached. The figure highlights that different transformer models exhibit distinct caching behaviors, implying that an adaptive caching strategy is necessary for optimal performance across different architectures. The top row shows the learned router for DiT-XL/2, and the bottom row shows the learned router for U-ViT-H/2. The visualization is separated by self-attention (a) and MLP (b) layers.

This figure shows the impact of different threshold values (θ) on the trade-off between image quality (measured by FID) and inference speed (measured by latency). Various threshold values are tested, showing a relationship between the threshold and the speed-quality balance. A higher threshold leads to faster inference but potentially compromises image quality, while a lower threshold gives better quality but slower speed. The optimal choice of threshold depends on the desired balance between speed and quality.

This figure compares the image generation results of four different methods: DDIM, L2C (the proposed method), a method that learns to drop layers, and a method that randomly drops layers. Each method is evaluated using 20 noise-removing steps (NFEs), a measure of computational cost. The top row shows the original images from the ImageNet dataset. The subsequent rows show the generated images from each method, demonstrating the effects of layer caching and dropping techniques on image quality. The caption indicates that the proposed L2C method and the layer-dropping method achieve faster inference than DDIM, but only the proposed L2C method maintain the quality.
More on tables

This table shows the results of experiments using the U-ViT-H/2 model on the ImageNet dataset with a resolution of 256x256. The DPM-Solver-2 sampling method was used, which performs two function evaluations per step. The table compares different numbers of function evaluations (NFEs) for the baseline DPM-Solver and the proposed Learning-to-Cache (L2C) method, reporting metrics such as MACs (multiply-accumulate operations), latency, speedup, and FID (Fréchet Inception Distance). Guidance strength was set to 0.4.
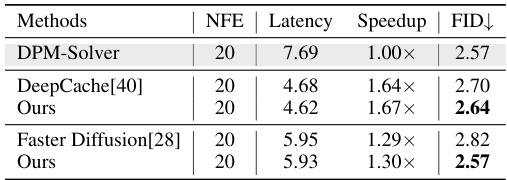
This table compares the proposed Learning-to-Cache method with other cache-based methods (DeepCache and Faster Diffusion) on the U-ViT model. It shows the number of function evaluations (NFE), latency, speedup relative to DPM-Solver, and FID (Fréchet Inception Distance) for each method. Lower FID indicates better image quality, and higher speedup indicates faster inference.
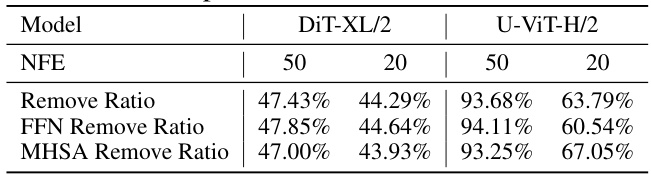
This table shows the maximum percentage of layers that can be cached in DiT-XL/2 and U-ViT-H/2 models without significantly impacting image quality, for different numbers of sampling steps (NFE). It breaks down the cacheable layers into feed-forward (FFN) and multi-head self-attention (MHSA) layers separately. The high percentage of cacheable layers, especially in U-ViT-H/2, demonstrates the effectiveness of the proposed Learning-to-Cache (L2C) method in identifying redundant computations across timesteps.

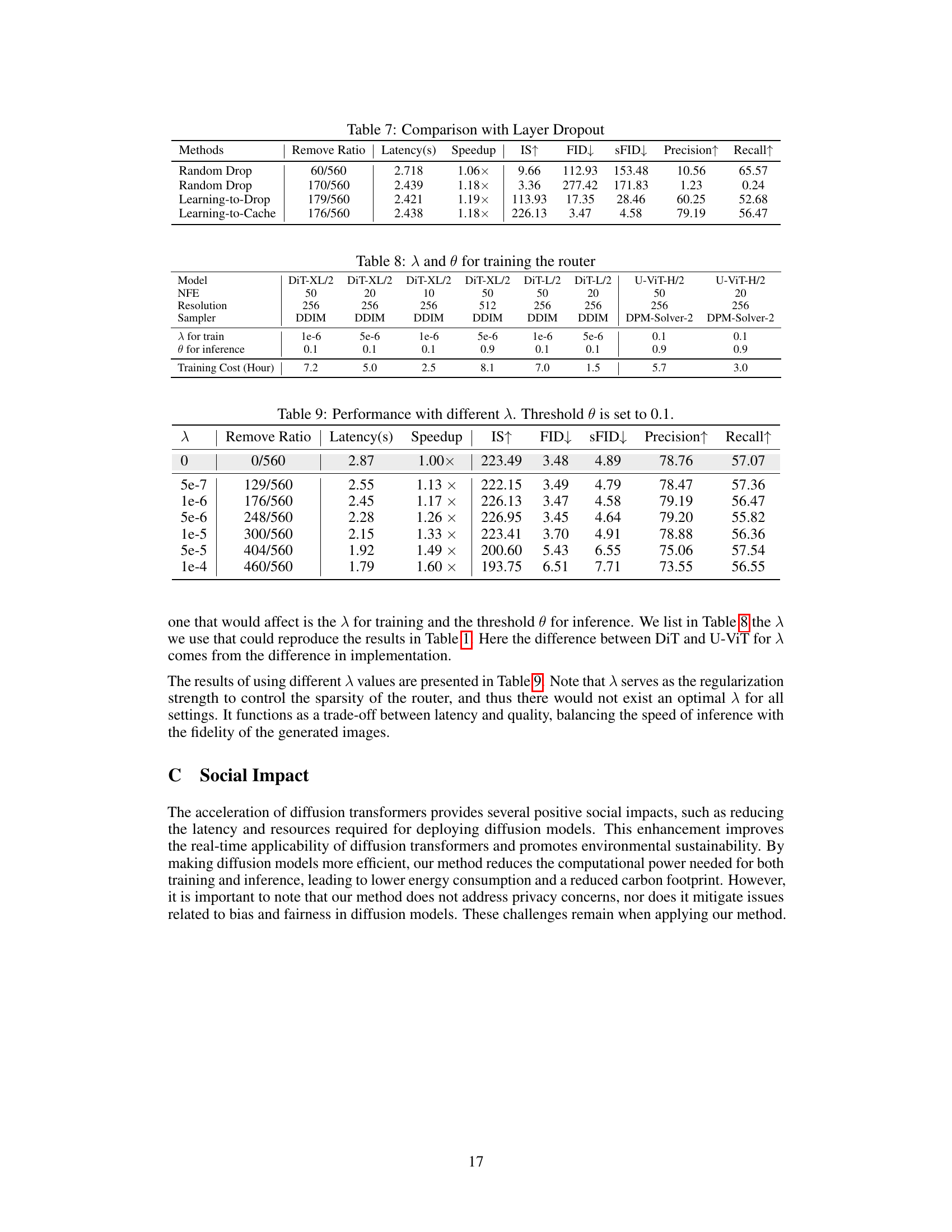
This table compares the performance of three different methods for accelerating diffusion transformers on the U-ViT model: Random Drop, Learning-to-Drop, and Learning-to-Cache. The methods are evaluated based on the number of layers removed, latency, speedup factor, Inception Score (IS), Frechet Inception Distance (FID), sFID, precision, and recall. The results demonstrate that the Learning-to-Cache method outperforms the other two methods across various metrics, showcasing its effectiveness in improving the speed and performance of diffusion transformer models without significant loss of image quality.

This table compares the performance of DPM-Solver with and without shifted cache steps. The ‘Cache’ row shows results when caching is applied, and the ‘Cache - shifted’ row demonstrates the impact of shifting the cache steps to improve derivative accuracy. Note that all layers are cached in both scenarios. The metrics evaluated are NFE (number of function evaluations), latency (in seconds), speedup (relative to the base DPM-Solver), Inception Score (IS), Frechet Inception Distance (FID), sFID, Precision, and Recall.

This table compares the performance of Learning-to-Cache with other layer dropout methods on the U-ViT model. It shows the latency, speedup, Inception Score (IS), Frechet Inception Distance (FID), and other metrics for different methods with varying layer removal ratios.

This table shows the hyperparameters λ and θ used for training the router in different model configurations. λ is a regularization parameter controlling the sparsity of the router, and θ is a threshold used during inference to discretize the router’s output. The table specifies these values for various diffusion transformer models (DiT-XL/2, DiT-L/2, U-ViT-H/2) with varying numbers of function evaluations (NFEs) and resolutions. The training cost in hours is also listed for each configuration.
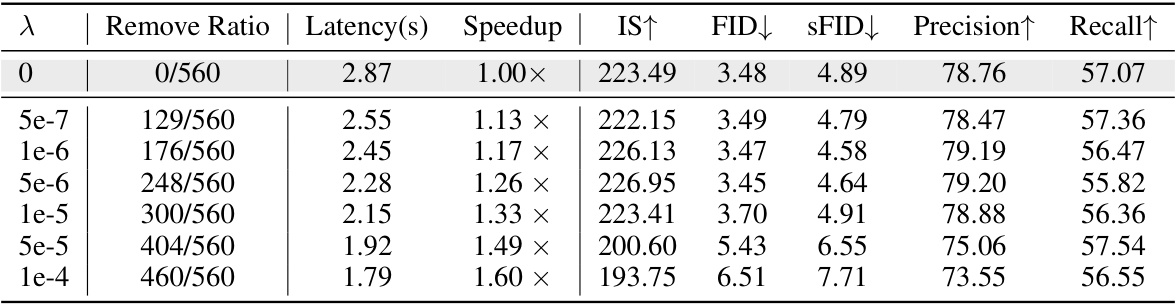
This table shows the impact of the hyperparameter λ on the performance of the Learning-to-Cache method. Different values of λ lead to varying numbers of cached layers (Remove Ratio), resulting in different inference latencies, speedups, and image quality metrics (IS, FID, sFID, Precision, Recall). The threshold θ, which determines whether a layer is cached or not, is fixed at 0.1 for all experiments in this table. Lower λ values result in fewer layers being cached and slower inference but potentially better image quality.
Full paper#