A Separation in Heavy-Tailed Sampling: Gaussian vs. Stable Oracles for Proximal Samplers

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial for researchers working on heavy-tailed sampling because it identifies a fundamental limitation of Gaussian-based samplers and introduces a novel high-accuracy approach using stable oracles. This opens new avenues for improving the efficiency and effectiveness of Bayesian statistics, machine learning, and other fields dealing with heavy-tailed data. The separation result is a significant contribution to the theoretical understanding of sampling algorithms.

Visual Insights

#

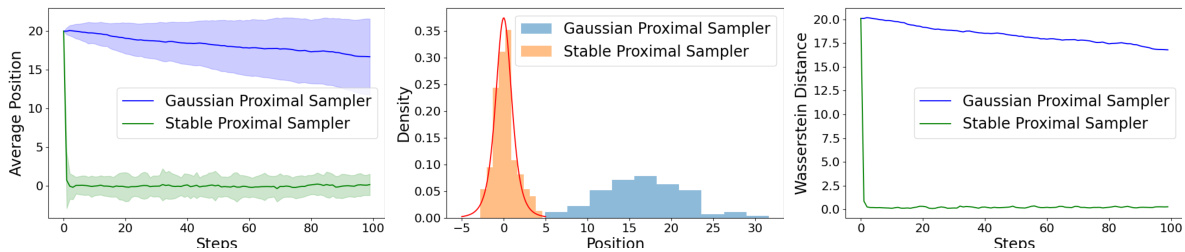
This figure compares the performance of Gaussian and Stable Proximal Samplers in sampling from a one-dimensional Student-t distribution with 4 degrees of freedom. The left panel shows the average position of the samples over 100 independent runs, with shaded regions representing the standard deviation. The middle panel displays histograms of the final sample positions from both samplers, overlaid with the target density. The right panel illustrates the Wasserstein-2 distance between the sample distribution and the target distribution at each iteration. The initial sample position is set to 20. The figure highlights the superior convergence properties of the stable sampler compared to the Gaussian sampler in this heavy-tailed scenario.

This table summarizes the upper and lower complexity bounds for generating an ɛ-accurate sample using proximal samplers with Gaussian vs. stable oracles. The target distribution is a generalized Cauchy distribution with varying degrees of freedom (ν). The table shows a separation in complexity between the Gaussian and stable oracles, highlighting the superior performance of stable oracles, especially for heavy-tailed distributions (ν ∈ (0,1)). The complexity is measured in terms of the number of iterations needed to achieve ɛ-accuracy, expressed using Big O notation.

In-depth insights

#

Heavy-tailed Sampling

#

Heavy-tailed sampling presents a unique challenge in statistical computing due to the slow decay of probability density functions in the tails. Traditional MCMC methods often struggle in these scenarios because of diminishing gradients, leading to slow convergence rates. This paper explores the use of proximal samplers with different oracles—Gaussian and stable—to address this. A key finding is the separation in performance: Gaussian oracles show limitations in achieving high-accuracy guarantees for heavy-tailed distributions, while stable oracles demonstrate superior performance. This highlights the importance of choosing appropriate sampling methods based on the target distribution’s tail behavior. The theoretical analysis provides complexity bounds, establishing that stable oracles offer significantly improved sampling efficiency. The study motivates the development and use of stable-driven stochastic differential equations as a more effective approach for heavy-tailed sampling. The paper also discusses implementation details and lower bounds, demonstrating the optimality of the proposed algorithms.

Gaussian Oracle Limits

#

The heading ‘Gaussian Oracle Limits’ likely discusses limitations of using Gaussian distributions as proposal mechanisms within Markov Chain Monte Carlo (MCMC) algorithms, particularly in the context of heavy-tailed target distributions. The core idea revolves around the fact that Gaussian proposals struggle to efficiently explore the extreme regions of heavy-tailed distributions, which often contain significant probability mass. This limitation translates to slow convergence rates and inefficient sampling. The section likely presents theoretical arguments demonstrating this inefficiency, possibly through lower bounds on the mixing time or convergence rate for specific heavy-tailed distributions when using Gaussian oracles. These theoretical results might highlight a fundamental barrier for Gaussian-based methods in high-dimensional heavy-tailed sampling, motivating the exploration of alternative proposal mechanisms (e.g., stable distributions) which better adapt to the target distribution’s tails. The analysis may involve a detailed study of the Langevin diffusion and the proximal sampler, showing that their performance deteriorates polynomially with respect to accuracy requirements when the target is heavy-tailed. In summary, this section establishes a separation result highlighting the superiority of alternative oracles, such as stable oracles, over Gaussian oracles for sampling from heavy-tailed target distributions.

Stable Oracle Benefits

#

The concept of a “Stable Oracle” within the context of heavy-tailed sampling offers significant advantages over traditional Gaussian oracles. Stable oracles, by leveraging stable distributions, directly address the challenges posed by slowly decaying tails in target densities. Unlike Gaussian oracles that struggle with diminishing gradients, stable oracles enable more efficient high-accuracy sampling techniques with computational complexity scaling logarithmically rather than polynomially with the desired accuracy. This is a crucial improvement, overcoming a fundamental barrier inherent in Gaussian-based proximal samplers. The use of fractional heat flows, inherently tied to stable processes, provides a powerful theoretical framework for understanding and improving the performance of these samplers. While the implementation of stable oracles might involve challenges like exact simulation, recent advancements suggest practical solutions such as rejection sampling to achieve similar high-accuracy guarantees. The separation in performance between Gaussian and stable oracles highlights the importance of selecting the appropriate oracle based on the characteristics of the target distribution. Further research could focus on developing more efficient algorithms and broadening the applicability of stable oracles to a wider range of heavy-tailed problems.

Algorithm Complexity

#

The algorithm complexity analysis in this research paper is a crucial aspect, focusing primarily on the comparison of Gaussian and stable oracles within proximal samplers for heavy-tailed target distributions. The core finding highlights a separation in achievable accuracy: Gaussian oracles exhibit a fundamental barrier, only offering low-accuracy guarantees (poly(1/ε) iterations), while stable oracles enable high-accuracy guarantees (O(log(1/ε)) iterations). This separation is rigorously demonstrated through upper and lower bounds on iteration complexity for both oracle types, showcasing the superior performance of stable oracles in overcoming inherent limitations with heavy-tailed sampling. The analysis also delves into the practical implications, presenting and analyzing a stable proximal sampler with an easily implementable a-stable oracle (a=1), demonstrating its effectiveness in various heavy-tailed scenarios. This detailed complexity analysis reveals a significant advance in the field, offering both theoretical understanding and practical guidance for selecting appropriate sampling methods based on desired accuracy and target distribution characteristics.

Future Research

#

The paper’s ‘Future Research’ section would ideally explore several promising avenues. Extending the stable proximal sampler to handle a wider range of heavy-tailed distributions beyond the generalized Cauchy class is crucial. This involves investigating the applicability of fractional Poincaré inequalities or alternative functional inequalities for characterizing the tails of more complex heavy-tailed distributions. Improving the efficiency of the proposed stable oracle is another important direction, possibly through developing more efficient rejection sampling techniques or exploring alternative numerical methods for generating samples from stable distributions. A thorough comparative analysis of the stable proximal sampler against other state-of-the-art heavy-tailed samplers is needed, using diverse real-world datasets to assess performance in practical settings. This should also encompass detailed analysis of scalability and robustness to noise in the context of high-dimensional problems. Finally, investigating the theoretical implications of the stable sampler’s connection to fractional heat flows and their relationships to gradient flow methods would enrich our understanding of its underlying mechanisms, potentially leading to further algorithmic improvements and insights.

More visual insights

#

More on figures

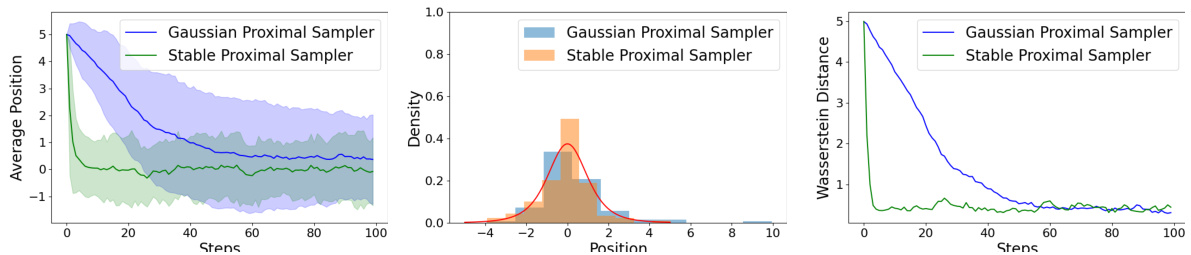
This figure compares the performance of Gaussian and Stable Proximal Samplers in sampling from a one-dimensional student-t distribution with 4 degrees of freedom. The left panel shows the average position of samples over 100 independent runs, illustrating the faster convergence of the Stable sampler. The center panel displays histograms of the final sample positions for both methods alongside the true target density, visually demonstrating the Stable sampler’s superior accuracy. The right panel plots the Wasserstein distance between the empirical distribution of samples and the true distribution, again showcasing the Stable sampler’s faster convergence to the target distribution.

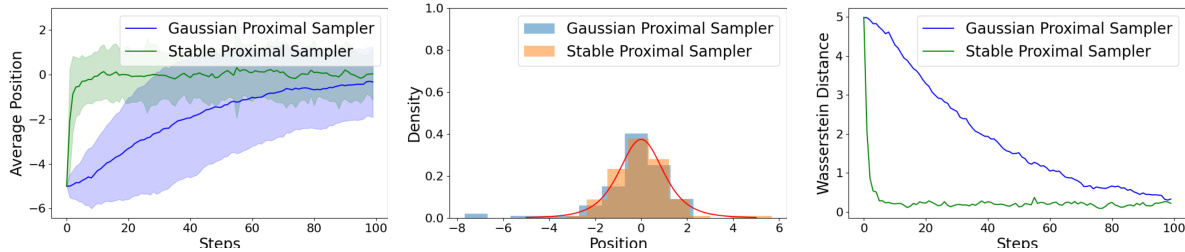
This figure compares the performance of Gaussian and Stable Proximal Samplers in sampling from a one-dimensional student-t distribution with 4 degrees of freedom. The left panel shows the average position of samples over time (steps), illustrating the convergence towards the target distribution’s mean (0). The shaded regions represent the variance or uncertainty in the sample mean. The center panel displays histograms of the final sample positions generated by both samplers, along with the true student-t density (red curve), visually demonstrating the accuracy of the sampling. The right panel shows the Wasserstein distance, a measure of similarity between the generated sample distribution and the target distribution, over time. This distance decreases as the samplers converge towards the target.

This figure compares the performance of Gaussian and Stable Proximal Samplers in sampling from a one-dimensional Student’s t-distribution. The left panel shows the average position of the samples over time, with shaded regions representing the standard deviation. The middle panel displays the histograms of the final sample distributions generated by each method, compared to the target distribution (in red). The right panel illustrates the convergence of the Wasserstein-2 distance between the generated and target distributions over time. The initial point for sampling is x0=20.

More on tables

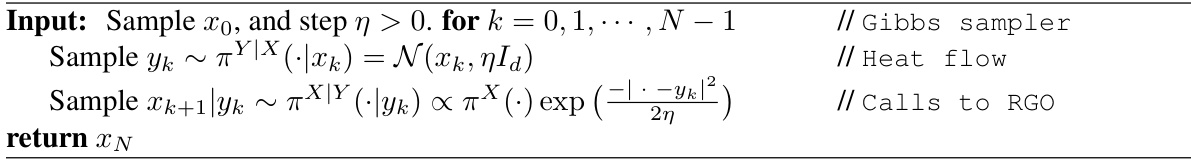
This table summarizes the upper and lower bounds on the iteration complexity for proximal samplers using Gaussian and stable oracles to generate an ɛ-accurate sample from generalized Cauchy distributions. It highlights a separation result, showing that Gaussian oracles only achieve low-accuracy guarantees (polynomial dependence on 1/ɛ), while stable oracles achieve high-accuracy guarantees (logarithmic dependence on 1/ɛ) for certain parameter ranges. The complexity is measured in terms of χ²-divergence.

This table summarizes the upper and lower complexity bounds for generating an Ɛ-accurate sample using proximal samplers with Gaussian and stable oracles. The target distribution is a generalized Cauchy distribution with varying degrees of freedom (ν). The table highlights a separation in complexity between Gaussian and stable oracles, showing that stable oracles can achieve significantly lower complexity (O(log(1/Ɛ)) in some cases) compared to Gaussian oracles (poly(1/Ɛ)) for heavy-tailed sampling.

This table compares the upper and lower bounds on the iteration complexity of proximal samplers using Gaussian vs. Stable oracles to obtain an ε-accurate sample from a generalized Cauchy distribution. The complexity is measured in terms of the chi-squared divergence. The table shows that Stable oracles achieve significantly better complexity (O(log(1/ε))) than Gaussian oracles, especially for heavy-tailed distributions (small v).

Full paper

#