↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Gaussian Mixture Models (GMMs) are fundamental in machine learning for clustering and density estimation, but learning them using the popular Expectation-Maximization (EM) algorithm faces challenges, especially in over-parameterized settings (more model parameters than data support). Previous work has shown limited results, mostly for simple 2-component mixtures and often lacking global convergence guarantees. The non-monotonic convergence behavior adds further difficulty in the theoretical analysis.
This paper makes a significant breakthrough by rigorously proving the global convergence of gradient EM for over-parameterized GMMs, achieving the first such result for more than 2 components. They achieve this using a novel likelihood-based convergence analysis framework. The method provides a sublinear convergence rate, a finding explained by the inherent algorithmic properties of the model. Moreover, the research highlights a new challenge: the existence of bad local minima that can trap the algorithm for exponentially long periods, influencing future research in algorithm design.
Key Takeaways#
Why does it matter?#
This paper is crucial because it solves a long-standing open problem in machine learning: proving the global convergence of gradient Expectation-Maximization (EM) for Gaussian Mixture Models (GMMs). This is important for developing robust and reliable algorithms for clustering and density estimation, impacting various applications in data analysis and AI. The discovery of bad local regions that trap gradient EM is also significant, providing valuable insights for future algorithm development and theoretical analysis.
Visual Insights#
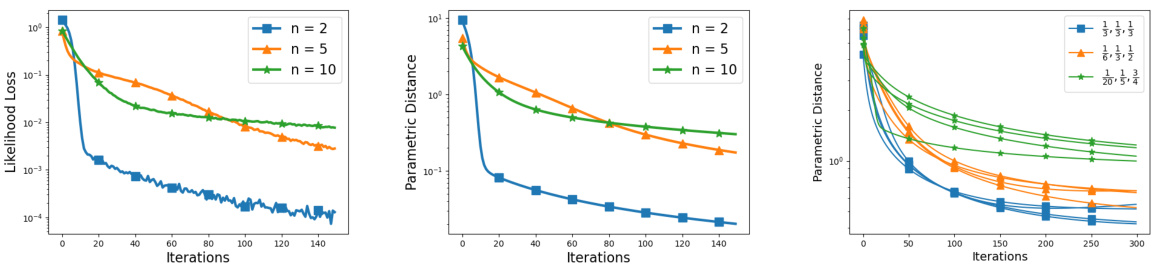
This figure demonstrates the sublinear convergence of gradient EM for over-parameterized Gaussian Mixture Models (GMMs). The left panel shows the sublinear decrease in likelihood loss (L) over iterations for models with 2, 5, and 10 components. The middle panel displays the sublinear convergence of the parametric distance between the learned model and the ground truth, which is a single Gaussian. The right panel illustrates how different mixing weights in the GMM affect the convergence speed.
Full paper#



















