↗ OpenReview ↗ NeurIPS Homepage ↗ Hugging Face ↗ Chat
TL;DR#
Deploying large language models (LLMs) is challenging due to their high computational and memory costs. Existing quantization methods, aimed at reducing these costs, struggle with severe performance degradation when bit-widths are extremely low. This is mainly due to drastic precision loss at extremely low-bit weight representation, impacting the linear projection, a crucial operation in LLMs.
To overcome these limitations, the paper introduces OneBit, a novel 1-bit model compressing framework. OneBit utilizes a novel 1-bit parameter representation to better quantize LLMs and incorporates an effective parameter initialization method. Experimental results on multiple LLMs demonstrate that OneBit achieves robust training processes and good performance (at least 81% of non-quantized performance) using only 1-bit weight matrices, outperforming previous 2-bit baselines. This significantly advances extremely low-bit LLM deployment.
Key Takeaways#
Why does it matter?#
This paper is important because it significantly advances the field of model compression, addressing the limitations of existing methods and demonstrating the feasibility of extremely low-bit quantization for large language models. It opens new avenues for deploying LLMs on resource-constrained devices, making them more accessible and applicable in various settings, and also provides valuable insights into the training and optimization techniques for extremely low-bit models. The proposed method and findings will be highly influential in future research, shaping the development of more efficient and versatile LLMs.
Visual Insights#
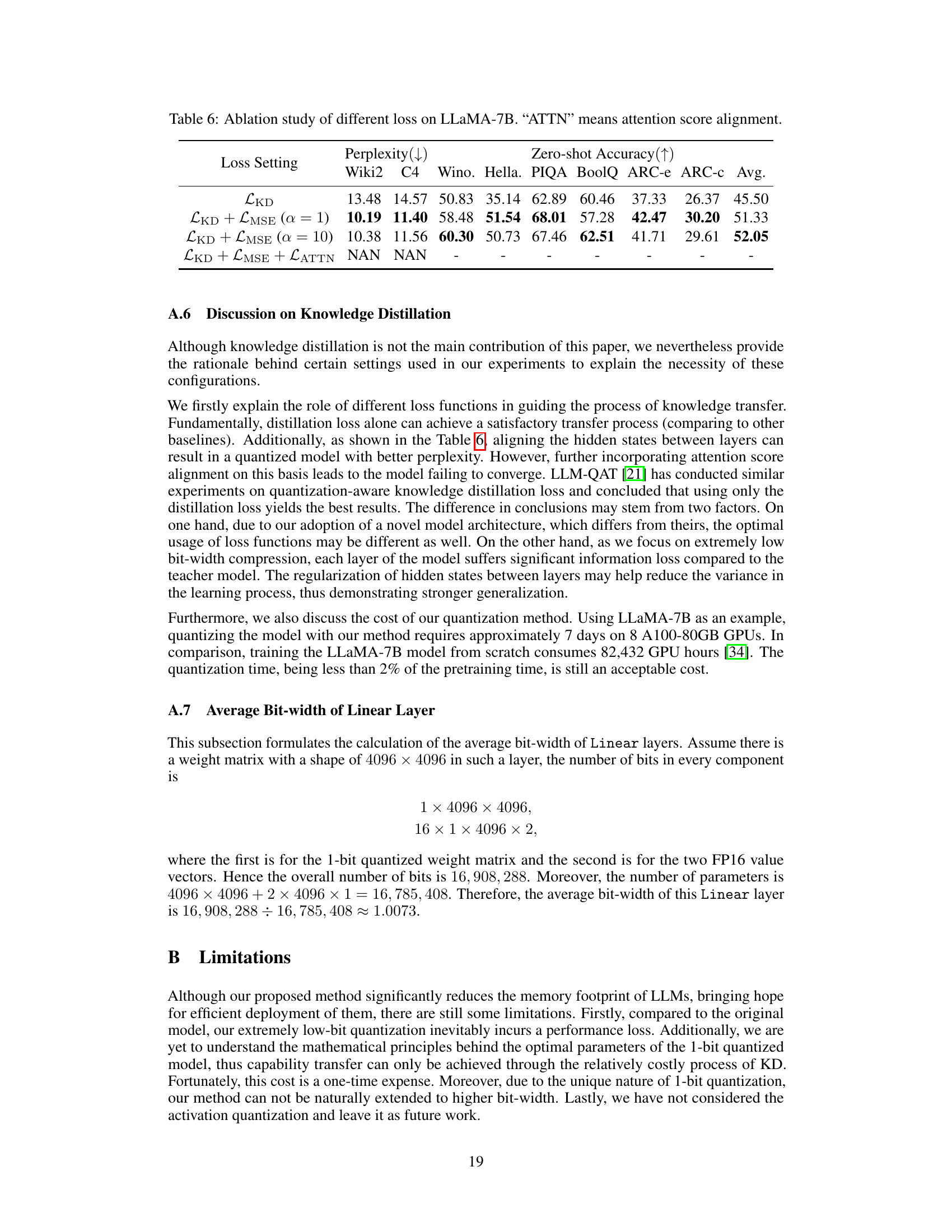
This figure compares the perplexity achieved by several existing low-bit quantization methods (GPTQ, LLM-QAT, OmniQuant) against the proposed OneBit method on the LLaMA-7B model. The x-axis represents the number of bits used for weight quantization, and the y-axis shows the resulting perplexity on the Wikitext2 benchmark. The graph highlights that the performance of existing methods significantly degrades as the bit-width decreases below 4 bits. In contrast, the OneBit method demonstrates superior performance, even when using only 1 bit for weight quantization.

This table presents the hyperparameters used for training the models in the knowledge distillation experiments. Specifically, it lists the learning rate, alpha (α) value which balances the loss functions, and the number of GPUs utilized for each model size (OPT-1.3B, OPT-2.7B, LLaMA-7B, LLaMA-13B, LLaMA2-7B, LLaMA2-13B).
In-depth insights#
1-bit LLM Quantization#
1-bit LLM quantization is a significant advancement in model compression, aiming to drastically reduce the memory footprint and computational cost of large language models (LLMs). The core challenge lies in mitigating the substantial performance degradation typically associated with extremely low-bit quantization. Existing methods struggle below 2-bits, highlighting the difficulty of maintaining accuracy with such limited precision. Novel techniques, such as the proposed Sign-Value-Independent Decomposition (SVID), are necessary to effectively represent the weight matrices in a 1-bit format. SVID mathematically separates the weight matrix into a sign matrix and value vectors, preserving crucial information while minimizing storage. Knowledge distillation plays a key role in transferring the capabilities of the original high-precision model to the 1-bit quantized version, ensuring reasonable performance. Robust training procedures are crucial to ensure the stability of the compressed model. While the approach yields impressive compression ratios, careful consideration must be given to its limitations and the tradeoffs between accuracy, memory savings, and computational speed.
SVID Parameter Init#
The effectiveness of 1-bit quantization hinges critically on proper parameter initialization. The proposed Sign-Value-Independent Decomposition (SVID) method directly addresses this challenge. SVID mathematically decomposes high-bit weight matrices into a low-bit sign matrix and two value vectors, enabling efficient 1-bit representation while retaining crucial information. This approach is superior to naive rounding methods which suffer significant information loss at such low bit-widths. The decomposition facilitates a smooth transition between high-precision and low-precision weight representations, improving model convergence speed and overall performance. The choice of decomposition technique (e.g., SVD or NMF) may impact performance, as the selection of the appropriate method can further enhance the effectiveness of initialization for training stability. Importantly, this method leverages the already-trained high-precision weights; thus, it requires no additional training data in its process, unlike other methods. The impact of SVID is shown through experimental results exhibiting improved performance and convergence.
KD Knowledge Transfer#
Knowledge distillation (KD) is a crucial technique in the paper for effectively transferring knowledge from a larger, higher-precision model (teacher) to a smaller, lower-precision model (student). This is particularly important because the student model, quantized to 1-bit, suffers from a significant loss of precision. KD helps mitigate this loss by guiding the student’s learning process with information derived from the teacher. The method uses both cross-entropy loss on logits and mean-squared-error loss on hidden states to ensure both output and representation consistency between teacher and student models. The careful balancing of these losses is critical for successful knowledge transfer and optimal performance. The process ensures the compressed student model retains the essential capabilities of the original model, despite its drastic reduction in parameters. In essence, KD acts as a bridge, transferring the knowledge accumulated by the teacher to the resource-efficient student, addressing the limitations imposed by extreme quantization and ensuring robust training despite the challenge of working with 1-bit weights.
Performance Analysis#
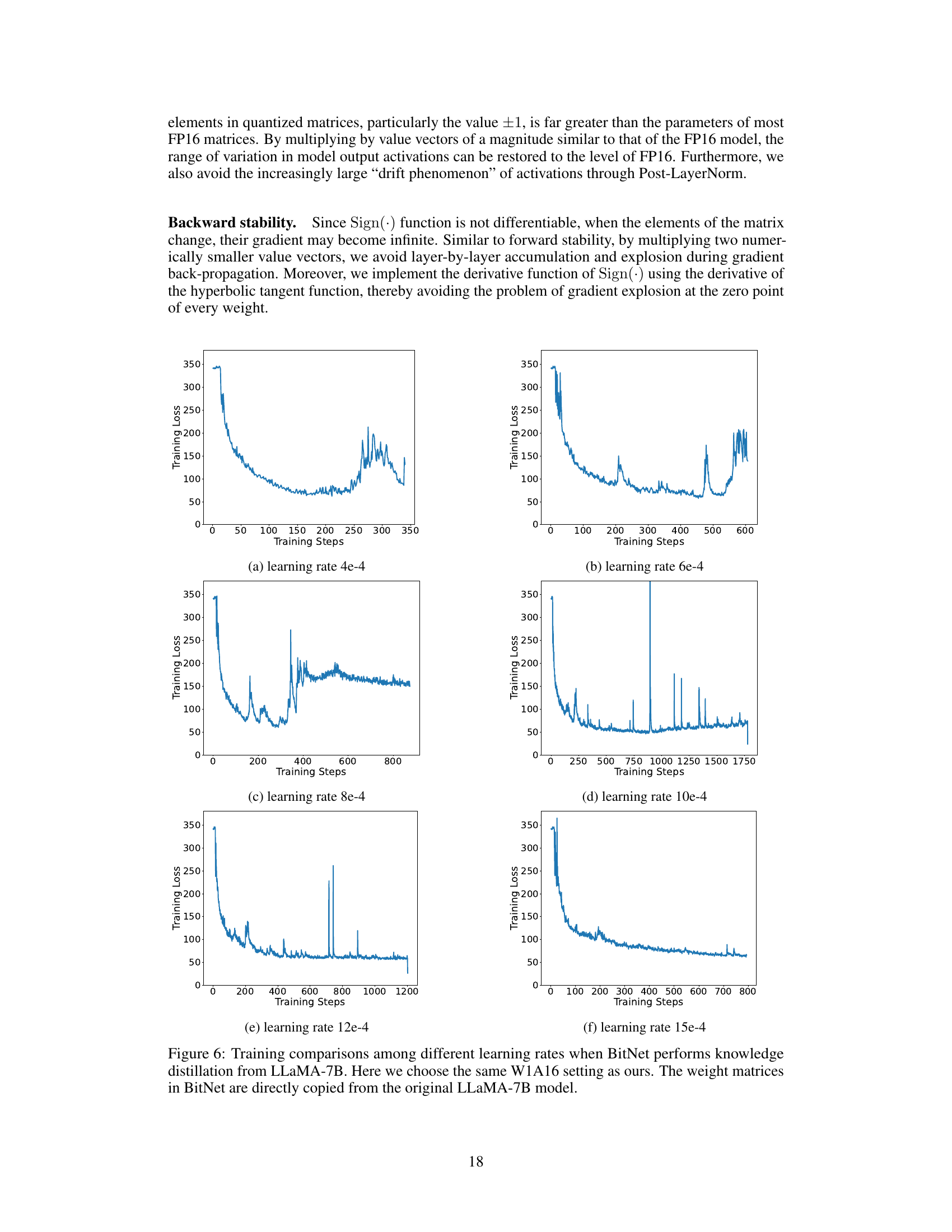
A thorough performance analysis of any low-bit large language model (LLM) quantization method would necessitate a multi-faceted approach. Key metrics would include perplexity scores on benchmark datasets like WikiText2 and C4, assessing the model’s ability to predict the next word in a sequence. Zero-shot performance on various downstream tasks (e.g., question answering, commonsense reasoning) would reveal the model’s generalized capabilities after quantization. Computational efficiency should be evaluated, comparing inference speed and memory footprint of the quantized model against its full-precision counterpart. Crucially, the robustness of the training process needs examination; the analysis should explore how sensitive the quantized model is to hyperparameter choices and the impact of variations in training data. A comparison to state-of-the-art low-bit quantization methods is vital to gauge the proposed method’s effectiveness. Finally, analysis of the trade-offs between compression ratio, accuracy, and inference speed is essential. A comprehensive performance analysis will provide significant insights into the method’s practical viability.
Future Work#
Future research directions stemming from this 1-bit quantization method for LLMs could explore several promising avenues. Extending the approach to handle activation quantization alongside weight quantization could further improve compression ratios and potentially enhance model performance. Investigating alternative decomposition methods beyond SVID, such as exploring lower-rank approximations or other matrix factorization techniques, might lead to improved initialization strategies and faster training convergence. A deeper investigation into the robustness of the method to different model architectures and datasets is crucial to establish its generalizability. This includes evaluating its effectiveness on various LLM sizes and types beyond those tested, and determining how sensitive it is to variations in training data and hyperparameters. Finally, developing techniques to mitigate the inherent instability challenges associated with extremely low-bit quantization will be vital for broader adoption. This might involve novel training methods, regularization techniques, or hardware-aware optimizations.
More visual insights#
More on figures

This figure illustrates the core idea behind the OneBit model’s 1-bit linear layer. The left panel shows a standard FP16 linear layer, where both the input activation (X) and the weight matrix (W) are in FP16 format. The right panel depicts the proposed OneBit architecture. Here, the weight matrix is quantized to 1-bit (represented as ±1), significantly reducing the memory footprint. To compensate for the information loss due to this extreme quantization, two value vectors (g and h), which maintain FP16 precision, are introduced. These vectors help preserve the necessary floating-point precision during the linear transformation while keeping the weights themselves extremely low-bit.

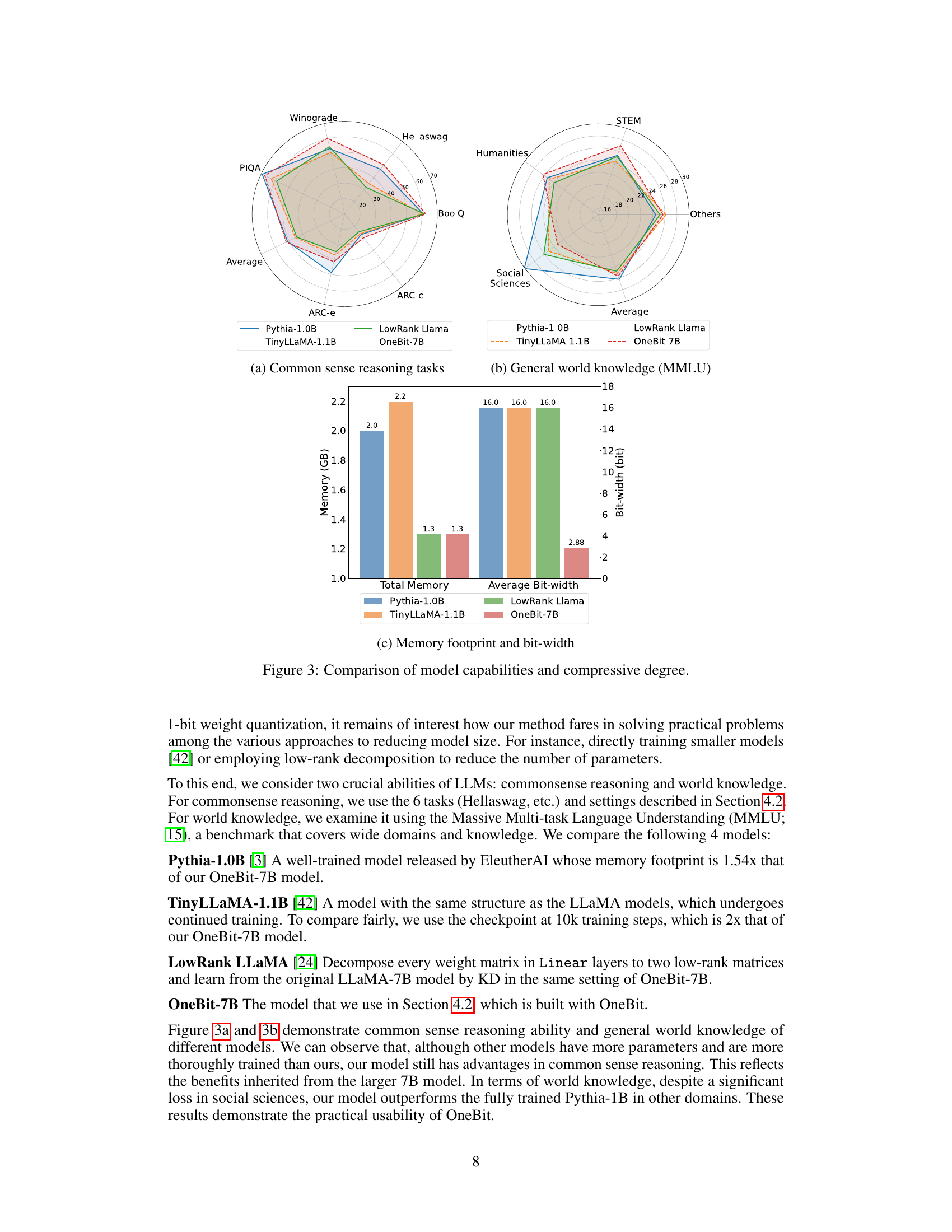
This figure compares four different language models in terms of their performance on common sense reasoning tasks and general world knowledge tasks. The models compared are Pythia-1.0B, TinyLLaMA-1.1B, LowRank LLaMA, and OneBit-7B. The figure shows that OneBit-7B, despite having a much smaller memory footprint and lower average bit-width, performs comparably to the other models on many tasks, particularly commonsense reasoning. This demonstrates the effectiveness of the OneBit quantization technique in compressing large language models while maintaining their performance.
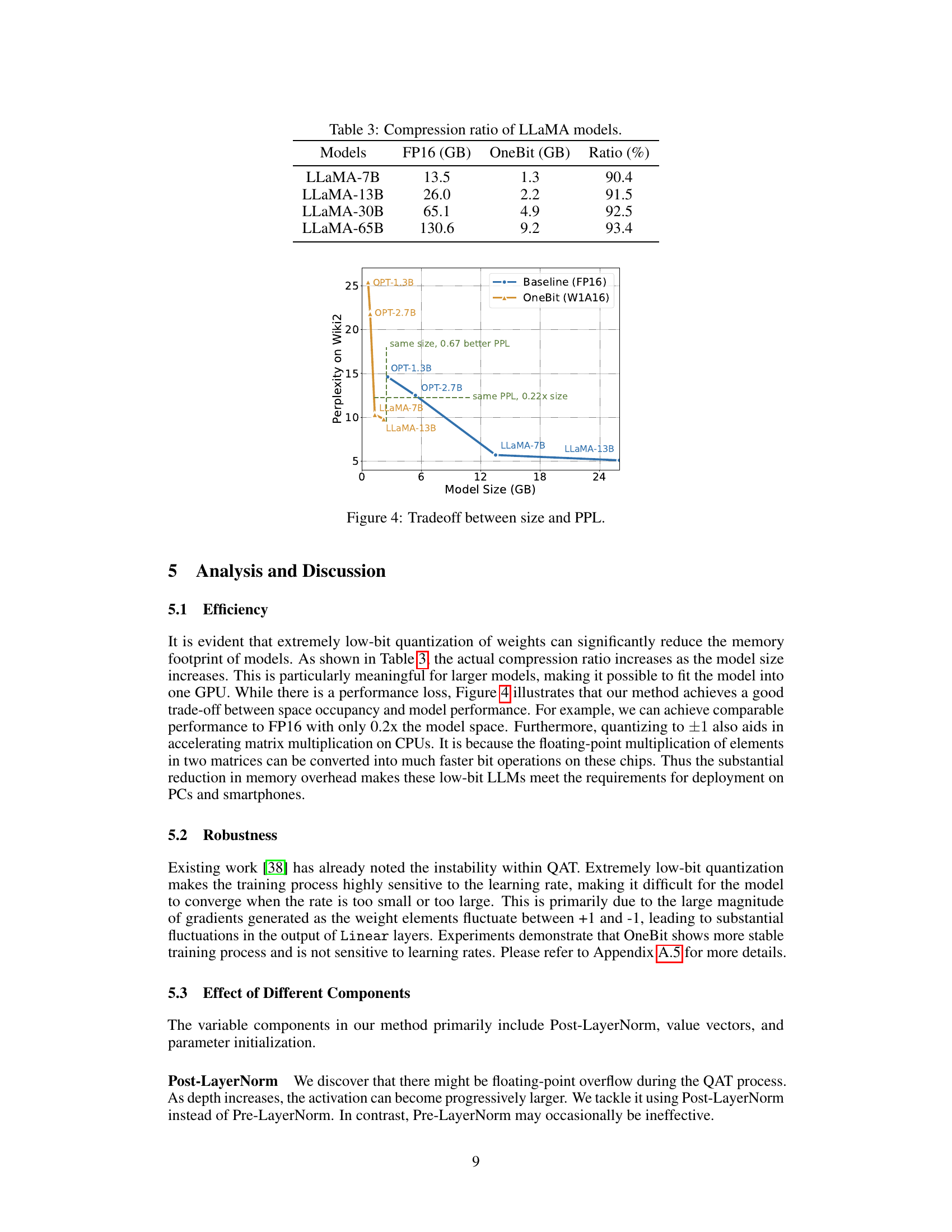
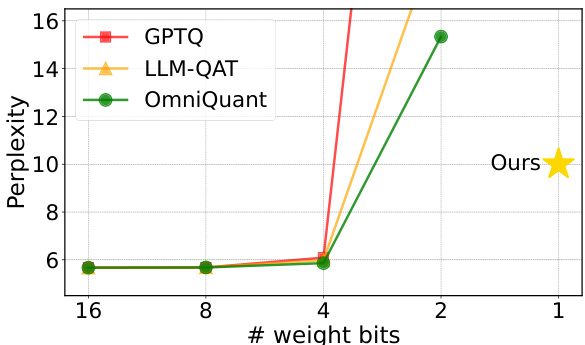
This figure shows the trade-off between model size and perplexity (PPL) for different models. The x-axis represents the model size in GB, and the y-axis represents the perplexity on the Wiki2 dataset. The blue line represents the baseline performance using FP16 precision, while the orange line shows the performance of the OneBit method using 1-bit weights and 16-bit activations (W1A16). The figure highlights that OneBit achieves comparable performance to the FP16 baseline with significantly reduced model sizes. For example, it achieves similar perplexity to OPT-2.7B at only 0.22x the model size. Conversely, it shows improved perplexity over the baseline at the same model size for OPT-1.3B and OPT-2.7B.

This figure shows the training loss curves for different methods of initializing the 1-bit weight matrix in the OneBit-7B model. Three methods are compared: Singular Value Decomposition (SVD), Non-negative Matrix Factorization (NMF), and simply copying from the original weight matrix. The plot shows that NMF converges faster and reaches a lower training loss compared to SVD and copying from the original weights. This illustrates the effectiveness of the SVID-based initialization method proposed in the paper.

This figure compares four different models (Pythia-1.0B, TinyLLaMA-1.1B, LowRank LLAMA, and OneBit-7B) across various metrics. Subfigure (a) shows performance on common sense reasoning tasks. Subfigure (b) shows performance on general world knowledge tasks (MMLU). Subfigure (c) provides a comparison of memory footprint and the average bit-width used in each model. The figure demonstrates that the OneBit model, despite having a significantly smaller memory footprint and lower bit-width, achieves comparable performance to other models, particularly in common sense reasoning.
More on tables
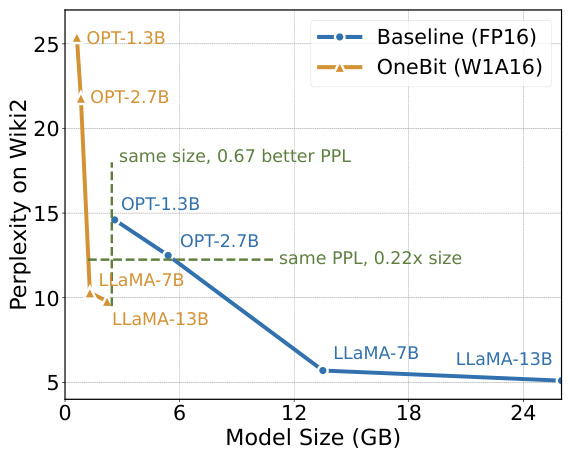
This table presents the main experimental results, comparing the performance of OneBit against other state-of-the-art quantization methods across multiple LLMs (OPT and LLaMA). It shows perplexity scores (lower is better) and zero-shot accuracy (higher is better) on various benchmark datasets (Wiki2, C4, Winograd Schema Challenge, HellaSwag, Physical Interaction QA, BoolQ, ARC-e, ARC-c). The FP16 row serves as the upper bound performance representing the full-precision model. The table highlights the superior performance of OneBit, especially noticeable in larger models.
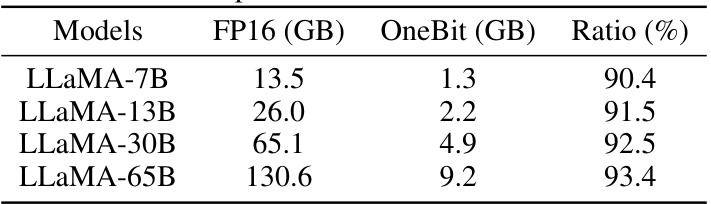
This table shows the compression ratios achieved by the OneBit method on various sizes of LLaMA models. It compares the memory footprint (in gigabytes) of the original FP16 models to the compressed OneBit models (using 1-bit weights). The ratio column shows the percentage reduction in memory usage due to the OneBit compression technique.
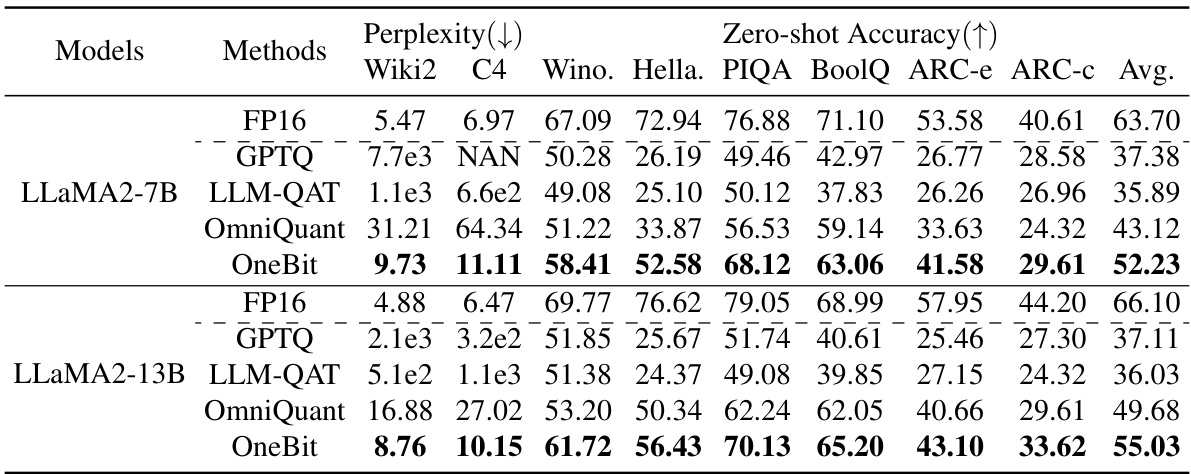
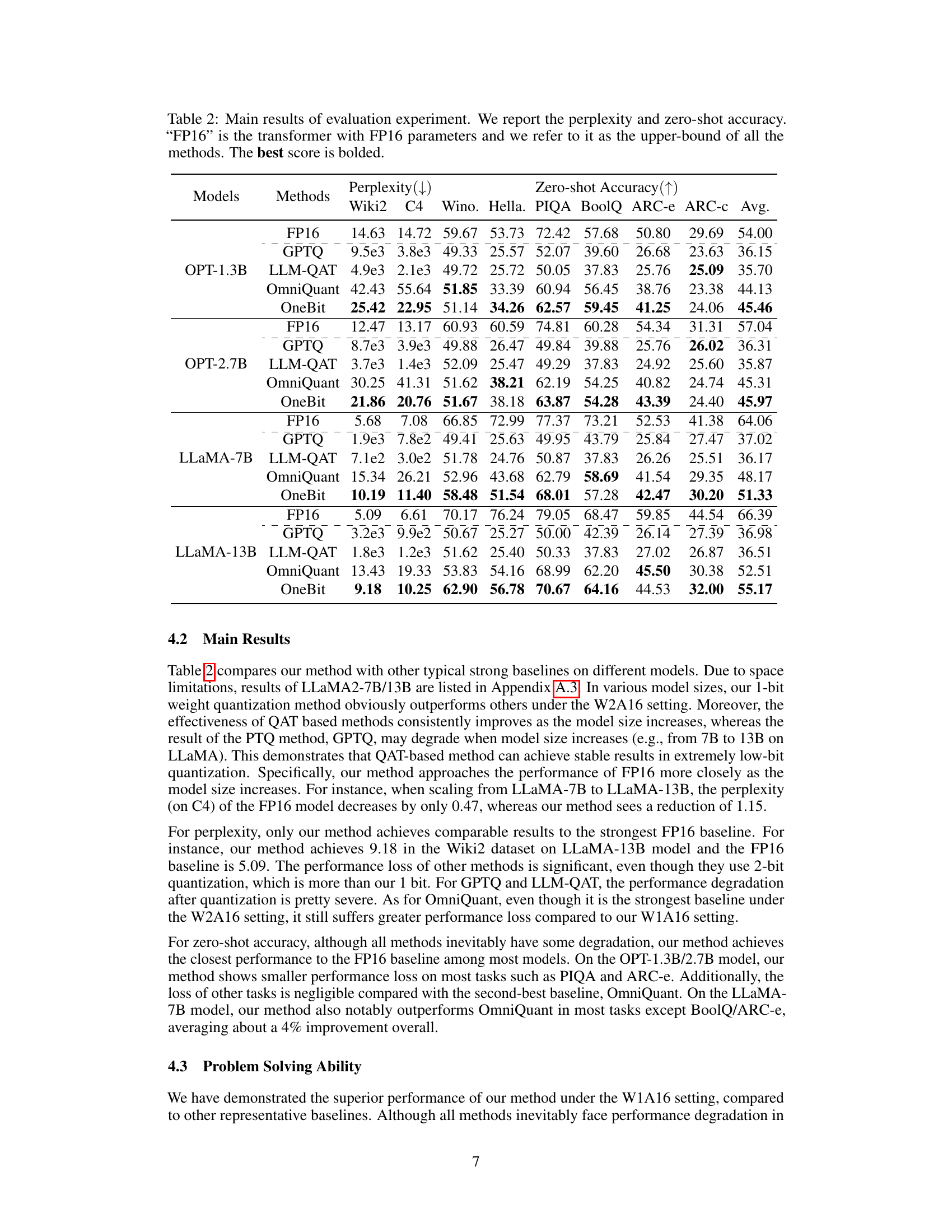
This table presents the main experimental results, comparing the performance of the proposed OneBit method against several baselines (GPTQ, LLM-QAT, OmniQuant) and the full-precision FP16 model. It shows perplexity scores (lower is better) and zero-shot accuracy (higher is better) across various tasks (Wiki2, C4, Winograd Schema Challenge, HellaSwag, PIQA, BoolQ, ARC-e, ARC-c) for different model sizes (OPT-1.3B, OPT-2.7B, LLaMA-7B, LLaMA-13B). The FP16 column represents the upper bound performance, showcasing the effectiveness of OneBit in achieving high performance with extremely low-bit quantization.

This table presents the main results of the evaluation experiments. It compares the performance of the proposed OneBit method against several baselines (GPTQ, LLM-QAT, OmniQuant) across different model sizes (OPT-1.3B/2.7B, LLaMA-7B/13B). The metrics reported include perplexity (lower is better) on the WikiText2 and C4 datasets, and zero-shot accuracy on various downstream tasks (Winograd, HellaSwag, PIQA, BoolQ, ARC-e, ARC-c). The FP16 results serve as an upper bound for comparison.
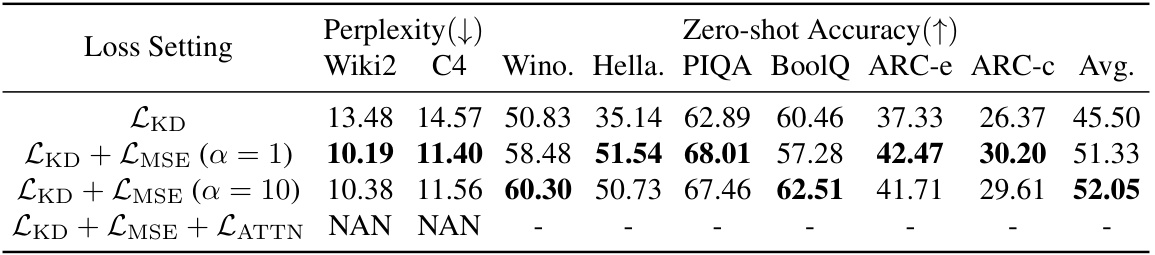
This table presents the results of an ablation study conducted on the LLaMA-7B model to evaluate the effectiveness of different loss functions used in the knowledge distillation process. The study compares the performance of using only the knowledge distillation loss (LKD) against versions that incorporate mean squared error loss (LMSE) with different weighting parameters (α) and attention score alignment loss (LATTN). The results are evaluated using perplexity and zero-shot accuracy across several benchmarks (Wiki2, C4, Winograd Schema Challenge, HellaSwag, Physical Interaction QA, BoolQ, ARC-e, and ARC-c). The table shows that combining LKD with LMSE leads to improved results, particularly when α = 1.
Full paper#