Approximation Rate of the Transformer Architecture for Sequence Modeling

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial for researchers in sequence modeling because it provides a theoretical foundation for understanding the Transformer’s approximation capabilities. It introduces novel complexity measures and derives explicit approximation rates, enabling a more precise comparison with other sequence models. This opens avenues for designing more efficient and targeted Transformer architectures.

Visual Insights

#

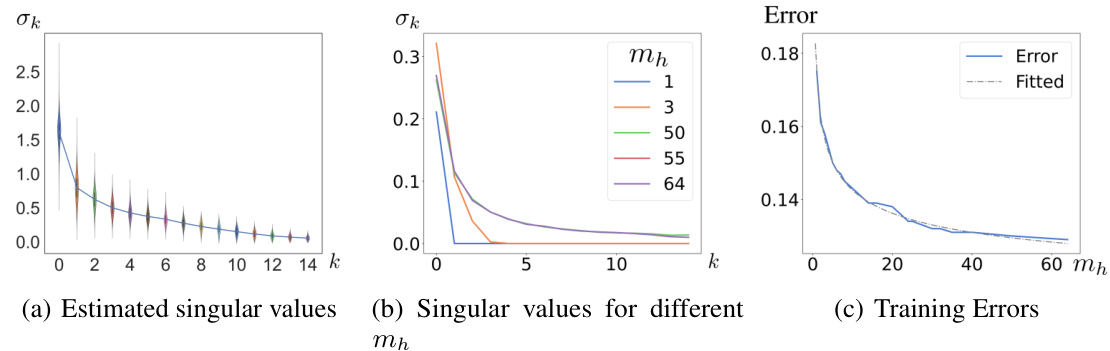
Figure 1 presents the results of estimating the rank of the attention matrix from sampled data in a Vision Transformer model applied to the CIFAR10 dataset. (a) shows the distribution of singular values for mh=64. (b) shows how the singular value distribution changes as the attention head size (mh) increases during training. (c) shows how the training error changes as mh increases. The findings show that as mh increases to a sufficiently large value, the decaying pattern of the singular values converges, suggesting the presence of a low-rank structure. The error decreases with mh following a power law decay, consistent with the approximation rate in Theorem 4.2.

This table presents the performance of the Transformer model on the CIFAR10 dataset (accuracy) and the WMT2014 English-German dataset (BLEU score). The ‘Original’ row shows the performance on the original datasets. The ‘Altered’ row shows the performance when the temporal ordering of the input sequences has been changed by applying a fixed permutation to the input, while keeping the output unchanged. The results demonstrate the Transformer’s relative insensitivity to changes in temporal ordering.

In-depth insights

#

Transformer Rate

#

The concept of “Transformer Rate” invites exploration of how efficiently transformer architectures approximate various sequence-to-sequence mappings. A key aspect would be defining appropriate complexity measures that capture the structural characteristics of the input sequences and target relationships. Jackson-type approximation rates, drawing parallels with polynomial approximation theory, could provide a theoretical framework for quantifying this efficiency. This analysis may reveal how well transformers handle different temporal structures, such as those exhibiting long-range dependencies or inherent orderings. Comparing these rates against traditional recurrent neural networks would highlight the strengths and limitations of each approach. The resulting insights would be valuable in understanding the strengths of transformers and also guide the design of future architectures that may better handle specific sequential relationships.

Approximation Space

#

The concept of an approximation space is crucial for understanding approximation theory, particularly in the context of function approximation. It represents a carefully selected subset of a larger function space, chosen to balance the complexity of functions within the space against their ability to approximate a target function. The choice of an approximation space directly influences the approximation rate, determining how quickly the error decreases as the complexity of approximating functions increases. In the paper, the approximation space is constructed based on complexity measures that capture both pairwise and pointwise relationships between input tokens. This novel approach allows for a more nuanced understanding of the Transformer’s approximation capabilities, distinguishing it from traditional recurrent models. A well-defined approximation space must be dense in the larger space, meaning it contains functions that can approximate any function in the larger space arbitrarily closely. This density ensures that the chosen space is not overly restrictive, while the complexity measures help to control the complexity of functions used for approximation, preventing overfitting and promoting generalization.

RNN Comparison

#

The RNN comparison section likely delves into a detailed analysis contrasting Recurrent Neural Networks (RNNs) with Transformers, focusing on their relative strengths and weaknesses in sequence modeling. Approximation rate is a crucial aspect, investigating how efficiently each architecture approximates various sequence-to-sequence mappings. The analysis likely explores different temporal structures, such as those with strong temporal ordering versus those exhibiting temporal mixing. A key finding might highlight how Transformers excel with low-rank structures, while RNNs perform better with specific types of temporal dependencies. The comparison likely goes beyond approximation rates, considering aspects like computational cost and efficiency, perhaps showing where one architecture outperforms the other depending on the data characteristics. The discussion may also involve architectural differences, comparing the mechanisms RNNs use (recurrent units) to those of Transformers (attention mechanisms), relating these differences to their performance on different tasks.

Temporal Effects

#

The concept of “Temporal Effects” in a research paper likely explores how the temporal structure of sequential data influences model performance. This could involve investigating how different architectures handle temporal ordering, for example, whether reversing the order of events significantly impacts predictions. The analysis might also delve into the impact of temporal dependencies, examining how far back in the sequence the model needs to look to make accurate predictions. Different types of temporal structures, such as those with regular intervals or irregular patterns, might be compared to assess their influence on model accuracy. Additionally, the research may consider how the model learns and represents temporal information, focusing on mechanisms like attention or recurrent connections that are crucial for capturing temporal dynamics. Furthermore, an important aspect could be evaluating how various complexities of temporal patterns impact a model’s capacity for generalization.

Future Research

#

Future research directions stemming from this work on Transformer approximation rates could involve extending the analysis to more complex architectures. Investigating multi-headed attention mechanisms and their impact on approximation capabilities is crucial. Similarly, analyzing deeper Transformer networks and how their layered structure affects approximation rates would provide valuable insights. Exploring different types of positional encodings and their influence on approximation would also be valuable. Furthermore, a more comprehensive comparison with other sequence modeling architectures beyond RNNs, such as recurrent convolutional networks or attention-augmented RNNs, would enrich the understanding of the Transformer’s strengths and weaknesses. Finally, empirical studies on diverse datasets and tasks are necessary to validate the theoretical findings and explore the practical implications of these approximation rate results, potentially focusing on scenarios with specific temporal structures where the Transformer excels or underperforms.

More visual insights

#

More on figures

This figure shows the results of estimating singular values and training errors for a vision transformer model on the CIFAR10 dataset. Subfigure (a) displays the distribution of estimated singular values for a model with 64 attention heads. Subfigure (b) compares the estimated singular values for models with varying numbers of attention heads (mh). Finally, subfigure (c) shows how the training error changes as the number of attention heads increases.

Figure 1 shows the results of estimating singular values from a trained vision transformer model on the CIFAR-10 dataset. Subfigure (a) displays the distribution of singular values for a model with 64 attention heads (mh=64). Subfigure (b) shows how the estimated singular values change as the number of attention heads (mh) varies. Finally, subfigure (c) shows the training error plotted against the number of attention heads (mh), indicating a relationship between model complexity and error.

This figure shows the results of estimating the singular values of the attention matrix in a Vision Transformer model trained on the CIFAR10 dataset. Subfigure (a) displays a violin plot showing the distribution of estimated singular values for a model with 64 attention heads (mh). Subfigure (b) compares the estimated singular values for models with different numbers of attention heads, demonstrating convergence as mh increases. Finally, subfigure (c) plots the training error against the number of attention heads, illustrating a power law decay consistent with the theoretical approximation rate.

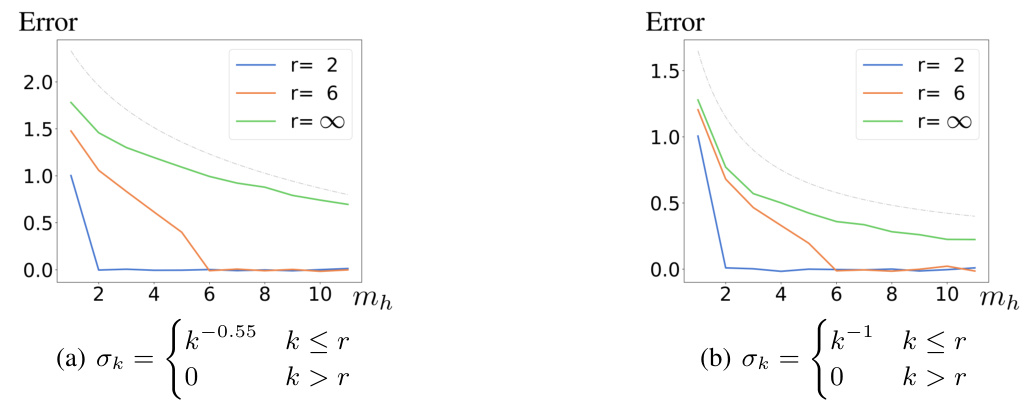
Figure 1 shows the results of experiments performed on a Vision Transformer model trained on the CIFAR-10 dataset. Subfigure (a) displays the distribution of estimated singular values of the attention matrix for a model with 64 attention heads (mh=64), visualized using violin plots. Subfigure (b) shows how the estimated singular values change as the number of attention heads (mh) varies. Finally, subfigure (c) shows the relationship between training error and the number of attention heads (mh).

More on tables

This table presents the Mean Squared Error (MSE) values achieved by Recurrent Neural Networks (RNNs) and Transformers on different temporal structures. The rows represent different alterations: Original (no alteration), Altered (Temporal Ordering changed), and Altered (Temporal Mixing applied). The columns indicate which model (RNN or Transformer) produced the results. The MSE values show the relative performance of the models in handling changes to the temporal structure of the sequential relationships.

This table presents the mean squared error (MSE) values obtained from RNN and Transformer models when tested on datasets without temporal ordering. The ‘Original’ row shows the MSE when the models are trained and tested on the original datasets. The ‘Permuted’ row shows the MSE when the input sequence is permuted but the output remains unchanged.

Full paper

#