Parameterized Approximation Schemes for Fair-Range Clustering

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial because it tackles the significant computational challenges in fair-range clustering, a critical area in data analysis where fairness across demographic groups is paramount. The first-ever parameterized approximation schemes for fair-range k-median and k-means problems in Euclidean spaces offer a significant advancement in algorithmic efficiency, paving the way for better real-world applications. It addresses the limitations of existing approaches and promotes fairer and more efficient data analysis techniques for researchers handling demographic data.

Visual Insights

#

Figure 1 illustrates two scenarios in the context of fair-range clustering. In (a), a client closest to an optimally opened facility (f*) is designated as a ’leader’. A search space (annulus) is created around this leader to find suitable facilities to open. In (b), a cell within the annulus is identified, and its center point (f) is selected as the facility to be opened in the approximate solution. This highlights the core difference in the proposed algorithm’s approach to facility selection compared to previous methods.

In-depth insights

#

Fair Clustering

#

Fair clustering addresses the critical issue of bias in traditional clustering algorithms. Standard methods often create clusters that disproportionately represent certain demographic groups, leading to unfair or discriminatory outcomes. Fair clustering aims to mitigate this by incorporating fairness constraints into the clustering process. This might involve ensuring proportional representation of each group across clusters or limiting the disparity in cluster sizes or characteristics between groups. The methods used can range from pre-processing data to modify the distribution to integrating fairness directly into the clustering objective function. Achieving fairness often involves a trade-off with clustering accuracy, requiring careful consideration of the appropriate balance. The choice of fairness metric is also vital, as different metrics prioritize different aspects of fairness. Research in fair clustering is ongoing, exploring various approaches and metrics to provide more equitable and unbiased clustering solutions. This is especially important in high-stakes applications, such as resource allocation, loan applications, and criminal justice.

Approx. Schemes

#

Approximation schemes are crucial for tackling computationally hard problems. In the context of fair-range clustering, the challenge lies in finding a balance between achieving fairness across demographic groups and minimizing the overall cost. Classical approximation algorithms often fall short in satisfying fairness constraints. Therefore, the development of parameterized approximation schemes becomes important. These schemes provide guaranteed approximation ratios within a time complexity that is tractable for practical instances, even when the number of facilities and demographic labels is relatively large. The key is to leverage the structural properties of the problem or metric space to design efficient algorithms. Euclidean spaces, for example, offer geometrical advantages that can be exploited to design algorithms with better approximation ratios compared to general metric spaces. Analyzing the trade-offs between approximation quality and running time is essential. A good approximation scheme balances these competing factors, providing a practical solution that is both accurate and efficient.

Euclidean Metrics

#

The concept of “Euclidean Metrics” in the context of fair-range clustering is crucial because it leverages the inherent properties of Euclidean space to improve the efficiency and approximation guarantees of algorithms. Traditional fair-range clustering algorithms often struggle with high dimensionality and complex constraints. By focusing on Euclidean metrics, the algorithm can exploit geometric properties like triangle inequality and the ability to efficiently construct nets to design approximation schemes with fixed-parameter tractable running times. Dimensionality reduction techniques, such as the Johnson-Lindenstrauss transform, become valuable tools for preprocessing high-dimensional Euclidean data before applying the core algorithm. The use of Euclidean space simplifies the search for optimal facility locations, allowing for a more efficient and effective approximation of the fair-range k-median and k-means problems. The paper likely demonstrates how the geometric structure of Euclidean space can lead to superior algorithmic performance compared to more general metric spaces, where similar guarantees might be significantly harder to obtain.

FPT Algorithms

#

This research paper explores the realm of fixed-parameter tractable (FPT) algorithms, focusing on their application to fair-range clustering problems. The core idea is to leverage the inherent structure of these problems to design algorithms whose runtime is not solely determined by the input size, but also by specific parameters that are often relatively small in practice. This approach is particularly relevant for fair-range k-median and k-means problems, which are known to be computationally challenging. The paper likely presents novel FPT approximation schemes, offering significant improvements over existing algorithms by achieving (1+ε)-approximation ratios. A crucial aspect is the parameterization strategy, likely employing the number of facilities and demographic labels as key parameters. This would allow for efficient solutions even in cases with large datasets, provided the parameters remain reasonably small. The algorithms’ design might involve advanced techniques from parameterized complexity and approximation algorithms, possibly incorporating intricate methods for data reduction, searching, or dynamic programming. The results showcase the power of FPT algorithms in tackling computationally hard fair-range clustering problems, offering a potentially impactful advancement in the field of fair machine learning. The work’s significance lies not just in improved runtime, but also in its potential to enable fairer and more equitable clustering solutions in real-world applications.

Future Work

#

The paper’s exploration of parameterized approximation schemes for fair-range clustering opens several avenues for future work. Extending the approach to handle more complex fairness constraints beyond simple lower and upper bounds on facility assignments per demographic group is crucial. This could involve incorporating more sophisticated fairness metrics or addressing intersectional fairness. Investigating the impact of different distance metrics beyond Euclidean space is another important direction, particularly for applications where data does not naturally conform to Euclidean geometry. The current work’s focus on k-median and k-means algorithms suggests opportunities to explore other clustering objectives, like k-center or k-medoids, within the fair-range setting. Finally, developing more efficient algorithms is essential, as the current algorithms’ running times might be prohibitive for large-scale datasets. This could involve the design of improved approximation algorithms or heuristic methods suitable for practical applications.

More visual insights

#

More on figures

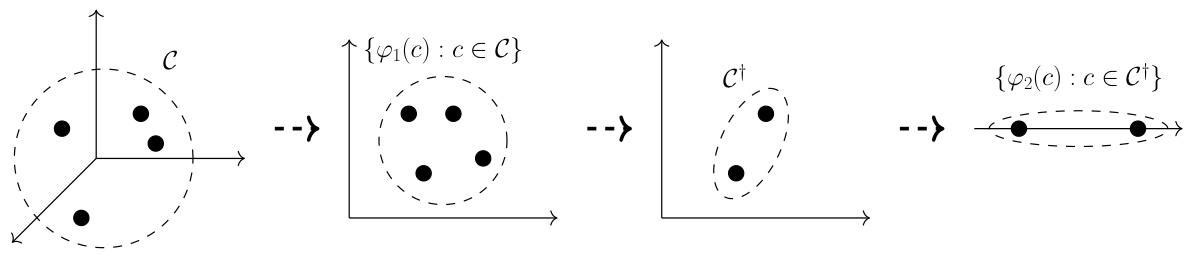
This figure illustrates the data reduction process used in Algorithm 1. It starts with a set of clients C in a high-dimensional space (R^d). First, a dimensionality reduction technique (φ₁) maps these clients to a lower-dimensional space (R^d*). Then, a coreset C^† (a smaller, weighted subset that approximates the larger dataset) is constructed from the reduced data. Finally, another mapping (φ₂) projects the coreset back to the original dimensionality (R^d). This process reduces the computational burden while retaining important properties of the dataset.

This figure illustrates two scenarios in the fair-range clustering algorithms. (a) shows the traditional approach where an annulus is created around the client closest to the optimal facility f*. The algorithm then selects facilities within this annulus. (b) presents the improved approach proposed in the paper. Here, the annulus is divided into smaller cells, and the center of the cell containing the optimal facility is chosen as the opened facility. This approach aims to reduce the distance between selected and optimal facilities, improving approximation accuracy.

Full paper

#