↗ OpenReview ↗ NeurIPS Proc. ↗ Chat
TL;DR#
The research explores ‘benign overfitting’, a phenomenon where models perfectly fit noisy training data yet generalize well. Existing studies largely focused on linear models or assumed unrealistic near-orthogonality of input features, limiting practical relevance. This paper investigates benign overfitting in two-layer leaky ReLU networks with the hinge loss, a more realistic and widely-used setting.
The researchers used a novel approach focusing on the signal-to-noise ratio of the model parameters and an ‘approximate margin maximization’ property. They demonstrated both benign and non-benign overfitting under less restrictive conditions, requiring only a linear relationship between input dimension and sample size (d = Ω(n)). Their theoretical findings provide tighter bounds for generalization error in different scenarios, offering a more complete and applicable understanding of this important phenomenon.
Key Takeaways#
Why does it matter?#
This paper is crucial because it challenges existing assumptions about benign overfitting in neural networks. By demonstrating benign overfitting with only a linear relationship between input dimension and sample size (d = Ω(n)), it opens up new research avenues for understanding this phenomenon in more realistic settings. This work also provides tight bounds for both benign and harmful overfitting, offering a more comprehensive theoretical understanding of the phenomenon.
Visual Insights#
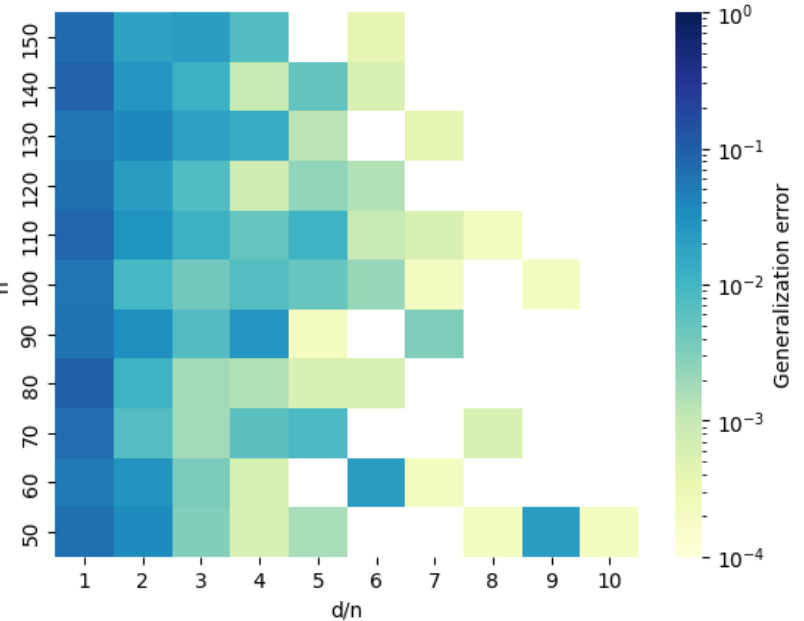
This figure shows the generalization error of a two-layer leaky ReLU network as a function of the ratio of input dimension to sample size (d/n) and sample size (n). The network was trained using gradient descent on the hinge loss until the training loss reached zero. The color of each cell represents the generalization error, with darker colors indicating lower error. The figure demonstrates that for a fixed d/n ratio, the generalization error decreases as n increases, and for a fixed n, the generalization error decreases as d/n increases. This behavior is consistent with the theoretical findings of benign overfitting described in the paper, showing that with sufficiently large n and d/n, even with noisy training data, a low generalization error can be achieved.
Full paper#



















