↗ OpenReview ↗ NeurIPS Proc. ↗ Chat
TL;DR#
Mechanism design often relies on perfect information about agents’ preferences. However, real-world scenarios frequently have incomplete or inaccurate information. This paper revisits mechanism design using a learning-augmented framework, where the mechanism receives imperfect predictions. Existing methods primarily use predictions about agent types, while this approach innovatively leverages predictions about the output. This introduces new challenges and requires novel analysis techniques.
The paper proposes a new universal measure, “quality of recommendation”, to evaluate mechanisms in various settings. The authors then demonstrate the application of this framework in several well-studied mechanism design paradigms. They develop new mechanisms and improve the analysis of existing ones, using the quality of recommendation as the evaluation metric. Further, they explore the limitations of existing strategyproof mechanisms in this setting. The overall contribution is a more practical and robust approach to mechanism design in scenarios with imperfect information.
Key Takeaways#
Why does it matter?#
This paper is important because it introduces a novel framework for mechanism design that leverages imperfect predictions. This is crucial because it bridges the gap between the optimistic predictions of machine learning models and the pessimistic guarantees of traditional mechanism design. The proposed approach allows for designing algorithms that perform well when predictions are accurate, but also provide worst-case guarantees even when predictions are inaccurate, thus offering a robust and practical approach to solve various problems. The new metric for evaluating mechanisms, “quality of recommendation”, provides a significant contribution.
Visual Insights#
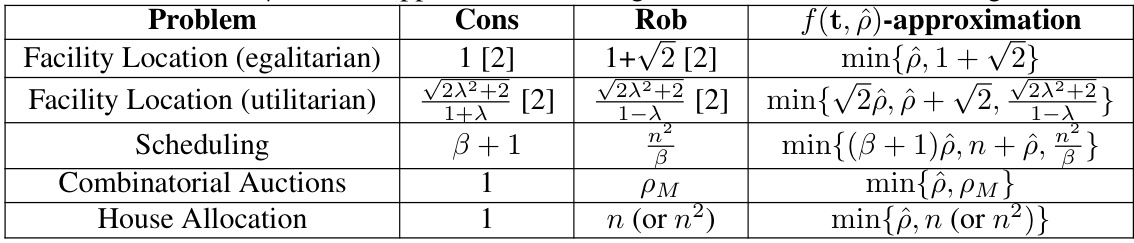
This table summarizes the main results of the paper. For each of the studied mechanism design problems (Facility Location, Scheduling, Combinatorial Auctions, and House Allocation), it shows the consistency (Cons), robustness (Rob), and approximation guarantees achieved by the proposed mechanisms. The approximation guarantees are expressed as functions of the quality of recommendation (ô), a novel metric introduced in the paper, as well as other relevant parameters (λ for Facility Location, β for Scheduling). The table highlights the trade-offs between consistency and robustness for each problem and the improvements obtained by using output recommendations.
Full paper#



















