Learning Linear Causal Representations from General Environments: Identifiability and Intrinsic Ambiguity

↗ OpenReview ↗ NeurIPS Proc. ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial because it tackles the challenge of causal representation learning in realistic settings where only observational data from diverse environments is available, rather than relying on unrealistic single-node interventions. This advances the field by providing theoretical guarantees on identifiability and proposing a novel algorithm, paving the way for more robust and reliable causal AI systems.

Visual Insights

#

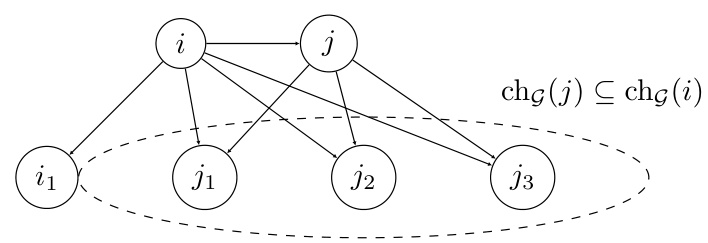
This figure illustrates Definition 3 from the paper, which defines the concept of a ‘surrounding set’ in a causal graph. Node ‘j’ is surrounded by node ‘i’ (i ∈ surg(j)) if ‘i’ is a parent of ‘j’, and all children of ‘j’ are also children of ‘i’. The dashed ellipse highlights the children of node ‘j’, demonstrating that they are a subset of the children of node ‘i’. This concept is crucial to understanding the intrinsic ambiguities in causal representation learning discussed in the paper.

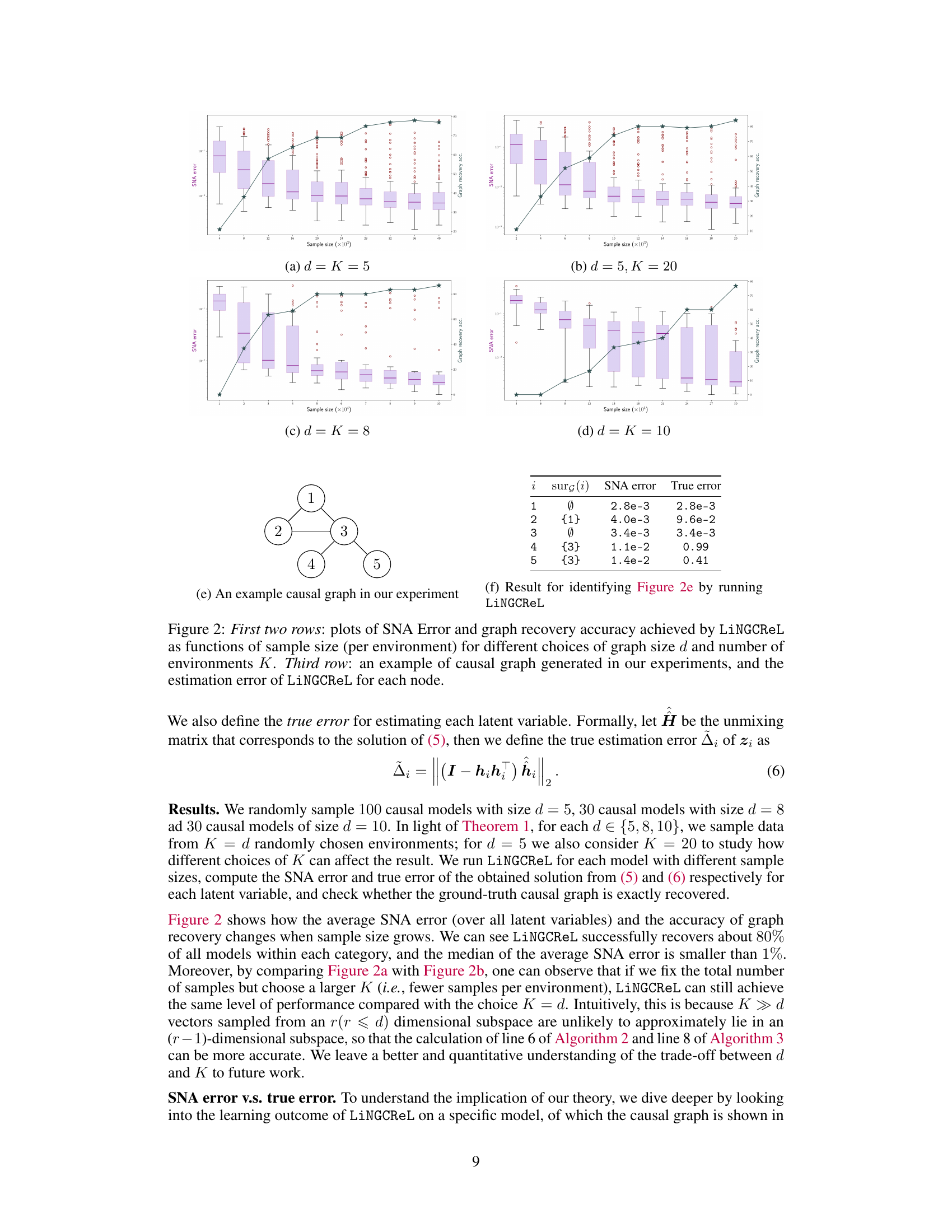
This figure shows the performance of the LiNGCREL algorithm in recovering the causal graph and estimating latent variables under different experimental settings. The top two rows present box plots illustrating the SNA (Surrounded-Node Ambiguity) error and graph recovery accuracy at various sample sizes, for different graph sizes (d) and numbers of environments (K). The bottom row provides a specific example causal graph, along with the SNA error and true error for each node, illustrating the algorithm’s performance at different scales.

In-depth insights

#

Linear CRL ID

#

The heading ‘Linear CRL ID’ likely refers to the identifiability problem within the framework of linear causal representation learning (CRL). Linearity simplifies the model, making analysis tractable but potentially limiting the real-world applicability. Identifiability addresses the core challenge: can the underlying causal graph and latent variable relationships be uniquely recovered from observed data? The ‘ID’ part highlights the central focus on establishing conditions that guarantee identifiability, possibly under specific assumptions on data generation or interventions. A key insight to explore would be whether the paper proves identifiability under these linear constraints, offering theoretical guarantees, and perhaps also introduces algorithms designed to achieve this identification in practice. The in-depth analysis should also investigate the limitations of linear CRL concerning real-world complexities and consider how the results might extend to more general non-linear models. It’s crucial to check if the paper addresses the unavoidable ambiguities inherent in causal discovery and how these are handled within the linear CRL setting.

Surrounded Ambiguity

#

The concept of “Surrounded Ambiguity” in causal representation learning highlights a fundamental limitation in identifying causal relationships from observational data, even under seemingly ideal conditions. It suggests that certain latent variables’ effects can be indistinguishable from those of their “surrounding” nodes due to overlapping influence on downstream variables. This ambiguity is intrinsic, meaning it’s not merely a consequence of insufficient data or weak modeling assumptions; rather, it’s a structural property of the causal system itself. The presence of surrounded ambiguity underscores the challenge of uniquely identifying a causal graph given observational data. Even linear causal models and linear mixing functions are susceptible to this problem, illustrating its pervasiveness. Overcoming surrounded ambiguity necessitates moving beyond purely observational data, potentially requiring interventions or incorporating strong prior knowledge about the causal structure to constrain the model space and achieve identifiability.

LiNGCREL Algorithm

#

The LiNGCREL algorithm, proposed for linear non-Gaussian causal representation learning, tackles the challenge of identifying causal relationships from data generated in diverse, real-world environments. Unlike previous methods that rely on unrealistic single-node interventions, LiNGCREL leverages data from multiple environments without strong assumptions about their similarities. The algorithm’s core innovation is an effect cancellation scheme that uses orthogonal projections to efficiently determine the dependencies between latent variables, allowing it to recover the ground truth causal model up to a surrounded-node ambiguity (SNA). LiNGCREL provably recovers the model in the infinite-sample regime and demonstrates effectiveness in finite-sample experiments. Its ability to handle general environments is significant, as it moves beyond the limitations of previous methods and opens possibilities for more realistic causal inference in complex systems. The algorithm’s reliance on linear models and the assumption of non-Gaussian noise are crucial limitations; further investigation into non-linear settings and robustness to Gaussian noise would enhance its practical applicability and extend its contributions to the field of causal representation learning.

Diverse Environments

#

The concept of “Diverse Environments” in causal representation learning is crucial for identifiability. It posits that utilizing data from varied settings, each offering a unique perspective on the causal relationships between variables, significantly improves the ability to disentangle true cause-and-effect from spurious correlations. The diversity stems not merely from different data distributions but also from variations in environmental conditions that influence how those relationships manifest. This approach tackles the limitations of traditional methods that rely on single-environment data, which often suffer from non-identifiability due to confounding factors or hidden variables. By leveraging the contrasts and overlaps observed across multiple environments, algorithms can better isolate true causal effects, leading to more robust and accurate causal models. The challenge lies in effectively utilizing this diversity—developing methods that can robustly handle diverse data formats and extract meaningful information while accounting for various sources of noise and bias inherent in real-world data from different environments. The ultimate goal is to create AI systems that are not only statistically accurate but also causally informed, enabling them to generalize better to unseen situations and make more reliable predictions in complex, dynamic environments.

General CRL Limits

#

The heading ‘General CRL Limits’ suggests an investigation into the fundamental boundaries of causal representation learning (CRL). A thoughtful analysis would likely explore limitations arising from data scarcity, model complexity, and the inherent ambiguity in inferring causal relationships from observational data. Identifiability issues, a central challenge in CRL, would be a major focus, examining scenarios where multiple causal models could explain the observed data equally well. The analysis might delve into the trade-offs between making strong assumptions (e.g., linearity, specific noise distributions) to achieve identifiability and the resulting loss of generality. Computational constraints and the scalability of CRL algorithms to large datasets or high-dimensional problems could also be discussed, highlighting the practical limitations of existing methods. Ultimately, a comprehensive exploration of ‘General CRL Limits’ would provide valuable insights into the current state-of-the-art and guide future research directions, helping to identify promising avenues for overcoming these limitations and making CRL more robust and widely applicable.

More visual insights

#

More on figures

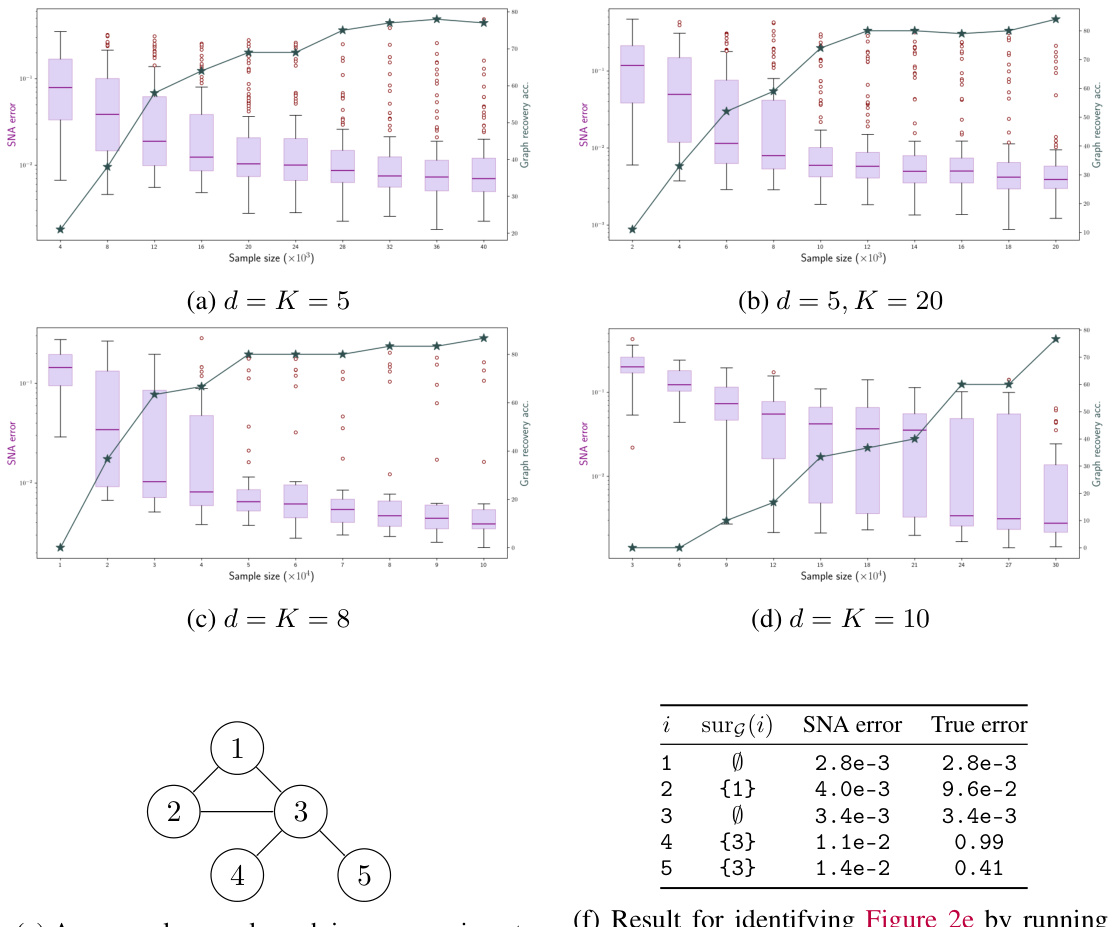
This figure shows the performance of the LiNGCREL algorithm on synthetic data with varying sample sizes and numbers of environments. The top two rows present box plots illustrating the SNA error and graph recovery accuracy. The bottom row displays an example causal graph used in the experiments along with the error metrics produced by the algorithm for each node in that graph. The results demonstrate the algorithm’s ability to accurately recover causal relationships, especially at larger sample sizes.

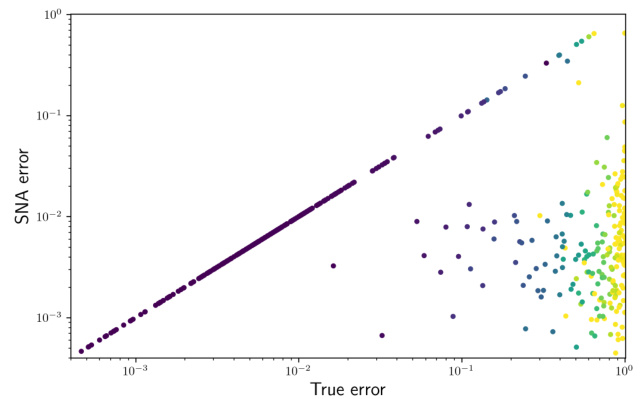
This figure shows the results of the LiNGCREL algorithm. The first two rows present box plots illustrating the SNA error and graph recovery accuracy, varying the sample size, graph size (d), and number of environments (K). The third row displays a sample causal graph from the experiments and the corresponding estimation errors produced by LiNGCREL for each node in the graph. The plots visualize how the algorithm’s performance changes as the sample size increases and for different model complexities.

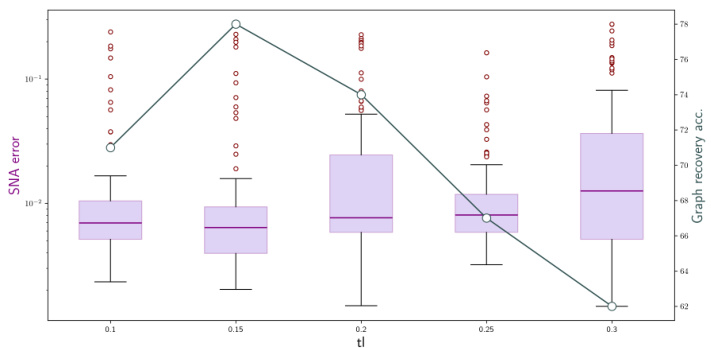
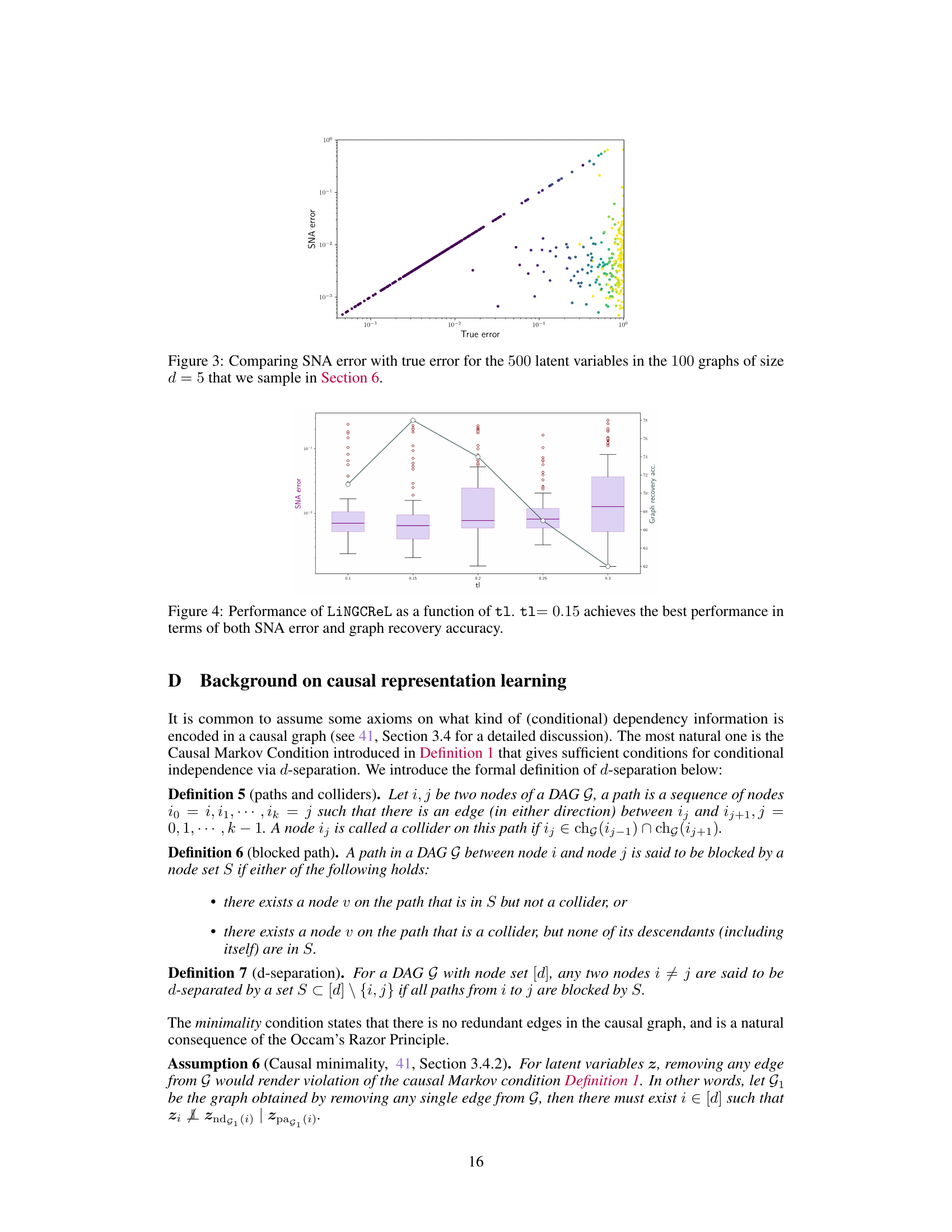
This figure displays the performance of the LiNGCREL algorithm as a function of its hyperparameter t1. The y-axis shows both the SNA error (on a logarithmic scale) and the graph recovery accuracy (on a linear scale). The x-axis represents the different values of t1 tested. The box plots show the distribution of the performance metric for multiple trials. The figure demonstrates that the algorithm achieves its best performance when t1 is set to 0.15, indicating an optimal balance between robustness to noise and accurate identification of the causal structure.

Full paper

#