↗ OpenReview ↗ NeurIPS Proc. ↗ Chat
TL;DR#
Current metagenomic binning often relies on computationally expensive genome foundation models. These models, while accurate, struggle with the massive datasets generated by modern sequencing technologies. This poses a significant challenge for researchers, who need efficient methods to analyze large microbial communities.
This research introduces a new, lightweight metagenomic binning approach based on k-mer composition. By revisiting the theoretical foundations of k-mers, they developed a scalable model with comparable accuracy to large foundation models but using far fewer computational resources. The model’s efficiency enables the analysis of massive, real-world datasets, offering a practical solution for metagenomic studies and paving the way for more comprehensive microbiome research.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in metagenomics and bioinformatics due to its scalable and efficient k-mer based model for metagenomic binning. It offers a lightweight alternative to computationally expensive genome foundation models, providing comparable performance with significantly reduced resource requirements. This opens new avenues for analyzing large-scale real-world datasets and accelerates progress in microbiome research.
Visual Insights#
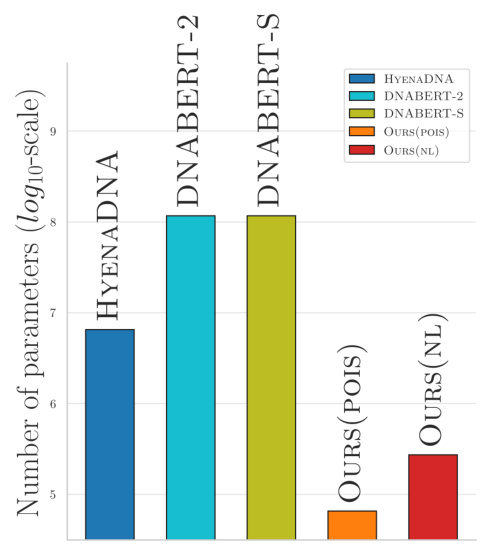
This figure compares the number of parameters (on a logarithmic scale) of several models used for genome representation learning, including three state-of-the-art genome foundation models (HYENADNA, DNABERT-2, DNABERT-S) and two k-mer based models proposed in the paper (OURS (POIS) and OURS (NL)). It highlights the significantly smaller number of parameters required by the k-mer based models compared to the genome foundation models, emphasizing their improved scalability.

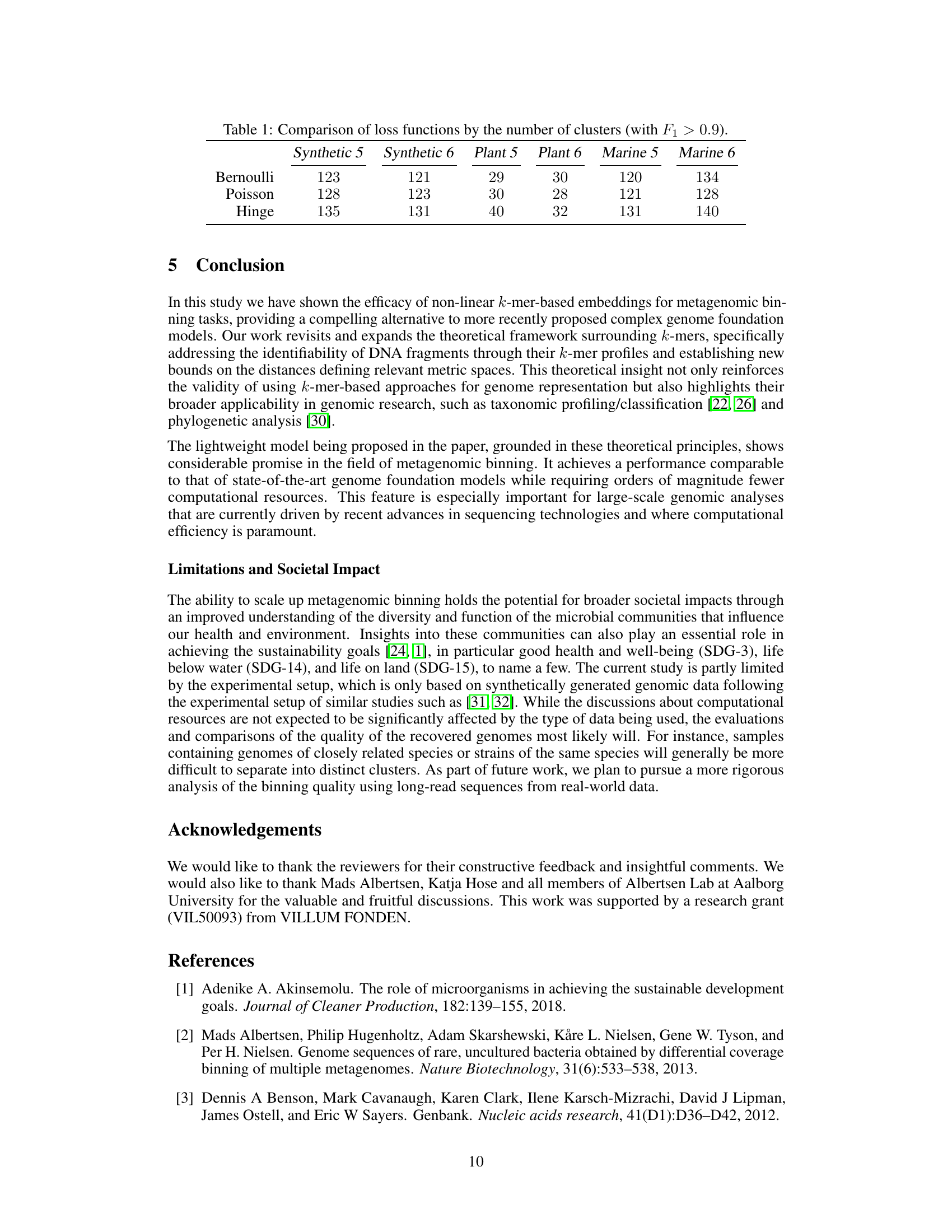
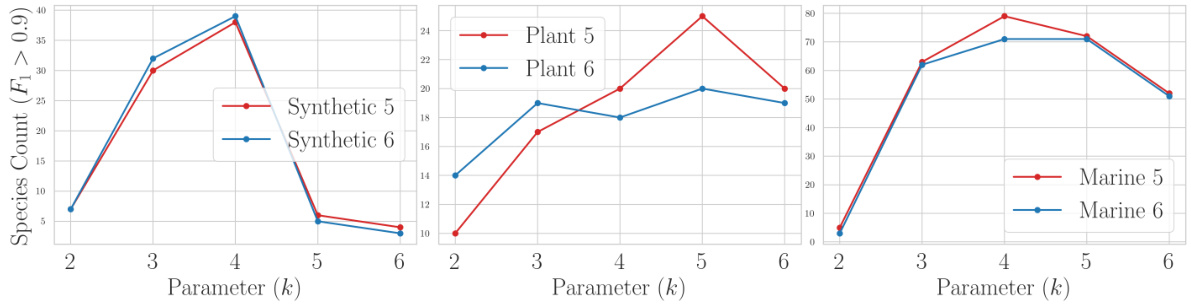
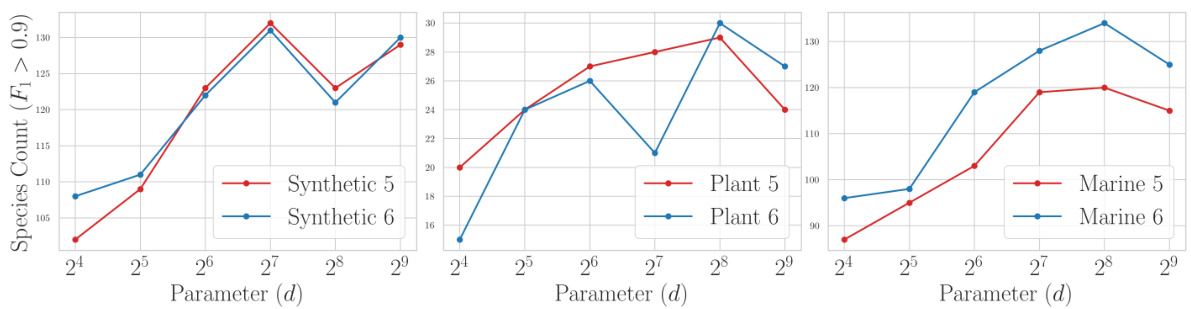
This table presents a comparison of three different loss functions (Bernoulli, Poisson, and Hinge) used in the proposed non-linear k-mer embedding model for metagenomic binning. The comparison is based on the number of clusters achieving an F1 score greater than 0.9 across six different datasets: Synthetic 5, Synthetic 6, Plant 5, Plant 6, Marine 5, and Marine 6. Each dataset represents a different metagenomic community.
In-depth insights#
K-mer Theory Revisited#
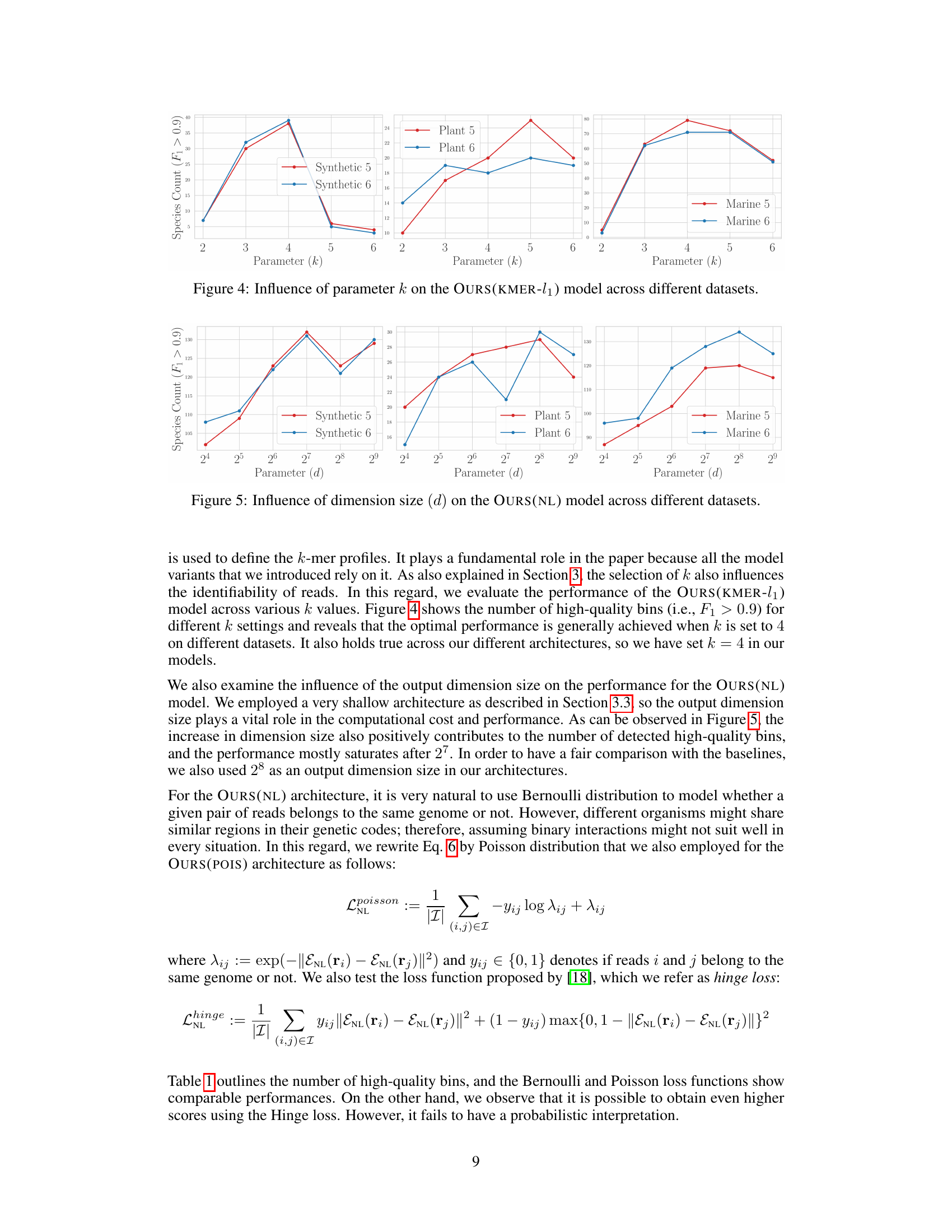
A revisit of k-mer theory in genomics reveals significant potential for enhancing genome representation learning. The core idea revolves around leveraging the frequency of k-mers (short DNA subsequences) to represent longer sequences, offering a computationally efficient and scalable alternative to more complex deep learning models. This approach is particularly attractive for metagenomic binning where massive datasets are common. The theoretical analysis delves into the identifiability of DNA fragments based solely on their k-mer profiles, establishing bounds on the distance between fragments with similar k-mer compositions. This foundational work justifies the use of k-mers and allows the development of novel models that are not only accurate but also highly scalable, crucial for handling the immense real-world datasets frequently encountered in genomic studies. The paper demonstrates the efficacy of the revisited k-mer approach by showcasing its comparable performance to state-of-the-art deep learning models but with significantly reduced computational costs. This scalability advantage is a key strength, offering a practical and effective solution for metagenomic binning and related tasks.
Embedding Models#
The paper explores embedding models for genome representation, focusing on k-mer based approaches as a lightweight and scalable alternative to computationally expensive genome foundation models. The authors provide a theoretical analysis of k-mer identifiability, establishing bounds on edit distances based on l1 distances between k-mer profiles. This analysis justifies the use of k-mers and supports the design of linear and non-linear embedding models. The linear models, including a simple k-mer profile model and a Poisson model leveraging k-mer co-occurrence, serve as baselines. A novel non-linear model employing self-supervised contrastive learning is proposed to capture complex relationships within the genomic data. The study highlights the comparative performance of these k-mer based models against large state-of-the-art genome foundation models, demonstrating their effectiveness in metagenomic binning tasks while exhibiting significantly improved scalability. Scalability is a critical aspect given the massive datasets generated by modern sequencing technologies. The theoretical analysis and empirical validation contribute significantly to the advancement of efficient and effective genome representation learning.
Metagenomic Binning#
Metagenomic binning is a crucial computational step in metagenomics, aiming to decompose complex mixtures of DNA sequences from environmental samples into individual genomes representing different microbial organisms. The challenge lies in the high dimensionality and noise inherent in sequencing data, requiring sophisticated computational methods. Current approaches often leverage genome representations, such as k-mer profiles or embeddings learned through deep learning models, to cluster similar sequences. K-mer profiles, while computationally efficient, lack contextual information, limiting their accuracy. Advanced techniques like genome foundation models have emerged, improving performance but at the cost of significantly increased computational demands. The paper explores a balanced approach that builds upon the strengths of k-mer representations, proposing theoretical justifications for their effectiveness and demonstrating that efficient and lightweight k-mer based models can achieve comparable performance to large-scale foundation models, hence addressing the crucial need for scalable metagenomic binning techniques.
Scalability & Efficiency#
The research paper emphasizes the critical need for scalable and efficient methods in genome analysis, particularly in metagenomic binning. Traditional approaches, while effective, often struggle with the massive datasets generated by modern sequencing technologies. The authors highlight the computational limitations of existing genome foundation models, which, despite their impressive performance, are too resource-intensive for large-scale real-world applications. In contrast, k-mer-based embeddings are presented as a lightweight and scalable alternative, offering comparable accuracy while significantly reducing computational burden. This superior scalability is a crucial advantage, enabling the analysis of massive datasets associated with real-world metagenomic binning tasks. The theoretical analysis of k-mer profiles provides a firm foundation for the proposed approach, supporting its effectiveness and efficiency. Ultimately, the study underscores the importance of balancing accuracy and scalability in genome analysis and demonstrates the potential of k-mer methods in meeting the demands of high-throughput sequencing data.
Future Directions#
Future research could explore advanced k-mer embedding techniques, moving beyond linear and simple non-linear models to incorporate more sophisticated architectures like transformers or graph neural networks, potentially capturing higher-order dependencies within genomic sequences. Investigating alternative distance metrics and clustering algorithms beyond those used in this study could also improve accuracy and scalability. Theoretical analysis could be extended to formally address the identifiability of DNA fragments under more realistic noise conditions prevalent in real-world sequencing data. The efficacy of the proposed approach on various types of genomic datasets and their robustness to different levels of noise and sequencing errors warrants further investigation. Applying the k-mer embedding framework to other genome analysis tasks, such as phylogenetic tree reconstruction and gene prediction, is another promising direction for future work. Finally, exploring the potential of the proposed scalable approach for handling the massive datasets generated by modern long-read sequencing technologies is crucial for real-world applications and improving our understanding of microbial communities.
More visual insights#
More on figures
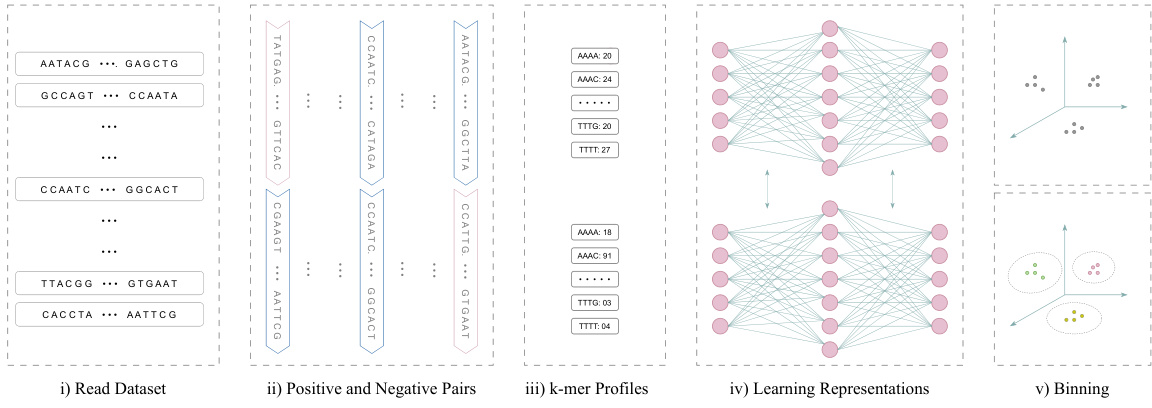
This figure illustrates the process of the non-linear k-mer embedding approach. It begins with a read dataset (i), showing multiple DNA sequences. These reads are then split into positive and negative pairs (ii). Positive pairs consist of two segments from the same read, while negative pairs combine segments from different reads. The k-mer profiles (iii) are calculated for each segment, which are then used as input for a neural network (iv). The neural network learns representations for the k-mer profiles. Finally, the learned representations are used for metagenomic binning (v), clustering the reads based on their genomic origins.
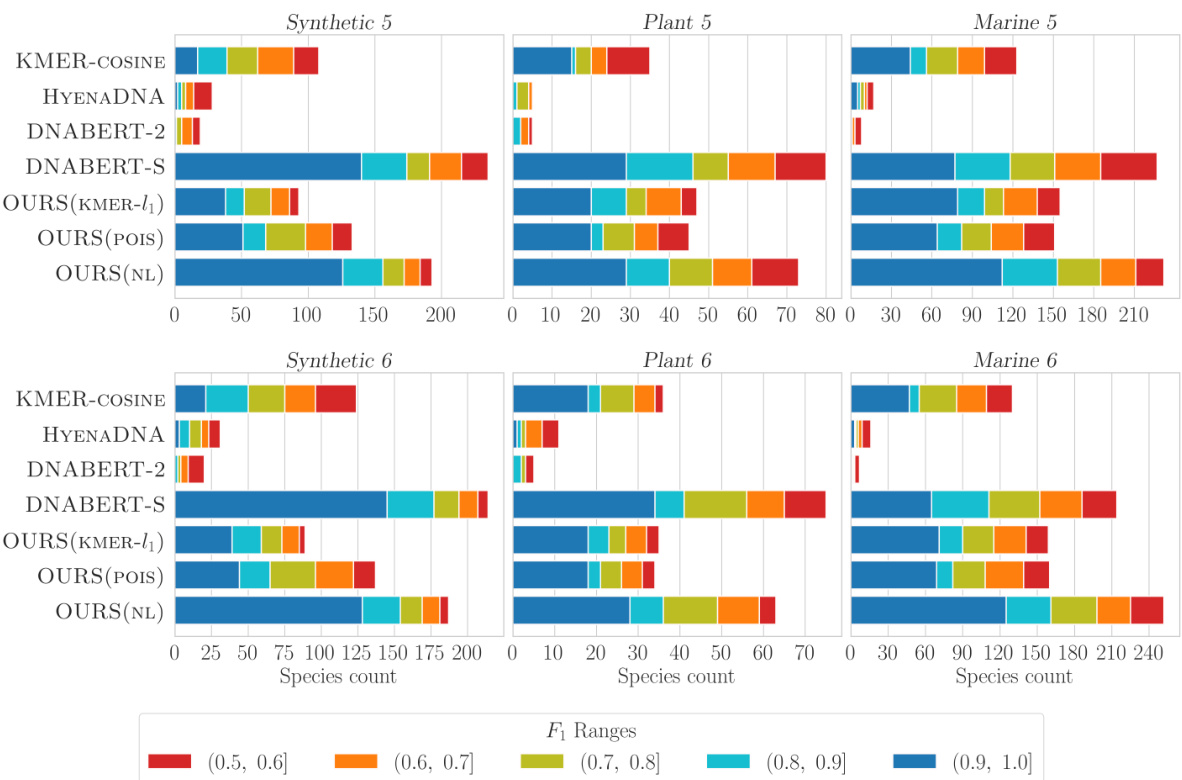
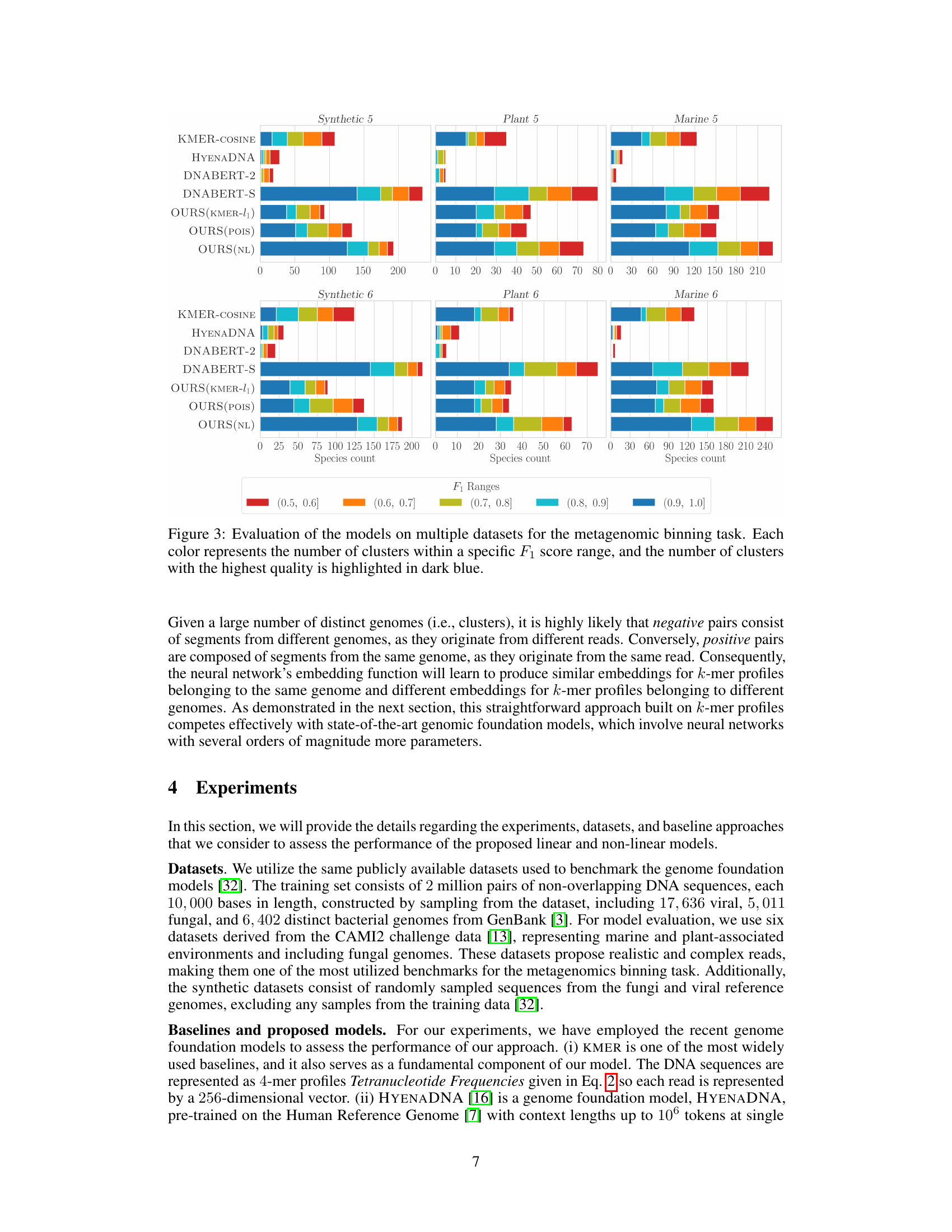
This figure shows the performance of different models (KMER-COSINE, HYENADNA, DNABERT-2, DNABERT-S, OURS(KMER-l1), OURS(POIS), OURS(NL)) on six different datasets (Synthetic 5, Plant 5, Marine 5, Synthetic 6, Plant 6, Marine 6) for the metagenomic binning task. Each bar represents the number of clusters achieved within a specific F1 score range (0.5-0.6, 0.6-0.7, 0.7-0.8, 0.8-0.9, 0.9-1.0). The color of the bar indicates the F1 score range, with darker blue representing higher-quality clusters (F1 score closer to 1.0). The figure allows for a visual comparison of the different models’ performance across various datasets and F1 score ranges, highlighting the effectiveness of the proposed models.
This figure evaluates the performance of different models on six metagenomic binning datasets (Synthetic 5, Synthetic 6, Plant 5, Plant 6, Marine 5, Marine 6). Each bar chart shows the distribution of the number of clusters obtained by each model, categorized by their F1 score ranges (0.5-0.6, 0.6-0.7, 0.7-0.8, 0.8-0.9, 0.9-1.0). The dark blue section within each bar represents the number of clusters with the highest quality (F1 score > 0.9). The models compared include KMER-COSINE, HYENADNA, DNABERT-2, DNABERT-S, and three variants of the proposed k-mer-based models (OURS). The figure allows for a visual comparison of the models’ performance across various datasets and F1 score thresholds, highlighting the relative strengths and weaknesses of each approach in recovering high-quality clusters.
This figure shows the performance of different models (KMER-COSINE, HYENADNA, DNABERT-2, DNABERT-S, OURS (KMER-l₁), OURS (POIS), OURS (NL)) on metagenomic binning tasks using multiple datasets (Synthetic 5, Synthetic 6, Plant 5, Plant 6, Marine 5, Marine 6). Each bar represents the number of clusters achieved within a certain F₁-score range (a measure of clustering accuracy). The darker blue color indicates the higher-quality clusters (higher F₁ score). The figure demonstrates the performance of the proposed models compared to existing state-of-the-art models, highlighting their effectiveness in terms of clustering accuracy.
More on tables
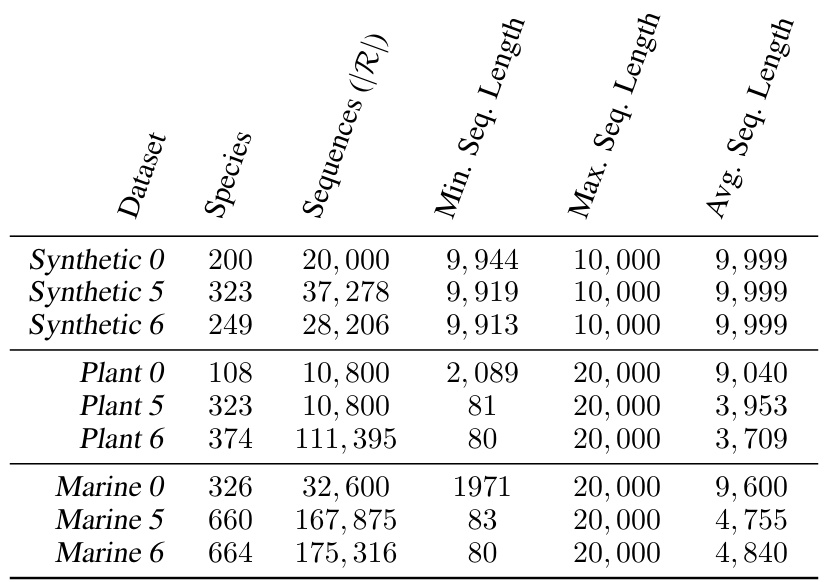
This table presents a statistical overview of the datasets employed in the paper’s experiments. It details the number of species, sequences, minimum sequence length, maximum sequence length, and average sequence length for various datasets categorized as Synthetic, Plant, and Marine, each with variants 0, 5, and 6. Dataset 0 is used for threshold determination in the K-medoid algorithm, while datasets 5 and 6 are used for model evaluation.

This table lists the symbols used in the paper and their corresponding descriptions. It provides a quick reference for understanding the notation used throughout the text, including mathematical formulas and algorithm descriptions.
Full paper#