↗ OpenReview ↗ NeurIPS Proc. ↗ Chat
TL;DR#
Deep learning’s success is attributed to efficient feature extraction. However, the mechanisms driving feature learning remain largely unclear, especially considering the contrasting ’lazy’ and ‘rich’ learning regimes. The ’lazy’ regime involves minimal parameter changes, while the ‘rich’ regime showcases substantial parameter adjustments, leading to improved generalization. This research investigates this issue by analyzing models that can transition between lazy and rich learning.
The study uses a minimal model with exact solutions to uncover how the initialization variance across layers determines the learning regime. This analysis is then extended to more complex linear models and shallow nonlinear networks, revealing how balanced and unbalanced initializations impact learning. Experiments demonstrate that unbalanced initializations, especially those promoting faster learning in earlier layers, can significantly accelerate feature learning and boost model interpretability. The results suggest a promising direction for research to leverage unbalanced initializations for improved training efficiency and model performance.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in deep learning as it provides a novel theoretical understanding of how initialization techniques influence the learning process and generalizes the findings to various network architectures. It motivates further exploration of unbalanced initializations to potentially enhance efficient feature learning. The findings could lead to better training strategies and improved model interpretability, which are highly relevant current research trends.
Visual Insights#
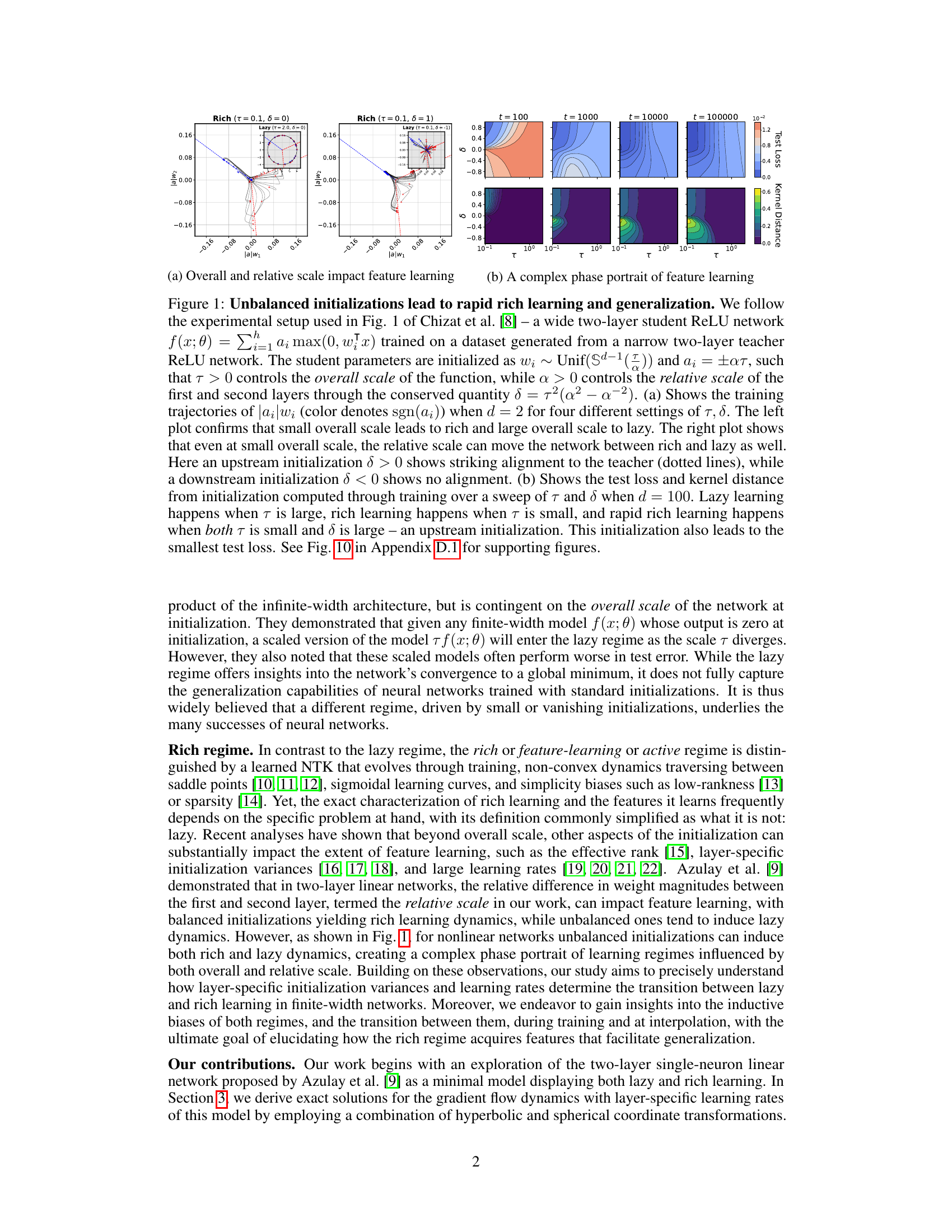
This figure demonstrates the impact of initialization on the learning regime of a two-layer ReLU network. Panel (a) shows training trajectories for different overall and relative scales, highlighting how unbalanced initializations (δ ≠ 0) can lead to rich learning (rapid feature learning) and good generalization. Panel (b) shows the effect of these parameters on test loss and kernel distance, further illustrating the superiority of unbalanced upstream initializations (δ > 0) for achieving rapid rich learning.
In-depth insights#
Unbalanced Init#
The concept of “Unbalanced Init,” likely referring to unbalanced initializations in neural network training, is a significant focus. The research suggests that carefully engineered imbalances in the initialization of layer-specific variances and learning rates can significantly boost the speed and efficiency of feature learning. This contrasts with the traditionally studied “balanced” or “lazy” training regimes. The core idea is that unbalanced initializations, particularly those favoring faster learning in earlier layers (upstream initialization), can lead to a more efficient exploration of the parameter space, accelerating the discovery of task-relevant features. The paper likely explores how conserved quantities, arising from these unbalanced initializations, constrain the geometry of the learning trajectories, shaping the learning dynamics. The implications are potentially substantial for improving training efficiency and model interpretability by enabling more focused feature extraction in deep learning architectures.
Rich vs Lazy#
The dichotomy of “rich” vs. “lazy” learning regimes in neural networks is a central theme in the paper. Rich learning is characterized by significant changes in the network’s internal representations (features) during training, resulting in non-linear learning dynamics and improved generalization. It is often associated with smaller, well-balanced initializations that allow the network to explore the parameter space more effectively. Lazy learning, conversely, involves minimal changes in the representations throughout training, essentially acting like a linear model and thus lacking flexibility and generalization capabilities. This regime tends to arise with large, unbalanced initializations which constrain learning to a small region of the loss landscape. The paper argues that carefully controlling the balance between initialization variances and learning rates across layers can strategically move the network between these two learning paradigms. This balance is determined by the relative scales of initializations across layers and has direct consequences on the geometry of the learning trajectory and feature learning. Understanding this dynamic interplay is crucial for designing more efficient and interpretable neural networks.
Linear Nets#
Research on linear neural networks offers a valuable simplified setting to understand fundamental learning dynamics. Linearity allows for analytical tractability, enabling the derivation of exact solutions and the exploration of implicit biases. These models reveal crucial insights into how initialization, learning rates, and optimization algorithms shape the learning trajectory, often exhibiting distinct lazy and rich regimes. The lazy regime, characterized by minimal parameter updates, is well understood in the context of kernel methods. However, the rich regime, showcasing significant feature learning and improved generalization, is less analytically tractable but demonstrably crucial to deep learning success. Comparing and contrasting these regimes in the context of linear networks provides a foundation for understanding the complex interplay between architecture, optimization, and data in more realistic nonlinear models. Analyzing conserved quantities and the evolution of the Neural Tangent Kernel (NTK) within the linear framework are key approaches to uncover these insights and provide significant support to the study of more complex, nonlinear systems. Further research in this area seeks to refine the definition of the rich regime in various network architectures, understand its inductive biases, and leverage its properties to enhance deep learning efficiency.
Nonlinear Nets#
In exploring the dynamics of nonlinear neural networks, a significant challenge arises from the intricate interplay between activation functions and the resulting non-convexity of the loss landscape. Unlike linear networks where exact solutions are often attainable, nonlinear systems typically require approximation methods or focus on specific network architectures and initialization schemes. Exact solutions are difficult to obtain and often limited to highly simplified models. A crucial aspect involves understanding how unbalanced initializations, promoting differing learning speeds across layers, can affect the feature learning regime. This asymmetry contrasts with the balanced initialization typically assumed in existing theoretical studies. Investigating how unbalanced initializations impact the conserved quantities that govern learning trajectories in parameter and function space is essential. The influence of activation functions, particularly their piecewise linear nature, on the geometric structure of the learning dynamics remains a key area of exploration, as it affects the transition between lazy and rich learning regimes. Further research should focus on developing analytical methods for analyzing finite-width nonlinear networks with more complex architectures, and on linking theoretical understanding to experimental observations in real-world applications.
Future work#
The paper’s “Future work” section implicitly suggests several crucial research directions. Extending the theoretical framework to deeper, nonlinear networks is paramount, as the current analysis is limited to shallow architectures. This requires tackling the complex interplay of activations and layer interactions that significantly complicates analysis. Furthermore, incorporating the stochasticity and discretization effects of SGD is vital for bridging the gap between theoretical models and practical implementations. Investigating how unbalanced initializations influence various inductive biases, generalization properties, and the learning dynamics of features warrants further exploration. Finally, connecting these findings to the broader context of emergent phenomena, such as grokking and the potential for leveraging the studied dynamics to improve training efficiency, interpretability, and generalization capabilities across diverse applications, remains a promising avenue for future research.
More visual insights#
More on figures
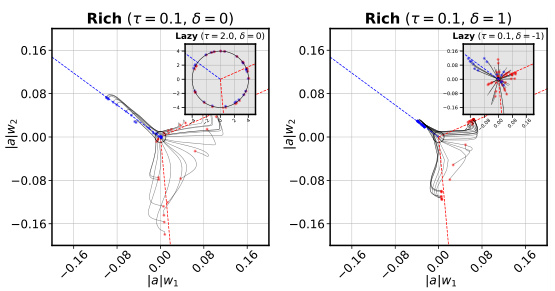
This figure demonstrates how unbalanced initializations affect the learning regime of a two-layer neural network. Panel (a) shows training trajectories for different overall and relative scales, highlighting how upstream initializations lead to faster learning and better alignment with a teacher network. Panel (b) shows a complex phase portrait of learning regimes in parameter space, illustrating the transition from lazy to rich learning driven by overall scale and the directionality of relative scale (upstream vs. downstream).
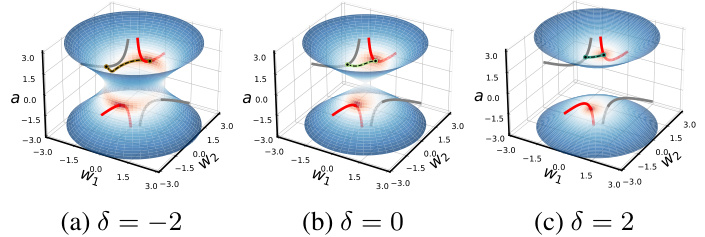
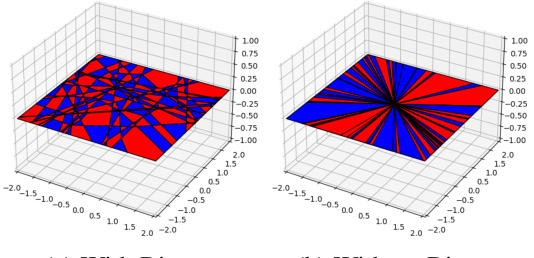
This figure shows how the conserved quantity delta (δ) influences the geometry of the training trajectory in parameter space for a two-layer single-neuron linear network. The conserved quantity δ = nwa² – Na||w||2 constrains the trajectory to different shapes depending on its value: - δ < 0 (Downstream): The trajectory is constrained to a one-sheeted hyperboloid. - δ = 0 (Balanced): The trajectory follows a double cone shape. - δ > 0 (Upstream): The trajectory is constrained to a two-sheeted hyperboloid. The figure illustrates these trajectories for three different initializations (a0, w0) that have the same product (a0*w0), highlighting how the conserved quantity δ shapes the geometry of the optimization landscape.
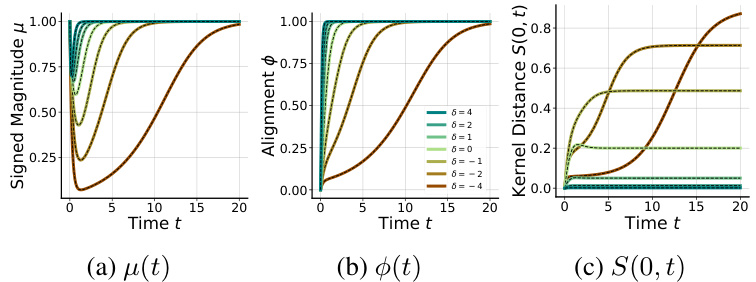
This figure shows the comparison between theoretical predictions and gradient flow simulations for a single hidden neuron model across different values of delta (δ). The metrics plotted are the signed magnitude μ, alignment φ, and kernel distance S(0, t). The results demonstrate distinct learning dynamics across different δ regimes, showcasing lazy, rich, and delayed rich learning behaviors.
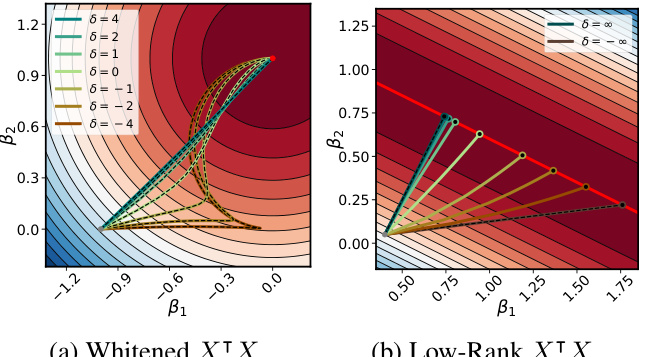
This figure shows how the conserved quantity δ influences the learning trajectories in function space. The left panel shows the trajectories for a whitened input matrix (XTX = I), where exact solutions can be derived. The right panel shows the trajectories for a low-rank input matrix, where exact solutions are only possible in the limit of δ approaching positive or negative infinity. Different initializations (upstream, downstream, and balanced) lead to distinct learning behaviors.
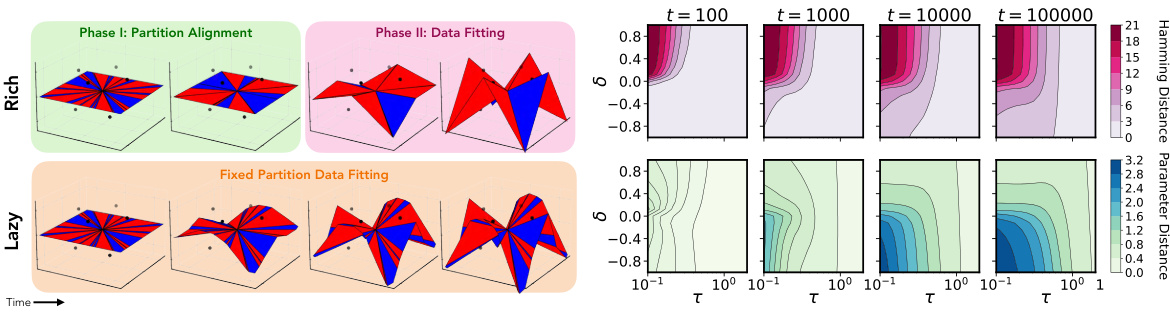
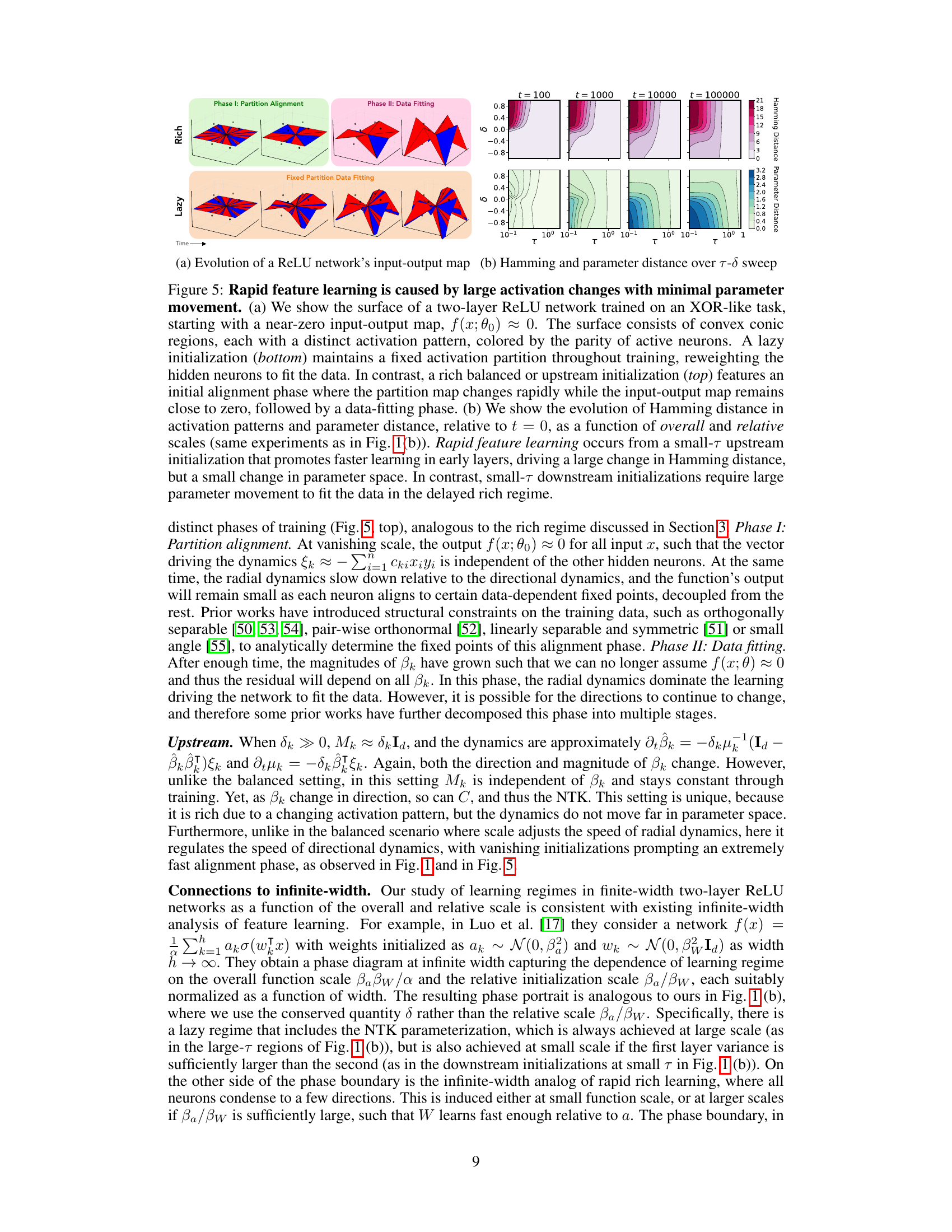
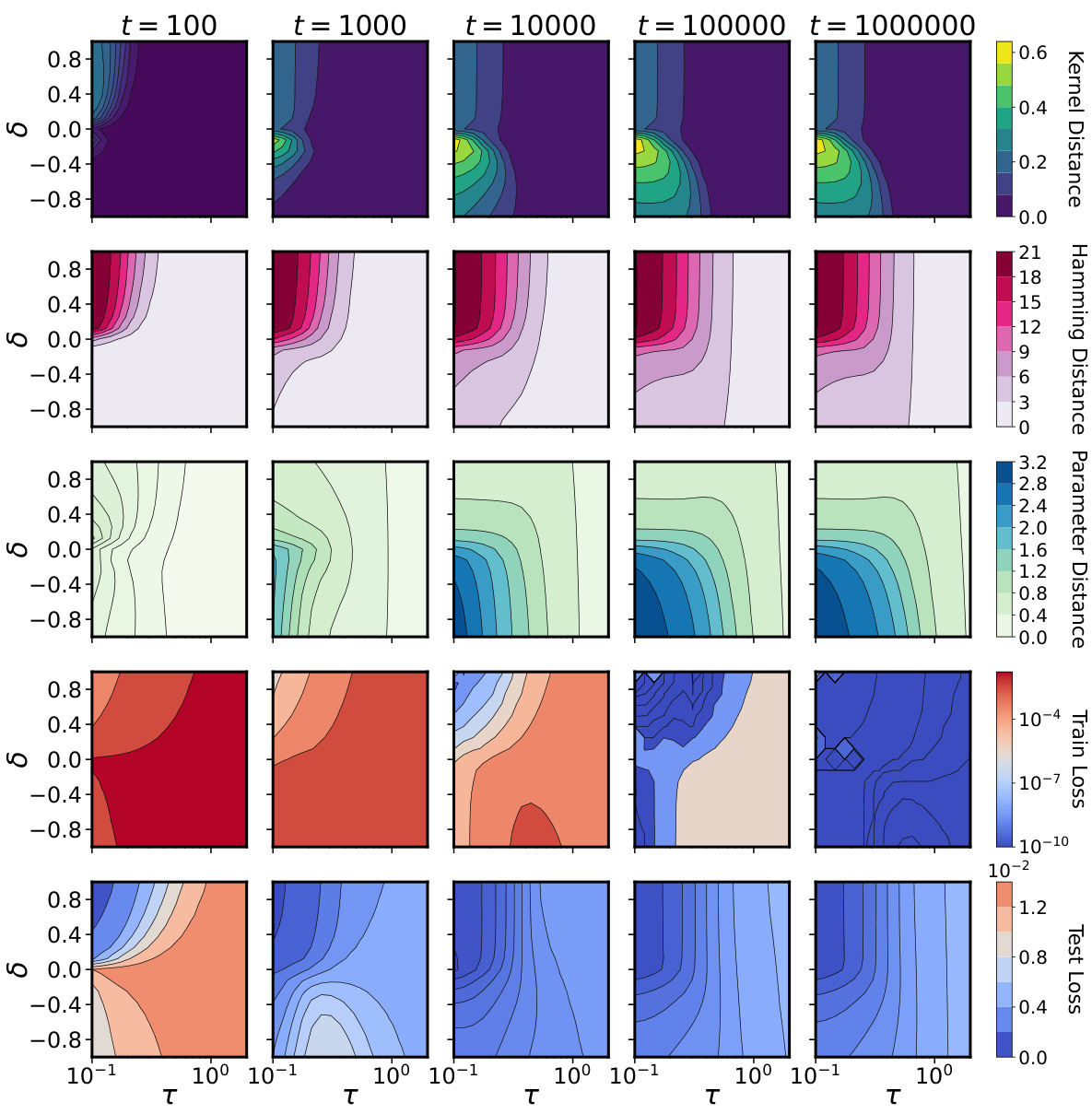
This figure demonstrates the difference between lazy and rich learning regimes in a two-layer ReLU network trained on an XOR-like dataset. Panel (a) visually shows how the input-output map’s surface changes over time, revealing different activation patterns. Lazy learning retains the same activation pattern, while rich learning shows dynamic changes in activation patterns. Panel (b) quantitatively supports these observations by showing that rich learning involves large changes in activation patterns (Hamming distance) with only small changes in parameters, while lazy learning shows smaller changes in both.
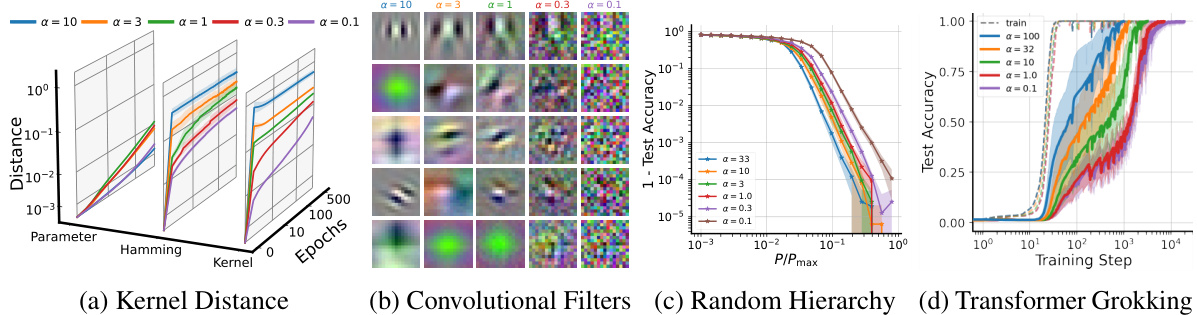
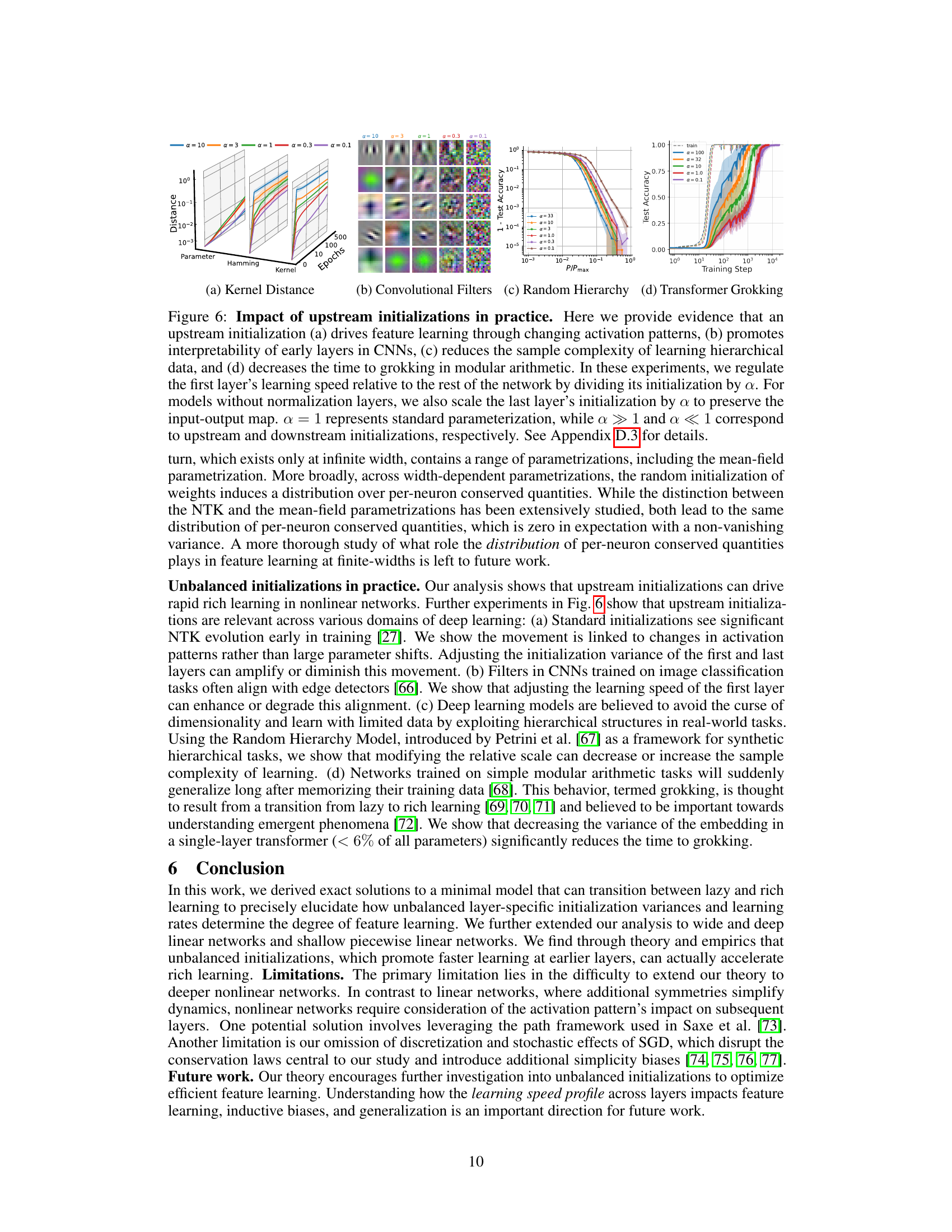
This figure shows experimental results supporting the claim that upstream initializations (where the first layer learns faster than subsequent layers) improve feature learning in various deep learning models. Subfigure (a) shows kernel distance, measuring the change in the model’s learned kernel, demonstrating that upstream initialization leads to more significant changes. Subfigure (b) presents convolutional filter visualizations, showing that upstream initialization leads to simpler, more interpretable filters in the early layers of a CNN. Subfigure (c) illustrates that upstream initialization reduces the sample complexity needed to learn hierarchical data, while subfigure (d) shows that it reduces the time until successful generalization is achieved (a phenomenon known as ‘grokking’).
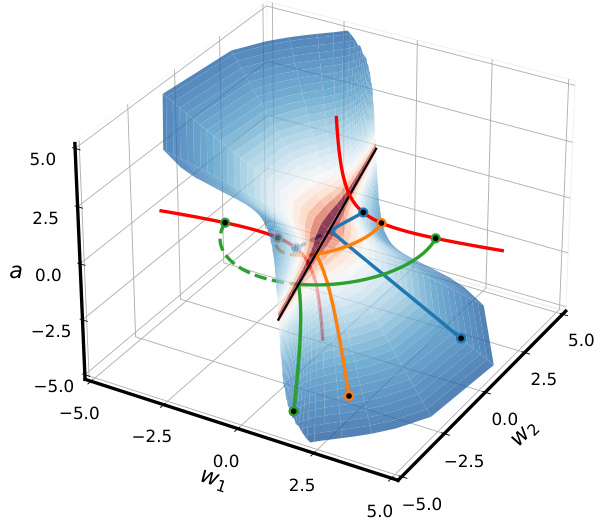
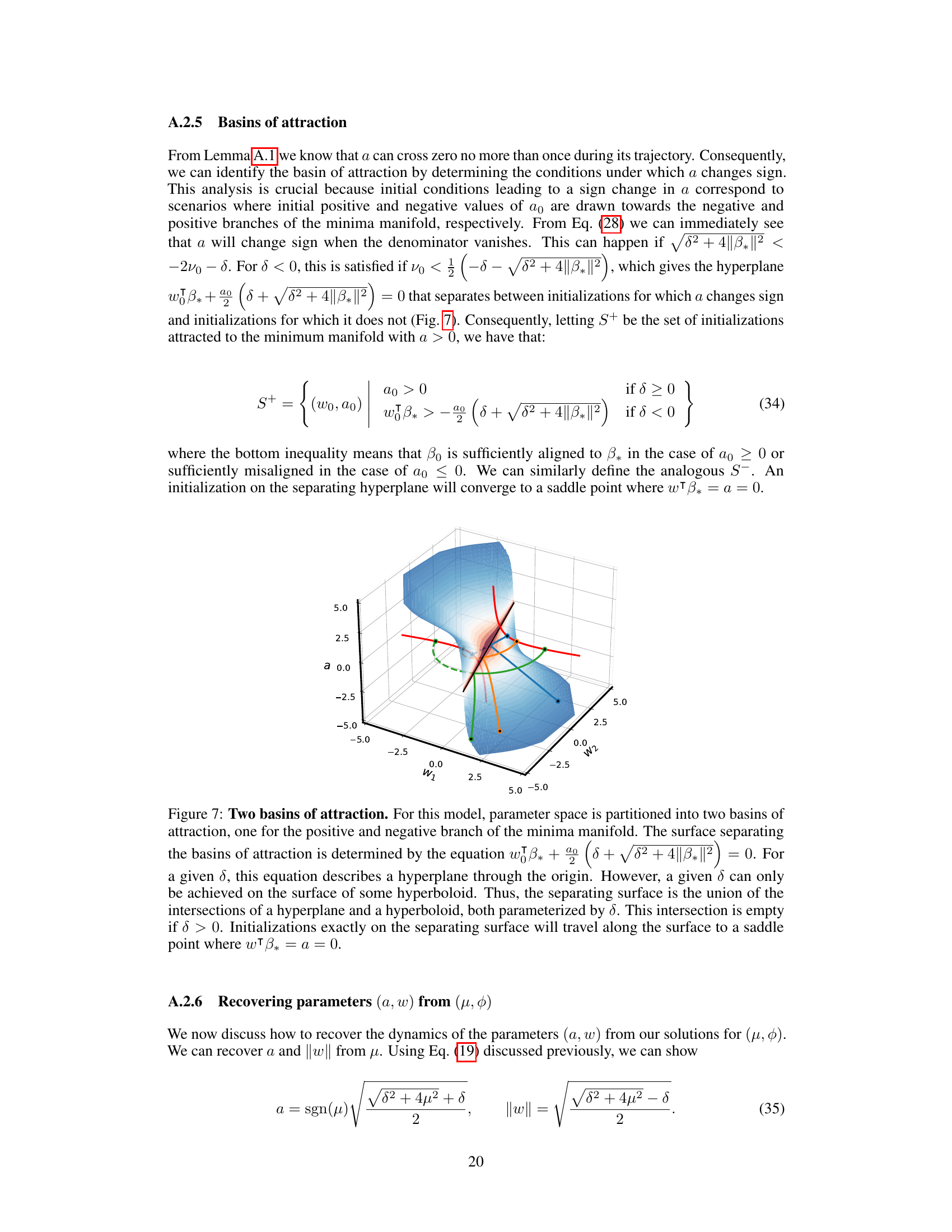
This figure shows how the conserved quantity delta (δ) influences the geometry of the training trajectory in parameter space. Different values of δ correspond to different geometric shapes (hyperboloids or cones), each constraining the learning dynamics to specific regions. The color-coding of the surface indicates the training loss at different points in parameter space, showing how different initializations and trajectories lead to varying levels of loss. The figure visually represents the transition between lazy and rich learning regimes by showing how the geometry of the trajectory changes based on the initial conditions. This is a key illustration of how the conserved quantity affects the training dynamics.
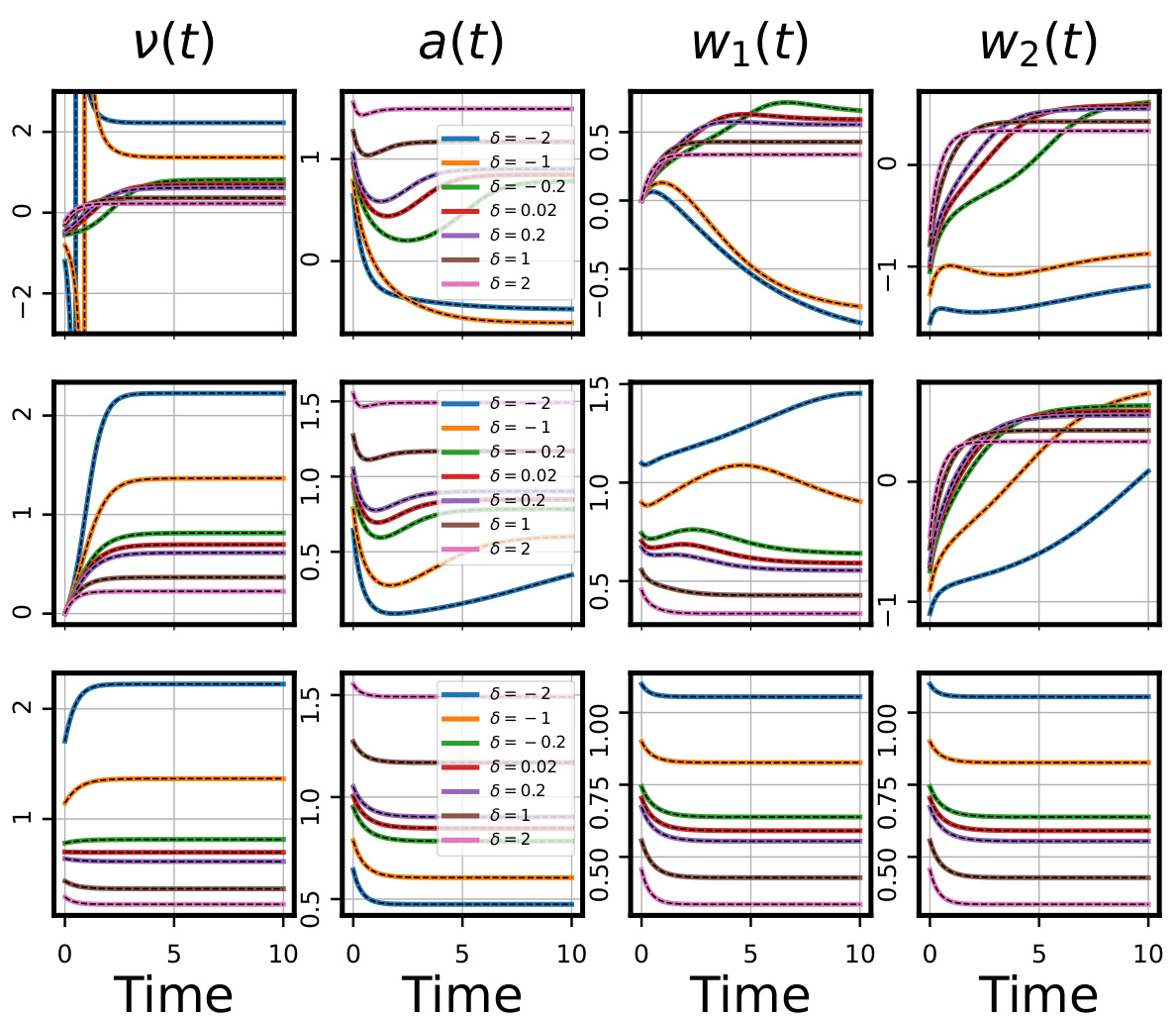
This figure shows the comparison between theoretical predictions and gradient flow simulations for three key metrics (μ, φ, and S(0,t)). The dynamics of these metrics are shown for different values of δ (relative scale), which determines the learning regime (lazy, rich, or delayed rich). Upstream initializations (δ>0) show minimal changes in μ, rapid alignment in φ, and S remains near zero (lazy). Balanced initializations (δ=0) exhibit significant changes in both μ and φ, and S quickly increases (rich). Downstream initializations (δ<0) initially show a rapid decrease in μ, followed by slow increases in both μ and φ, and a delayed increase in S (delayed rich).
This figure shows that rapid feature learning is driven by large changes in the activation patterns with minimal parameter changes. Two-layer ReLU networks are trained on an XOR-like task, starting from an almost-zero input-output map. The top row shows the impact of a balanced or upstream initialization; an initial rapid change in activation patterns with minimal changes to the input-output map, followed by a data-fitting phase. The bottom row illustrates a lazy initialization, where the activation partition remains static throughout training, and the network simply reweights the neurons to fit the data. The right panel (b) further quantifies this by plotting the Hamming distance (changes in activation patterns) and parameter distance as a function of overall and relative scales, demonstrating that unbalanced initializations, especially upstream, lead to fast rich learning.
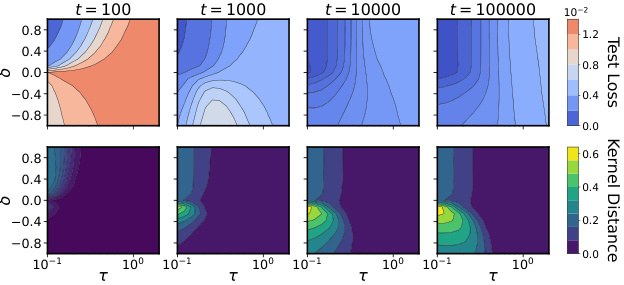
This figure demonstrates the impact of unbalanced initializations on the learning dynamics of a two-layer neural network. Panel (a) shows how different overall scales and relative scales between layers affect the training trajectories, leading to either lazy or rich learning regimes. Panel (b) illustrates the relationship between overall scale, relative scale, test loss, and kernel distance, revealing that a small overall scale and large relative scale (upstream initialization) lead to rapid rich learning and good generalization.
This figure shows experimental results supporting the claim that upstream initialization promotes rapid feature learning. It demonstrates the impact of unbalanced initializations on four different aspects: feature learning via activation pattern changes, interpretability of early convolutional layers, sample complexity in hierarchical data learning, and the speed of ‘grokking’ in modular arithmetic. In all cases, the effect is achieved by modifying the initialization variance of early layers relative to later ones.
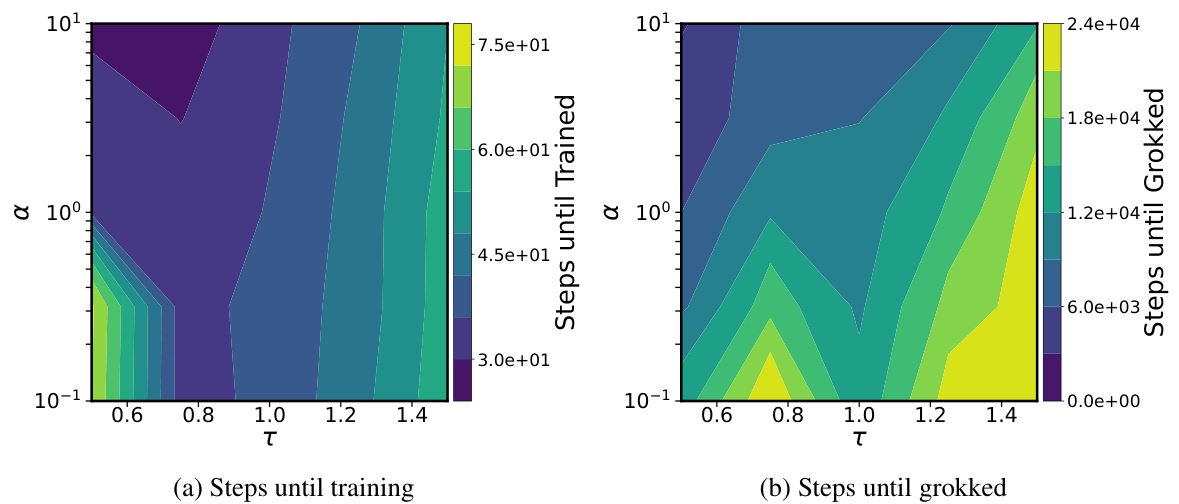
This figure demonstrates the impact of upstream initializations on various aspects of deep learning. It shows that upstream initializations (where the first layer learns faster than subsequent layers) lead to faster feature learning, improved interpretability of early layers in convolutional neural networks (CNNs), reduced sample complexity in learning hierarchical data, and faster ‘grokking’ (sudden generalization) in modular arithmetic tasks. The experiments involve scaling the initialization of the first (and last) layer to control the relative learning speed. Subfigures illustrate these impacts using different metrics: kernel distance, convolutional filter visualizations, random hierarchy model results, and transformer grokking results.
Full paper#