↗ OpenReview ↗ NeurIPS Proc. ↗ Chat
TL;DR#
Multi-agent learning, especially no-regret learning, is well-understood in potential games where players share common interests. However, the dynamics remain largely unknown in harmonic games where interests conflict. This paper focuses on generalized harmonic games and investigates the convergence properties of the widely used Follow-the-Regularized-Leader (FTRL) algorithm. The authors reveal that standard FTRL methods can fail to converge, potentially trapping players in cycles.
This work addresses these limitations by introducing a novel algorithm called extrapolated FTRL. This enhanced method incorporates an extrapolation step, including optimistic and mirror-prox variants, and is shown to converge to Nash equilibrium from any starting point, guaranteeing at most constant regret. The analysis provides insights into continuous and discrete-time dynamics, unifying existing work on zero-sum games and extending the knowledge to the broader class of harmonic games. This highlights the fundamental distinction and connection between potential and harmonic games, from both a strategic and dynamic viewpoint.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in game theory, multi-agent systems, and machine learning because it unveils the dynamics of no-regret learning in harmonic games, a class of games with conflicting interests previously under-explored. The findings challenge existing assumptions, highlighting the limitations of standard no-regret learning algorithms and providing a novel extrapolated FTRL algorithm that guarantees convergence to Nash equilibrium. This opens avenues for designing more effective and robust learning algorithms in complex strategic settings.
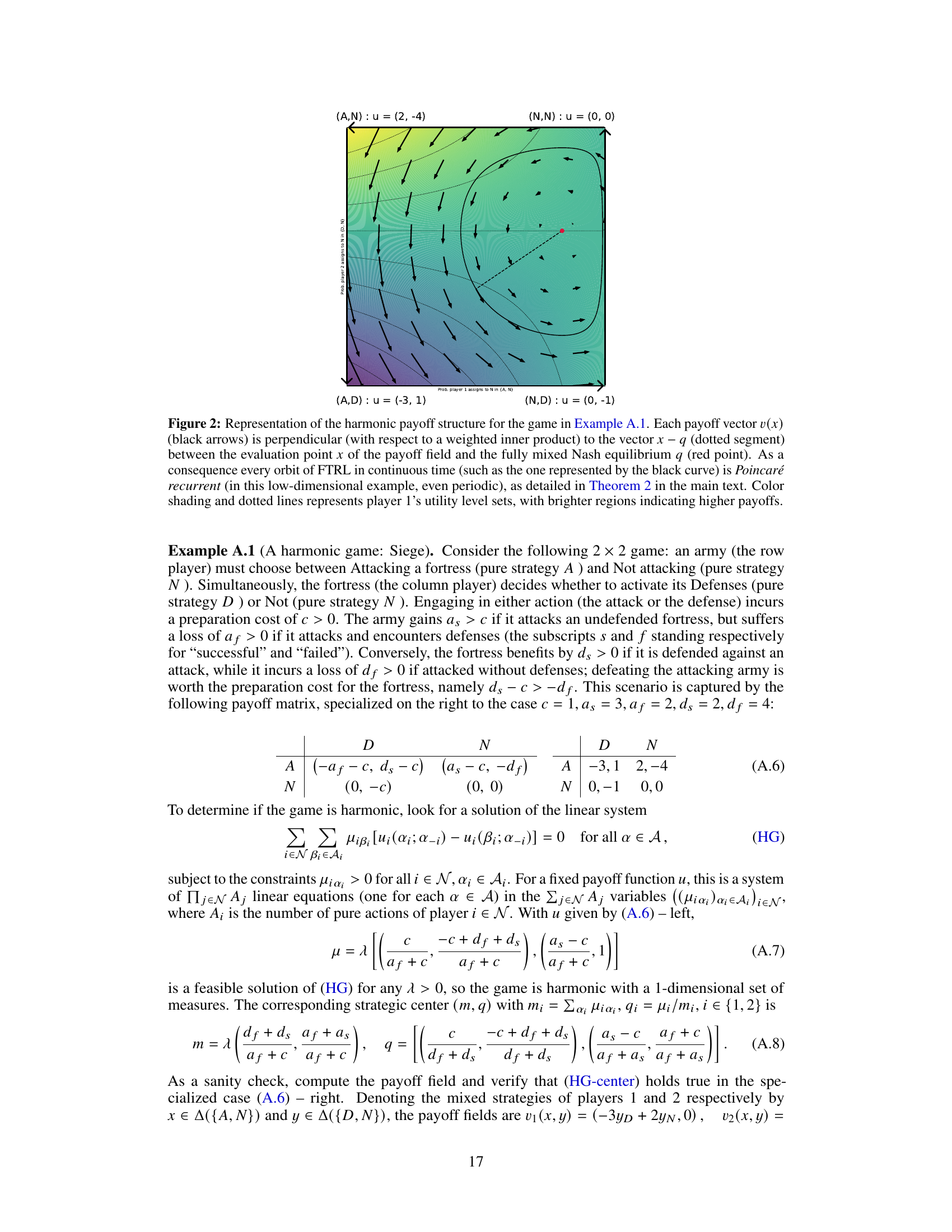
Visual Insights#
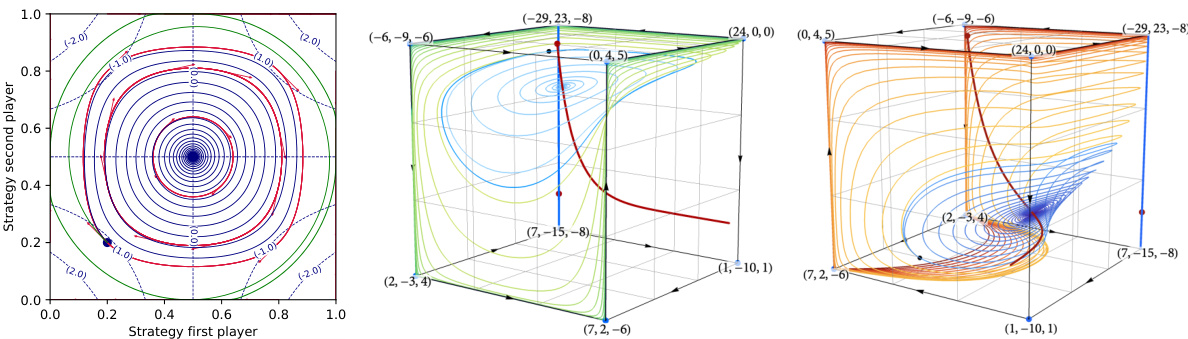
This figure compares the performance of three different FTRL algorithms in harmonic games. The left panel shows the trajectories of the standard FTRL, the extrapolated FTRL (FTRL+), and the continuous-time version of FTRL in the Matching Pennies game. The center and right panels illustrate the trajectories for a 2x2x2 harmonic game from different perspectives. The figure demonstrates that the standard FTRL algorithm diverges, while FTRL+ converges to the Nash equilibrium. The continuous-time FTRL is shown to be recurrent (periodic).
Full paper#