↗ OpenReview ↗ NeurIPS Proc. ↗ Chat
TL;DR#
Many real-world applications of Bayesian Optimization (BO) involve human experts who provide feedback to guide the search. However, existing methods often struggle with noisy or unreliable expert advice and lack theoretical guarantees about their performance. This paper introduces COBOL, a new algorithm that addresses these limitations.
COBOL uses a principled approach where experts provide binary accept/reject recommendations on proposed query points. The algorithm incorporates a data-driven trust mechanism that dynamically adjusts the weight assigned to expert feedback, ensuring that even if the expert’s advice is unreliable or adversarial, the algorithm’s performance is never worse than a standard BO algorithm without expert input. The authors prove two key guarantees: a ‘handover guarantee’, meaning that the number of expert labels required asymptotically converges to zero, and a ’no-harm guarantee’, meaning that the convergence rate is never worse than when not using expert advice. Experiments on both synthetic and real-world (battery design) tasks demonstrate that COBOL outperforms existing baselines and maintains robustness even under noisy or adversarial labeling.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in Bayesian Optimization and human-in-the-loop machine learning. It addresses the critical need for robust and efficient methods that leverage human expertise effectively, offering theoretical guarantees and real-world applicability. The data-driven trust mechanism is a significant methodological advance, offering insights into human-AI collaboration. The results open exciting avenues for future research in handling unreliable human feedback and creating more robust and efficient optimization algorithms.
Visual Insights#

This figure illustrates the framework for collaboration between a Bayesian Optimization (BO) algorithm and human experts. The BO algorithm proposes a candidate point. The expert then provides a binary label (‘accept’ or ‘reject’). If the expert is ‘uncertain’, the algorithm performs a cross-check of the expert’s reliability; if ‘confident’, it proceeds directly. This process allows the BO algorithm to efficiently incorporate expert knowledge while maintaining robustness against potentially unreliable expert advice.
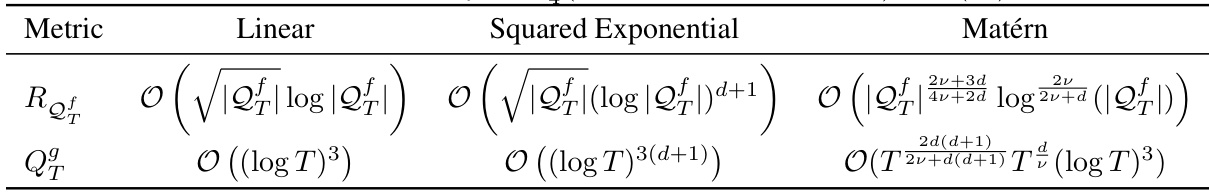
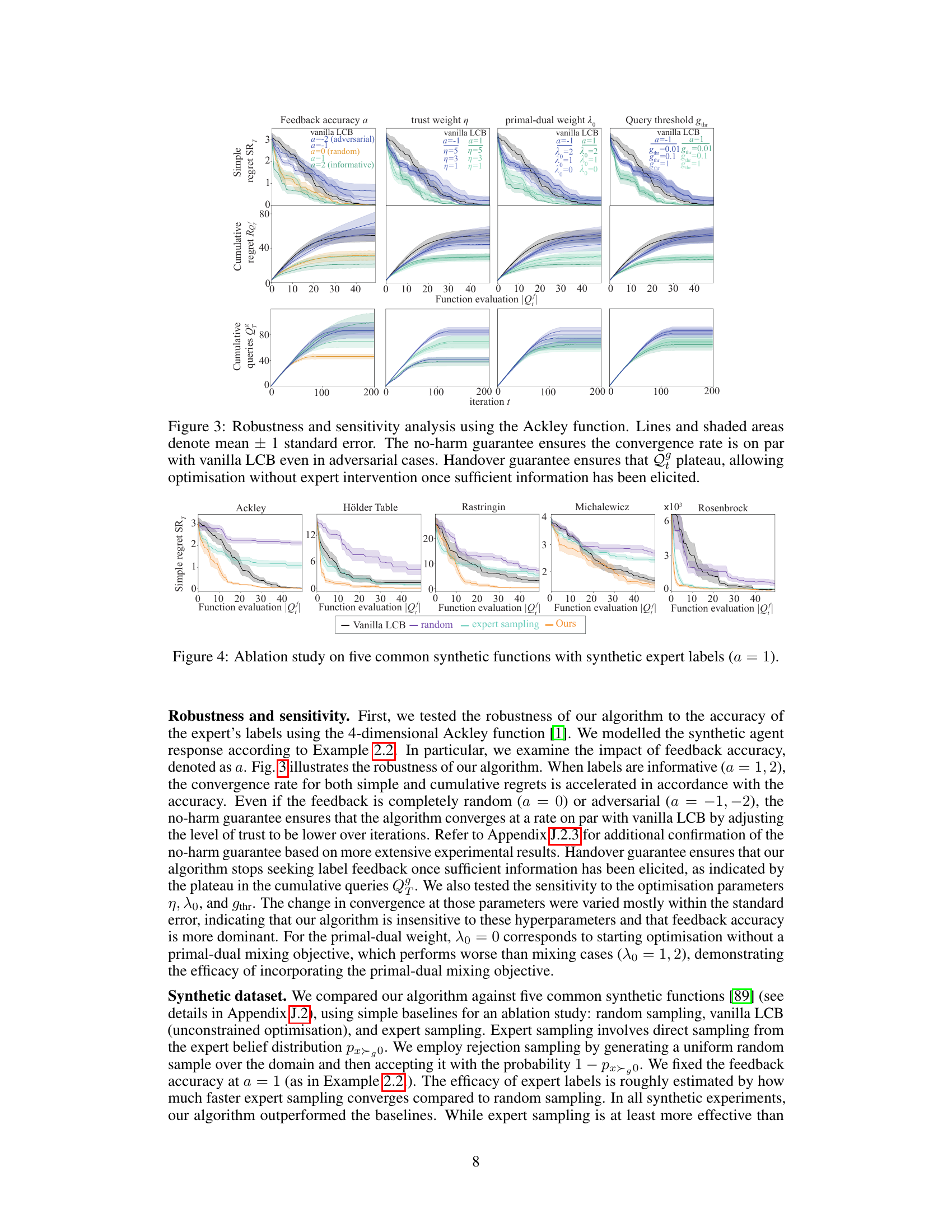
This table presents the theoretical upper bounds on cumulative regret (RQf) and cumulative number of expert queries (QgT) for different kernel functions used in the Bayesian Optimization algorithm. The bounds depend on the kernel type (Linear, Squared Exponential, Matérn), the dimension (d) of the problem, and the number of iterations (T). The Matérn kernel bound additionally depends on the smoothness parameter (v). The table shows how the theoretical convergence rates vary based on the kernel choice, highlighting the trade-offs involved.
In-depth insights#
Human-AI Collab BO#
The field of Human-AI Collaborative Bayesian Optimization (BO) explores the synergy between human expertise and algorithmic optimization. A core challenge lies in effectively integrating human feedback, which can be qualitative, costly, and potentially unreliable. Early approaches often assumed near-oracle human knowledge, leading to algorithms vulnerable to inaccurate advice. More recent methods, like the one described in this paper, tackle this by introducing novel theoretical guarantees: no-harm guarantees ensure performance is never worse than using BO alone, even with adversarial advice, while handover guarantees ensure that human involvement asymptotically decreases as the optimization progresses. The design of the human interaction method is also critical; minimizing interaction is desirable, but eliciting sufficiently informative and reliable data is a key challenge. Data-driven trust level adjustments rather than relying on user-defined functions provide more robustness. The study’s empirical evaluations, particularly on real-world battery design, highlight the practical benefits and resilience of this principled approach, showcasing potential for fast convergence even with less reliable human input.
Handover Guarantee#
The concept of a ‘Handover Guarantee’ in the context of human-in-the-loop Bayesian Optimization is crucial for efficient collaboration. It speaks to the algorithm’s ability to gradually reduce reliance on human expert input as the optimization progresses. Initially, the algorithm heavily leverages expert feedback, likely requiring multiple labels per query point. However, as the algorithm gathers more data and its confidence in the surrogate model increases, the frequency of requesting expert labels decreases asymptotically. This is extremely important because expert labels are often expensive and time-consuming to obtain. The ‘handover guarantee’ ensures that the algorithm doesn’t become overly reliant on potentially unreliable expert advice, gracefully transitioning to autonomous operation as it becomes more certain about the search space. A sublinear bound on the cumulative number of expert labels provides a formal guarantee on this efficient handover, which is a significant theoretical contribution.
No-Harm Guarantee#
The “No-Harm Guarantee” in this research paper is a crucial theoretical contribution, ensuring that incorporating human expert advice into the Bayesian Optimization (BO) process never performs worse than standard BO without expert input, even if the expert advice is completely unreliable or even adversarial. This robust guarantee is achieved through a data-driven trust level adjustment mechanism, unlike existing methods relying on hand-tuned parameters. The method dynamically adjusts its reliance on expert labels based on observed data, preventing over-reliance on potentially erroneous advice. This adaptive trust is key to maintaining performance consistency, making the algorithm suitable for real-world scenarios where expert knowledge may be incomplete, inconsistent, or simply wrong. The guarantee’s significance is highlighted by its applicability to scientific applications where expert guidance is vital yet often uncertain; it fosters trust in human-AI collaborations within BO by providing a safety net for potentially unreliable human input. The no-harm guarantee, therefore, represents a significant advancement, enhancing the robustness and reliability of expert-augmented BO, making it a more practical tool for real-world problem-solving.
Real-World Robustness#
The concept of “Real-World Robustness” in the context of a research paper likely explores the algorithm’s performance and reliability when applied to real-world scenarios, which are inherently noisy and complex. A key aspect would be evaluating its resilience to erroneous or incomplete data, which is common in real-world applications where human experts might provide subjective or unreliable input. The analysis would likely examine how the algorithm adapts and maintains accuracy when the input data deviates from idealized assumptions. This may involve testing it under various conditions such as noisy labels, adversarial input, or missing information to demonstrate how well it generalizes beyond laboratory settings. Demonstrating real-world robustness is crucial for establishing practical viability and trustworthiness, particularly when human-in-the-loop optimization is involved. The findings should highlight the algorithm’s ability to converge on accurate solutions despite the presence of real-world imperfections.
Future Extensions#
The “Future Extensions” section of this research paper presents exciting avenues for enhancing the human-in-the-loop Bayesian optimization framework. Addressing the time-varying nature of human expertise is crucial, suggesting dynamic models that adapt to evolving knowledge and potentially incorporating techniques like windowing to manage outdated information. Further investigation into alternative feedback mechanisms beyond binary labels, including pairwise comparisons, ranking, or belief functions, could broaden applicability and better align with human preferences. Exploring adaptive trust mechanisms that automatically adjust the level of confidence placed in expert advice based on data-driven evidence is a significant area for development. Finally, the paper suggests extensions to handle high-dimensional problems and multiple expert scenarios, improving scalability and leveraging the collective wisdom of multiple experts. These proposed extensions are not only theoretically intriguing but also practically relevant, aiming to further optimize the collaborative human-AI optimization process.
More visual insights#
More on figures
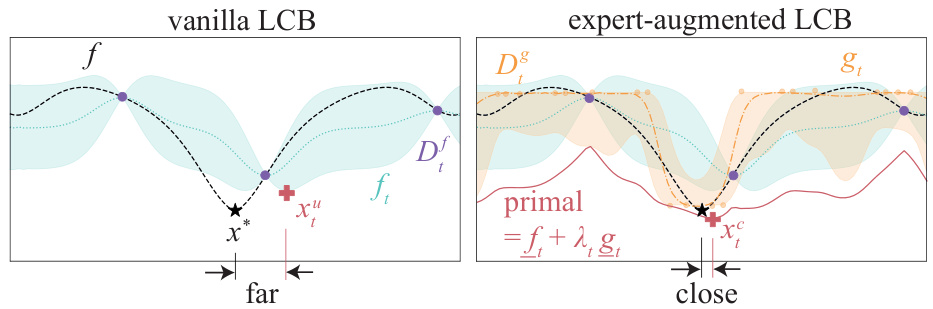
This figure compares the vanilla Lower Confidence Bound (LCB) and the expert-augmented LCB acquisition functions. The vanilla LCB selects a point (xu) that is far from the global minimum (x*). The expert-augmented LCB, however, incorporates expert feedback (Di) to guide the selection of a point (xf) closer to the global minimum by combining the surrogate objective function (ft) and the expert belief function (gt) using a primal-dual approach with a weighting factor (λt). This demonstrates how the integration of expert knowledge improves the efficiency of the Bayesian Optimization (BO) process.
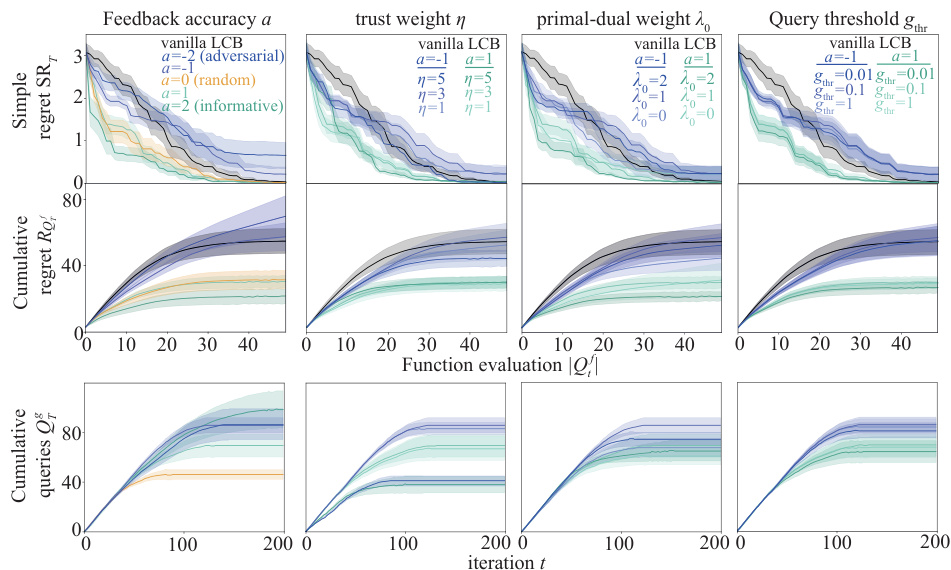
This figure demonstrates the robustness and sensitivity of the proposed algorithm (COBOL) using the Ackley function. The plots show the simple regret, cumulative regret, and cumulative queries for different scenarios, manipulating the accuracy of expert feedback (a), the trust weight (η), the primal-dual weight (λ0), and the query threshold (gthr). The no-harm guarantee is evidenced by the convergence rate remaining comparable to the vanilla LCB even with adversarial expert advice (a=-2, -1). The handover guarantee is shown by the plateauing of the cumulative queries, demonstrating that COBOL reduces the reliance on expert labels over time.
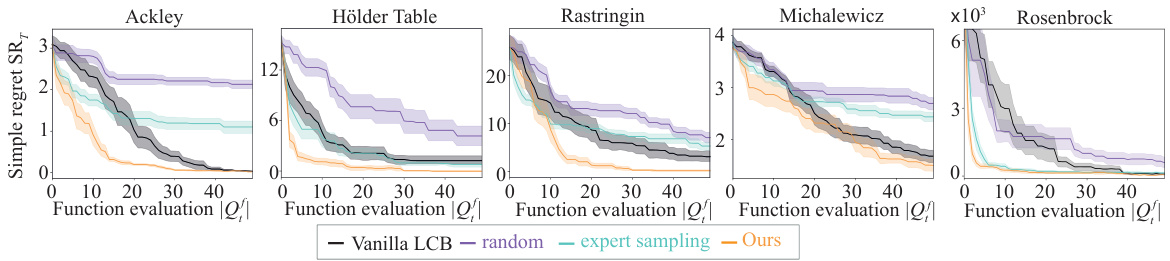
This figure presents a comprehensive comparison of five different algorithms across five common synthetic benchmark functions. The algorithms being compared are Vanilla LCB, random sampling, expert sampling, and the proposed COBOL algorithm. For each function, the figure displays four subplots visualizing simple regret, cumulative regret, overhead (computational time), and cumulative expert queries. Shaded areas around the lines represent standard error. The results visually demonstrate the performance of the proposed COBOL algorithm in comparison to baselines, highlighting its efficiency and robustness in various scenarios.
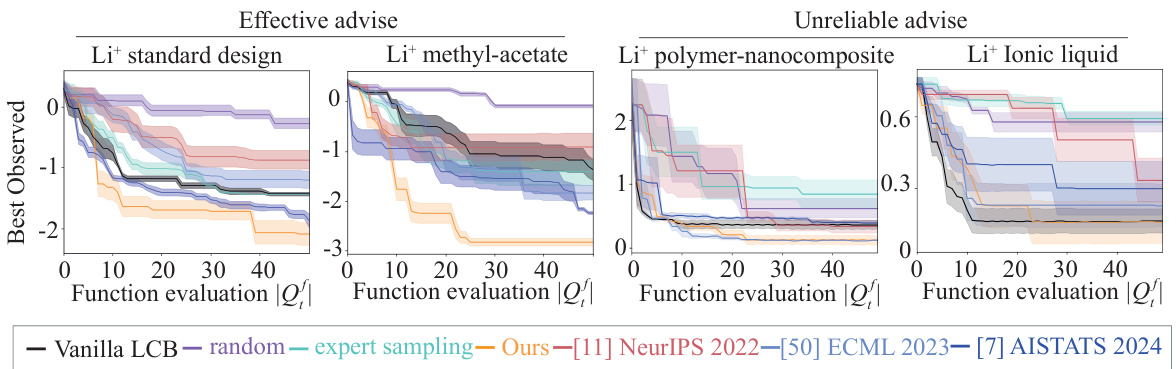
This figure presents the results of real-world experiments on four different lithium-ion battery designs, comparing the performance of the proposed COBOL algorithm against several baselines. The baselines include vanilla LCB (which doesn’t use human expertise), random sampling, and expert sampling (where experts select the next point to evaluate). The four battery types represent a range of complexities and expert knowledge levels: Li+ standard design (well-understood system), Li+ methyl-acetate (slightly modified system), Li+ polymer-nanocomposite (newer material), and Li+ Ionic liquid (newer material). The x-axis represents the number of function evaluations (i.e., experiments conducted), and the y-axis shows the best observed value of the objective function. The shaded regions represent the standard error.
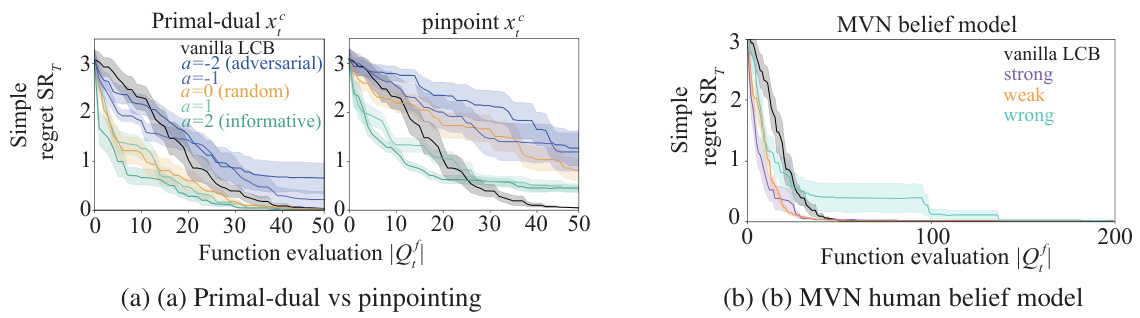
This figure compares the performance of the proposed algorithm using three different forms of human feedback: primal-dual, pinpoint, and MVN belief model. The primal-dual approach uses the algorithm’s acquisition policy, while the pinpoint approach has the human expert directly select the next query point. The MVN belief model represents the human belief function as a multivariate normal distribution. The plots show simple regret versus the number of function evaluations for each feedback method. The results demonstrate that the primal-dual approach generally outperforms the other two methods, especially in later iterations. The pinpoint approach initially performs relatively well but eventually lags behind the primal-dual method. The MVN belief model’s performance varies greatly depending on the strength of the belief provided by the human expert.
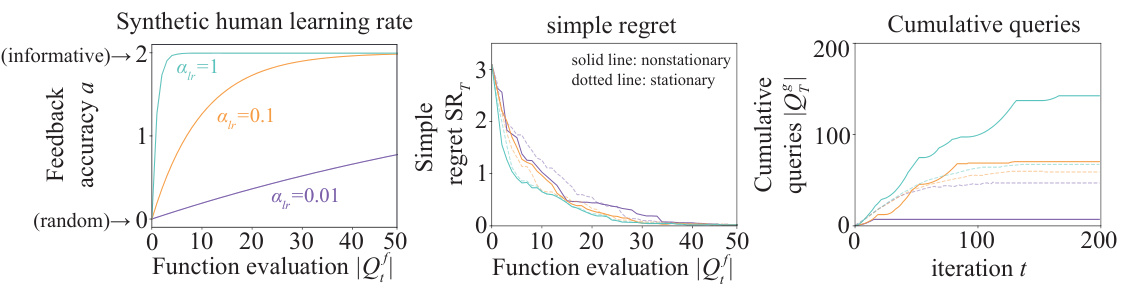
This figure shows the results of an ablation study on the impact of non-stationary human feedback accuracy on the algorithm’s performance. The left panel shows how the feedback accuracy changes over time for different learning rates (αtr). The middle panel displays the simple regret, comparing the performance of the algorithm with non-stationary feedback (solid lines) against the stationary case (dotted lines) across various learning rates. The right panel illustrates the cumulative number of queries to the human expert over time. The results demonstrate the algorithm’s robustness to changing expert accuracy, even when the accuracy is low or non-stationary.
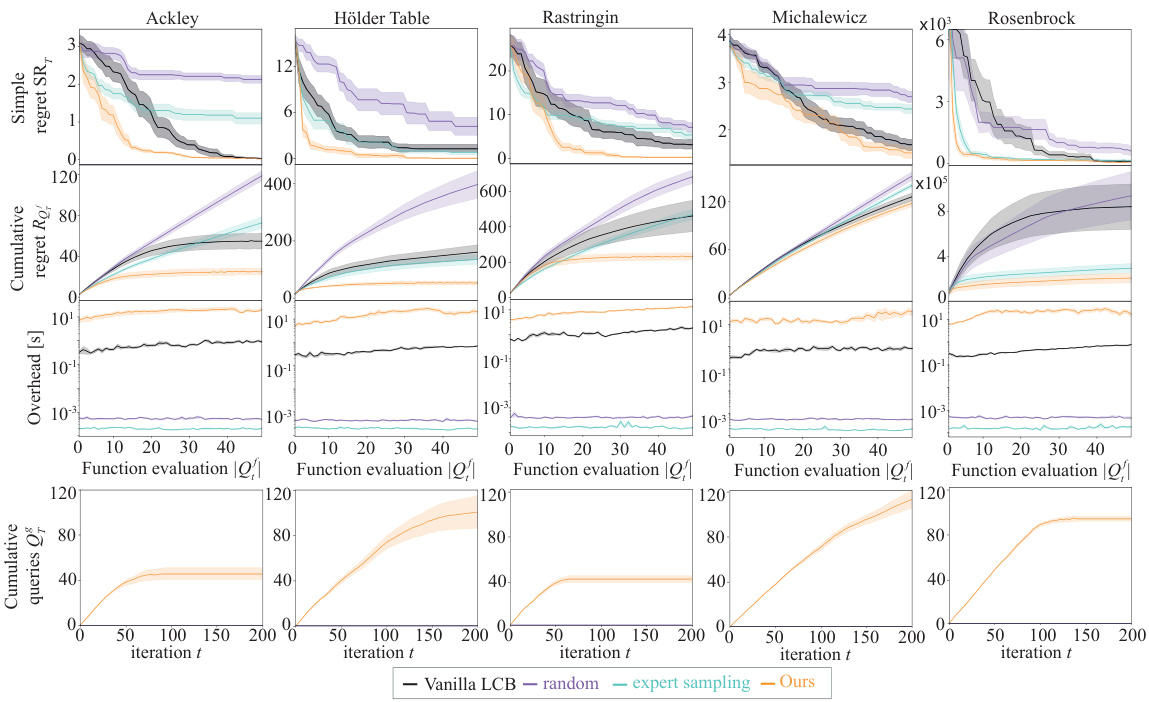
This figure presents a comprehensive set of experimental results obtained from synthetic experiments using five different benchmark functions (Ackley, Holder Table, Rastrigin, Michalewicz, and Rosenbrock). Each subplot represents a different function and shows four key metrics: simple regret (SRₜ), cumulative regret (Rₜ), overhead (in seconds), and cumulative queries (Qₜ). The x-axis shows the number of function evaluations, while the y-axes represent the values of the respective metrics. The results for four different methods are presented and compared: Vanilla LCB, random sampling, expert sampling, and the proposed COBOL algorithm. The shaded areas represent the standard errors.
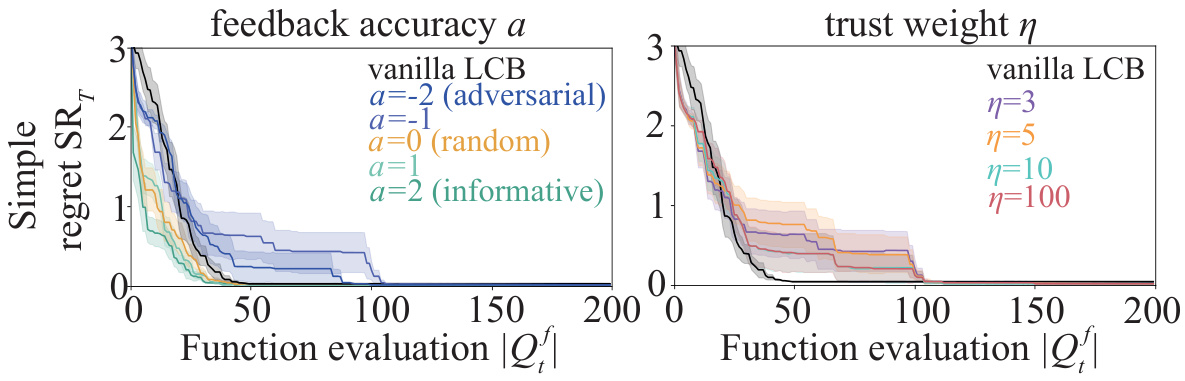
This figure shows the results of robustness and sensitivity analysis using the Ackley function. The no-harm guarantee is demonstrated by the convergence rate being on par with the vanilla lower confidence bound (LCB) even when the expert advice is adversarial. The handover guarantee is demonstrated by the plateauing of the cumulative queries to the expert (Qf), indicating that the optimization process can proceed without further expert input once sufficient information has been gathered. The plot includes lines representing the mean and shaded areas representing the standard error.
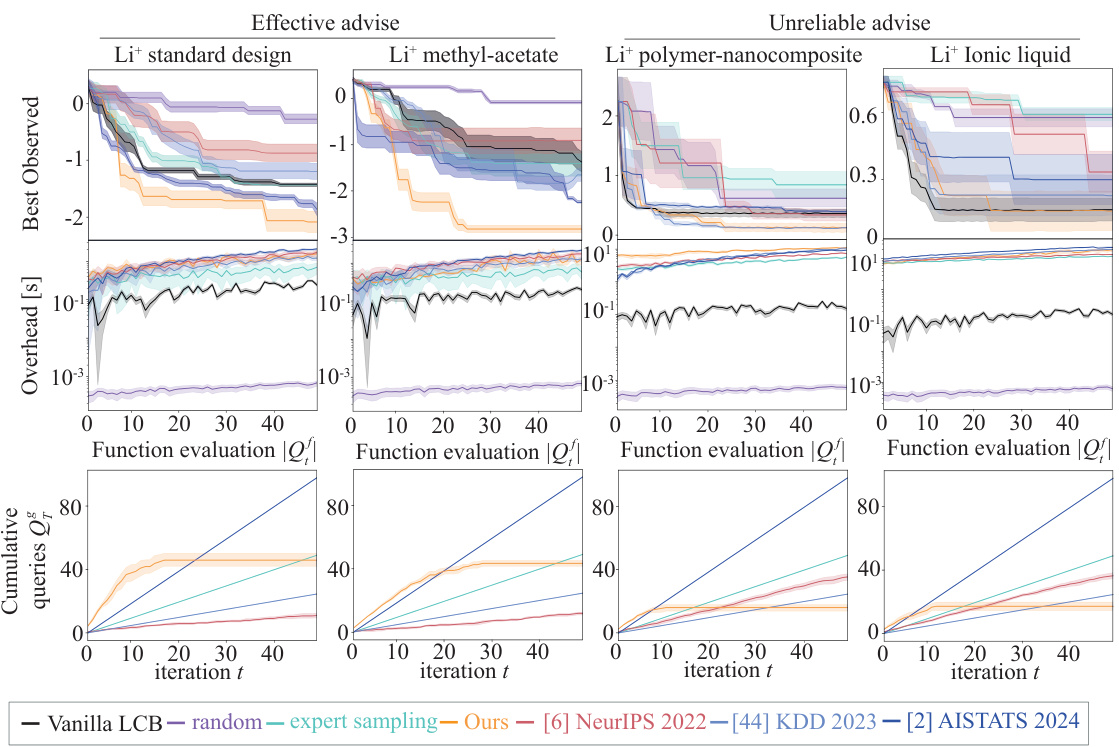
This figure presents the results of real-world experiments conducted with four human experts on four different lithium-ion battery electrolyte systems. The results are shown for four different electrolyte types: Li+ standard design, Li+ methyl-acetate, Li+ polymer-nanocomposite, and Li+ ionic liquid. For each electrolyte type, the figure displays the best observed value, overhead (time to generate the next query location), and cumulative queries. The results are broken down into two groups: ‘Effective advise’ where expert input is reliable and ‘Unreliable advise’ where expert input is less reliable. The comparison includes results for vanilla LCB, random sampling, expert sampling, and the proposed COBOL algorithm. The figure demonstrates the relative performance of the different methods in terms of achieving low regret (error), minimal overhead, and efficient use of expert input.
More on tables

This table compares the proposed algorithm with several existing baseline methods across various criteria such as whether they model human experts, the assumptions they make, and the guarantees they provide (no-harm, handover, etc.). It highlights the unique features of the proposed method, which include considering the no-rankability assumption, providing a continuous domain guarantee, and offering both data-driven trust and handover guarantees.
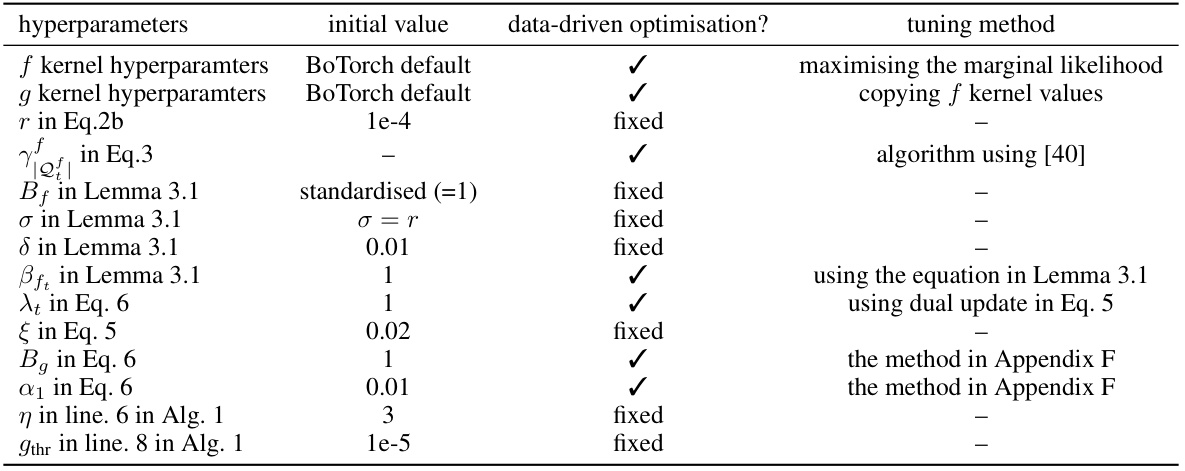
This table lists all hyperparameters used in the paper, their initial values, whether they are tuned using a data-driven approach, and the tuning method used. It provides details for hyperparameters related to the Gaussian processes for both the objective function and the expert belief, regularization terms, confidence bounds, and the primal-dual algorithm. This level of detail is important for reproducibility of the results.
Full paper#