Identifying Causal Effects Under Functional Dependencies

↗ OpenReview ↗ NeurIPS Proc. ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is important because it improves causal effect identification by incorporating functional dependencies, a type of qualitative knowledge often available in real-world scenarios. This leads to more identifiable causal effects and reduces the need for extensive observational data, advancing causal inference methods and their applicability.

Visual Insights

#

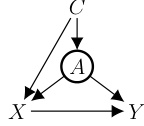
This figure shows a causal graph G with observed variables V = {A, X, Y}. Variable B is circled to indicate that it is a functional variable (meaning its value is deterministically determined by its parents). The arrow from X to Y represents a direct causal effect. The graph is used as an example to discuss causal effect identifiability in the presence of functional dependencies; specifically, whether the causal effect of X on Y can be uniquely determined from the observed data, given the functional dependency of B.

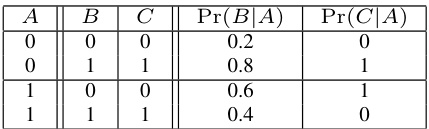
This table shows the conditional probability distributions Pr(B|A) and Pr(C|A) given the parent variable A. The table demonstrates a functional dependency, where variable C is functionally determined by its parent A (Pr(C|A) is deterministic), while variable B is not.

In-depth insights

#

Causal Effect ID

#

Causal Effect ID, in the context of causal inference, is a crucial process aiming to determine if a causal effect can be uniquely computed from observational data and a causal graph. Identifiability is paramount; if an effect isn’t identifiable, estimating it from observational data alone is unreliable, potentially yielding different results depending on the underlying data-generating model. This highlights the importance of algorithms and criteria (like do-calculus or the ID algorithm) designed to assess identifiability. These methods leverage the structure of the causal graph to determine whether the causal effect can be expressed solely in terms of observable distributions. The presence of unobserved variables (latent confounders) significantly complicates identifiability, often rendering otherwise identifiable effects unidentifiable. Further complexities arise with functional dependencies, where one variable is deterministically determined by its parents. Accounting for functional dependencies enhances identifiability assessment, sometimes revealing previously unidentifiable effects. Overall, Causal Effect ID is a critical step in establishing the validity and reliability of causal inferences based on observational studies.

Functional Dep

#

The concept of ‘Functional Dependencies’ in a causal inference context is a significant contribution, refining causal effect identification. It leverages the deterministic nature of certain variables (functionally determined variables) within a causal graph. This knowledge, even without precise functional forms, offers improvements in two key ways: identifiability of previously unidentifiable causal effects and reduction in the number of variables needing observation. The core methodology involves an elimination process that systematically removes functional variables while preserving key causal properties, enabling the use of existing causal identification algorithms with refined constraints. This is particularly relevant when experimental data is scarce or ethically challenging to obtain, shifting reliance to observational data. The theoretical implications are considerable, potentially impacting how we design studies, collect data, and estimate causal effects in diverse domains.

Identifiability

#

Identifiability, in the context of causal inference, is the ability to uniquely determine a causal effect from observational data and a causal graph. The paper delves into improving identifiability by leveraging knowledge of functional dependencies among variables. This means, if some variables are deterministically determined by their parents, identifiability can be enhanced in two key ways: previously unidentifiable effects might become identifiable, and some variables might be excluded from observation without compromising identifiability, reducing data collection needs. The authors introduce new theoretical tools, such as functional elimination and projection, which manipulate the causal graph while preserving crucial properties. These improvements stem from a deeper understanding of the interplay between functional dependencies, positivity assumptions, and the identifiability of causal effects. The core contribution is a more refined framework for evaluating identifiability that considers qualitative knowledge about the system, leading to more efficient and practical causal analysis.

Project-ID Algo

#

The Project-ID algorithm is a two-stage process for identifying causal effects. The first stage, projection, simplifies the causal graph by focusing only on observed variables, creating a new graph where hidden variables are roots with only two children each. This simplification makes the graph amenable to the second stage, the ID algorithm, which provides a sound and complete method for identifying causal effects under specific positivity constraints (assumptions that prevent zero probabilities). However, the algorithm’s reliance on positivity constraints is a limitation, potentially excluding real-world scenarios where such constraints don’t hold. Despite this, Project-ID offers an efficient approach to causal effect identification by reducing the complexity of the causal graph and providing a formal procedure for testing identifiability.

Future Research

#

Future research directions stemming from this work on causal effect identification under functional dependencies could involve exploring more sophisticated positivity constraints that better capture real-world scenarios. Investigating the interplay between functional dependencies and other forms of qualitative knowledge, such as context-specific independence, would be valuable. Furthermore, developing more efficient algorithms for testing functional identifiability, particularly those that don’t rely on existing identifiability algorithms, represents a significant challenge and opportunity. Extending the framework to handle continuous variables and more complex causal structures would broaden its applicability. Finally, applying these insights to real-world problems across various domains, especially those involving ethical considerations, is crucial to demonstrate the practical value of this research and identify new challenges. Developing user-friendly software tools that incorporate these advances in causal inference would facilitate wider adoption and impact.

More visual insights

#

More on figures

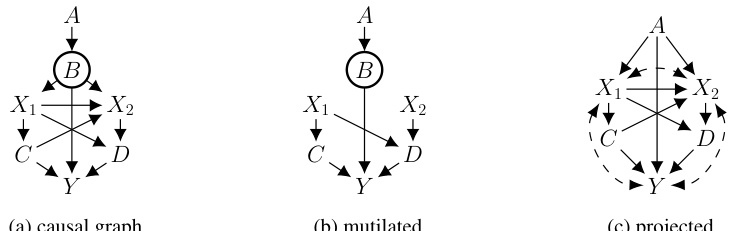
This figure shows an example causal graph adapted from another paper. The graph has both observed and hidden variables. It illustrates the concept of interventions and how a projection operation simplifies a graph for causal inference. The example is used to discuss different types of identifiability and the limitations of classical methods when functional dependencies are present.

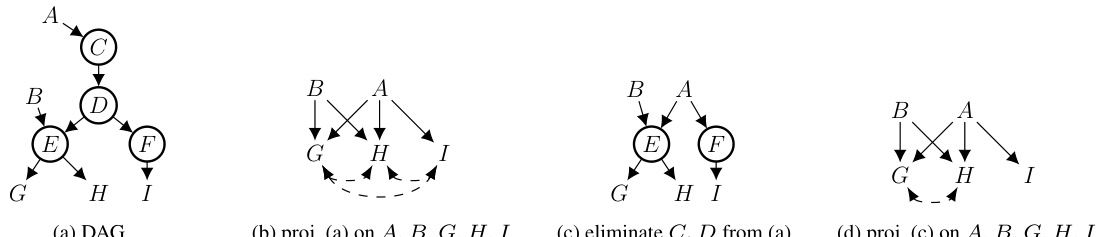
This figure compares classical projection and functional projection on a causal graph. In (a), a DAG is shown with variables A, B, C, D, E, F, G, H, I, where C and D are functional (indicated by circles). (b) shows the result of classical projection onto variables A, B, G, H, I. (c) demonstrates functional elimination of variables C and D. Finally, (d) displays the result of functional projection (eliminating C and D and then projecting onto A, B, G, H, I). The dashed lines highlight the differences between the classical projection and functional projection, showing how functional projection preserves additional independencies.

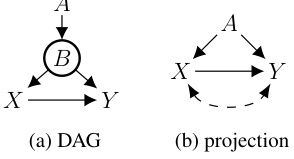
This figure shows a causal graph with observed variables A, X, Y and hidden functional variable B. The graph in (a) depicts the original causal graph, while (b) shows the result of projecting the graph onto the observed variables. The projection operation simplifies the graph by removing the hidden variable and adding a bidirected edge between X and Y, representing the unobserved confounding effect of B. This figure is used to illustrate how knowledge of functional dependencies can affect causal effect identifiability. Specifically, the causal effect of X on Y is unidentifiable in the original graph (a) but may become identifiable if the functional dependency of B on A is considered.

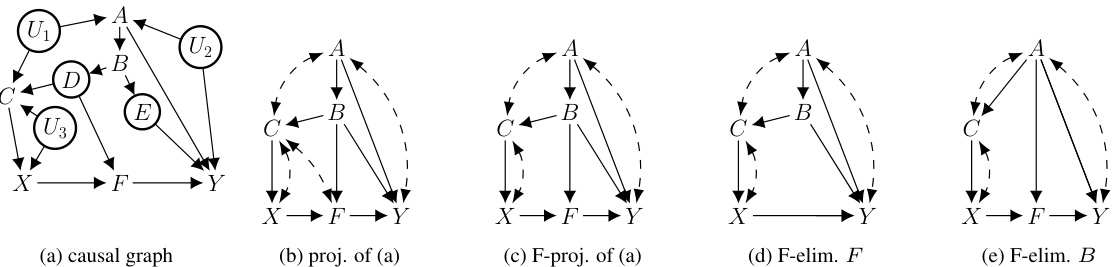
This figure shows a causal graph with observed variables A, B, C, F, X, and Y and hidden functional variables D and E. The figure demonstrates the effects of applying different operations (projection, functional projection, functional elimination) on the causal graph. Each subfigure illustrates the resulting graph after a specific operation. (a) shows the original graph. (b) shows the result of a standard projection. (c) shows the result of a functional projection (which incorporates knowledge about functional dependencies). (d) and (e) show the results of functional elimination (removing functional variables and updating the graph accordingly). These transformations are used in the paper to explore and analyze identifiability of causal effects under functional dependencies.

Full paper

#