↗ OpenReview ↗ NeurIPS Proc. ↗ Chat
TL;DR#
Externalities, indirect effects impacting global welfare from economic interactions, pose a significant challenge in economics. Most models assume perfect knowledge among players, hindering practical implementation. This paper tackles this by extending the Coase Theorem, which suggests property rights and bargaining can optimize social welfare in the presence of externalities, to online settings where players lack complete information.
The researchers employ a two-player multi-armed bandit framework to model economic interactions, where player actions influence others’ rewards. They demonstrate that without property rights, social welfare suffers. To address this, they devise a policy for players to learn bargaining strategies and maximize total welfare. This strategy involves transfers that incentivize actions that benefit overall social welfare, thus extending Coase’s Theorem under conditions of uncertainty and incomplete information. The solution demonstrates a sub-linear social welfare regret, indicating efficiency.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers studying economics, game theory, and online learning. It bridges the gap between theoretical economic models and practical online settings, offering a novel approach to address externalities under uncertainty. This work opens new avenues for developing efficient mechanisms in various applications involving strategic interactions and incomplete information.
Visual Insights#
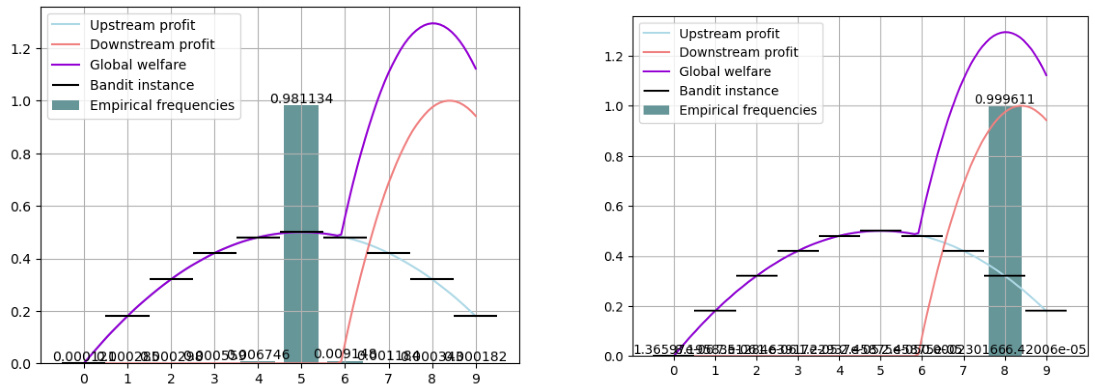
This figure shows the empirical frequencies of actions taken by the upstream player in two scenarios: one without property rights and one with property rights. The left panel depicts the scenario without property rights, demonstrating inefficient outcomes due to the externality, while the right panel shows the efficient outcome achieved when property rights are established and bargaining is possible. The plots illustrate the convergence of the system towards the social welfare optimum when property rights are enforced.
Full paper#