↗ OpenReview ↗ NeurIPS Proc. ↗ Chat
TL;DR#
Many machine learning problems involve optimization over probability measures. However, some crucial problems, like risk minimization for two-layer neural networks or sparse deconvolution, are defined over signed measures, posing challenges for existing methods. Previous attempts to address this involved reducing signed measures to probability measures, but these methods lacked strong guarantees and had slower convergence rates.
This research introduces a novel bilevel approach to extend the framework of mean-field Langevin dynamics (MFLD) to handle signed measures. The authors demonstrate that this approach leads to significantly improved convergence guarantees and faster convergence rates. Their findings also include an analysis of a single neuron model under the bilevel approach, showing local exponential convergence with polynomial dependence on the dimension and noise level, a result that contrasts with prior analyses that indicated exponential dependence.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working on optimization problems over signed measures, which are common in machine learning and other fields. It provides stronger convergence guarantees and faster rates for existing methods, opening up new avenues for research into efficient algorithms for these problems. The bilevel approach offers a superior alternative to previous methods, enhancing the reliability and efficiency of these algorithms. The analysis of a single-neuron learning model contributes to a deeper understanding of local convergence rates, offering valuable insights into the behavior of these models.
Visual Insights#
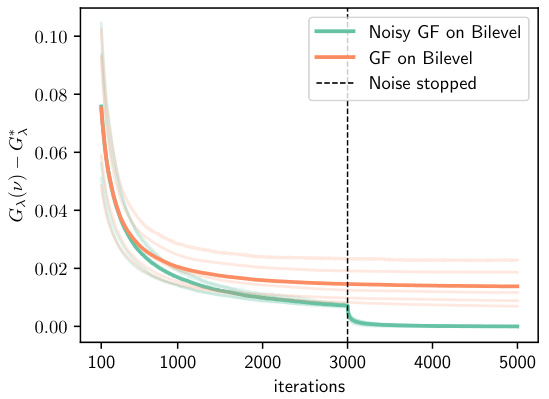
This figure compares the performance of different optimization methods for training a two-layer neural network (2NN) with a ReLU activation function. It shows the training loss (Gx(ν)) over iterations for different approaches, including using the bilevel and lifting formulations. The results highlight the superior performance of the bilevel approach, specifically when using Mean-Field Langevin Dynamics (MFLD). The figure also illustrates the impact of noise on the training process and the effect of different choices of metric in the optimization process.
Full paper#