↗ OpenReview ↗ NeurIPS Proc. ↗ Hugging Face ↗ Chat
TL;DR#
Modern generative models exhibit impressive capabilities, but fundamental questions remain about how and why they learn specific concepts. Existing methods often struggle to analyze learning at the concept level, leading to a lack of understanding about the emergence of hidden capabilities—abilities a model possesses but does not readily demonstrate. This paper proposes that generative models possess latent capabilities that emerge suddenly and consistently during training, even though these capabilities might not be easily elicited using naive input prompting.
To address this, the paper introduces a novel framework called “concept space”, where each axis represents an independent concept. By analyzing learning dynamics within this concept space and using a concept signal metric, the researchers show that the order and speed of concept learning are controlled by the properties of the data. Furthermore, they identify moments of sudden turns in learning trajectories which correspond to the emergence of hidden capabilities. The study, while primarily focused on synthetic data, lays a groundwork for understanding and potentially improving the training and interpretability of generative models, suggesting a shift from focusing solely on performance to considering the model’s underlying competence.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in generative models, particularly those working on disentanglement and interpretability. It introduces a novel framework for analyzing learning dynamics, offering valuable insights into the emergence of hidden capabilities and providing a strong theoretical foundation for future research. The concept space framework is broadly applicable and its findings on hidden capabilities may extend beyond the toy models explored.
Visual Insights#
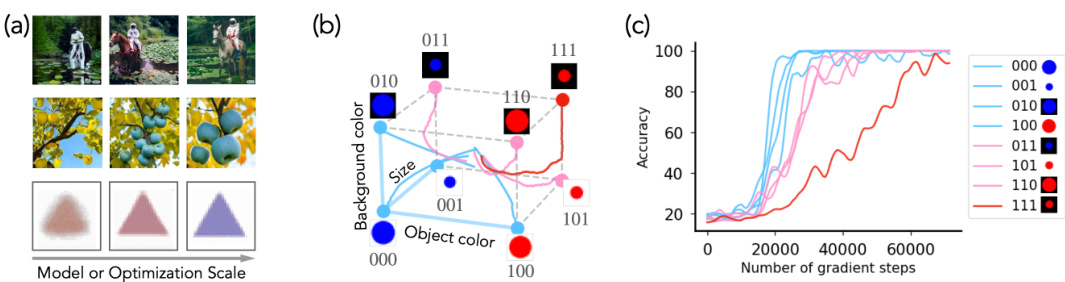
This figure demonstrates the concept of concept learning geometry and how it relates to the emergence of capabilities in generative models. It shows that the order in which a model learns concepts (e.g., astronaut, horse, riding; apple, blue, square) is reflected in its learning trajectory in a multi-dimensional concept space. Each axis in this concept space represents an independent concept (e.g., shape, color, size), and the model’s progress through the space reveals the order and speed of its learning. The figure illustrates how the ‘concept signal,’ or the degree to which the data-generating process is sensitive to changes in a specific concept, influences learning speed and order. Sudden changes in learning direction in concept space correspond to the emergence of ‘hidden’ capabilities—the model is able to manipulate a concept internally, but this capability is not yet demonstrable via naive input prompting.
In-depth insights#
Hidden Capabilities#
The concept of “hidden capabilities” in generative models refers to the latent potential within these models that is not readily apparent during standard operation. These capabilities only emerge under specific conditions or prompts, showcasing a discrepancy between a model’s actual competence and its observable performance. The paper explores the dynamics of learning in generative models, highlighting how these hidden capabilities might develop through various stages. This phenomenon of emergence involves a sudden shift in learning trajectories that is clearly detectable within a conceptual framework called “concept space.” Concept signal, a measure of data sensitivity to specific concepts, dictates how readily a model learns to manipulate them. Stronger concept signals lead to faster learning and earlier emergence of abilities, while weaker ones delay the unfolding of potential. Importantly, the study suggests that hidden capabilities exist before they can be effectively elicited through simple inputs, emphasizing the importance of exploring latent interventions to fully assess model competence. This highlights a significant limitation in evaluating models solely based on naive prompting and calls for more sophisticated methods to truly unlock and understand the full potential of generative AI.
Concept Space#
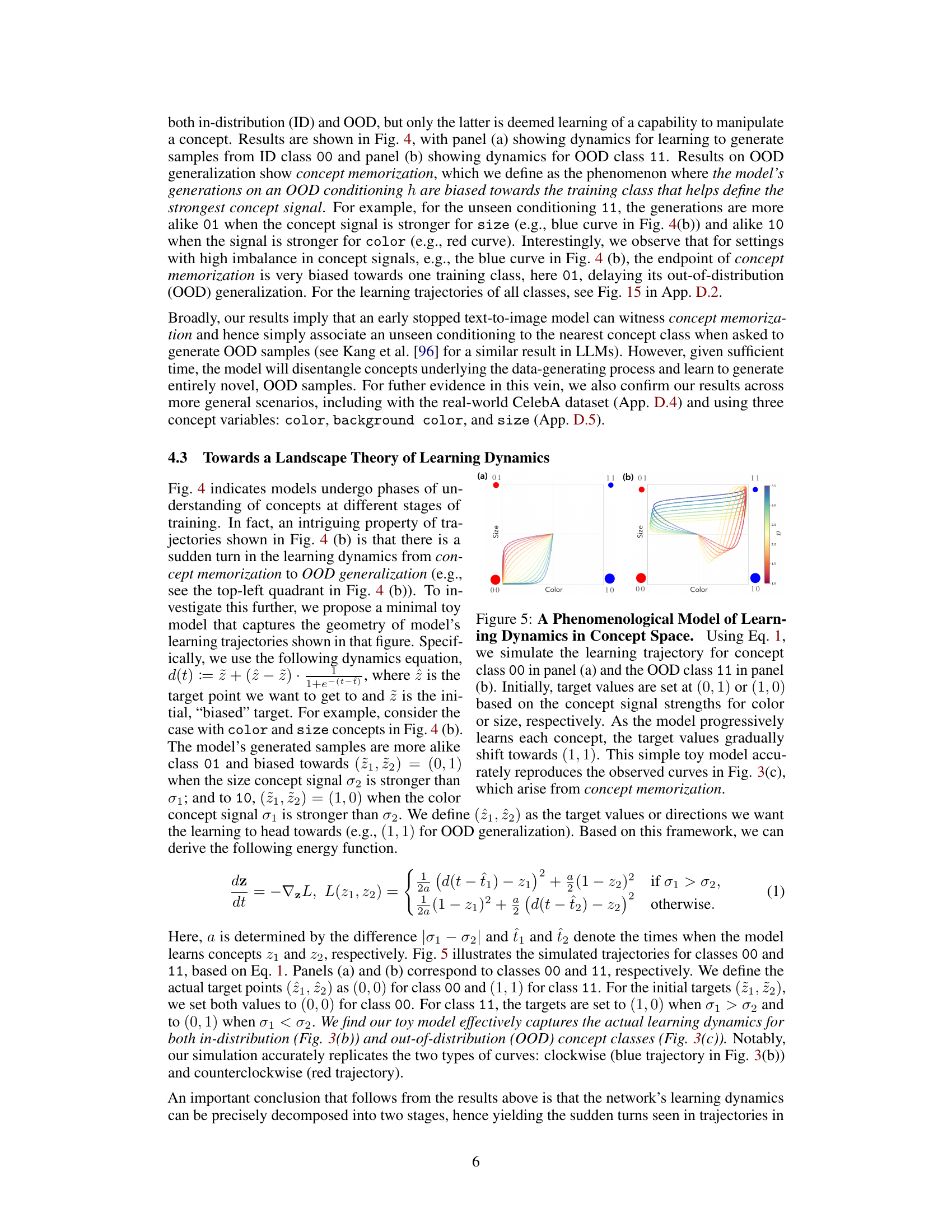
The concept of ‘Concept Space’, as described in the research paper, offers a novel framework for analyzing the learning dynamics of generative models. It posits that each axis in this multi-dimensional space represents an independent concept underlying the data generating process. By tracking a model’s trajectory through this space, researchers gain insights into the order in which concepts are learned, and how the speed of learning is modulated by various factors. A crucial element is ‘concept signal’, which quantifies the sensitivity of the data-generating process to changes in the value of a given concept. Stronger signals generally lead to faster learning. Moreover, this framework provides a means to identify ‘hidden capabilities’, where latent interventions reveal a model’s ability to manipulate a concept even before such capabilities become readily apparent through standard input prompting. The concept space thus offers a detailed perspective on a generative model’s learning process, including the emergence of latent skills that might otherwise remain undetected. Sudden turns in the model’s trajectory within the concept space signal the emergence of these hidden capabilities. This suggests a phase transition in the model’s learning, moving from concept memorization to OOD generalization.
Signal & Learning#
The relationship between signal quality and learning speed is a core theme in many machine learning models. A strong signal, clearly indicating the relevant features, enables faster learning. Conversely, weak or noisy signals impede learning, often leading to slower convergence or poor generalization. Concept signal, as defined in this research, directly quantifies how much the data generating process changes with alterations to a specific underlying concept. This framework is powerful because it helps explain why models learn some concepts faster than others and how data properties shape the learning dynamics. Hidden capabilities, often unexpected emergent behaviors, are closely linked to sudden transitions in the concept space, highlighting the importance of considering not only immediate performance but also latent capabilities that may emerge later during training.
Concept Transitions#
The concept of ‘Concept Transitions’ in a research paper likely refers to shifts or changes in the way a model understands and manipulates underlying concepts during the learning process. A thoughtful analysis would explore how these transitions manifest, their relationship to the emergence of new capabilities, and the factors influencing their timing and nature. For instance, it could investigate whether transitions occur gradually or abruptly, whether they are associated with changes in the model’s internal representations, and what role data characteristics play in shaping the process. Identifying specific triggers for these transitions, such as reaching certain training milestones or encountering particular data patterns, would be crucial. Furthermore, a key aspect of this analysis would be to differentiate between expected, smooth transitions and unexpected, potentially discontinuous ones. The presence of sudden shifts might signify a phase transition in the model’s learning dynamics, potentially linked to the discovery of hidden capabilities that were previously inaccessible. Ultimately, understanding concept transitions is vital for building more robust, interpretable, and reliable models.
Underspecification#
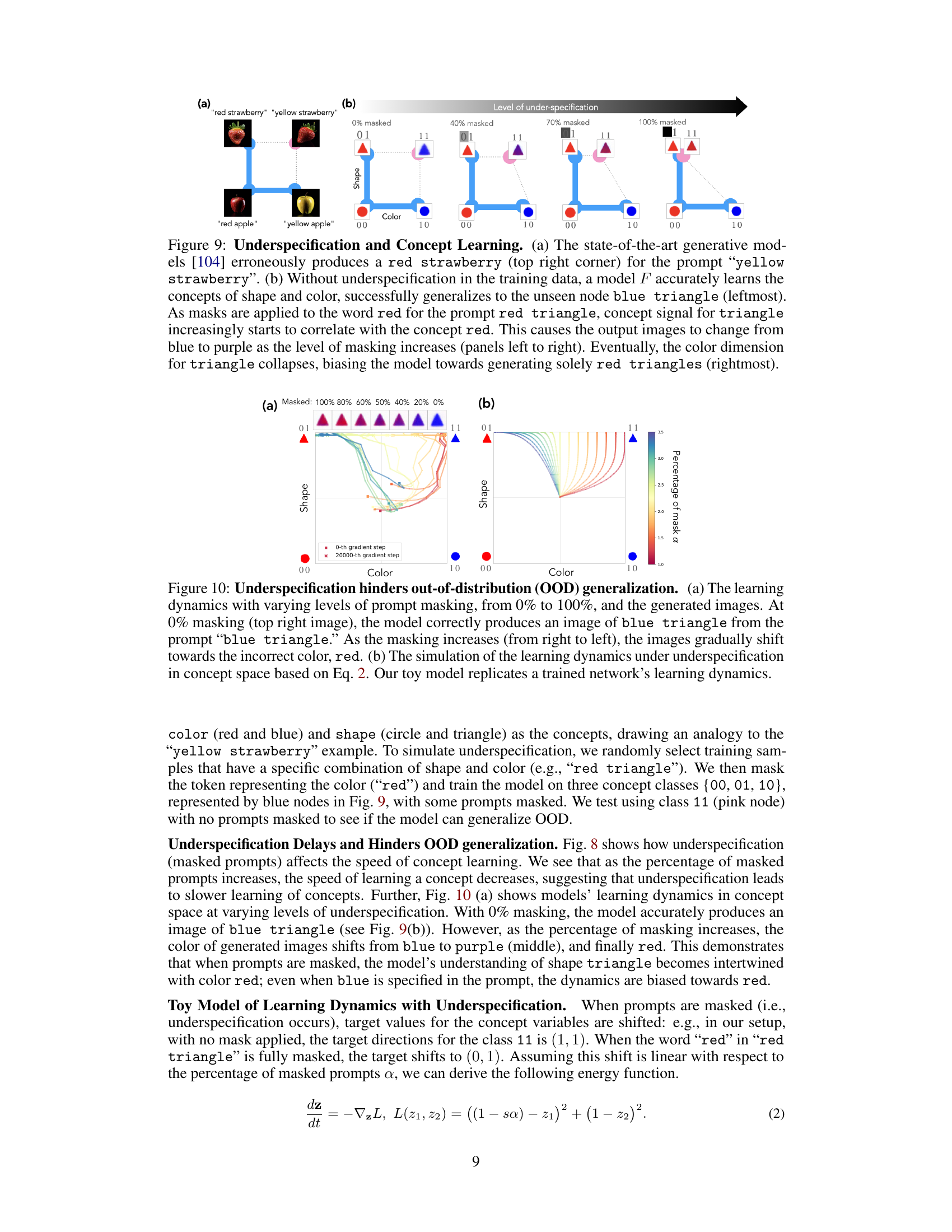
The concept of ‘underspecification’ in the context of this research paper centers on the imprecision inherent in the instructions or conditioning information provided to generative models. Unlike precisely defined synthetic data, real-world instructions are often vague, leading to correlations between concepts that are not explicitly stated. This ambiguity significantly impacts the model’s ability to disentangle concepts, hindering its capacity to learn each independently. The study shows that underspecification directly influences the speed of learning, potentially delaying or preventing the model from acquiring specific capabilities. In essence, when concepts are correlated, the model fails to fully separate and learn these concepts individually. This limitation significantly impacts the emergence of hidden capabilities, where the model may implicitly grasp a concept but cannot demonstrate it due to the underspecified nature of prompting. The research emphasizes the importance of analyzing how the model handles underspecification to better understand and potentially improve the learning dynamics and generalization abilities of generative models.
More visual insights#
More on figures
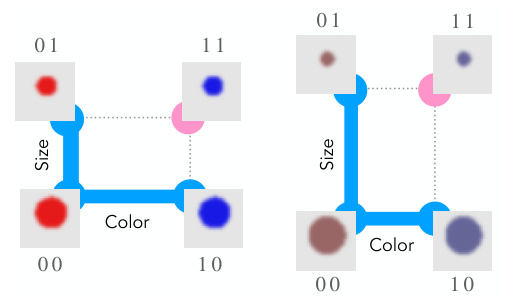
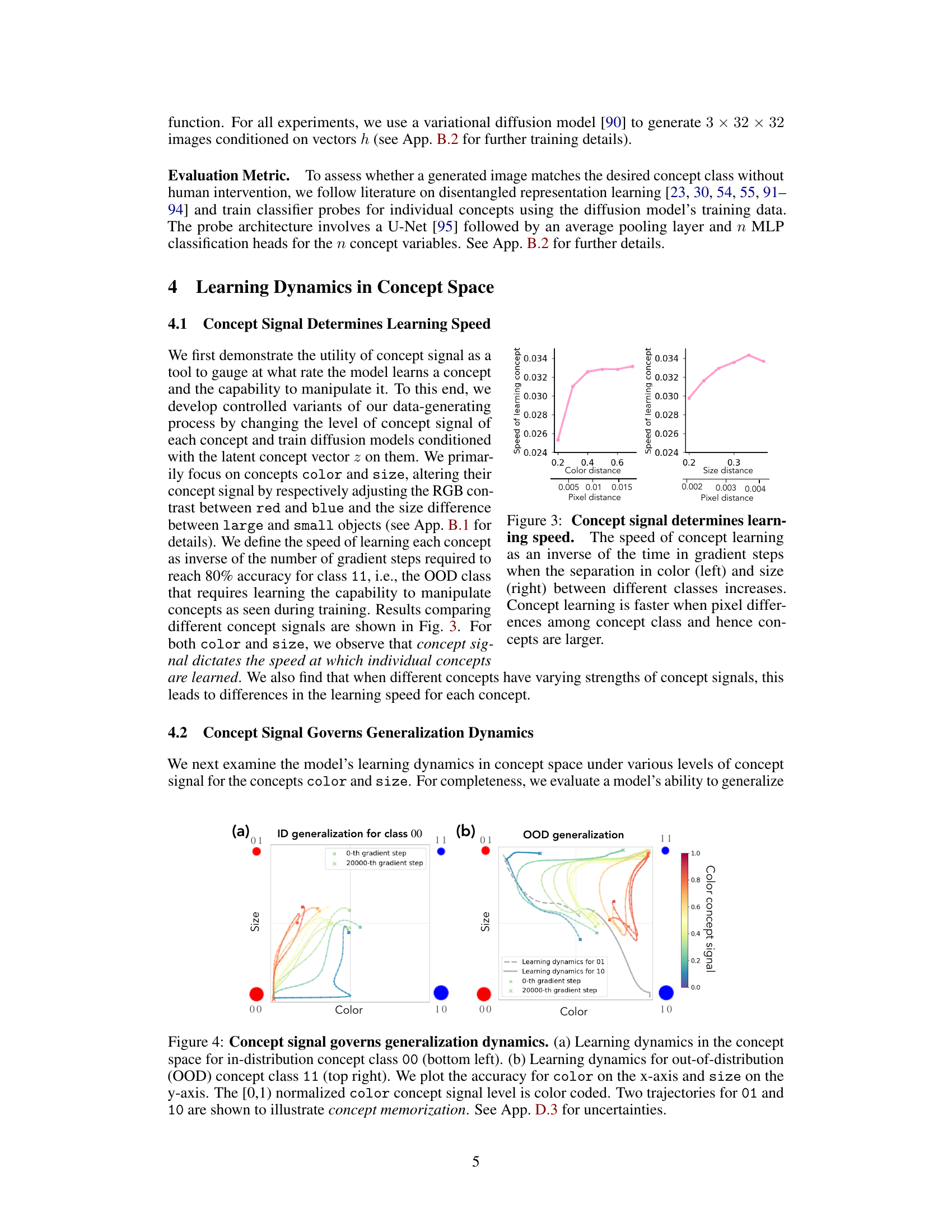
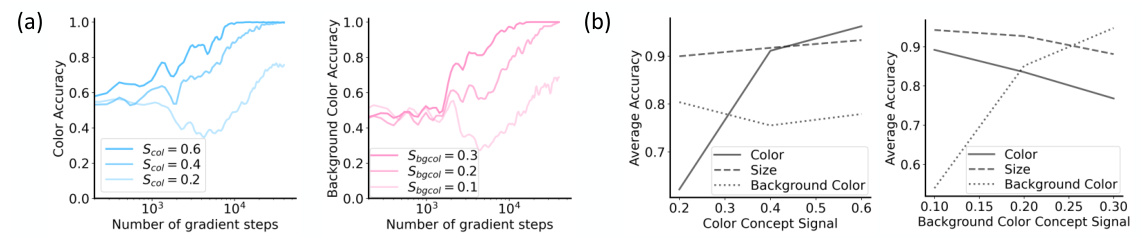
This figure shows how different distributions of concept values (color and size) affect the concept signal strength. The left panel illustrates a scenario where the difference in color between classes is greater than the size difference, resulting in a stronger color concept signal. The right panel demonstrates the opposite: a larger size difference yields a stronger size concept signal. This difference in concept signal strength influences how quickly the model learns each concept.
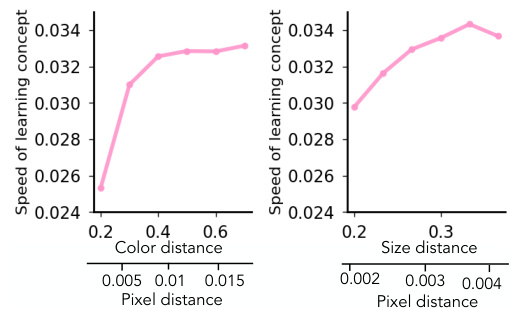
This figure shows the relationship between concept signal and learning speed in a generative model. The left panel illustrates that as the color difference (distance) between classes increases, the speed at which the concept of color is learned increases. Similarly, the right panel shows this same trend for the size concept. The faster learning speed is correlated with a larger pixel difference between the classes.
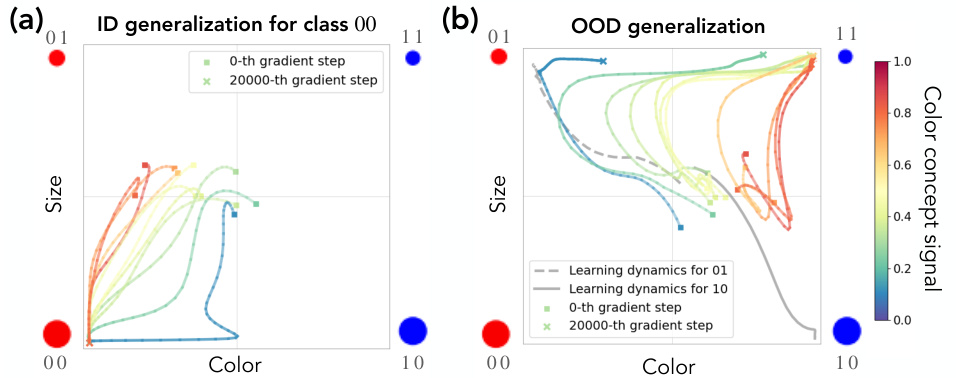
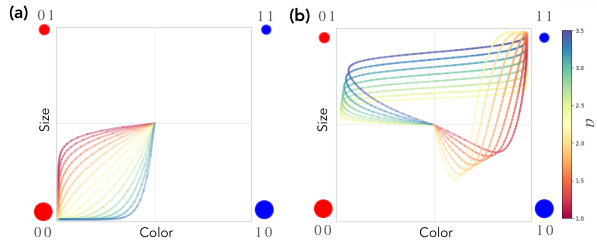
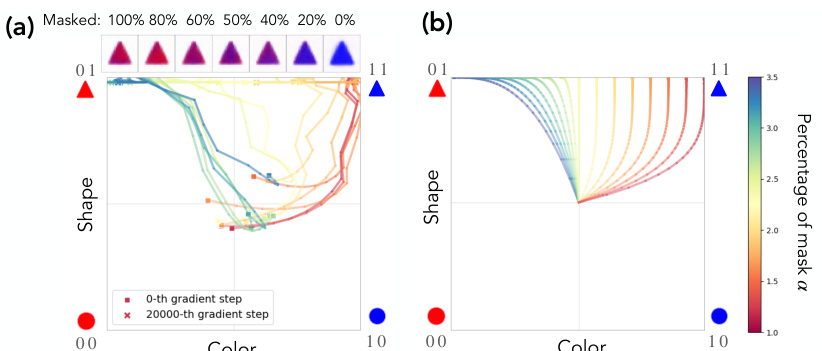
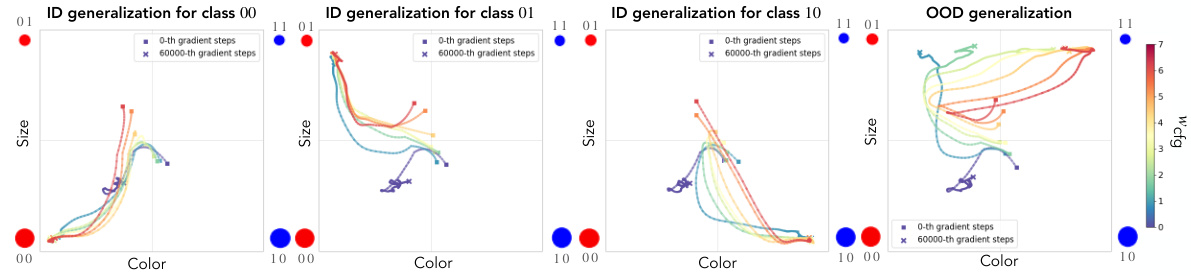
This figure visualizes the learning dynamics of a model in concept space, a coordinate system representing underlying concepts. Panel (a) shows the in-distribution learning trajectory for concept class 00, while panel (b) illustrates the out-of-distribution (OOD) learning for concept class 11. The x-axis represents color accuracy, and the y-axis represents size accuracy. The color intensity corresponds to the concept signal strength, showing how sensitive the data generation process is to changes in the concept’s value. The trajectories reveal how the model learns and generalizes, showing memorization effects (biased towards previously seen data) and a sudden transition to OOD generalization.
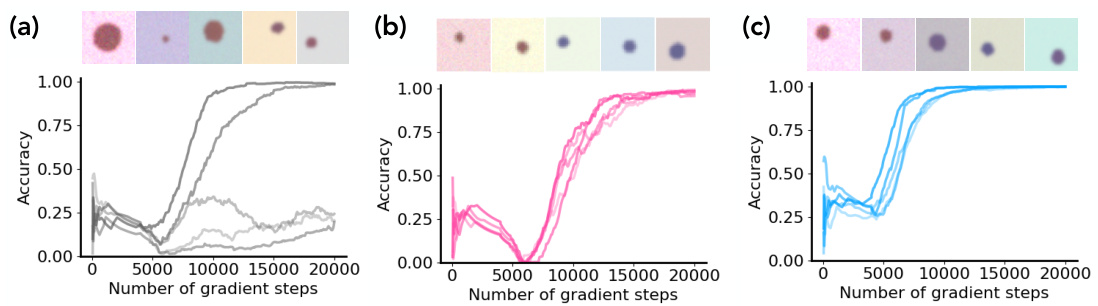
This figure shows how underspecification (masking words in prompts) affects a model’s ability to generalize to out-of-distribution (OOD) examples. Panel (a) displays the generated images for different levels of masking, demonstrating a shift from correct blue triangles (no masking) to incorrect red triangles (100% masking). Panel (b) presents a simplified model that successfully replicates the learning dynamics observed in (a), providing a theoretical explanation for the effect of underspecification.
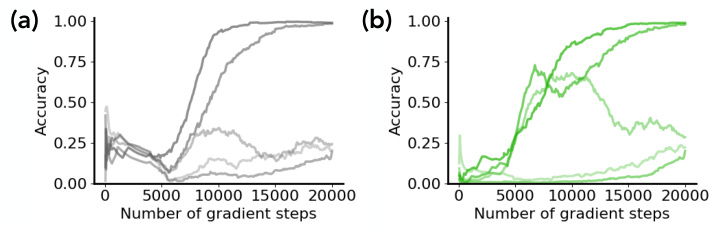
This figure shows the accuracy of generating out-of-distribution (OOD) samples over the number of gradient steps using three different prompting methods: naive prompting, linear latent intervention, and overprompting. Each method’s accuracy is plotted for five separate runs, demonstrating that while naive prompting may fail to elicit a hidden capability, linear latent intervention and overprompting reliably do so earlier in the training process. This suggests that the model acquires the capability to manipulate the relevant concepts before this capability is readily apparent using standard input prompting.
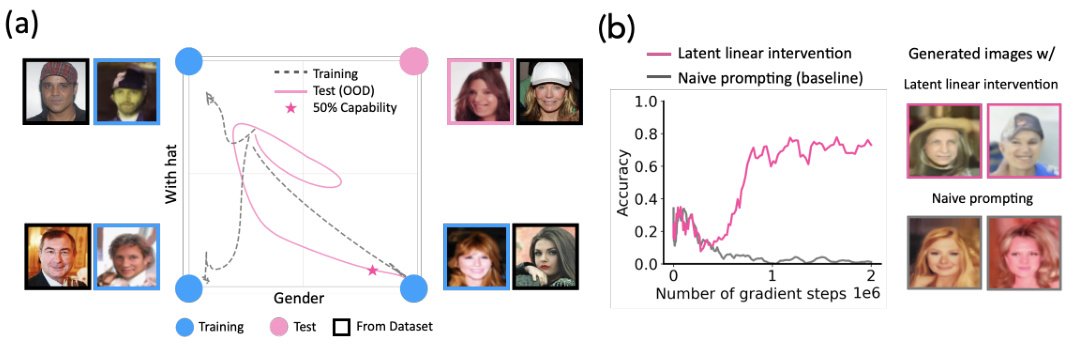
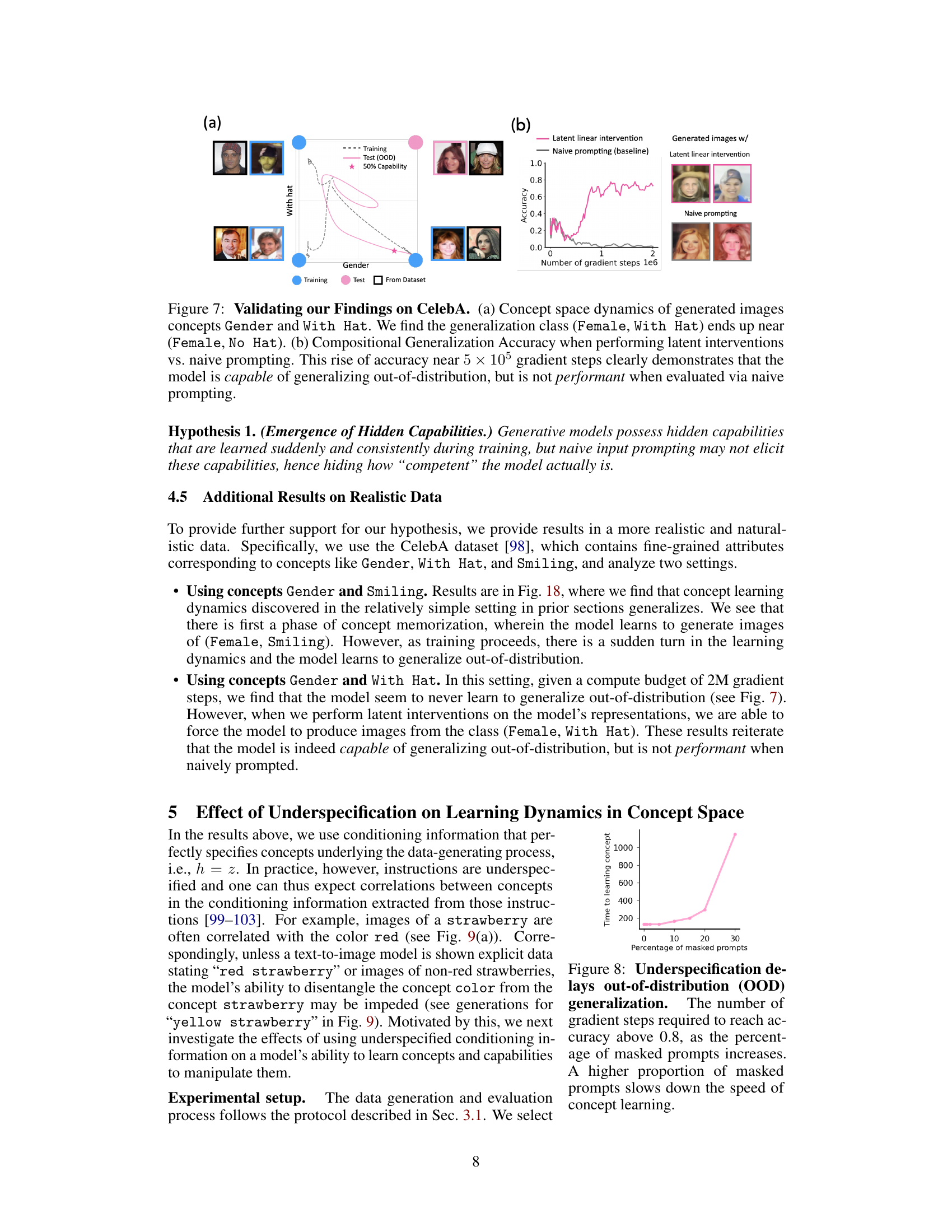
This figure validates the findings of the paper using the CelebA dataset. Panel (a) shows the concept space dynamics for the concepts ‘Gender’ and ‘With Hat.’ It demonstrates that the model initially memorizes concepts from the training data, exhibiting a bias toward certain concept combinations. However, as the training progresses, the model transitions to out-of-distribution generalization, with the generated images moving closer to the target class (Female, With Hat). Panel (b) quantitatively assesses the model’s compositional generalization ability by comparing the accuracy achieved using latent interventions versus naive prompting. The results reveal a significant increase in accuracy near 500,000 gradient steps when latent interventions are used, showing the model’s hidden capability to perform well on unseen data, which is not apparent under standard prompting.
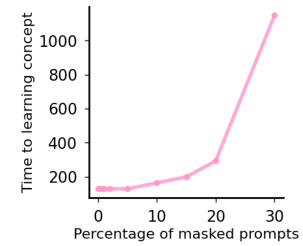
This figure shows how the speed of learning a concept decreases as the percentage of masked prompts (representing underspecification) increases. The y-axis shows the number of gradient steps required to reach 80% accuracy. Underspecification hinders the model’s ability to quickly disentangle and learn concepts. The slower learning is due to correlations introduced between concepts by the masked prompts, making it more difficult for the model to learn the separate concepts independently.
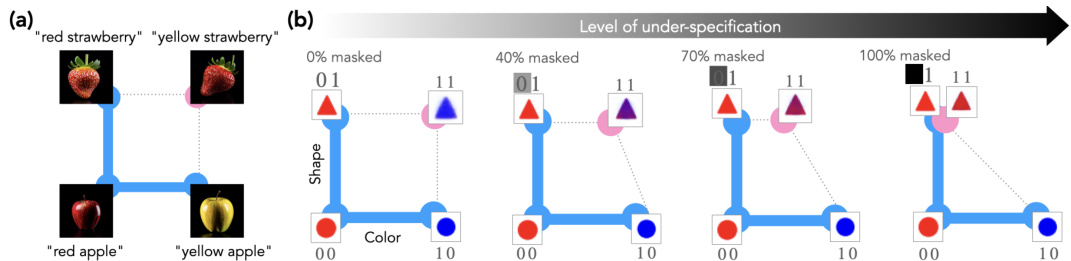
This figure demonstrates the effect of underspecification on concept learning in a generative model. Panel (a) shows an example of a state-of-the-art model failing to generate a yellow strawberry when prompted with ‘yellow strawberry’, instead producing a red one. This highlights the issue of underspecification in real-world prompts. Panel (b) uses a simplified model to illustrate how increasing levels of masking (removing the word ‘red’ from ‘red triangle’) causes the model’s learning to become biased towards red, even when prompted with ‘blue triangle’. The results show that underspecification hinders the ability of the model to disentangle concepts and generalize correctly to unseen data.
This figure shows how underspecification in training data affects the model’s ability to generalize to out-of-distribution (OOD) examples. Panel (a) presents empirical results illustrating how increasing levels of prompt masking (removing the color word from the prompt) causes the model to generate images with increasingly incorrect colors, even though the correct color is specified in the prompt’s remaining words. Panel (b) displays results from a simplified mathematical model that mirrors the trends observed in the empirical results, providing further support for the hypothesis that underspecification hinders the learning process and generalization performance.
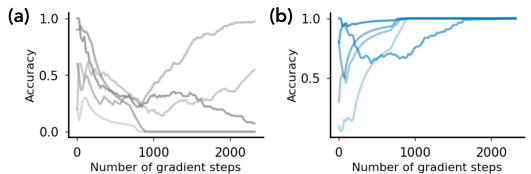
This figure shows the accuracy of generating out-of-distribution (OOD) samples using three different prompting methods: naive prompting, linear latent intervention, and overprompting. The results demonstrate that while naive prompting may not elicit the model’s hidden capabilities, latent interventions and overprompting can successfully generate OOD samples. This supports the hypothesis that generative models possess hidden capabilities that are learned suddenly and consistently during training but may not be immediately apparent due to limitations of naive input prompting. This figure belongs to the ‘Sudden Transitions in Concept Learning Dynamics’ section of the paper.
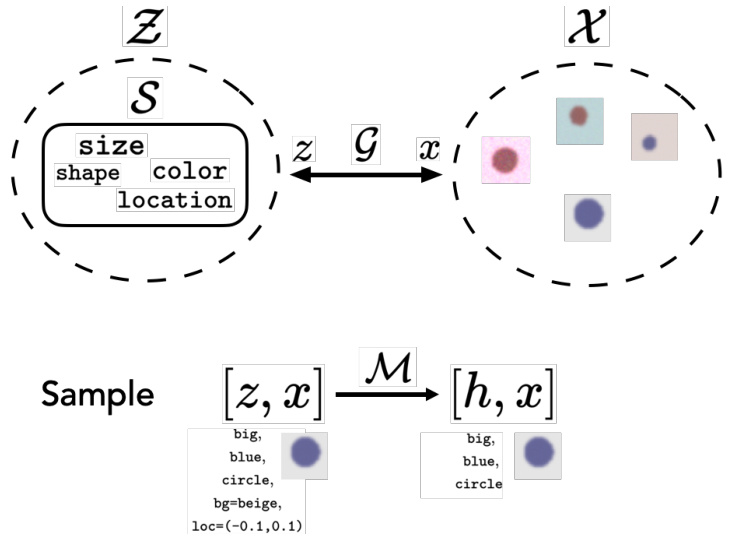
This figure illustrates the concept space framework. It shows a data-generating process (G) that maps a vector z from a concept space (S) to an observation x (an image). The concept space has dimensions representing independent concepts like size, shape, color, and location. A mixing function (M) then maps z and x to h and x, representing how some concepts might be underspecified in the conditioning information used to generate images.
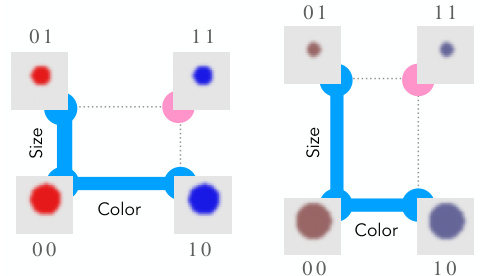
This figure shows two examples of concept spaces with different concept signals. In the left panel, the color difference between classes is greater than the size difference, resulting in a stronger concept signal for color. Conversely, in the right panel, the size difference between classes is greater than the color difference, leading to a stronger concept signal for size. This illustrates how variations in the data-generating process, specifically the distances between concept classes, impact the strength of the concept signal for each concept.
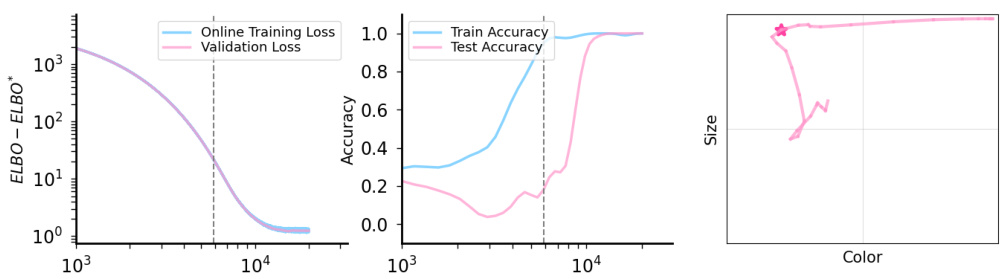
This figure shows a comparison of three different metrics (loss, training accuracy, and test accuracy) plotted against the number of gradient steps during training. The leftmost panel displays the training loss in log scale which reveals the general training progress. The middle panel depicts the training and test accuracies showing the generalization ability of the model. The rightmost panel shows the model’s learning trajectory in the concept space. A sudden shift in the trajectory indicates the emergence of a hidden capability, a point where the model suddenly starts to generate correct outputs despite the lack of explicit signal from naive prompting. The pink star in the rightmost panel highlights the moment when the capability emerges.
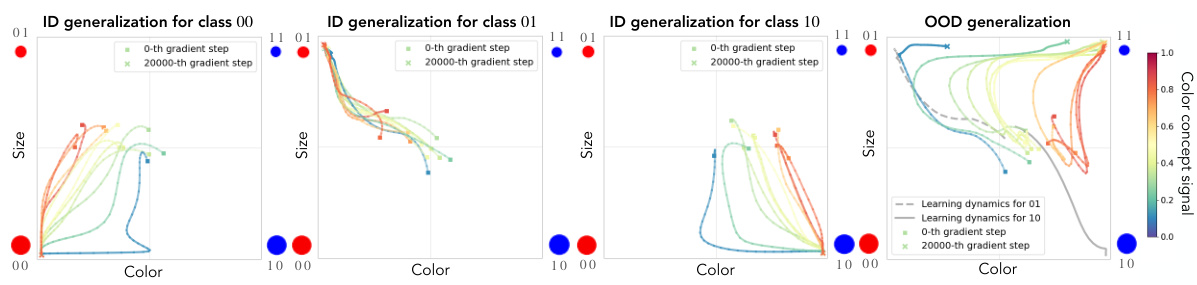
This figure shows the learning dynamics of a generative model in a concept space with ‘color’ and ‘size’ as axes. Panel (a) displays the model’s learning trajectory for an in-distribution concept class (00), while panel (b) shows the trajectory for an out-of-distribution (OOD) class (11). The color of the trajectories represents the level of color concept signal, illustrating how the signal influences the learning process. The figure demonstrates that concept memorization occurs before OOD generalization, showing a shift in learning dynamics. The plot highlights the role of concept signal in shaping the model’s generalization capabilities and learning trajectory.
This figure shows the learning dynamics of a generative model in a 2D concept space (color and size). Panel (a) shows the learning trajectory for an in-distribution class (00), while panel (b) shows the learning trajectory for an out-of-distribution class (11). The color of the trajectory represents the color concept signal. The figure illustrates how concept signal influences the learning dynamics and how the model initially memorizes concepts before generalizing out-of-distribution. The uncertainty of the model is represented by color coding.
This figure shows the accuracy of generating out-of-distribution (OOD) samples using three different prompting methods: naive prompting, linear latent intervention, and overprompting. It demonstrates that while naive prompting may fail to elicit the model’s hidden capabilities, latent interventions and overprompting can successfully generate the desired outputs much earlier in the training process. This suggests a two-stage learning process: first, the model acquires the latent capability, and second, it learns to map inputs to outputs.

This figure shows the results of experiments conducted on the CelebA dataset to validate the findings of the paper on a more realistic dataset. Panel (a) displays the concept space dynamics for generating images based on the ‘Gender’ and ‘With Hat’ concepts. It reveals that even though the model learns to generate images of (Female, With Hat), the model’s performance using naive prompting is suboptimal; the generated images cluster closer to (Female, No Hat). Panel (b) demonstrates improved generalization when using latent interventions rather than naive prompting, indicating that the model possesses hidden capabilities that are not readily apparent under naive prompting.
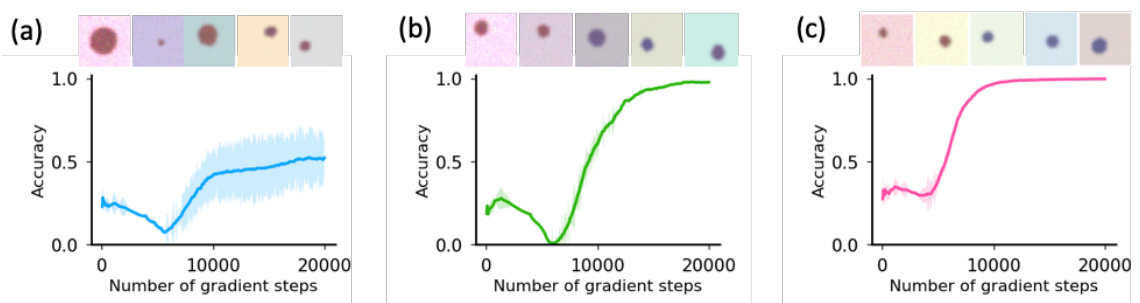
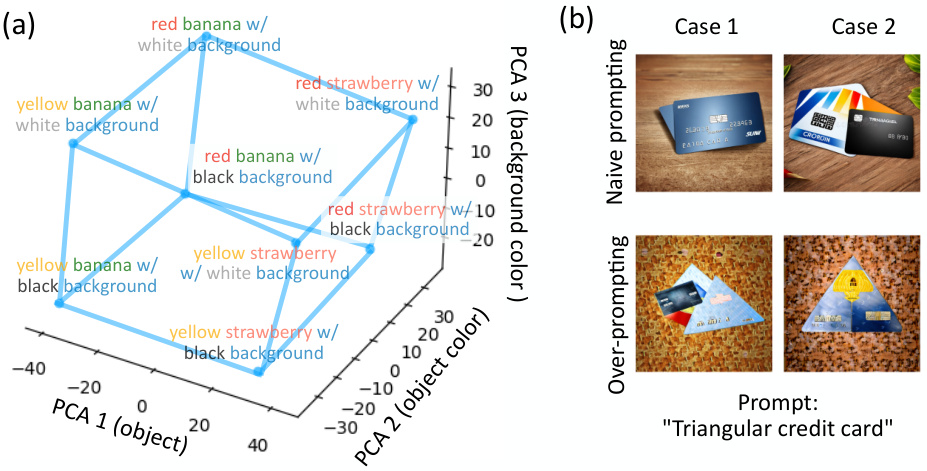
This figure shows two examples of concept learning dynamics in a 3D concept space, illustrating both successful and unsuccessful out-of-distribution (OOD) generalization. In (a), the strong concept signal for color leads to successful OOD generalization, while in (b), the weaker concept signal for background color results in failure to generalize. The trajectories in the 3D concept space visualize the model’s learning process, revealing how concept learning order and OOD generalization are affected by concept signal strength.
This figure shows the effect of underspecification (masking words in prompts) on a model’s ability to generalize to out-of-distribution data. Panel (a) demonstrates that as more words are masked from the prompts (e.g., masking ‘blue’ in ‘blue triangle’), the generated images increasingly shift towards an incorrect color (red). Panel (b) shows a simplified model which successfully recreates the same pattern of learning dynamics observed in the experimental results. This supports the idea that underspecification affects the learning process and generalization.
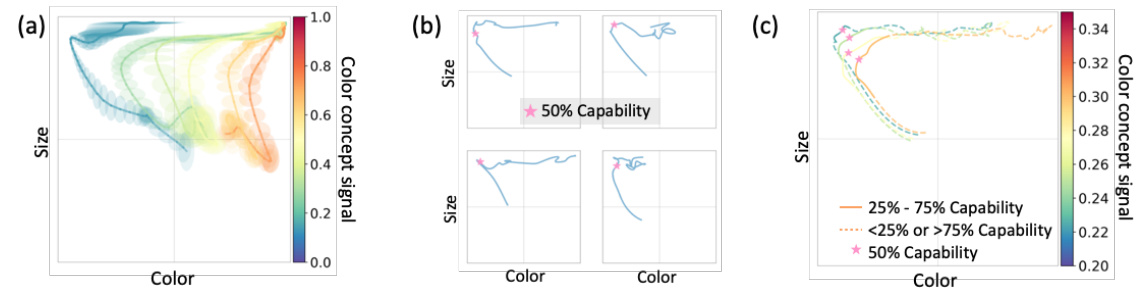
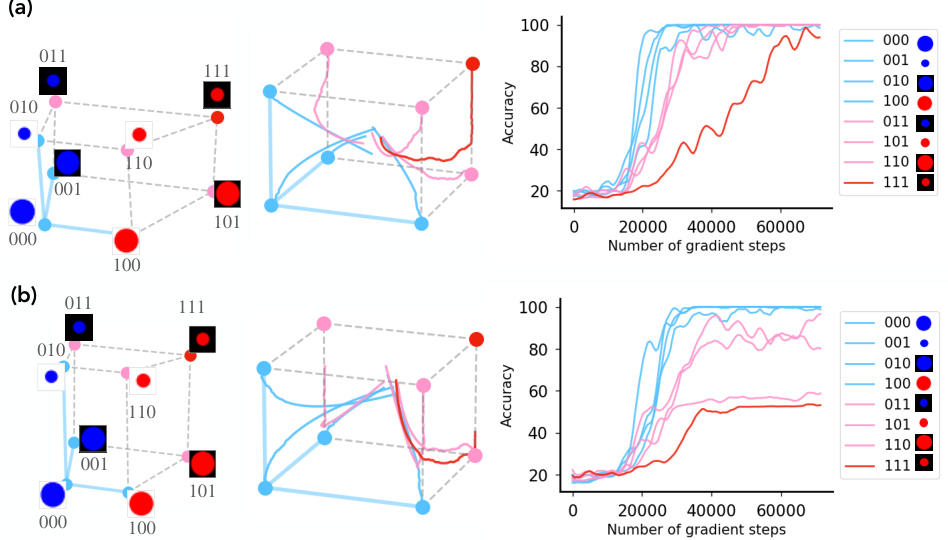
This figure shows the concept learning dynamics for all four classes (00, 01, 10, 11) in the concept space. The color of the trajectories represents the normalized concept signal, indicating the relative strength of the concept signal for color. The two gray trajectories are from the training set and illustrate how concept memorization occurs before generalization.
This figure shows the results of an experiment where the embedding module of a diffusion model was patched with an embedding module from an intermediate checkpoint during training. The goal was to determine if the model had already learned the ability to generate out-of-distribution (OOD) samples before naive prompting methods could elicit this ability. Panel (a) shows the baseline accuracy for OOD generalization using naive prompting. Panel (b) shows the improvement in accuracy when using the patched embedding module, demonstrating that the model had already acquired the capability earlier than revealed by naive prompting.
This figure visualizes the learning dynamics of a generative model in a concept space, where each axis represents a concept (e.g., color and size). Panel (a) shows the learning trajectory for an in-distribution class, while panel (b) shows the trajectory for an out-of-distribution class. The color coding represents the concept signal strength. The trajectories illustrate that the model undergoes a phase of memorization followed by a sudden transition to OOD generalization.
Full paper#