Continual learning with the neural tangent ensemble

↗ OpenReview ↗ NeurIPS Proc. ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial because it offers a novel perspective on neural networks, viewing them not as monolithic entities but as ensembles of individual classifiers. This framework provides new insights into the dynamics of neural network optimization and offers a principled way to address catastrophic forgetting in continual learning. It also opens avenues for developing more effective optimization algorithms and interpreting neural networks through a Bayesian lens. This work could significantly impact various fields using neural networks for continual learning problems.

Visual Insights

#

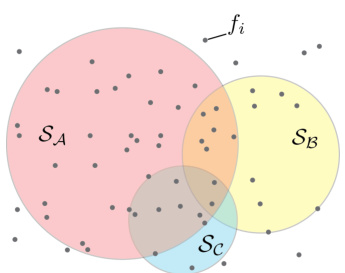
This figure illustrates the concept of continual learning using Bayesian ensembles. It shows three overlapping circles representing sets of functions (experts) that perform well on tasks A, B, and C respectively. The intersection of the circles represents functions good for multiple tasks. Continual learning is presented as a process of pruning (removing) functions that don’t perform well on a task, while retaining those shared across tasks, resulting in an ensemble that does not forget previously learned information.

This algorithm describes the process of updating the weights of a neural network using a Bayesian approach. The algorithm interprets the network as an ensemble of classifiers (experts), where each parameter in the network corresponds to an expert. It updates the weights based on the posterior probability of each expert given the data, which approximates stochastic gradient descent. The algorithm includes steps for calculating the likelihood of each expert given the current example, updating the expert’s weight multiplicatively, renormalizing the weights, and optionally clipping the weight changes to prevent excessively large adjustments. The primary goal is to mitigate catastrophic forgetting in continual learning.

In-depth insights

#

Lazy Regime Learning

#

Lazy regime learning, a fascinating concept in the context of neural networks, describes the behavior where network parameters change minimally during training. This contrasts with the rich regime, where substantial changes are observed. In the lazy regime, a network’s predictions primarily shift due to the initial weights rather than substantial adjustments during learning. This property leads to several intriguing implications, including mitigation of catastrophic forgetting in continual learning. The Neural Tangent Kernel (NTK) framework provides a mathematical basis for understanding this phenomenon. Fixed classifiers become a prominent feature, as the network acts as a weighted ensemble of experts whose outputs remain relatively stable. However, this simplicity holds true mainly in the infinite-width limit and is an approximation for finite-width networks. The practical benefits involve simplifying continual learning, enabling the estimation of full Bayesian posteriors, and offering a novel interpretation of gradient descent as posterior updates.

NTE Posterior Update

#

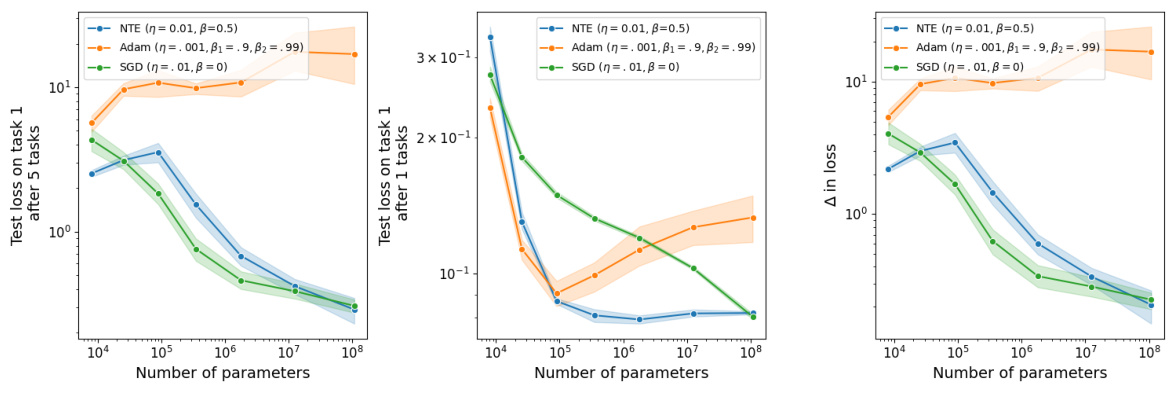
The Neural Tangent Ensemble (NTE) posterior update offers a novel perspective on neural network learning, framing it as Bayesian inference rather than mere optimization. This Bayesian approach elegantly addresses the catastrophic forgetting problem inherent in continual learning by representing a network as a weighted ensemble of fixed classifiers (neural tangent experts). The update rule, surprisingly, closely approximates stochastic gradient descent (SGD), providing a deeper understanding of SGD’s dynamics. While initially derived for the lazy regime where experts remain fixed, the framework extends to rich regimes by allowing experts to adapt over time, essentially becoming a particle filter. This adaptive mechanism enables continual learning without the memory overhead of storing past data, making it a promising strategy for lifelong learning. The elegance of NTE lies in its unification of Bayesian principles and gradient-based optimization, offering a novel lens through which to analyze and improve neural network learning.

Momentum’s Impact

#

The study reveals a detrimental impact of momentum on continual learning. Momentum, while beneficial for single-task learning by accelerating convergence, disrupts the Bayesian posterior update mechanism crucial for continual learning. The authors demonstrate that momentum hinders the ability of networks to retain previous knowledge when learning subsequent tasks, leading to catastrophic forgetting. This is because momentum incorporates past gradients into current updates, thus violating the order-invariance property essential for effective continual learning in Bayesian ensembles. The results highlight that momentum’s additive update rule conflicts with the multiplicative nature of Bayesian posterior updates, which are order-invariant and crucial for maintaining information about previously learned tasks. Therefore, to mitigate catastrophic forgetting, the authors recommend alternative optimization strategies that closely approximate Bayesian updates, emphasizing the importance of order-invariance for lifelong learning. The findings underscore that optimal continual learning algorithms should avoid momentum-based optimizers and focus on techniques that align with the inherent principles of Bayesian inference.

Width’s Effects

#

The paper investigates the effects of network width on continual learning, particularly focusing on how wider networks mitigate catastrophic forgetting. Wider networks, it is argued, remain closer to the lazy regime, where the network’s Jacobian (the matrix of gradients) changes minimally during training. This allows the Neural Tangent Ensemble (NTE) interpretation of the network, where each weight represents a classifier, to hold more accurately. In this regime, the NTE posterior update rule (approximately equivalent to stochastic gradient descent), allows for continual learning without significant forgetting. However, the study also shows that this relationship between width and forgetting reduction is highly dependent on the chosen optimization algorithm. While SGD exhibits this behavior, the use of algorithms like Adam doesn’t yield the same benefit, highlighting the critical role of the optimization strategy in harnessing the effects of network width for effective continual learning. Furthermore, the research suggests that networks in the rich regime exhibit adaptive experts, meaning that the initialization point for the Taylor expansion shifts over time, allowing the network to continually refine its ensemble of classifiers and adapt to new tasks more effectively.

Future Directions

#

Future research could explore several promising avenues. Extending the Neural Tangent Ensemble (NTE) framework beyond the lazy regime is crucial. This involves developing methods to handle the dynamic nature of experts in richer regimes, potentially through adaptive seed point selection or incorporating higher-order Taylor expansion terms. Investigating the interplay between network architecture and the NTE is another key area. Exploring how different network depths, widths, and activation functions affect the behavior of NTE experts could lead to significant insights into continual learning. Finally, a deeper theoretical understanding of the relationship between the NTE posterior update and standard optimization algorithms (like SGD) is needed. This could unlock new optimization strategies that better mitigate catastrophic forgetting and improve continual learning performance. Ultimately, combining these directions could lead to more robust and efficient continual learning algorithms.

More visual insights

#

More on figures

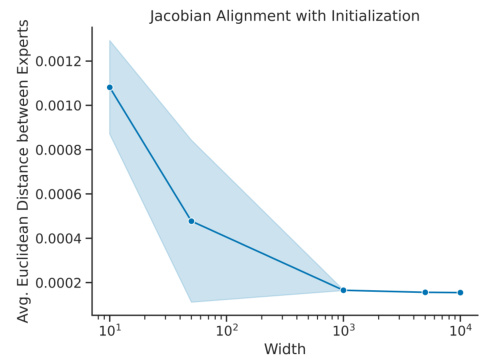
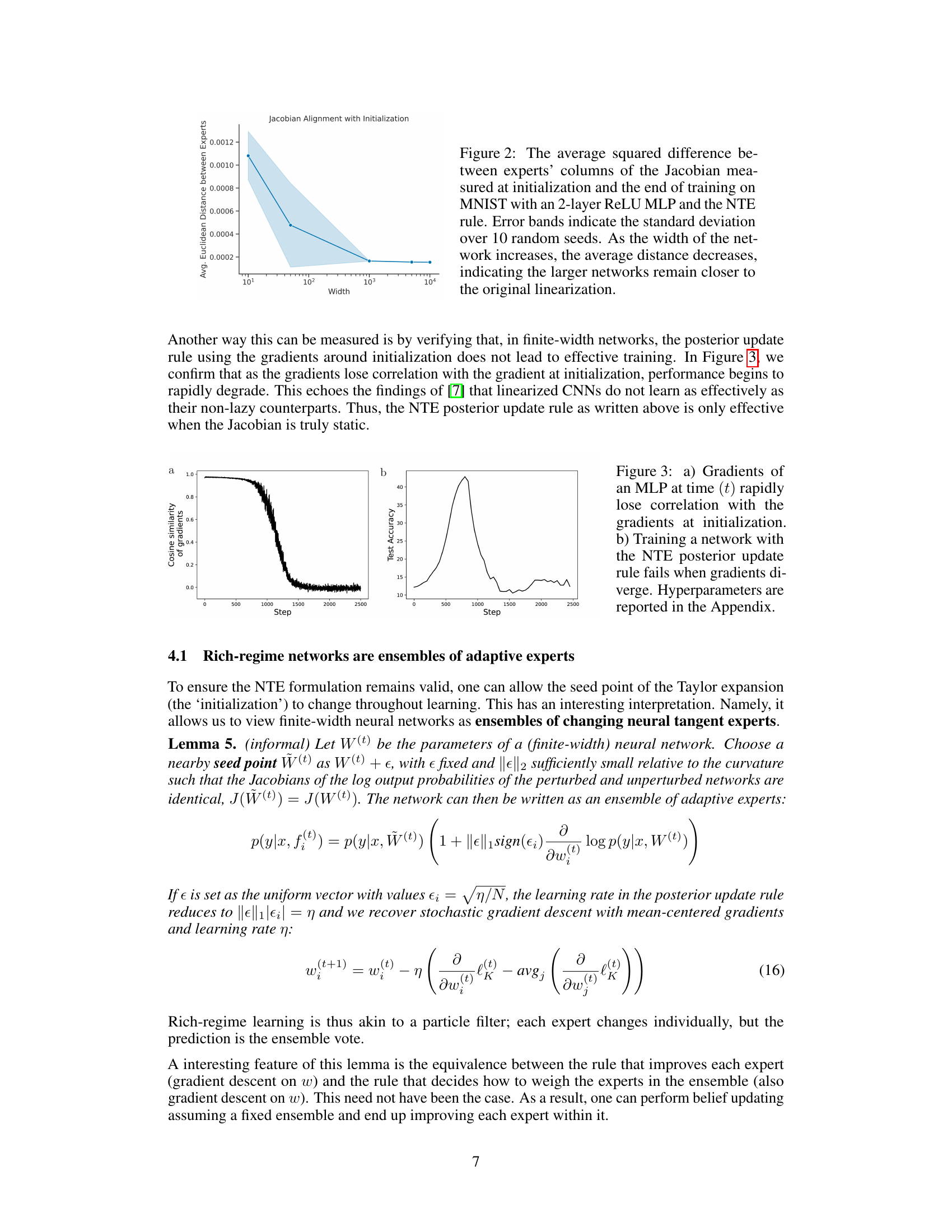
This figure shows how the average Euclidean distance between the Jacobian of the neural tangent experts at initialization and at the end of training on the MNIST dataset changes with the width of a 2-layer ReLU MLP. The results demonstrate that as network width increases, the average distance between the Jacobians decreases, indicating that wider networks maintain a closer resemblance to the original linearization used in the Neural Tangent Ensemble (NTE) approach. The error bands represent the standard deviation calculated over 10 independent random seeds.

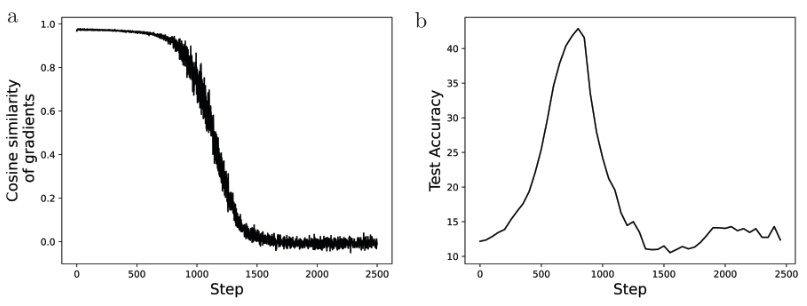
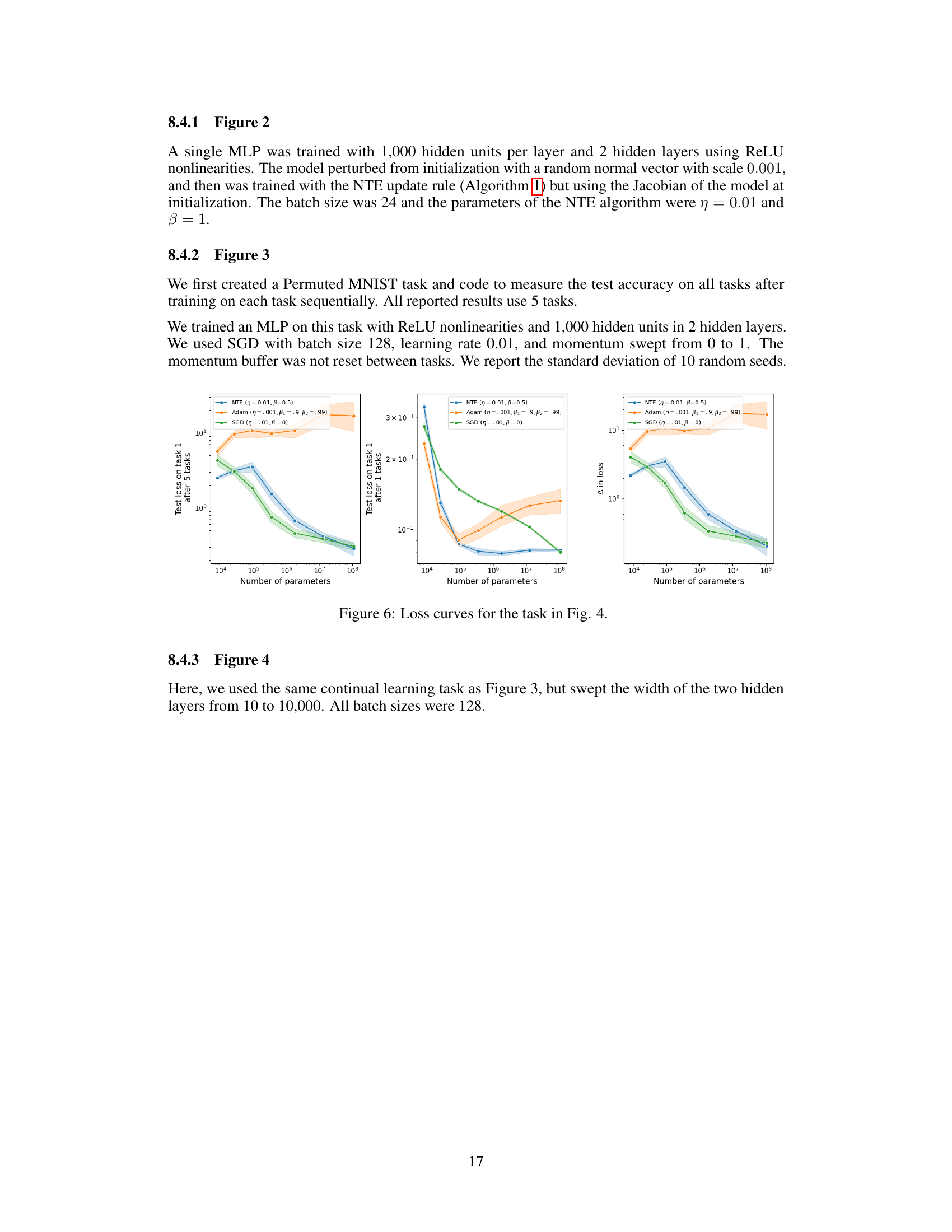
This figure shows that the gradients of a neural network trained with the Neural Tangent Ensemble (NTE) posterior update rule lose correlation with the gradients at initialization over time. This loss of correlation leads to the failure of the NTE update rule, indicating that the rule only works effectively when the network is in the ’lazy’ regime, where the Jacobian of the network does not change during training. The figure highlights a key limitation of the NTE approach and demonstrates that the assumption of fixed experts (i.e., unchanging component functions in the ensemble) does not hold in practice for networks trained with gradient descent.

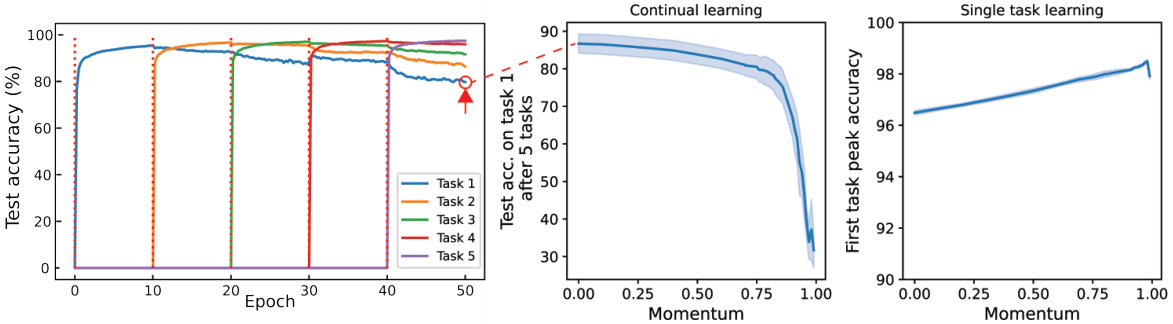
This figure shows the effect of using momentum in SGD for continual learning on the Permuted MNIST task. The left panel shows the test accuracy across 5 sequential tasks, illustrating how momentum negatively impacts the retention of previously learned information (catastrophic forgetting). The middle panel displays the test accuracy on the first task after training on all 5 tasks, while the right panel shows the peak accuracy on the first task before subsequent tasks were introduced. All panels include error bars representing standard deviations across multiple random seeds, demonstrating variability in results. The results suggest that momentum, while improving single-task performance, harms the retention of knowledge in continual learning.

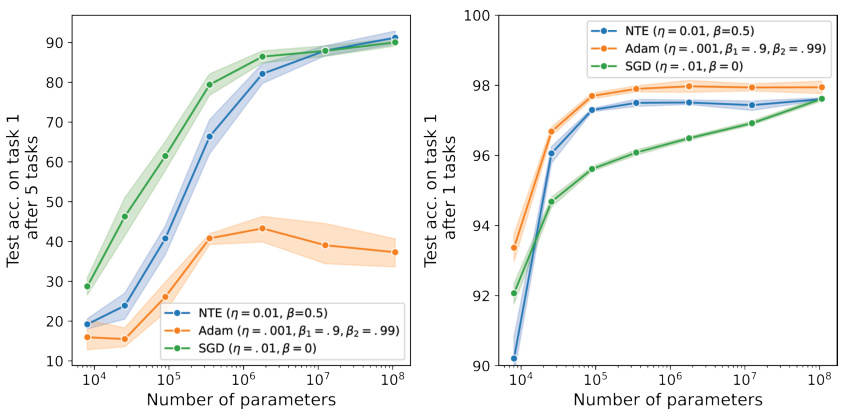
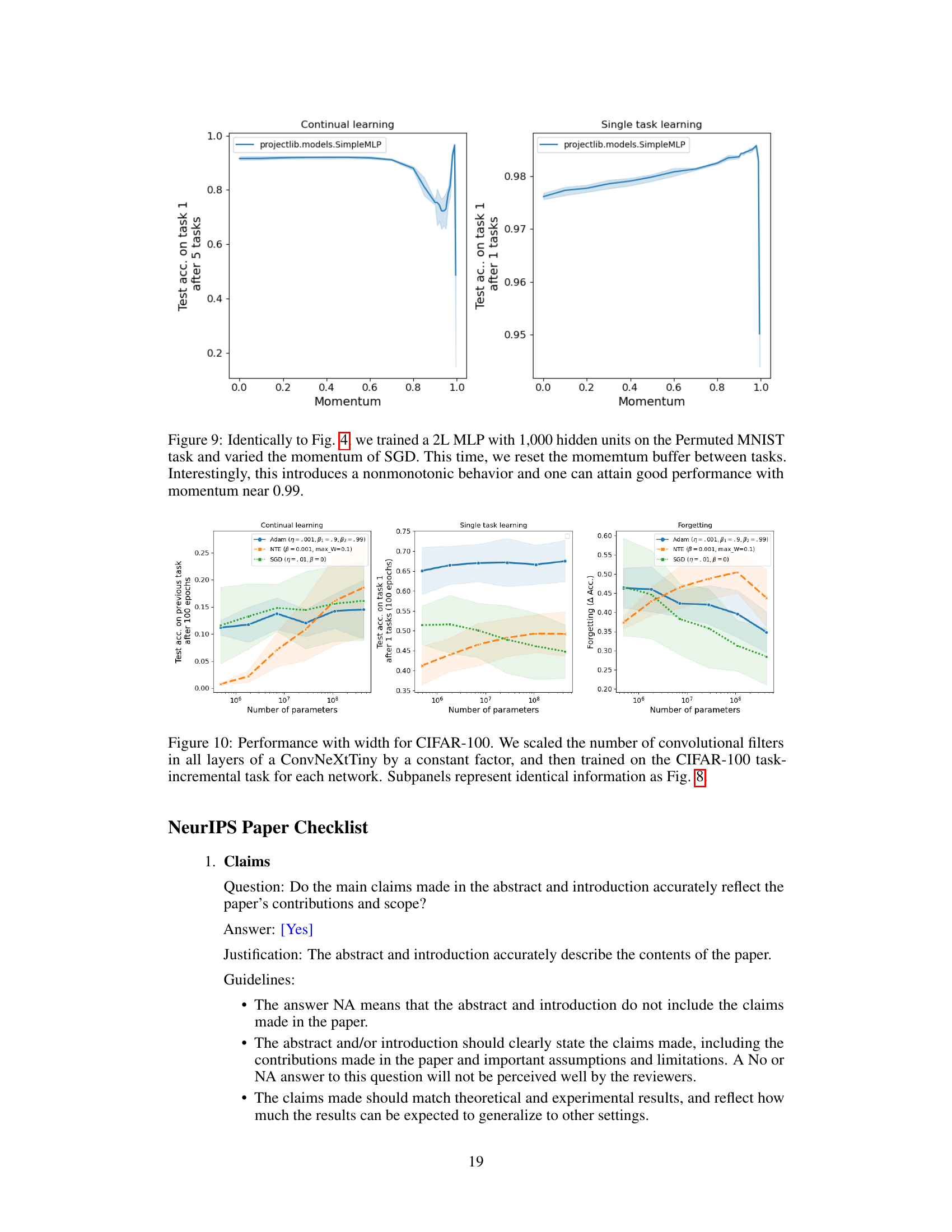
The figure shows the effect of network width on continual learning performance for three different optimizers: Neural Tangent Ensemble (NTE), Adam, and SGD. It demonstrates that wider networks generally lead to better performance in remembering previous tasks, particularly when using the NTE optimizer, while Adam shows no such improvement with wider networks.

This figure shows the test accuracy on the first task after training on 5 Permuted MNIST tasks for different network widths using three different optimizers: NTE (Neural Tangent Ensemble), Adam, and SGD (Stochastic Gradient Descent). The results demonstrate that wider networks generally lead to less forgetting (better retention of the first task’s performance), but this improvement is only observed when using the NTE optimizer. Adam shows little improvement with increasing network size, while SGD exhibits an increase in performance with width, but the increase is less substantial than the NTE optimizer.

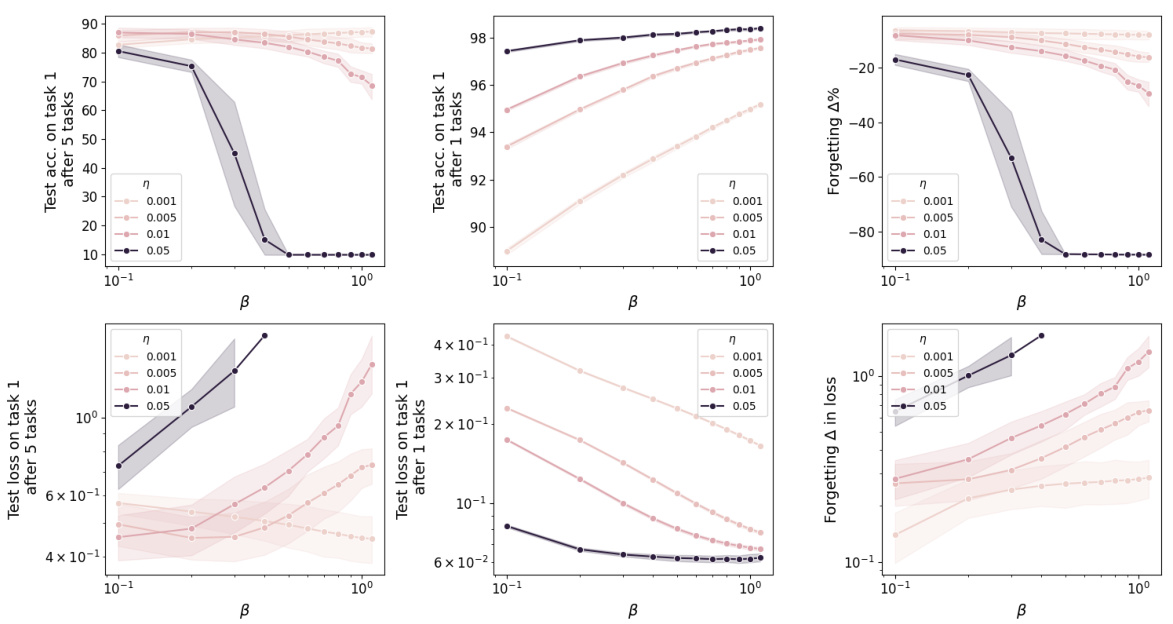
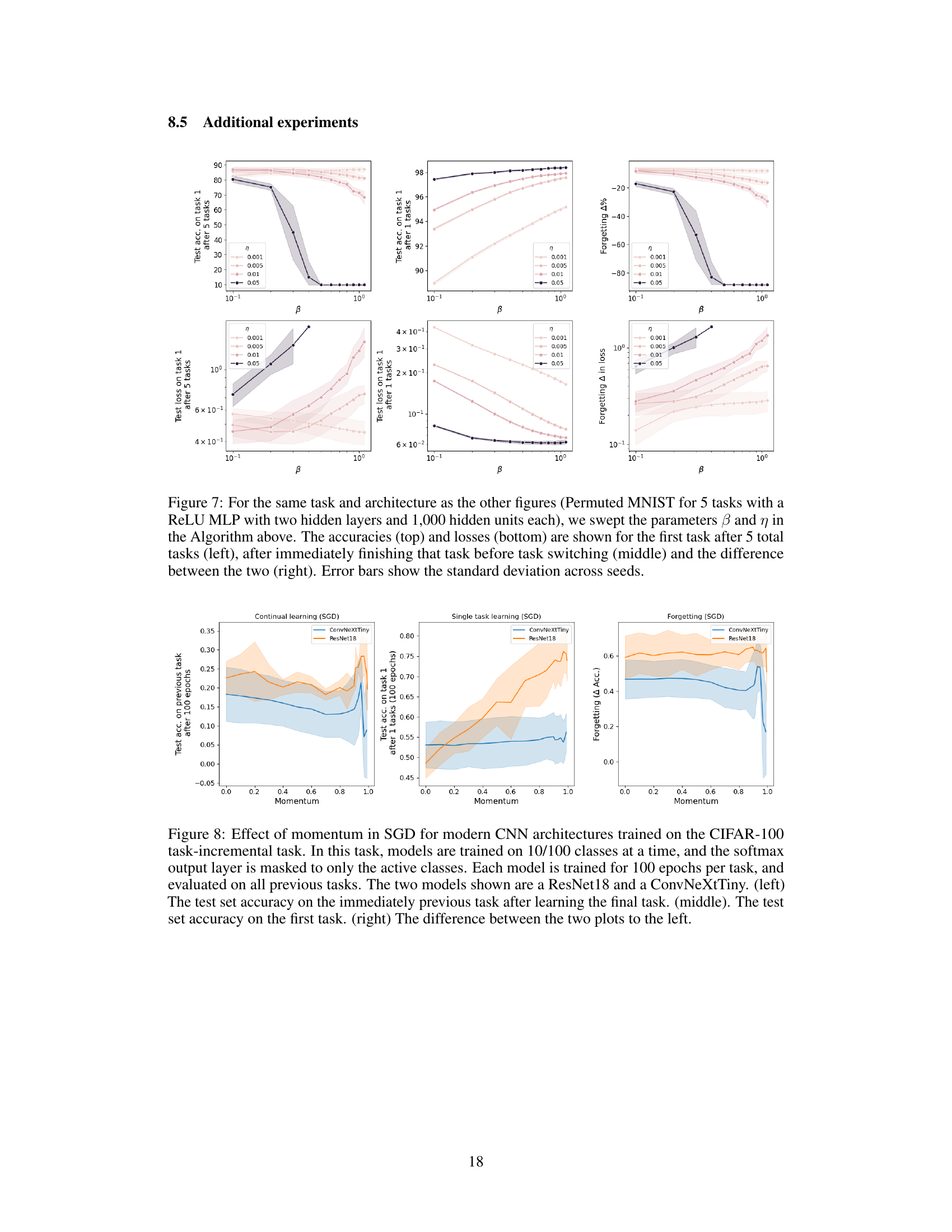
This figure shows the impact of hyperparameters β and η on the performance of the NTE update rule for the Permuted MNIST task. It displays test accuracy and loss for the first task under different scenarios: after five tasks, immediately after the first task, and the difference between these two. The results illustrate how these parameters affect the algorithm’s ability to retain knowledge of past tasks.

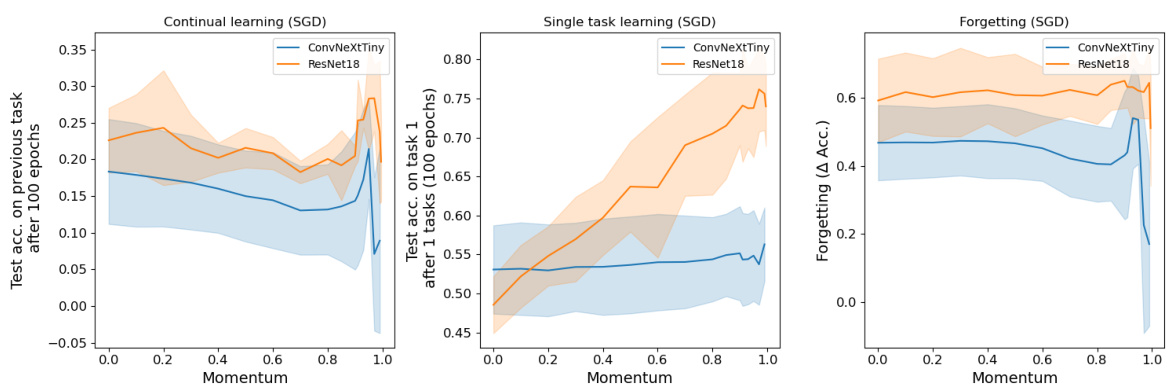
This figure shows the effect of momentum on continual learning using modern CNN architectures (ResNet18 and ConvNeXtTiny) for the CIFAR-100 task-incremental task. It displays test accuracy on the previous task and the first task, as well as the difference (forgetting), across varying momentum values. The results indicate that momentum negatively impacts continual learning performance.

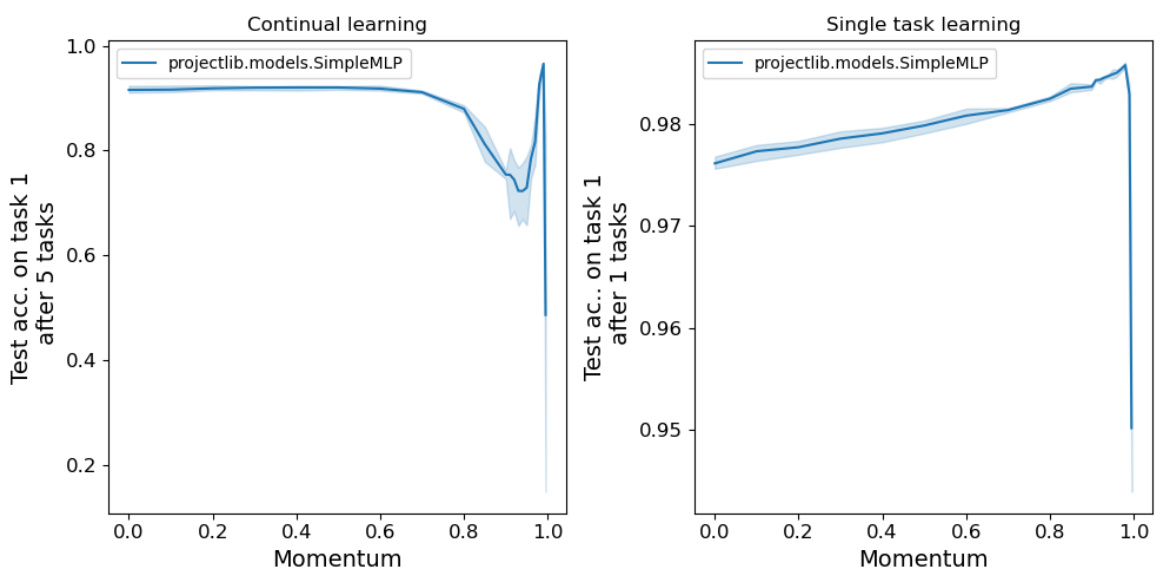
The figure shows the effect of momentum on the performance of a simple multi-layer perceptron (MLP) model trained on the Permuted MNIST task. It demonstrates how the choice of momentum significantly affects the model’s ability to remember past tasks (catastrophic forgetting). Three different plots are shown, depicting test accuracy on the first task after training on multiple sequential tasks, final test accuracy on the first task before encountering other tasks, and the difference between the two showing forgetting. It highlights the detrimental effect of using momentum in continual learning scenarios and shows that the NTE approach outperforms SGD with momentum in retaining previous knowledge.

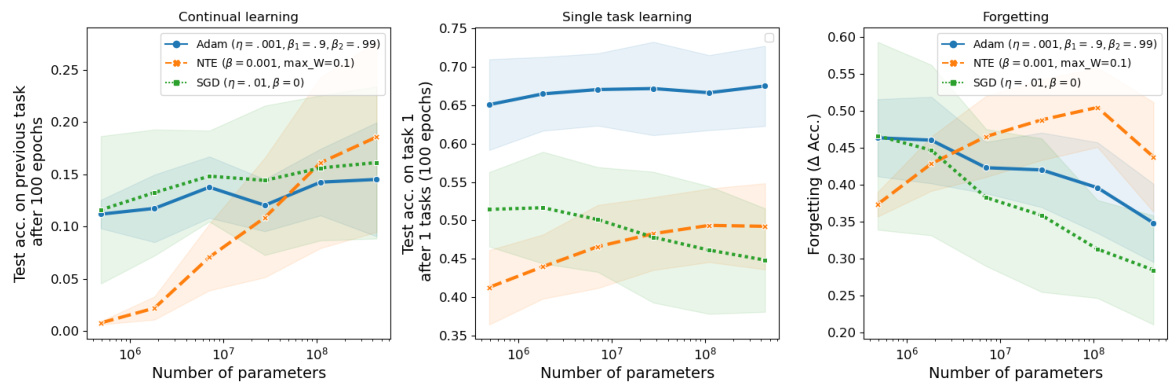
This figure shows the effect of momentum on continual learning performance using two different CNN architectures (ResNet18 and ConvNeXtTiny) on the CIFAR-100 task-incremental dataset. The experiment measures test accuracy on previous tasks after each new task is learned, as well as the drop in accuracy on the first task, demonstrating the forgetting caused by momentum.

Full paper

#