Optimal Algorithms for Online Convex Optimization with Adversarial Constraints

↗ OpenReview ↗ NeurIPS Proc. ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial because it solves a long-standing open problem in online convex optimization with adversarial constraints. It provides efficient, first-order algorithms with optimal regret and constraint violation bounds, advancing the field and enabling more practical applications. The novel analytical techniques used also have broader implications for control theory.

Visual Insights

#

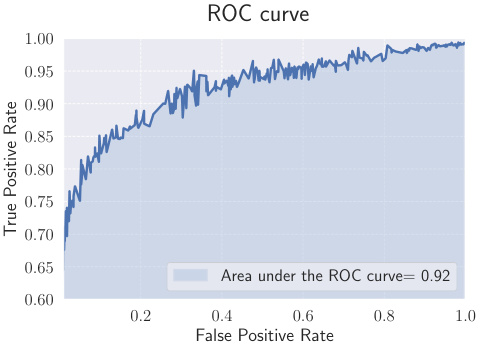
ROC curve obtained by varying the hyperparameter λ in the online credit card fraud detection experiment. The area under the curve (AUC) is approximately 0.92, indicating good performance in distinguishing between fraudulent and legitimate transactions. The x-axis represents the false positive rate (FPR), the proportion of legitimate transactions incorrectly classified as fraudulent. The y-axis represents the true positive rate (TPR), the proportion of fraudulent transactions correctly identified. A higher AUC indicates better performance.

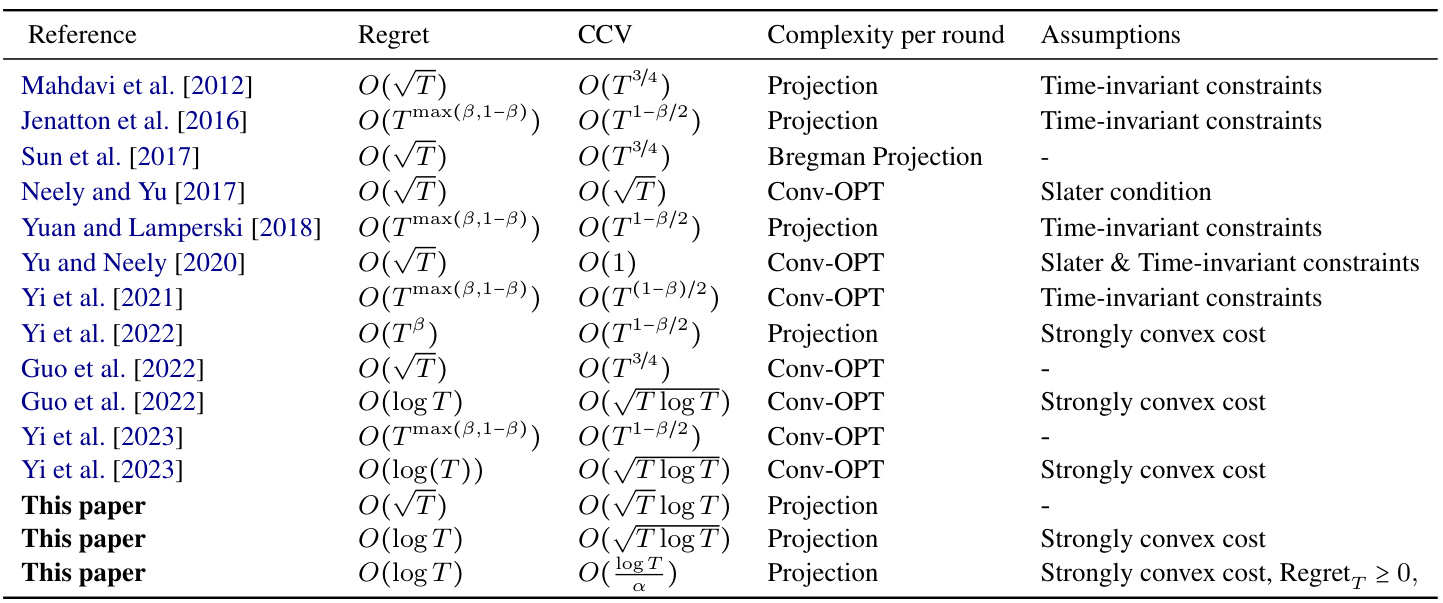
This table summarizes existing work on Constrained Online Convex Optimization (COCO), highlighting different algorithms’ regret and cumulative constraint violation (CCV) bounds under various assumptions. It compares the complexity of each algorithm per round and notes whether time-invariant constraints or strong convexity are assumed. The table concludes by showing the improved results presented in this paper.

In-depth insights

#

Adaptive COCO

#

Adaptive COCO, or Adaptive Constrained Online Convex Optimization, presents a significant advancement in online learning. It tackles the challenge of handling time-varying constraints that are revealed sequentially, making it relevant for many real-world scenarios involving uncertainty and evolving regulations. A key aspect is the algorithm’s ability to balance minimizing the cost function while simultaneously maintaining low cumulative constraint violation (CCV). This is achieved through careful design of policies that incorporate adaptive methods, allowing for efficient adjustments to changing conditions. The theoretical analysis focuses on achieving optimal regret and CCV bounds, proving the algorithm’s efficiency. Adaptive COCO algorithms are designed to be computationally efficient, often requiring only simple first-order computations at each step, making them practical for deployment in large-scale applications. The effectiveness of this approach is demonstrated through both theoretical proofs and experimental validation on real-world problems.

Regret & CCV Bounds

#

The Regret & CCV Bounds section is crucial for evaluating the performance of online convex optimization algorithms under adversarial constraints. Regret, quantifying the difference between the algorithm’s cumulative cost and that of a best-fixed action in hindsight, measures the algorithm’s performance against an optimal offline solution. CCV (Cumulative Constraint Violation) assesses the total extent to which the algorithm violates the constraints over time. The core aim is to design algorithms achieving simultaneously low regret and CCV. The paper likely presents theoretical bounds on these metrics, showing how they scale with the time horizon (T). These bounds might be expressed using Big-O notation to highlight the dominant terms as T grows large. Tight bounds are highly desirable, as they indicate that the algorithm’s performance is near-optimal. The analysis probably involves sophisticated techniques from optimization and control theory to prove these bounds. The results reveal valuable insights into the tradeoff between regret minimization and constraint satisfaction, ultimately guiding the choice of appropriate algorithms for various applications.

OCS Problem

#

The Online Constraint Satisfaction (OCS) problem, a special case of COCO, focuses solely on minimizing constraint violations without considering cost functions. This simplification allows investigation of scenarios where feasibility is not guaranteed, unlike in COCO. The OCS problem introduces a soft constraint violation metric, permitting compensation for infeasible actions in some rounds with strictly feasible actions in others. This contrasts with COCO’s hard constraint metric. Two key relaxed feasibility assumptions are explored: S-feasibility, where an admissible action exists that satisfies aggregate constraints over intervals of S rounds, and Pr-constrained adversary, where the adversary’s minimum static constraint violation is bounded. These relaxed assumptions enable the development of efficient first-order policies achieving sublinear constraint violation bounds, even in cases where the feasible set might be empty, offering a more robust framework for practical applications where perfect feasibility isn’t always attainable.

Fraud Detection

#

The research paper explores online convex optimization with adversarial constraints and applies it to fraud detection. The application focuses on imbalanced datasets, a common challenge in fraud detection where legitimate transactions vastly outnumber fraudulent ones. The proposed online learning algorithm aims to maximize the classification accuracy of fraudulent transactions while controlling for false positives. This is framed as a constrained online convex optimization problem (COCO), where the constraint represents the desired trade-off between detection rate and false alarm rate. The paper demonstrates that this approach obtains sub-linear cumulative constraint violation (CCV). This method is particularly well-suited for scenarios with sequentially revealed data and evolving constraints, as often found in real-time fraud detection systems where new data and constraints (updated rules, patterns) arrive continuously. The algorithm’s efficiency and ability to handle imbalanced data and non-convex cost functions are key strengths. The experimental results are promising, but further research could explore the algorithm’s scalability with even larger datasets and more complex feature spaces, along with a more rigorous evaluation of its performance under different types of adversarial attacks.

Future Work

#

Future research directions stemming from this work on online convex optimization with adversarial constraints could explore several promising avenues. Extending the framework to handle bandit feedback where the learner doesn’t directly observe the cost function but only receives a noisy reward would significantly broaden the applicability of the results. Another exciting path involves developing adaptive algorithms that are both computationally efficient and theoretically optimal without strong assumptions like Slater’s condition, focusing on methods that scale well to high-dimensional settings. Investigating the dynamic regret setting where the benchmark is time-varying would be valuable for more realistic scenarios. Finally, a deeper dive into the practical implications and applications of the proposed algorithms in specific domains like fraud detection or resource allocation could significantly enrich the understanding and impact of the research. Further theoretical investigation into the tightness of the derived bounds and exploration of alternative potential functions would also contribute to the field. The exploration of these diverse aspects could lead to substantial advancements in this crucial area of machine learning.

More visual insights

#

More on figures

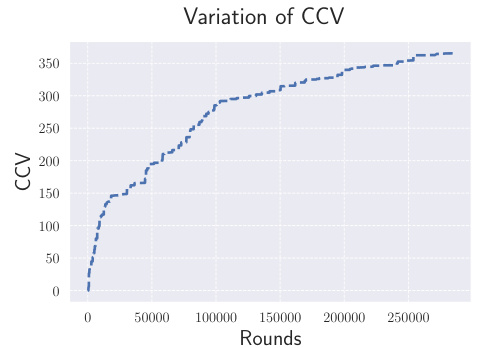
This figure shows how the cumulative constraint violation (CCV) changes over time (number of rounds). The CCV increases, but at a sublinear rate, indicating the effectiveness of the proposed online policy in controlling constraint violations, even with an adaptive adversary.

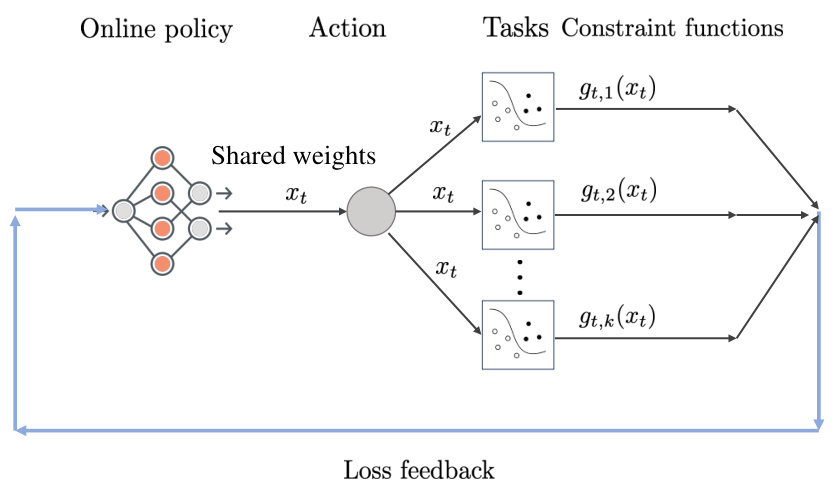
This figure illustrates the online multi-task learning problem. An online policy selects an action (shared weights, xt) that is used to perform multiple related tasks. After the action is chosen, the adversary reveals constraint functions (gt,i(xt)) for each task, representing the loss or error associated with that task. The goal is to minimize the cumulative constraint violation, where a task is considered successful if the corresponding constraint is satisfied (i.e., loss is non-positive).

Full paper

#