What type of inference is planning?

↗ OpenReview ↗ NeurIPS Proc. ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is vital for researchers in AI planning because it clarifies the ambiguity surrounding different inference types used in planning-as-inference approaches and introduces a novel variational framework for planning that is applicable to various planning problems. This framework not only enhances understanding but also opens avenues for developing more efficient and effective planning algorithms.

Visual Insights

#

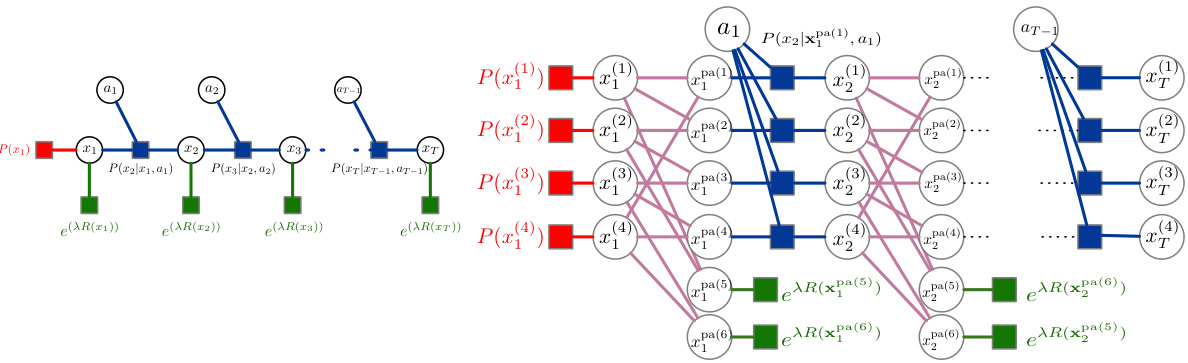
This figure displays two factor graphs representing Markov Decision Processes (MDPs). The left graph shows a standard MDP, where all states and actions are explicitly represented. The right graph illustrates a factored MDP, which breaks down the state space into smaller, interacting components. This factorization allows for a more compact representation but introduces dependencies between the factors, indicated by the sparse connectivity. The figure highlights the difference in representation complexity between standard and factored MDPs, with factored MDPs offering potential advantages for scalability in large state spaces, even though they introduce computational challenges related to approximate inference.

This table summarizes various inference types from a variational perspective. It shows the closed-form expression for the quantity of interest, the corresponding entropy term in the variational bound, and whether a closed-form solution is tractable for Markov Decision Processes (MDPs). The table highlights the differences between various inference types such as Marginal, Planning, M. MAP, MAP, and Marginal and clarifies the relationship between them.

In-depth insights

#

Planning as Inference

#

The “Planning as Inference” paradigm recasts planning problems as probabilistic inference tasks. This approach leverages the powerful tools of probabilistic graphical models, enabling the use of techniques like belief propagation and variational inference to solve planning problems. A core idea is to represent the planning problem as a factor graph, where factors encode the transition probabilities, rewards, and policies. This allows for the application of various inference methods, each with its own strengths and weaknesses. The choice of inference method significantly impacts the computational tractability and the quality of the resulting plans, particularly under different levels of stochasticity in the environment. The authors highlight that ‘planning’ itself constitutes a distinct inference type, different from commonly used methods such as marginal, MAP, or MMAP inference. They demonstrate empirically that their proposed method, based on a novel variational formulation of planning, is superior to existing methods in scenarios with moderately high stochasticity. The variational framework provides a unifying perspective for understanding the relationship between different inference types and their suitability for planning. The empirical evaluation showcases that the proposed technique outperforms state-of-the-art approaches on benchmark planning problems.

Variational Planning

#

Variational planning presents a novel perspective on planning as inference by framing it within a variational framework. This approach elegantly connects various inference types (e.g., marginal, MAP) to different weightings of entropy terms in the variational problem. Planning itself emerges as a distinct inference type with its own unique weighting, enabling the application of variational inference techniques such as loopy belief propagation to approximate planning in complex, factored state Markov Decision Processes. This approach demonstrates that previously employed inference methods for planning are only suitable under low stochasticity, highlighting the importance of the variational perspective in handling stochastic environments. The framework also allows for a closed-form determinization, providing a tractable approach to solving deterministic planning problems, even in high-dimensional factored spaces. This unification simplifies and extends the capabilities of existing variational inference methods and presents a comprehensive perspective on the relationship between different inference types and planning in stochastic domains.

Factored MDPs

#

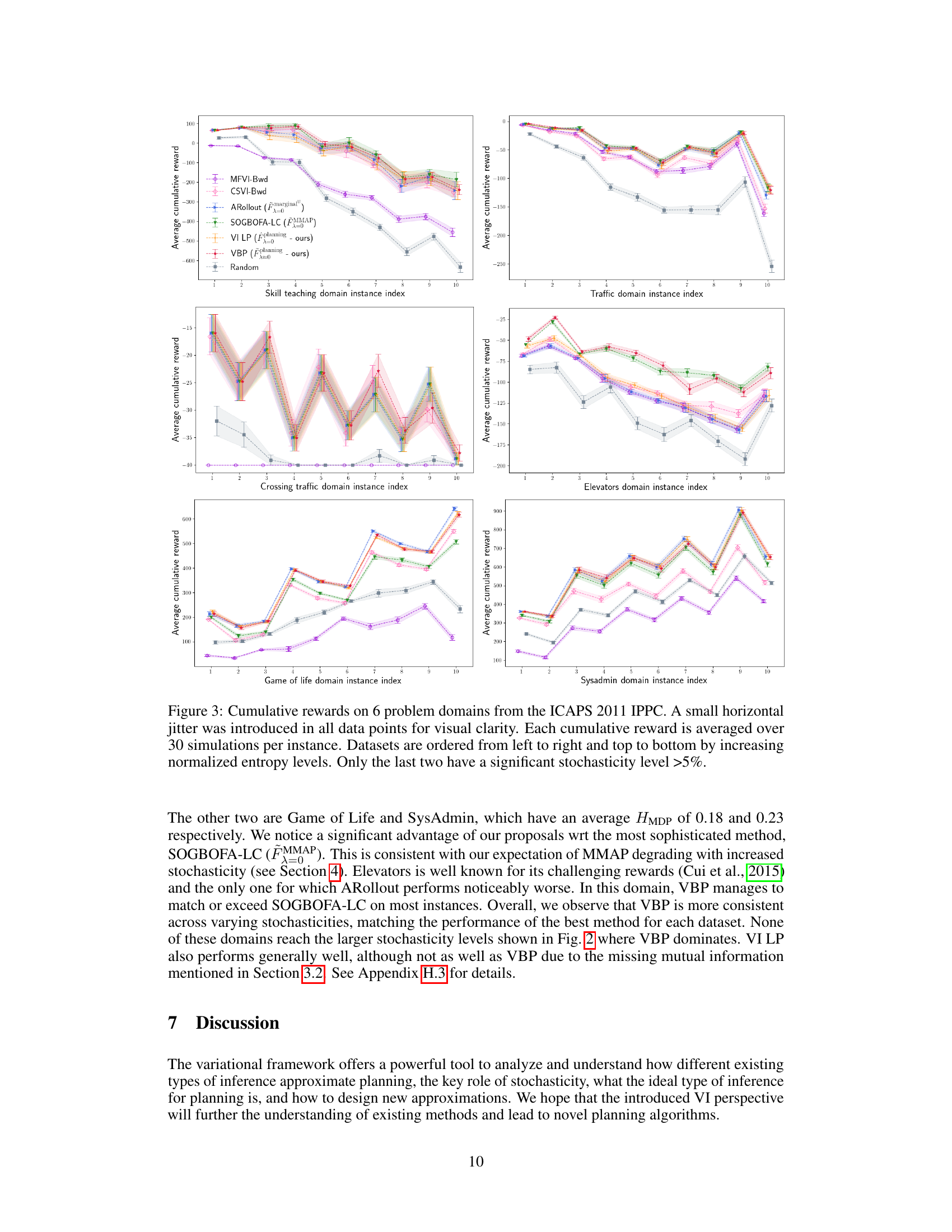
Factored Markov Decision Processes (MDPs) offer a way to address the computational complexity inherent in standard MDPs, particularly when dealing with high-dimensional state spaces. By assuming that the state can be decomposed into a set of interacting, lower-dimensional factors, the factored MDP approach dramatically reduces the computational burden associated with solving for optimal policies. This decomposition allows for more efficient algorithms to be used, such as loopy belief propagation (LBP), adapted in the paper to value belief propagation (VBP) to handle the planning inference task. However, the effectiveness of factored MDPs relies heavily on the structure of the problem and the choice of factorization. Poorly chosen factorizations can negate the computational gains, and the resulting approximate inference techniques (like VBP) may lead to suboptimal solutions, especially in scenarios with high stochasticity in the dynamics. The paper’s main contribution is to reveal the planning task as a distinct type of inference problem, which can be solved by adapting methods designed for solving standard inference problems, making the entire body of such techniques applicable. This approach is validated empirically by comparing its performance to other methods that have been used for planning as inference.

VBP Algorithm

#

The Value Belief Propagation (VBP) algorithm, as presented in the research paper, is a novel approximate inference method designed for planning in factored Markov Decision Processes (MDPs). It leverages the variational inference framework and addresses the challenge of exponentially large state spaces inherent in factored MDPs. Unlike previous approaches, VBP directly tackles planning as a distinct inference problem, avoiding the limitations of marginal, MAP, or MMAP inference in stochastic environments. By introducing a Bethe approximation to the entropy term and employing a loopy belief propagation-like message passing scheme, VBP achieves tractability while maintaining accuracy. This makes VBP suitable for handling complex, real-world problems with many interacting variables. The algorithm’s key strength lies in its variational foundation, allowing for a principled comparison to other inference types and potentially offering improved performance in moderately stochastic settings. The empirical results demonstrate VBP’s competitive performance against existing state-of-the-art methods. Further research could explore refinements of the Bethe approximation, adaptive message scheduling strategies, and alternative optimization techniques to further enhance its efficiency and convergence properties.

Inference Ranking

#

The concept of ‘Inference Ranking’ in the context of planning as inference is crucial. It involves comparing the performance of different probabilistic inference methods (e.g., marginal, MAP, MMAP) when applied to planning problems. The paper likely demonstrates a hierarchical relationship among these methods, highlighting the scenarios where one method outperforms another. This ranking is highly dependent on the level of stochasticity present in the system’s dynamics. In deterministic environments, MAP or MMAP might be optimal, while with increased stochasticity, a specialized ‘planning inference’ approach might be superior. The key insight lies in understanding the trade-off between computational complexity and accuracy. While methods like MMAP offer theoretically better bounds, they are often intractable. The paper likely proposes an alternative that balances accuracy with computational feasibility by cleverly weighting entropy terms within a variational inference framework. This highlights the importance of choosing an appropriate inference method based on the characteristics of the specific planning problem.

More visual insights

#

More on figures

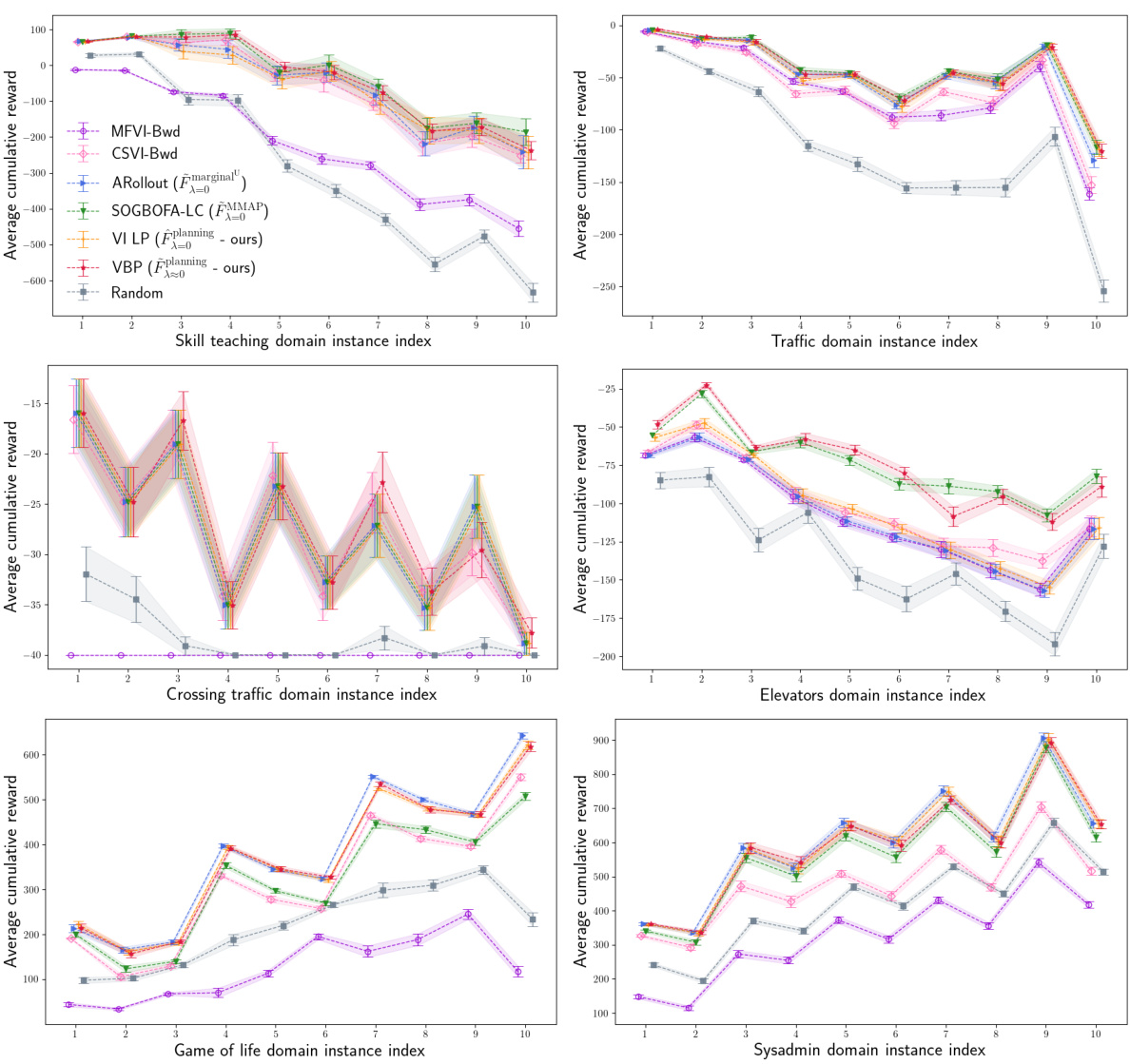
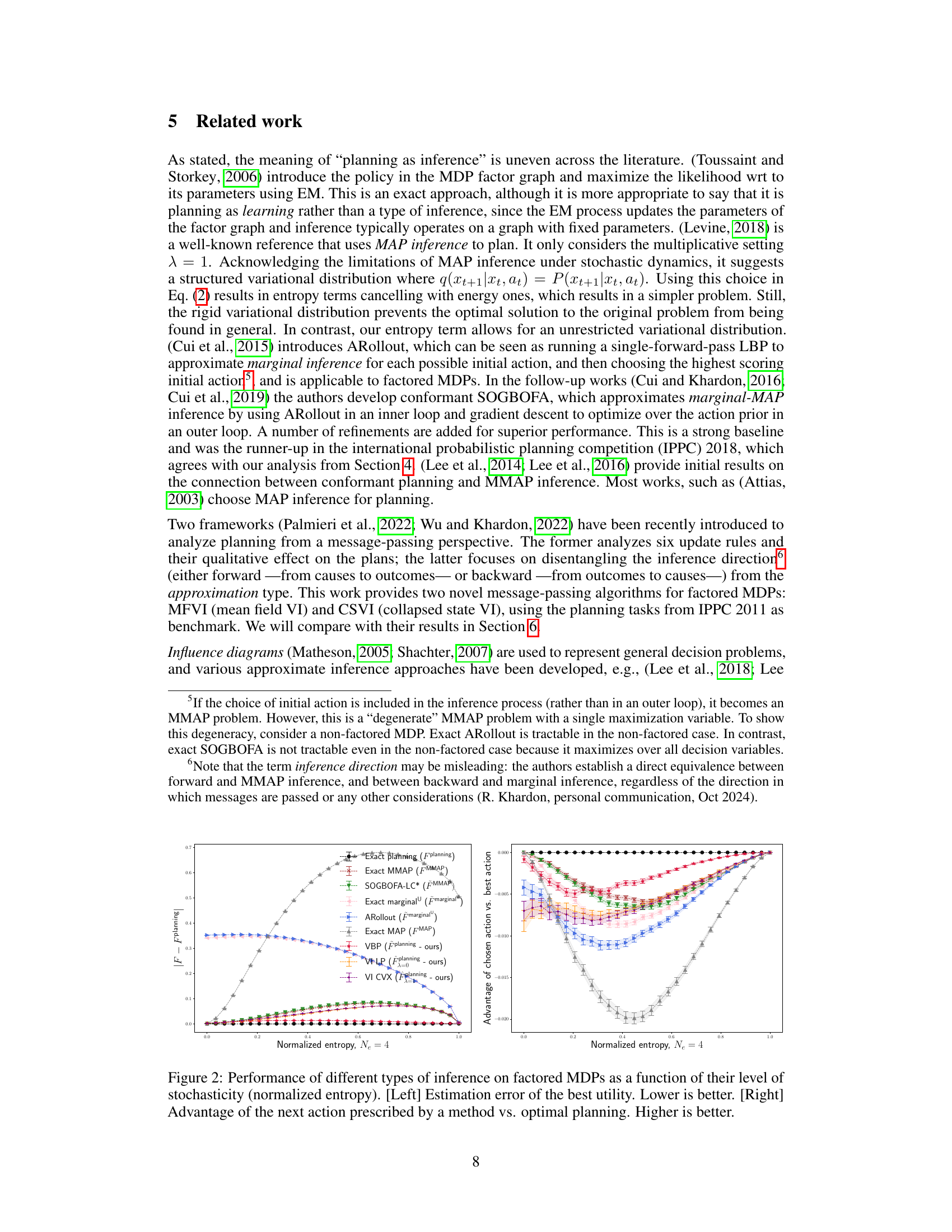
This figure compares the performance of different inference methods (MFVI-Bwd, CSVI-Bwd, ARollout, SOGBOFA-LC*, exact marginal, exact MAP, exact MMAP, exact planning, VBP, VI LP) on factored Markov Decision Processes (MDPs) with varying levels of stochasticity. The left panel shows the estimation error of the best utility, where lower values indicate better performance. The right panel shows the advantage of the action chosen by each method compared to the optimal planning action, with higher values indicating better performance. The x-axis represents the normalized entropy, a measure of stochasticity.

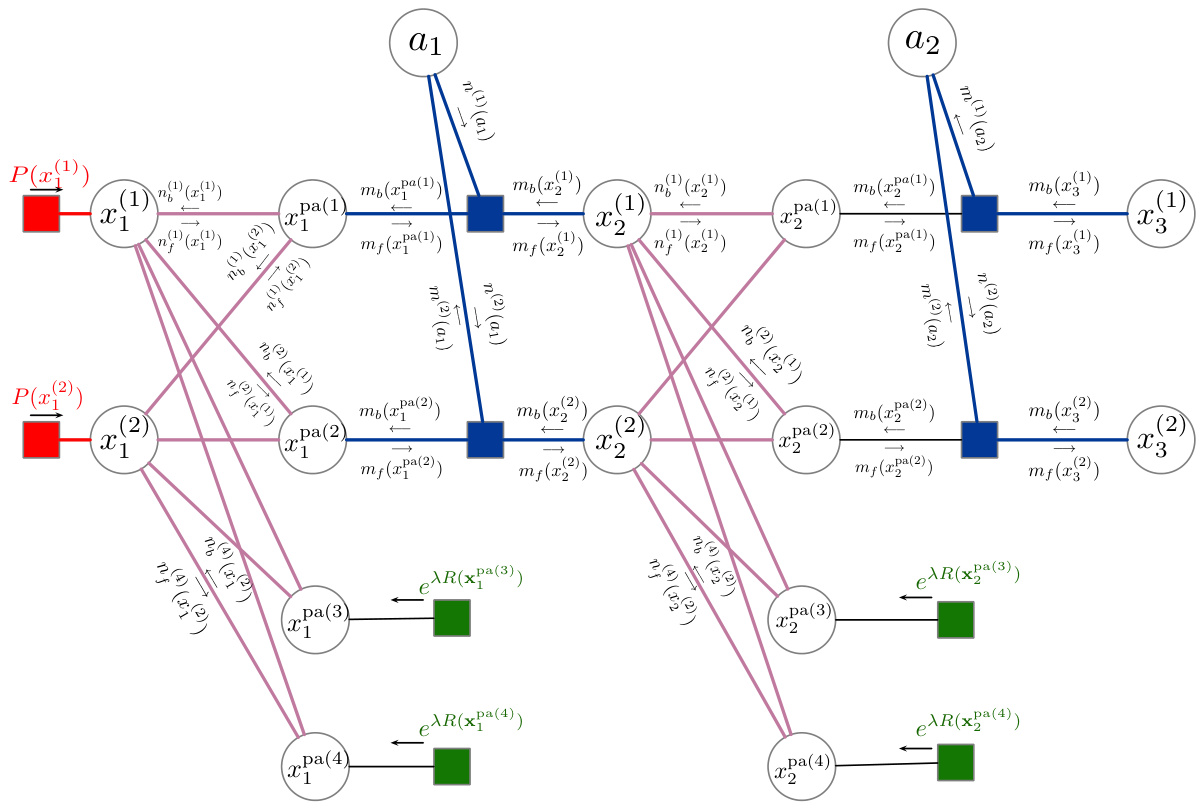
This figure illustrates the correspondence between the message-passing updates used in the Value Belief Propagation (VBP) algorithm and the factor graph representation of a factored Markov Decision Process (MDP). It visually connects the messages (m, n, and b) exchanged between factor nodes during VBP with the variables and factors within the factored MDP. This helps clarify the relationship between the approximate inference algorithm and the underlying probabilistic model.

Full paper

#