↗ OpenReview ↗ NeurIPS Proc. ↗ Chat
TL;DR#
Online convex optimization often struggles with non-stationary problems. Existing methods for handling this, using switching regret as a measure, either had suboptimal regret bounds or were computationally expensive. The challenge is to find an algorithm that minimizes cumulative loss, accounting for changes in the optimal action over time.
The paper introduces the RESET algorithm. RESET cleverly uses a recursive tree structure and an adaptive base algorithm to achieve the asymptotically optimal switching regret simultaneously for every possible segmentation. Its efficiency is another highlight, with logarithmic space and per-trial time complexity. Furthermore, it provides novel bounds on dynamic regret, showing its adaptability to changing conditions. These results represent a significant advancement in online convex optimization, addressing existing limitations and proposing a novel, parameter-free and efficient solution.
Key Takeaways#
Why does it matter?#
This paper is crucial because it offers an efficient algorithm that achieves the asymptotically optimal switching regret across all possible segmentations. This significantly improves upon previous methods that were either suboptimal or computationally expensive, opening up new avenues for online convex optimization in non-stationary settings.
Visual Insights#
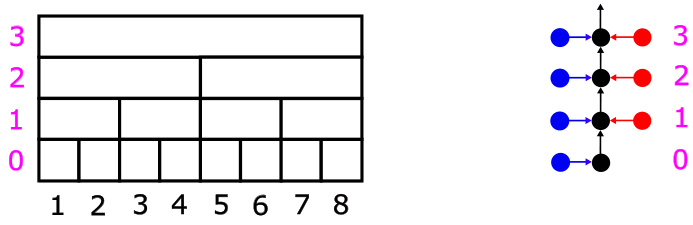
The figure illustrates the RESET algorithm with 8 trials. The left panel shows how the base actions and mixing weights are generated for each level and trial. Each level runs an instance of the base algorithm, and the mixing weights are reset at the start of each segment (whose length determines how the mixing weights update). The right panel shows how the algorithm computes the action xt on trial t using a combination of base actions, mixing weights, and propagating actions.

The algorithm RESET (Recursion over Segment Tree) is presented. It uses a base algorithm for online convex optimisation, along with a mixing weight for each level in a segment tree to achieve the asymptotically optimal switching regret simultaneously across all possible segmentations.
Full paper#



















