↗ OpenReview ↗ NeurIPS Proc. ↗ Chat
TL;DR#
Many machine learning problems can be formulated as variational inequalities (VIs). Existing high-order methods for VIs demand precise derivative computations, which can be computationally expensive. This often limits their applicability to large-scale machine learning tasks where exact derivatives are unavailable or too costly to compute. Furthermore, existing high-order methods typically lack theoretical guarantees of global convergence.
This work addresses these challenges by introducing VIJI, a novel second-order method for solving VIs with inexact Jacobian information. The researchers establish lower bounds and demonstrate that their method attains optimal convergence rates in the smooth and monotone VI setting when derivative approximations are sufficiently accurate. They also propose quasi-Newton updates to make VIJI more practical, achieving a global sublinear convergence rate even with inexact derivatives. Finally, the method is generalized to handle high-order derivatives.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working on variational inequalities, especially in machine learning. It provides optimal algorithms that are robust to common issues like inaccurate Jacobian calculations, a significant improvement over existing methods. The global convergence rate analysis and lower bounds established provide a strong theoretical foundation for future advancements in the field, paving the way for more efficient and practical algorithms.
Visual Insights#
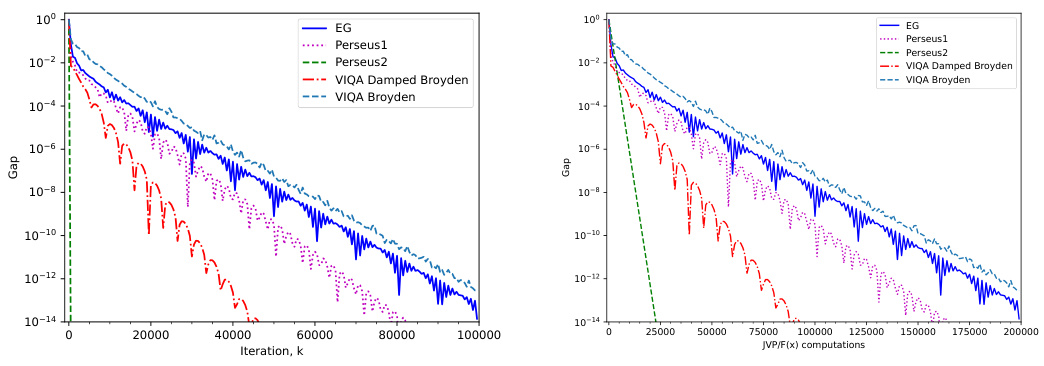
This figure compares the performance of different optimization methods for solving a cubic regularized bilinear min-max problem. The methods compared are Extragradient (EG), first-order Perseus (Perseus1), second-order Perseus with Jacobian (Perseus2), VIQA with Damped Broyden approximation, and VIQA with Broyden approximation. The left plot shows the gap (a measure of optimality) versus the iteration number, while the right plot shows the gap versus the number of Jacobian-vector product (JVP) or function evaluations. The results demonstrate that the second-order methods (Perseus2 and VIQA variants) converge significantly faster than the first-order methods (EG and Perseus1), and that VIQA with Damped Broyden approximation exhibits the fastest convergence.
Full paper#