Learning Generalized Linear Programming Value Functions

↗ OpenReview ↗ NeurIPS Proc. ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial for researchers in large-scale optimization because it presents a novel, efficient method for approximating the Generalized Linear Programming Value Function (GVF). This significantly speeds up algorithms for solving complex, two-stage mixed-integer linear programs (MILPs), a common challenge in various fields. Its unsupervised learning approach avoids costly LP solutions during training, offering a significant advantage in scalability. The work also introduces a new neural network architecture tailored for GVFs, pushing the boundaries of value function approximation. Furthermore, the method offers a fast heuristic for large-scale MILPs, proving useful in diverse applications.

Visual Insights

#

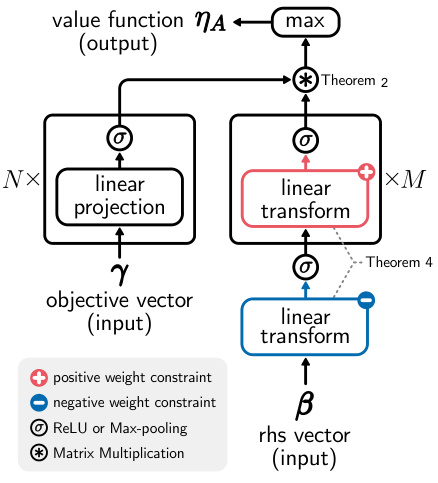
The Dual-Stack Model (DSM) is a neural network architecture for approximating the Generalized Linear Programming Value Function (GVF). It consists of two stacks of feedforward neural networks: a γ-stack (for objective vectors) and a β-stack (for constraint bounds). Each stack uses piecewise linear activation functions (ReLU or Max-pooling). The β-stack enforces input convexity by using non-positive weights in the first layer and non-negative weights in subsequent layers. The output is the maximum element of the dot product between the outputs of the γ-stack and β-stack, mimicking the GVF’s structure as a maximum of bilinear functions. The model is designed for unsupervised learning, avoiding the need to solve LPs during training.

This table compares the performance of the Dual-Stack Model (DSM) and DenseNet in learning the Generalized Linear Programming Value Function (GVF). It shows the training time, true relative error (the difference between the model’s approximation and the true GVF, relative to the maximum of the two), and the percentage of constraints satisfied for both training and testing sets. The results are broken down by different GVF instance families (KG and Euclidean) and sizes, highlighting the scalability and accuracy of the methods. It demonstrates that the unsupervised DSM approach performs comparably or better than the supervised DenseNet approach in approximating the GVF, despite not requiring labeled data.

In-depth insights

#

GVF Learning

#

The GVF learning section likely details a novel machine learning approach for approximating Generalized Linear Programming Value Functions (GVFs). This likely involves designing a neural network architecture tailored to the specific mathematical properties of GVFs, such as convexity and piecewise linearity. The training methodology is crucial; the authors may explore supervised, unsupervised, or semi-supervised techniques, each with its own advantages and disadvantages regarding data requirements and computational cost. A key innovation might be an unsupervised learning method that avoids the computationally expensive step of solving linear programs for each data point. The evaluation likely focuses on the accuracy of the learned GVF approximation and its performance in solving related optimization problems. The authors may demonstrate improved efficiency or solution quality compared to traditional methods, highlighting the benefits of their approach for handling large-scale problems. The discussion of limitations and future directions could include challenges such as training stability, generalization to unseen problem instances, and handling high-dimensional data.

Dual-Stack Model

#

The Dual-Stack Model, proposed for approximating the Generalized Linear Programming Value Function (GVF), is a novel neural network architecture. Its key innovation lies in its two independent stacks mirroring the GVF’s structural properties: a ‘y-stack’ processing objective coefficients and a ‘β-stack’ handling constraint bounds. This mirrored design directly encodes the bilinear nature of the GVF within invariancy regions. Each stack utilizes piecewise linear activation functions, ensuring the model’s output preserves this crucial piecewise linearity, critical for efficient optimization. The unsupervised learning method paired with the DSM is particularly noteworthy, eliminating the computationally expensive LP solves required for data generation in supervised approaches. The weight constraints in the β-stack further enhance the model by enforcing input convexity, aligning with the GVF’s inherent properties and facilitating efficient optimization. The DSM’s ability to learn a compact representation of the GVF highlights its potential for significantly speeding up large-scale optimization problems.

MILP Heuristic

#

The proposed MILP heuristic leverages a learned Generalized Linear Programming Value Function (GVF) to accelerate the solution process for two-stage mixed-integer linear programs (MILPs). The core idea is to replace computationally expensive second-stage subproblems with their approximated GVF counterparts. This approximation is obtained through an unsupervised machine learning approach, avoiding the cost of repeatedly solving LPs to generate training data. The resulting reformulation is a compact LP amenable to efficient optimization techniques, particularly beneficial for large-scale MILPs. This approach offers a trade-off between solution quality and computational speed. While the GVF provides a guaranteed lower bound, the heuristic’s practical performance hinges on the accuracy of the GVF approximation learned via the dual-stack neural network architecture. The heuristic’s effectiveness depends on the balance between learning complexity and the degree to which the GVF accurately models the original MILP. Empirical evaluations suggest the heuristic often outperforms traditional Benders decomposition for challenging large-scale problems. Further enhancements to the training methodology and GVF approximation could improve its overall performance and extend its applicability to broader classes of MILPs.

Unsupervised Training

#

The concept of unsupervised training within the context of learning generalized linear programming value functions is a significant contribution. It eliminates the need for expensive and time-consuming data generation, a common bottleneck in supervised approaches. This is achieved by leveraging a constrained optimization problem whose solution uniquely defines the GVF. The method’s unsupervised nature makes it more scalable and practical for large-scale applications where obtaining labeled data from LP solutions is computationally prohibitive. The use of a penalty term in the optimization problem to softly enforce the constraints ensures that the model learns a valid under-approximation of the GVF, even without explicit labeled data, this under-approximation property is crucial for using the learned model in subsequent optimization problems. This makes the unsupervised learning framework particularly valuable, not only for its efficiency, but also for its potential to unlock applications of value function approximation in settings where labeled data is scarce or costly.

Future Work

#

The authors suggest two primary avenues for future research. First, they propose improving the training objective function by finding a more stable balance between data fitting and constraint satisfaction. This could involve exploring alternative penalty functions or more sophisticated optimization techniques. Addressing the instability in the current approach is crucial to enhance the reliability and robustness of the GVF learning method. Second, they aim to improve the model’s generalization to unseen objective vectors by either increasing the training data size or developing a more effective approach for handling the constraints. This will be important for broader applicability of the model in real-world scenarios, where it may be infeasible or impractical to obtain complete data beforehand. Both of these suggestions focus on improving core aspects of the proposed methodology, indicating a thoughtful and systematic plan for future developments.

More visual insights

#

More on tables

This table compares the performance of the Dual-Stack Model and DenseNet in learning the Generalized Linear Programming Value Function (GVF). It shows the training time, true relative error (the difference between the model and the actual GVF), and the percentage of constraints satisfied (a measure of how well the model approximates the GVF) for different model sizes and instance types. The table also provides data labelling times for the DenseNet for comparison. This allows assessment of the relative computational costs involved.

This table compares the performance of the Dual-Stack Model and DenseNet in learning the Generalized Linear Programming Value Function (GVF). It shows the training time, true relative error (a measure of approximation accuracy), and the percentage of constraints satisfied during training and testing for both models across different problem instances (KG and Euclidean). The table also includes the time taken to generate labels (data labeling time) for the supervised learning models. This illustrates the scalability of the DSM approach and its comparison against alternative methods.

This table compares the performance of the Dual-Stack Model and DenseNet in learning the Generalized Linear Programming Value Function (GVF). It shows the training time, true relative error, and percentage of constraints satisfied for both models on various instances of the uncapacitated facility location problem. The table also provides data labeling times for the supervised methods (DenseNet and Random Forest). The results indicate that the Dual-Stack Model can perform comparably to or better than the supervised methods, even without labeled data, demonstrating its efficiency in learning the GVF.

This table compares the performance of the proposed DSM heuristic against a state-of-the-art MILP solver (SCIP) and a Benders decomposition heuristic on Uncapacitated Facility Location (UFL) instances. For each instance size (250, 500, 750 for KG instances; 100, 200, 300 for Euclidean instances), it reports the solve time, provable gap (%), gap to MILP (%), and gap to Benders for the DSM heuristic, as well as LP relaxation solve time, MILP solve time, and solve time for the full model and Benders heuristic, respectively. Negative values in ‘Gap to MILP (%) ’ indicate the DSM heuristic outperformed SCIP within the time limit.

This table compares the performance of the Dual-Stack Model and DenseNet in learning the Generalized Linear Programming Value Function (GVF). It shows the training time, true relative error, training lower bound, test lower bound, and data labeling time for both models on a specific SCFL instance (16 customers, 50 facilities). The true relative error indicates the accuracy of the learned GVF approximation. The lower bounds reflect the percentage of constraints satisfied during training and testing.

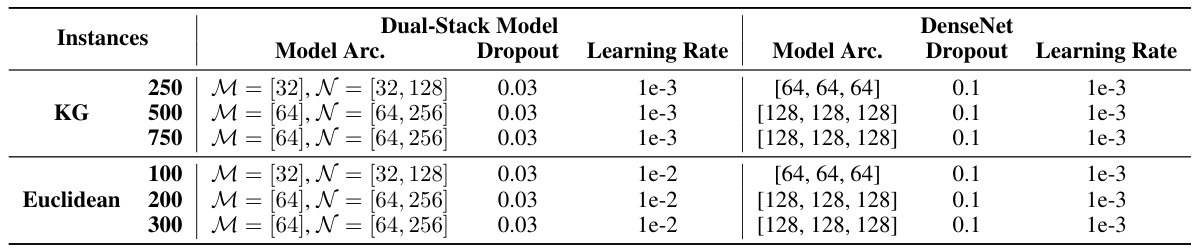
This table compares the performance of the Dual-Stack Model (DSM) and DenseNet in learning the Generalized Linear Programming Value Function (GVF). It shows the training time, true relative error (a measure of approximation accuracy), and the percentage of constraints satisfied during training and testing for various instances of the uncapacitated facility location (UFL) problem. The results indicate how well each model approximates the GVF, considering both training efficiency and approximation quality.

This table compares the performance of the Dual-Stack Model and DenseNet in learning the Generalized Linear Programming Value Function (GVF). It shows the training time, true relative error (the percentage difference between the model’s prediction and the true GVF), and the percentage of constraints satisfied during training for both models across different sizes of instances (KG and Euclidean). The results indicate the Dual-Stack Model’s competitiveness in approximating the GVF, particularly considering that it does not use supervised training.

This table compares the performance of the Dual-Stack Model and DenseNet in learning the Generalized Linear Programming Value Function (GVF). It shows the training time, true relative error (a measure of approximation accuracy), and the percentage of constraints satisfied for both models across different instances of the uncapacitated facility location problem (UFL). The results demonstrate the Dual-Stack Model’s effectiveness and competitiveness with a supervised learning method, while highlighting its scalability.

This table compares the performance of the Dual-Stack Model (DSM) and DenseNet in learning the Generalized Linear Programming Value Function (GVF). It shows the training time, true relative error (a measure of approximation accuracy), and the percentage of constraints satisfied during training and testing for both models. The data is broken down by the class of GVF (KG and Euclidean) and the size of the problem instance.

Full paper

#