Statistical Estimation in the Spiked Tensor Model via the Quantum Approximate Optimization Algorithm

↗ OpenReview ↗ NeurIPS Proc. ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial for researchers in quantum computing and statistical inference due to its rigorous analysis of QAOA on a classically challenging problem. It highlights the potential for quantum advantage in statistical estimation, while also providing novel mathematical techniques applicable to other problems. This opens new avenues for investigating quantum algorithms’ performance in computationally hard statistical tasks and comparing them to classical counterparts.

Visual Insights

#

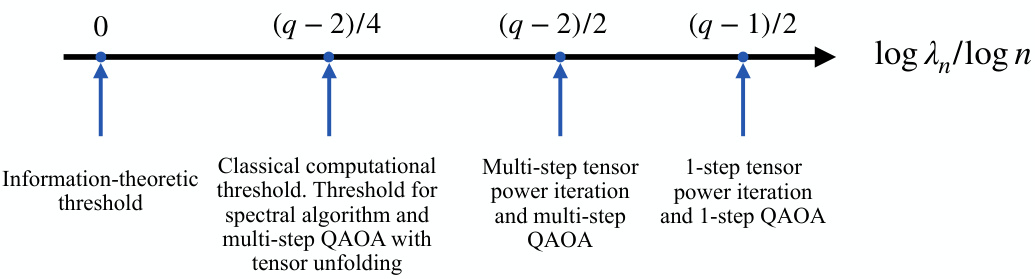
This figure illustrates the different signal-to-noise ratio (SNR) thresholds required for various algorithms to achieve weak recovery in the spiked tensor model. The x-axis represents the log of the SNR scaled by the log of the problem size (n). The y-axis implicitly shows the scaling of the SNR with problem size n. The figure shows that the information-theoretic threshold is constant with n; the classical computational threshold is Θ(n(q-2)/4); the multi-step tensor power iteration and multi-step QAOA thresholds are Θ(n(q-2)/2); and the 1-step tensor power iteration and 1-step QAOA thresholds are Θ(n(q-1)/2).

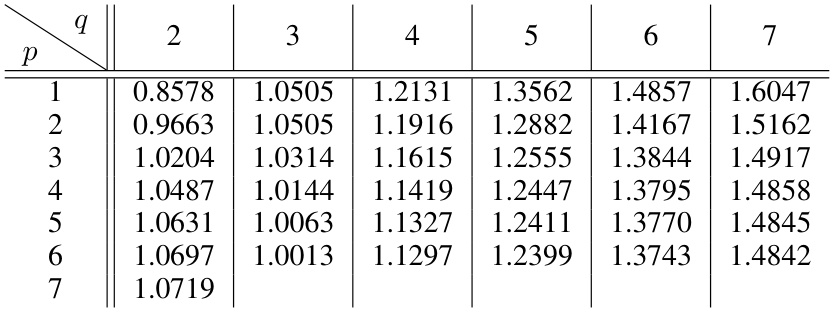
This table presents the quantum enhancement factor achieved by the p-step QAOA over the p-step tensor power iteration for spiked q-tensors in the low signal-to-noise ratio regime. The enhancement factor represents how much the signal-to-noise ratio can be reduced while maintaining the same overlap as classical power iteration. For p=1, the optimal enhancement factor is known and presented in the first row. For p>1, the values shown are numerically optimized and should be considered lower bounds on the true optimal enhancement factors.

In-depth insights

#

QAOA Weak Recovery

#

The study of “QAOA Weak Recovery” explores the capabilities of the Quantum Approximate Optimization Algorithm (QAOA) in addressing the challenge of weak recovery in the spiked tensor model. A key focus is determining the algorithm’s threshold for successful signal recovery, comparing its performance against classical approaches. The analysis delves into the asymptotic behavior of QAOA, characterizing the overlap distribution between the QAOA estimator and the true signal. This leads to the discovery of an intriguing sine-Gaussian law, which contrasts with the behavior of classical methods. Moreover, the research investigates the impact of increasing the number of QAOA steps (depth) on the recovery threshold, aiming to identify potential computational advantages over classical algorithms. The study demonstrates that the QAOA, while possessing interesting properties, does not surpass classical computational thresholds in the constant-depth regime, prompting further investigation into the potential for quantum advantage with larger QAOA depths.

Spiked Tensor QAOA

#

The study of “Spiked Tensor QAOA” blends statistical estimation theory with quantum computing. It investigates the performance of the Quantum Approximate Optimization Algorithm (QAOA) on the spiked tensor model, a problem known for its computational-statistical gap. The research likely focuses on determining if QAOA offers a computational advantage over classical algorithms by analyzing its ability to recover the hidden signal (weak recovery) in the spiked tensor. Key aspects of this analysis likely include determining the algorithm’s recovery threshold (the minimum SNR for successful signal recovery) and characterizing the overlap distribution, comparing it with classical approaches like tensor power iteration. The results may reveal whether QAOA provides a quantum speedup in this specific problem and if so, under what conditions, potentially uncovering new insights into the power of quantum algorithms for classically difficult statistical problems. The research might also explore the impact of QAOA depth and other parameters on performance. A rigorous analysis would require handling combinatorial sums, which might involve advanced mathematical techniques. Ultimately, this area of research aims to bridge classical and quantum approaches to statistical problems, offering potential advancements in both fields.

Overlap Distribution

#

The analysis of overlap distribution in the context of a research paper focusing on statistical estimation using quantum approximate optimization algorithm (QAOA) is crucial. It provides insights into the algorithm’s performance by quantifying the similarity between the estimated signal and the true signal. The distribution’s characteristics, such as its shape and concentration, reveal information about the algorithm’s ability to recover the signal. A well-concentrated distribution around a high overlap value indicates successful recovery, while a dispersed distribution suggests poor performance. Further investigation may reveal interesting patterns, like the observed sine-Gaussian law, which requires further theoretical exploration to understand its implications on recovery thresholds and computational advantages over classical methods. Comparing overlap distributions obtained from QAOA with those from classical approaches, such as tensor power iteration, helps assess the potential quantum advantage. Deviations from the expected distribution under certain conditions provide valuable insights into the algorithm’s limitations and suggest areas for future improvements. Investigating the overlap’s dependence on various parameters, like the number of steps in QAOA and the signal-to-noise ratio, can offer more comprehensive understanding of the algorithm’s behavior and the problem’s inherent computational-statistical gap. The study of the overlap distribution contributes significantly to evaluating the effectiveness of QAOA for statistical estimation problems, particularly those exhibiting large computational-statistical gaps.

Classical Thresholds

#

The concept of “Classical Thresholds” in the context of spiked tensor models refers to the signal-to-noise ratio (SNR) levels beyond which classical algorithms can reliably recover the planted signal. These thresholds represent a fundamental limit in the computational complexity of the problem, highlighting a computational-statistical gap. Below the threshold, the problem is computationally intractable for classical algorithms, despite being information-theoretically solvable. Above the threshold, efficient algorithms exist that can successfully recover the signal. Understanding these thresholds is crucial for benchmarking the performance of both classical and quantum algorithms. The significant gap between the information-theoretic threshold (where recovery is theoretically possible) and the classical computational threshold underscores the difficulty of the problem for classical approaches, motivating the exploration of alternative methods like quantum algorithms.

Future QAOA Research

#

Future research directions for the Quantum Approximate Optimization Algorithm (QAOA) are multifaceted. Improving the theoretical understanding of QAOA’s performance beyond shallow depths is crucial, as current analyses often struggle to handle the complexity of deeper circuits. This necessitates developing novel analytical techniques to accurately predict QAOA’s behavior in solving complex optimization problems. Exploring adaptive and hybrid QAOA approaches that dynamically adjust parameters or combine QAOA with classical methods may significantly enhance its performance and efficiency. Developing techniques to mitigate the effects of noise and decoherence inherent in near-term quantum devices is vital for practical applications. Finally, investigating QAOA’s potential for quantum advantage in specific problem domains, particularly those exhibiting a large computational-statistical gap, is key to demonstrating its practical utility and furthering the field of quantum computing.

More visual insights

#

More on figures

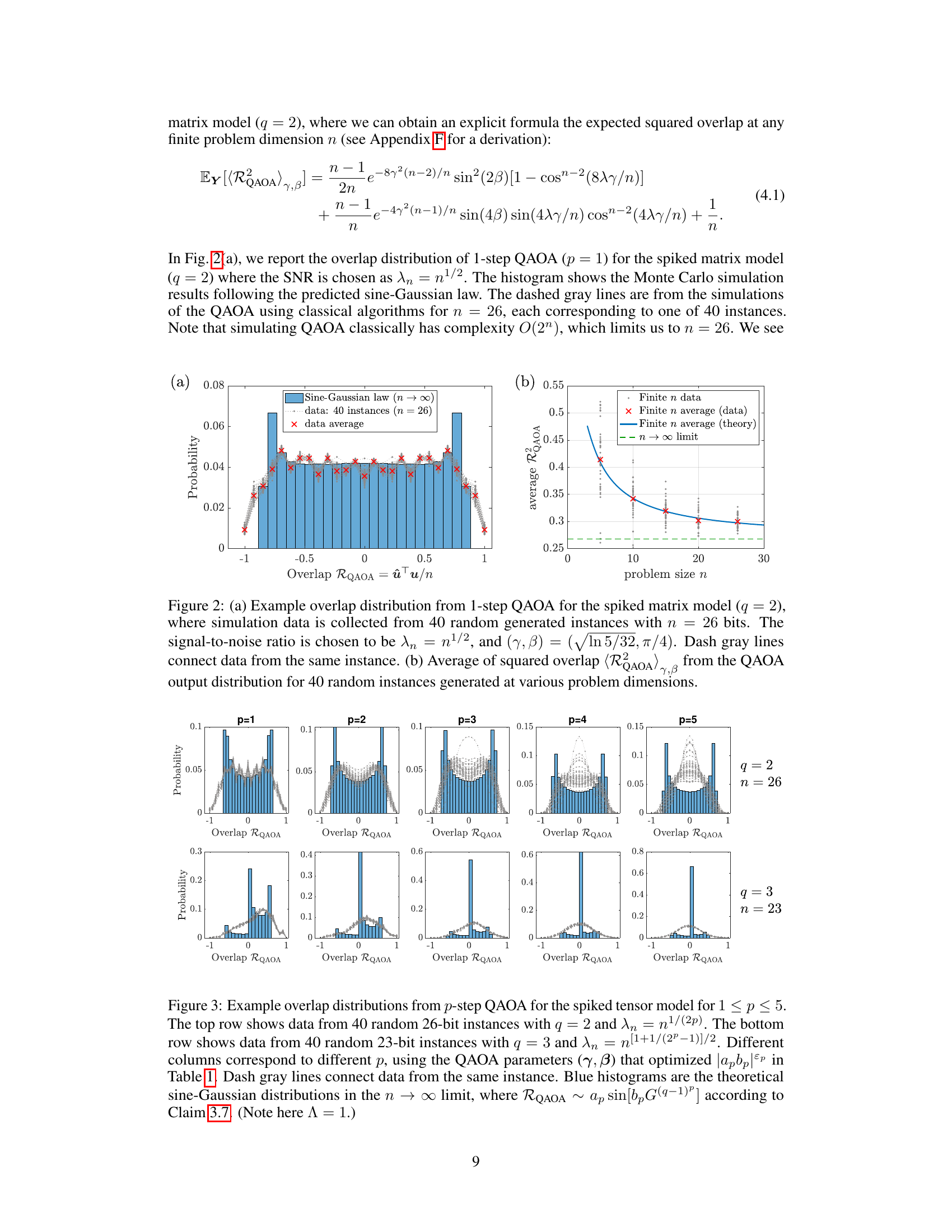
Figure 2(a) shows the overlap distribution obtained from numerical simulations of the 1-step QAOA on the spiked matrix model (q=2) with n=26 qubits. The signal-to-noise ratio is set to λn = n1/2 and parameters (γ, β) = (ln 5/32, π/4). The histogram displays the Monte Carlo simulation results, which are compared to the theoretical sine-Gaussian law. The dashed gray lines connect data points from the same instance. Figure 2(b) displays the average squared overlap from the QAOA output distribution over 40 random instances at various problem sizes (n). The results show that the average squared overlap converges to the theoretical value in the n→∞ limit, with deviations consistent with the rigorous finite-n calculation reported in Equation (4.1).

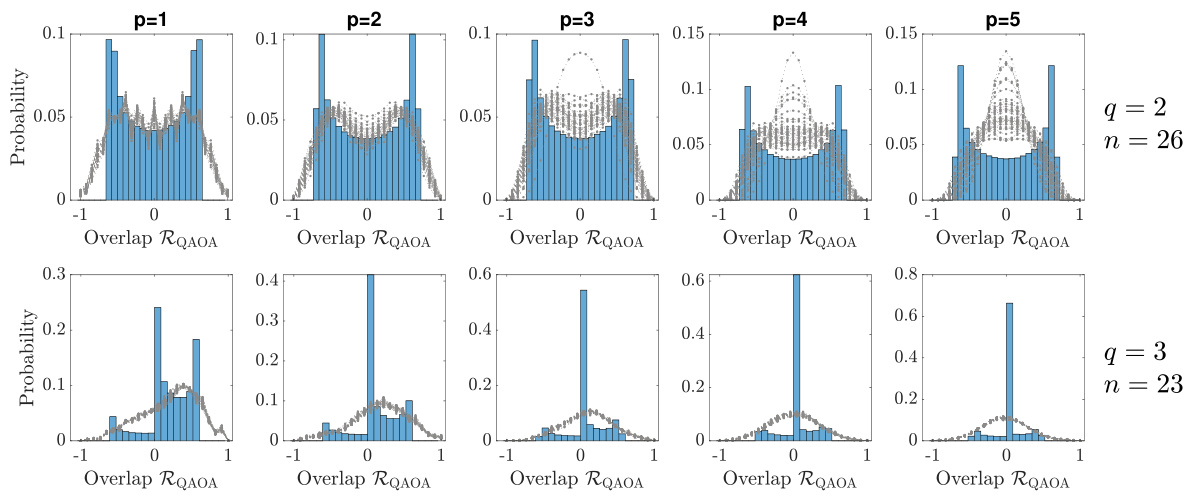
The figure shows the overlap distributions obtained from numerical simulations of the p-step QAOA algorithm for different values of p (number of steps) and q (tensor order). The top half displays results for q=2 and the bottom half for q=3. Each subplot represents a different value of p and shows the overlap distribution for 40 independent runs, highlighting the algorithm’s performance in terms of overlap with the planted signal. Blue histograms represent the theoretical sine-Gaussian distribution. Gray lines connect data from the same instance.

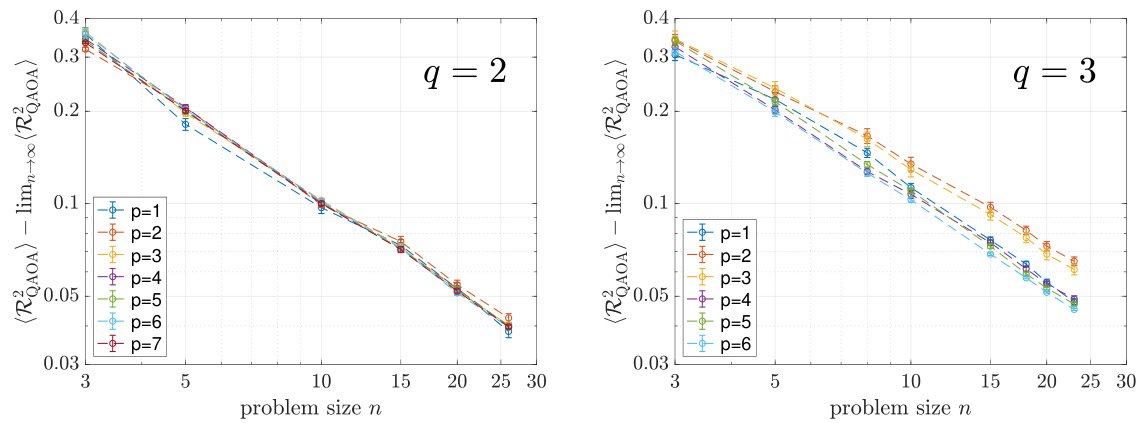
This figure displays the second moment of QAOA overlap versus the problem size n for various QAOA depths p and tensor orders q. The y-axis represents the difference between the simulated second moment of the overlap and the theoretical value predicted by the sine-Gaussian law in the limit of large n. The plots show that the simulations appear to converge to the theoretical value with deviations of order 1/n. This observation is consistent with the rigorously derived finite-n formula for the case (p, q) = (1, 2).

Full paper

#