Enhancing Robustness of Graph Neural Networks on Social Media with Explainable Inverse Reinforcement Learning

↗ OpenReview ↗ NeurIPS Proc. ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial because it tackles the critical issue of enhancing the robustness of graph neural networks (GNNs) against adversarial attacks, a prevalent problem in social media analysis. The proposed method, MoE-BiEntIRL, offers a novel and effective approach that is both interpretable and efficient, paving the way for more secure and reliable GNN applications. This addresses a significant gap in current research, enhancing GNNs’ real-world applicability and inspiring new research directions in adversarial defense strategies.

Visual Insights

#

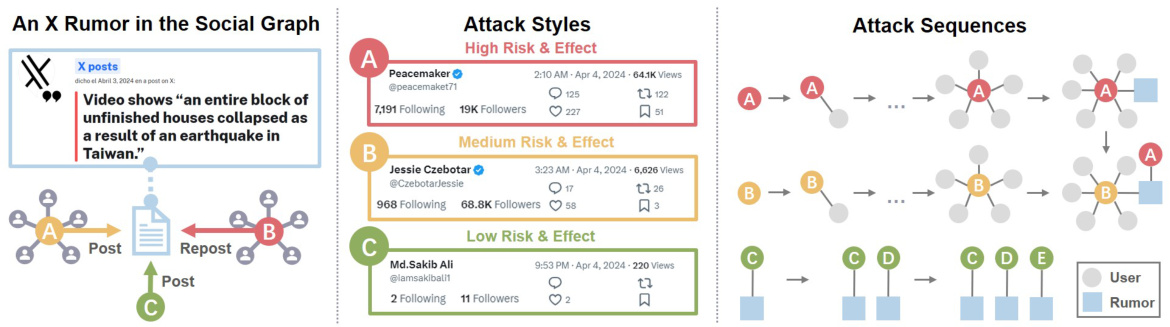
This figure showcases three different attack scenarios on a social media platform (X, formerly Twitter). Each scenario shows how a rumor spreads through different methods and with varying degrees of success, highlighting the diverse attack styles and sequences used by malicious actors to manipulate information spread.

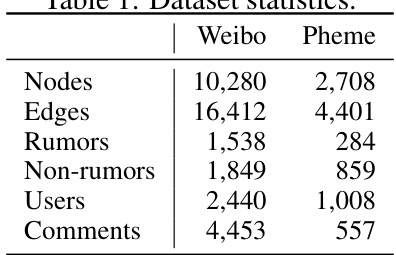
This table presents the key statistics for the two datasets used in the paper’s experiments: Weibo and Pheme. For each dataset, it shows the number of nodes (representing messages, users, and comments), edges (relationships between nodes), rumors, non-rumors, unique users, and comments.

In-depth insights

#

Adversarial GNNs

#

Adversarial attacks on Graph Neural Networks (GNNs) represent a significant challenge, as even small, carefully crafted perturbations to the graph structure can drastically alter GNN predictions. These attacks exploit the inherent vulnerabilities of GNNs to subtle changes in their input data, which are often difficult to detect and mitigate. The research into adversarial GNNs focuses on understanding the mechanisms behind these attacks, developing robust defense strategies, and designing GNN architectures that are inherently more resilient. Defense methods range from adversarial training, which involves exposing the GNN to adversarial examples during training, to using more robust graph representations that are less susceptible to manipulation. However, the development of effective defenses against increasingly sophisticated adversarial attacks remains an active area of research. Another crucial aspect is the explainability of adversarial attacks and defenses. Understanding why a particular attack is successful or a particular defense fails is key to improving both the efficacy of attacks and the robustness of defenses. Ultimately, robust and explainable GNNs are critical for trustworthy deployment in security-sensitive applications.

MoE-BiEntIRL

#

MoE-BiEntIRL, a name suggestive of a novel approach to inverse reinforcement learning (IRL), likely combines Mixture of Experts (MoE) with a Bidirectional update mechanism within a Maximum Entropy IRL framework. MoE enhances the model’s capacity to handle diverse attack strategies seen in social networks by allowing different experts to specialize in various attack styles. Bidirectional updates likely refine both the policy and reward function simultaneously, improving accuracy and efficiency. The maximum entropy aspect suggests a focus on robustness and generalization, making the approach less susceptible to overfitting. The overall goal is likely to reconstruct attacker policies from observed attack trajectories for improved defense of graph neural networks, which is a significant contribution towards making social media platforms more secure. Explainability may be incorporated by utilizing interpretable reward functions, providing valuable insights into attacker behaviour.

Policy Recovery

#

Policy recovery, in the context of adversarial attacks on graph neural networks (GNNs), focuses on reconstructing the attack strategies employed by malicious actors. This is crucial for enhancing GNN robustness. By analyzing captured attack trajectories, a model can learn the underlying reward function guiding the attacker’s behavior. Maximum entropy inverse reinforcement learning (IRL) is a promising technique for this, enabling the model to infer the reward function and thus the attacker’s policy from observed actions. However, real-world attacks are diverse and complex. Therefore, a key challenge lies in handling multi-source attacks from adversaries with varying motives and capabilities. Mixture-of-experts (MoE) models can address this by combining multiple expert policies to represent the wide range of attack styles. This helps in generating more diverse and effective adversarial samples for defense. Furthermore, the learned policy must also be interpretable so that the underlying attack behaviors can be better understood. This understanding can inform the development of targeted defenses, while also helping to profile attackers and improve overall security.

Robustness Gains

#

The concept of “Robustness Gains” in the context of a research paper likely refers to improvements in the stability and reliability of a model or system, especially in the face of adversarial attacks or noisy data. A thoughtful analysis would delve into how these gains were achieved. Were they the result of improved model architectures, novel training techniques (such as adversarial training), enhanced data augmentation strategies, or a combination thereof? Quantifying these gains is crucial, and the paper should present metrics to demonstrate the improvements. Key metrics might include accuracy under attack, error rates on noisy data, or resilience scores which would help to understand the robustness increase. Additionally, the analysis must address the scope of the gains. Do the improvements apply broadly across various attack types and data conditions, or are they limited to specific scenarios? Finally, the paper should ideally offer insights into why these robustness gains were achieved, providing a mechanistic understanding rather than just reporting the results. This might involve discussions on how the proposed methods address the vulnerabilities of existing approaches, leading to a more robust system. The overall value of the “Robustness Gains” section would depend on the thoroughness of the evaluation, the clarity of the presentation, and the depth of the analysis, providing a convincing argument for the significance of the work.

Interpretability

#

The concept of interpretability is crucial in the context of this research paper, especially when dealing with the complex nature of graph neural networks (GNNs) applied to social media analysis. The authors emphasize the importance of explainable inverse reinforcement learning (IRL). The aim is not only to enhance the robustness of GNNs against adversarial attacks but also to gain a deeper understanding of the attacks themselves. By employing methods that produce feature-level explanations, the researchers attempt to make the decision-making process of the models more transparent and understandable. This approach is highly valuable as it offers insights into the attackers’ strategies and helps in developing more effective defense mechanisms. The use of interpretable linear reward functions further aids in this endeavor by providing clear, concise explanations of the attack behaviors. Ultimately, the pursuit of interpretability in this research goes beyond mere technical enhancement; it is a fundamental step towards building trust and accountability in the application of GNNs for critical tasks like rumor detection on social media platforms.

More visual insights

#

More on figures

This figure illustrates the three-stage framework of the proposed MoE-BiEntIRL method: attack, reconstruction, and defense. The attack stage shows multiple attackers generating various attack trajectories on a social network graph. The reconstruction stage uses a mixture-of-experts (MoE) model and maximum entropy inverse reinforcement learning (EntIRL) to learn the attack policy from the observed trajectories, leveraging precise sample guidance and a bidirectional update mechanism to improve accuracy. The defense stage utilizes the reconstructed attack policy to generate additional adversarial samples, which are then used for data augmentation and adversarial training of a targeted model, enhancing its robustness against attacks. The top-right corner shows an example of an attack trajectory involving subgraph selection and node manipulation. The figure provides a comprehensive overview of the proposed methodology for improving the robustness of graph neural networks (GNNs) in social media analysis.

This figure illustrates the proposed MoE-BiEntIRL framework which consists of three main stages: attack, reconstruction, and defense. The ‘attack’ stage shows various attackers manipulating the social network graph using different attack methods. The ‘reconstruction’ stage uses the MoE-BiEntIRL method (mixture-of-experts bidirectional update maximum entropy inverse reinforcement learning) to learn the attack policy from collected attack trajectories. This stage incorporates precise sample guidance and a bidirectional update mechanism to improve the accuracy and efficiency of policy reconstruction. Finally, the ‘defense’ stage uses the learned attack policy to generate additional adversarial samples to enhance the robustness of the target GNN model through data augmentation and adversarial training. An example of a specific attack trajectory in a social network is provided in the top right corner.

More on tables

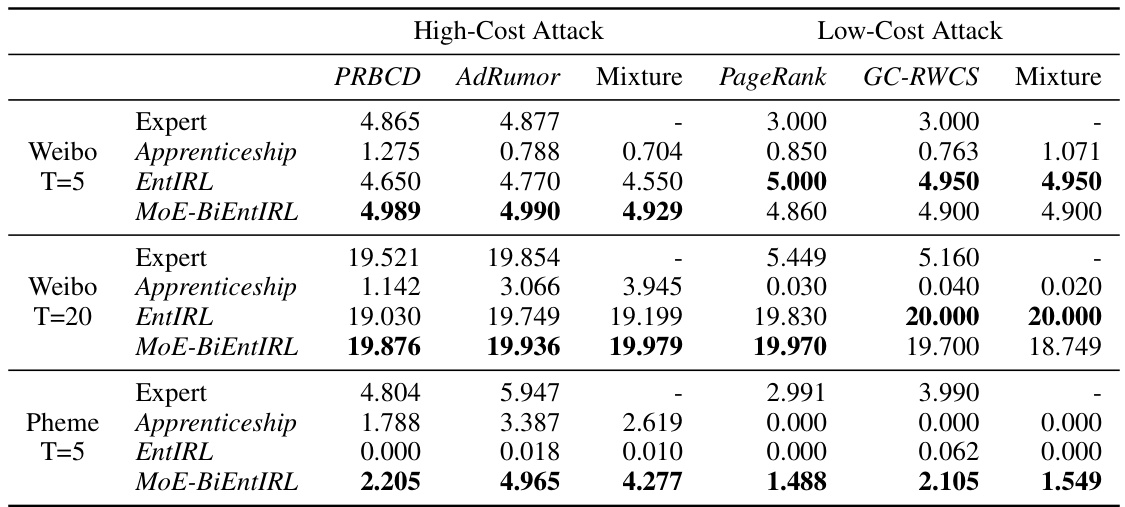
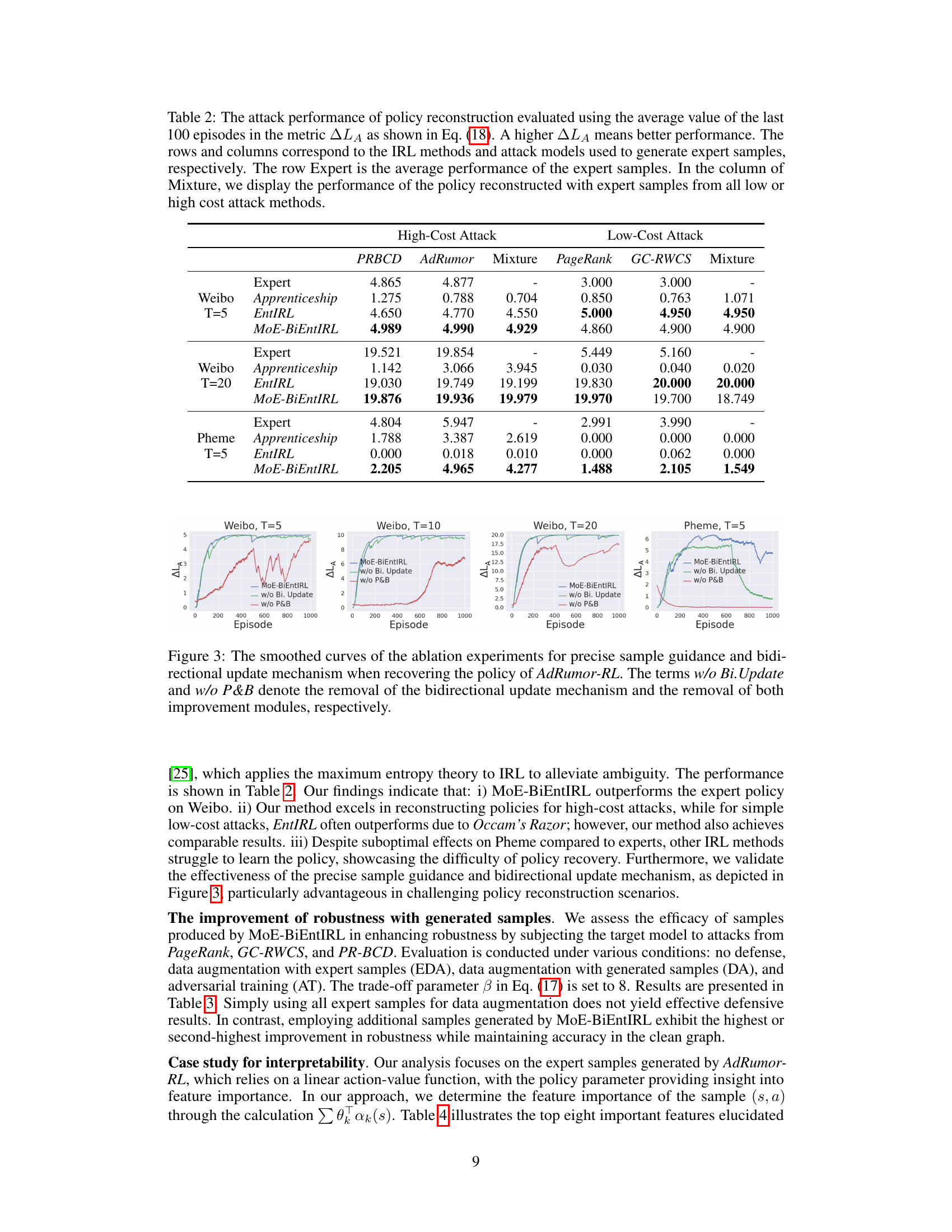
This table presents the performance comparison of different inverse reinforcement learning (IRL) methods in reconstructing attack policies. The performance is measured by the average attack loss (∆LA) over the last 100 episodes of the reconstruction process. It compares three IRL methods (Apprenticeship, EntIRL, MoE-BiEntIRL) against four attack methods (PRBCD, AdRumor, PageRank, GC-RWCS) at different attack budgets (T=5, T=20) and on different datasets (Weibo, Pheme). A higher ∆LA indicates better performance in approximating the original attack policy.

This table presents the performance of three different inverse reinforcement learning (IRL) methods in reconstructing attack policies. It compares the performance of Apprenticeship Learning, EntIRL, and the proposed MoE-BiEntIRL on four different types of graph adversarial attacks (PR-BCD, AdRumor-RL, PageRank, GC-RWCS). The performance is measured using the average ∆LA (attack loss difference) over the last 100 episodes of training for each method and attack type, with higher values representing better performance. A mixture of low and high cost attack samples is also tested for each method.

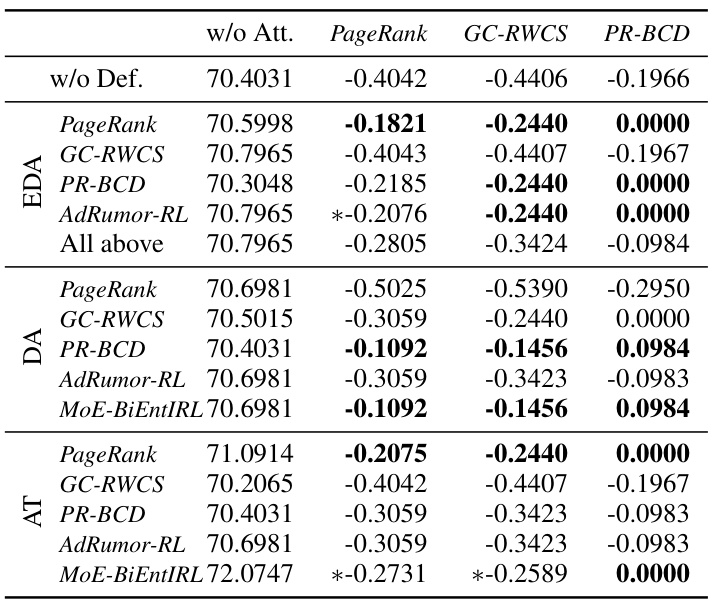
This table shows the test accuracy decline of a GCN rumor detector on the Weibo dataset after applying different defense methods against various graph adversarial attacks (PageRank, GC-RWCS, PR-BCD, AdRumor-RL). It compares the accuracy decline without any defense (w/o Def), with data augmentation using expert samples (EDA), data augmentation using samples generated by MoE-BiEntIRL (DA), and adversarial training (AT). The best and second-best performing methods are highlighted.

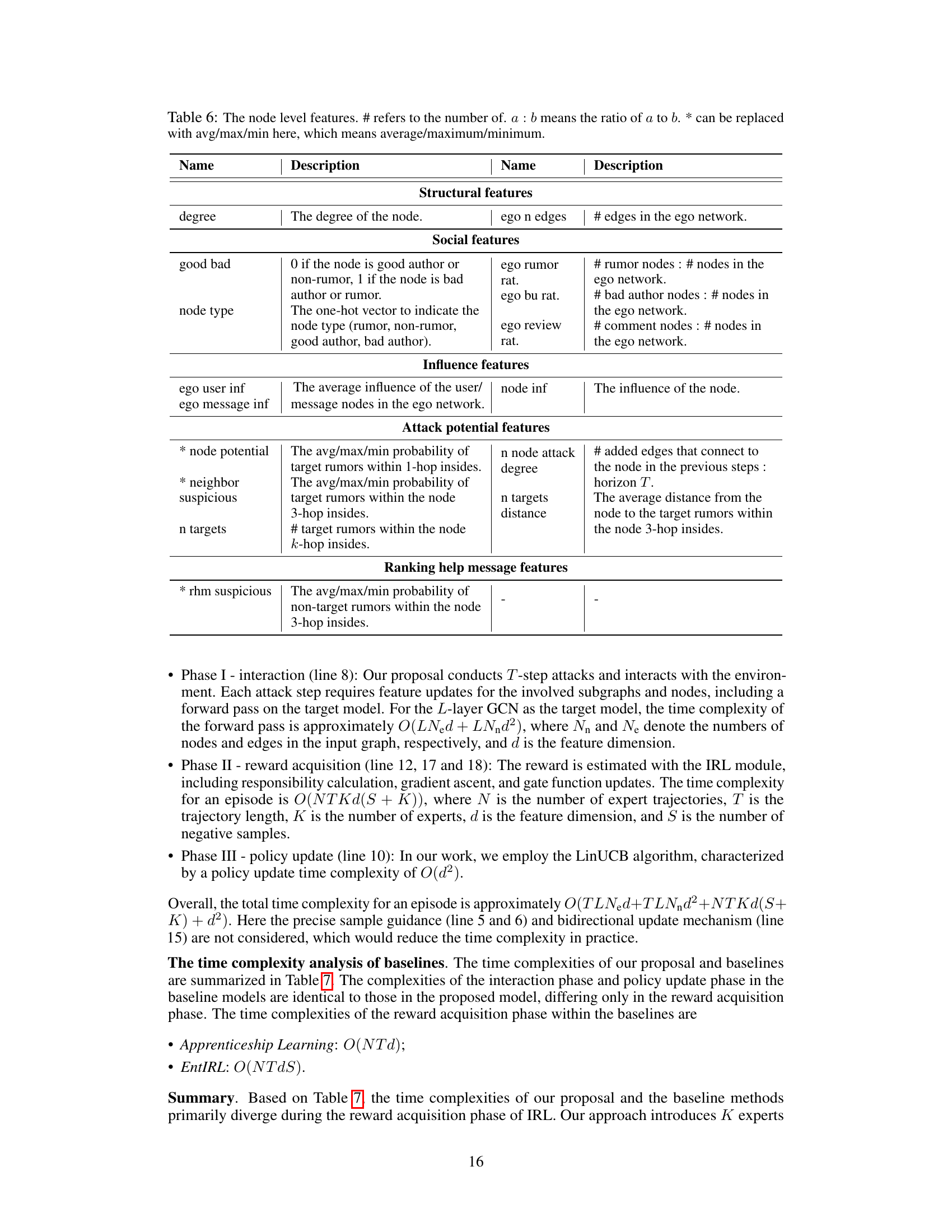
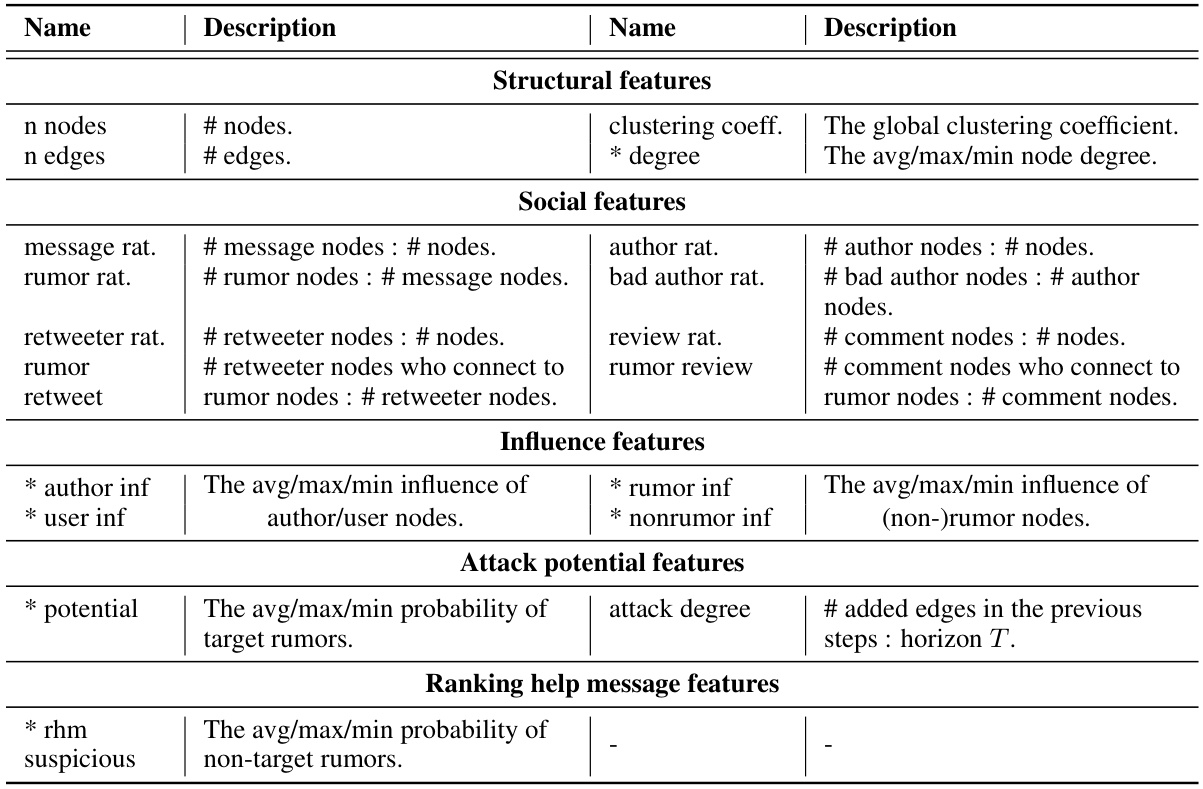
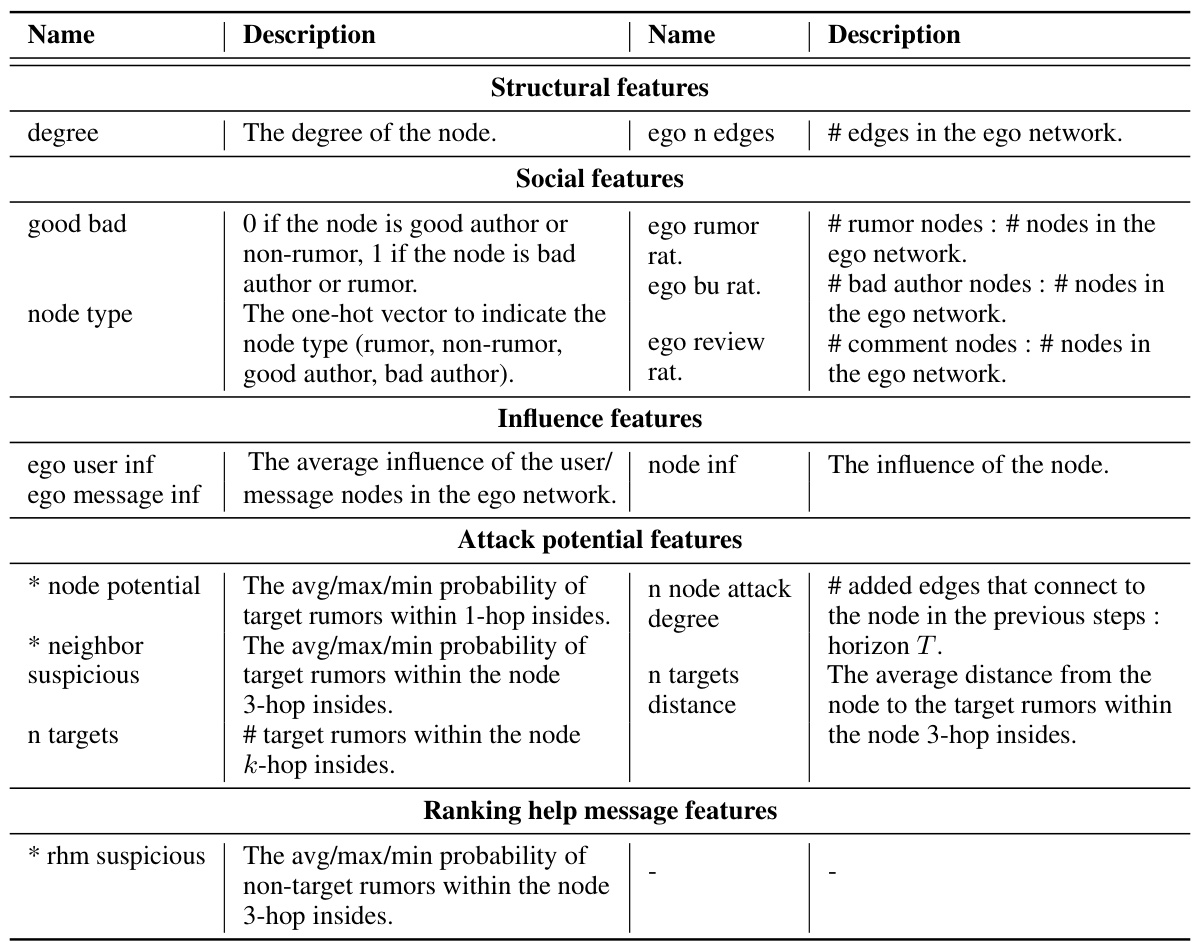
This table shows the top 8 most important features for subgraph selection in the Adversarial Rumor-RL attack model, as determined by both expert samples and the learned reward function. Features are categorized into ‘Source Subgraph’, ‘Destination Subgraph’, and a few additional features. Overlapping features between the expert sample analysis and the reward function are highlighted with a gray background. More details on the features themselves are available in Appendix C of the paper.

This table presents the test accuracy decline of a Graph Convolutional Network (GCN) rumor detector on the Weibo dataset under different attack scenarios. It shows the impact of using adversarial samples generated by various methods to improve robustness, along with comparison to the results without using adversarial training and data augmentation.

This table presents the test accuracy decline of a GCN rumor detector on the Weibo dataset with different defense methods against various attack strategies. The results show the accuracy decline when no defense is applied and when various robustness enhancement techniques are used. The table also highlights the best-performing method(s) for each attack type.

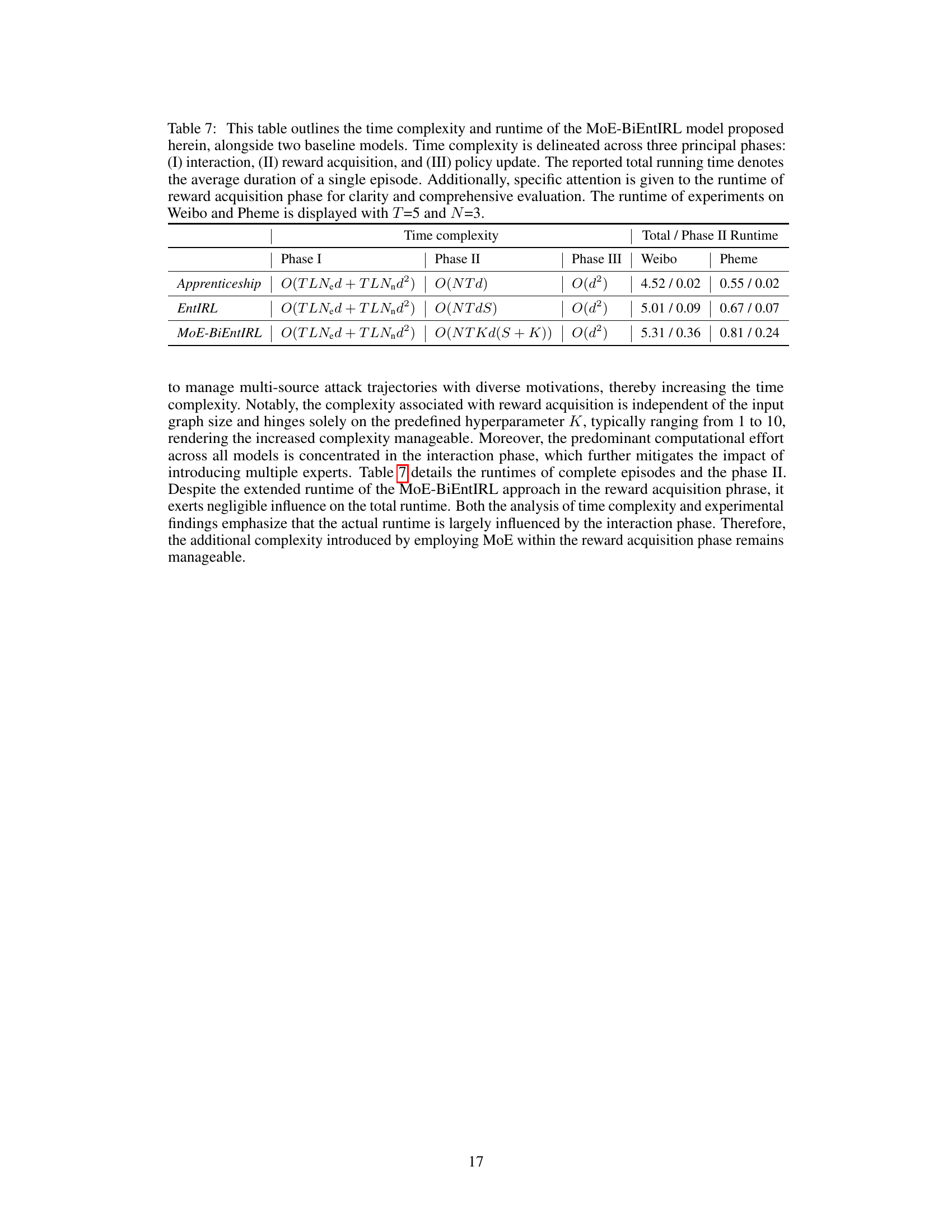
This table compares the time complexity and runtime of three models: MoE-BiEntIRL, Apprenticeship, and EntIRL. The comparison is broken down into three phases: interaction, reward acquisition, and policy update. The table shows the time complexity for each phase and the total runtime for experiments performed on Weibo and Pheme datasets with specific parameter values (T=5 and N=3).

Full paper

#