↗ OpenReview ↗ NeurIPS Proc. ↗ Hugging Face ↗ Chat
TL;DR#
Large Language Models (LLMs) are memory-bound, hindering their deployment. Post-training quantization (PTQ) aims to reduce memory footprint by quantizing weights to lower precision, but existing methods like vector quantization are limited by codebook size. This restricts them to low dimensions, limiting quantization quality.
QTIP uses trellis-coded quantization (TCQ) to overcome this. TCQ separates codebook size from dimensionality, allowing for ultra-high-dimensional quantization. QTIP designs hardware-efficient codes for a ‘bitshift’ trellis structure, enabling parallel decoding and avoiding large codebook storage. The results show that QTIP achieves state-of-the-art performance in both quantization quality and inference speed, significantly outperforming existing methods.
Key Takeaways#
Why does it matter?#
This paper is important because it presents QTIP, a novel quantization technique that achieves state-of-the-art results in both quantization quality and inference speed for LLMs. This addresses a critical challenge in deploying large language models, paving the way for more efficient and accessible AI applications. The introduction of novel, hardware-efficient codes for trellis-coded quantization opens exciting new avenues for research in model compression and efficient inference.
Visual Insights#
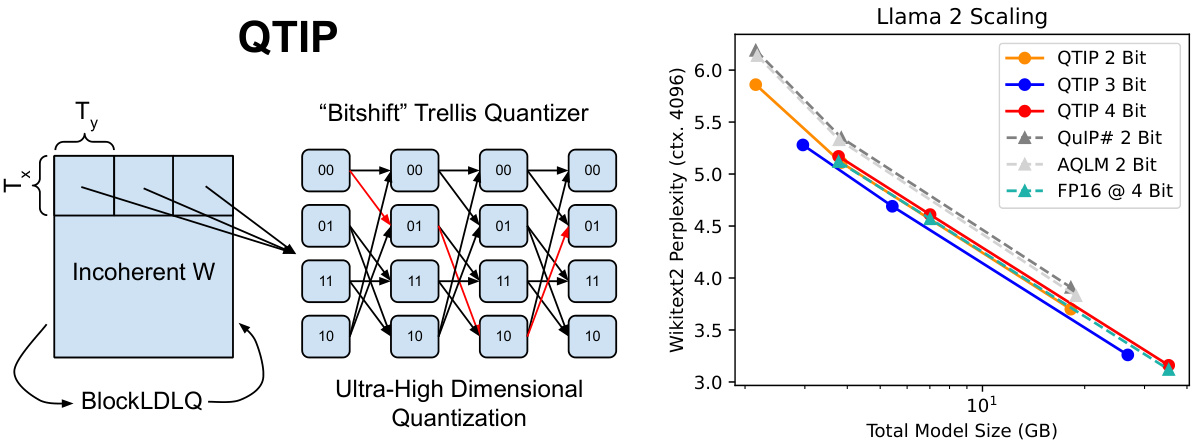
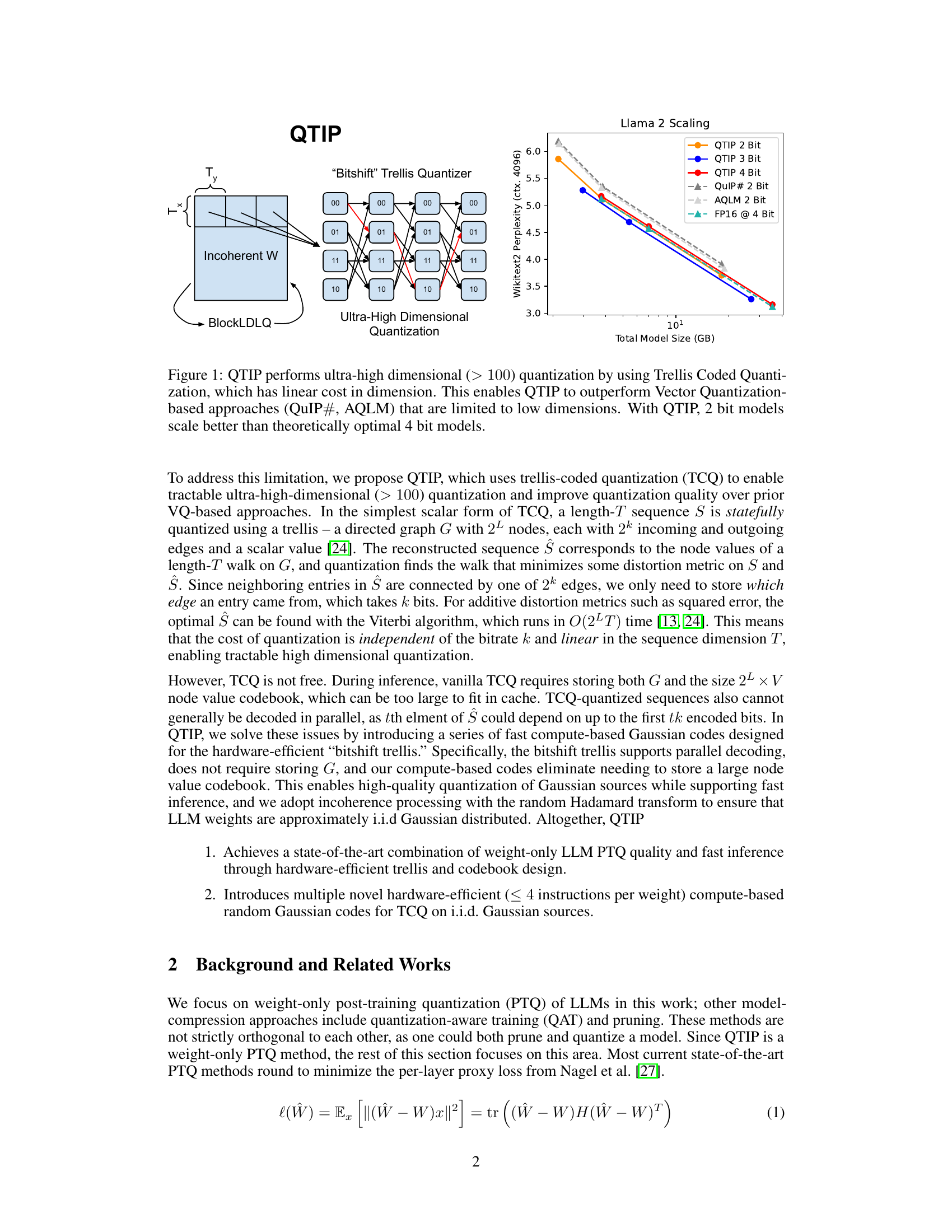
This figure demonstrates QTIP’s ability to perform ultra-high dimensional quantization using Trellis Coded Quantization (TCQ). The left side shows a diagram of the QTIP architecture, highlighting the use of an incoherent weight matrix and a ‘bitshift’ trellis quantizer to achieve this. The right side presents a graph showing the Wikitext-2 perplexity of Llama 2 models quantized using different methods (QTIP with varying bit depths, QuIP#, AQLM, and FP16) as a function of model size. This graph highlights QTIP’s superior performance in achieving better perplexity (lower is better) with lower bit depths compared to other quantization techniques, especially as the model size grows. The graph shows that 2-bit QTIP models perform better than theoretically optimal 4-bit models, demonstrating the effectiveness of the ultra-high dimensional approach.

This table compares the mean squared error (MSE) achieved by different quantization techniques when applied to an independent and identically distributed (i.i.d.) Gaussian source. The techniques include scalar quantization (SQ), vector quantization (VQ), and various trellis coded quantization (TCQ) methods. The table shows that high-dimensional TCQ methods using compute-based codes achieve MSE values close to the theoretical lower bound, significantly outperforming SQ and VQ.
In-depth insights#
Trellis Coded Quant#
Trellis coded quantization (TCQ) offers a compelling alternative to traditional vector quantization (VQ) for post-training quantization (PTQ) of large language models (LLMs). TCQ’s key advantage lies in its ability to handle ultra-high dimensional quantization with linear complexity, unlike VQ’s exponential scaling. This allows for significantly improved quantization quality by leveraging more nuanced codebook shaping. However, TCQ’s stateful decoder presents challenges for efficient inference, potentially requiring significant memory and computation. The solution explored uses a stateful decoder that separates codebook size from bitrate and effective dimension. Furthermore, the use of fast compute-based Gaussian codes designed for a hardware-efficient ‘bitshift’ trellis structure allows for parallel decoding and the elimination of codebook storage, resulting in state-of-the-art results in both quantization quality and inference speed. The technique’s effectiveness hinges on the inherent properties of the weights within LLMs after the application of incoherence processing, enabling the approximation of i.i.d. Gaussian distributed weights which are well suited to TCQ. The overall design is presented as a flexible drop-in replacement for existing VQ-based methods, offering a pathway to enhanced LLM compression and improved efficiency across hardware platforms.
High-Dim Quant#
The concept of “High-Dim Quant” likely refers to high-dimensional quantization techniques in the context of large language models (LLMs). This approach tackles the memory limitations of LLMs by quantizing their weights to lower precision, significantly reducing memory footprint and improving inference speed. The “High-Dim” aspect is crucial as it suggests quantizing multiple weights simultaneously, leveraging the statistical properties of weight vectors to achieve better information compression. Traditional methods often rely on scalar quantization, limiting compression capabilities. High-dimensional quantization, in contrast, is expected to offer superior compression and better quantization quality, while posing computational challenges. This approach likely involves advanced methods such as vector quantization or trellis-coded quantization to handle the complexity of high-dimensional spaces effectively. The trade-off between computational cost and compression gain is a key challenge, and effective algorithms and hardware support are essential for practical implementation. The research likely explores novel algorithms to efficiently achieve this, perhaps incorporating hardware-friendly techniques like the “bitshift trellis” to improve decoding speeds during inference.
Incoherence Proc#
Incoherence processing, a crucial technique in post-training quantization (PTQ) for large language models (LLMs), aims to improve quantization quality by manipulating the weight matrix. The core idea is to transform the weight matrix into a state where its entries are approximately independent and identically distributed (i.i.d.), resembling a Gaussian distribution. This transformation, often achieved using random orthogonal matrices such as the random Hadamard transform, reduces the impact of outliers and correlations among weights. This i.i.d. property is beneficial because many quantization techniques, particularly those involving trellises, perform optimally or near-optimally under i.i.d. assumptions. While incoherence processing adds computational overhead, it significantly enhances quantization quality, leading to improved compression ratios and faster inference speeds without substantial accuracy loss. The effectiveness of incoherence processing hinges on the appropriateness of the chosen transformation and its compatibility with the subsequent quantization method. Thus, careful consideration of both the transformation and quantization technique is needed to optimize the overall PTQ workflow.
Fast Inference#
Fast inference is a critical aspect of large language models (LLMs), especially for real-time applications. The paper explores this extensively by focusing on post-training quantization (PTQ) techniques to reduce the memory footprint and computational cost of LLMs. High-dimensional quantization is highlighted as key to achieving both high quality and speed. Traditional vector quantization methods suffer from computational complexity that scales exponentially with dimensionality. The paper introduces trellis-coded quantization (TCQ) as a solution, which offers linear complexity, enabling ultra-high-dimensional quantization. However, standard TCQ requires substantial storage for the trellis and codebook, hindering fast inference. To address this, the authors present QTIP, which uses a novel bitshift trellis structure, enabling parallel decoding and reducing storage needs. They also introduce compute-based codes, which eliminate the need to store large codebooks entirely. These optimizations are crucial for hardware-efficient inference and improved performance. The effectiveness of these approaches is demonstrated through comparisons to existing state-of-the-art methods, showcasing that QTIP achieves superior performance across various metrics.
LLM Compression#
LLM compression techniques are crucial for deploying large language models (LLMs) efficiently. Post-training quantization (PTQ), a prominent method, reduces memory footprint and improves inference speed by representing weights with lower precision datatypes. While methods like vector quantization (VQ) offer improved information utilization, they are limited by their exponential complexity. Trellis-coded quantization (TCQ) provides a promising alternative, enabling ultra-high-dimensional quantization with linear complexity. Incoherence processing, coupled with TCQ, further enhances compression by transforming LLM weights into a more suitable distribution for quantization. The choice between lookup-based and compute-based TCQ methods involves a tradeoff between speed and memory requirements. Hardware-efficient trellis structures, such as the bitshift trellis, are vital for achieving fast inference speeds. Overall, LLM compression is an active research area with ongoing efforts to balance compression ratio, computational cost, and accuracy.
More visual insights#
More on figures
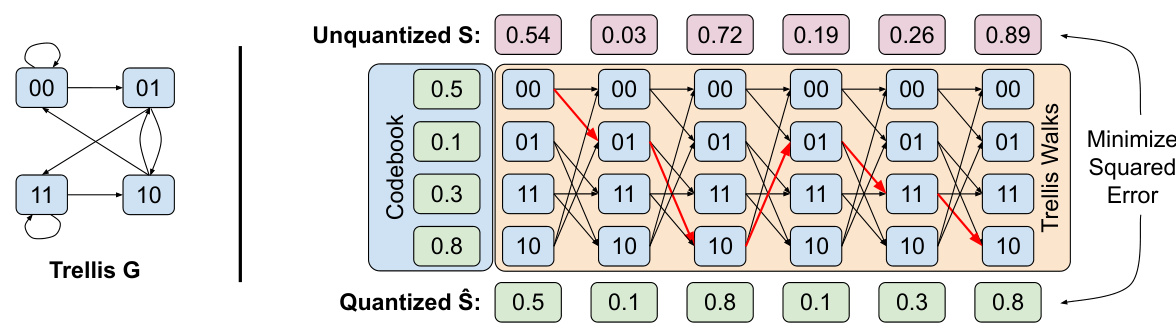
This figure illustrates a simple bitshift trellis with parameters L=2, k=1, V=1. It shows how nodes are connected based on overlapping bits, enabling parallel decoding and efficient storage. The example demonstrates how a sequence is quantized using trellis walks, minimizing squared error.
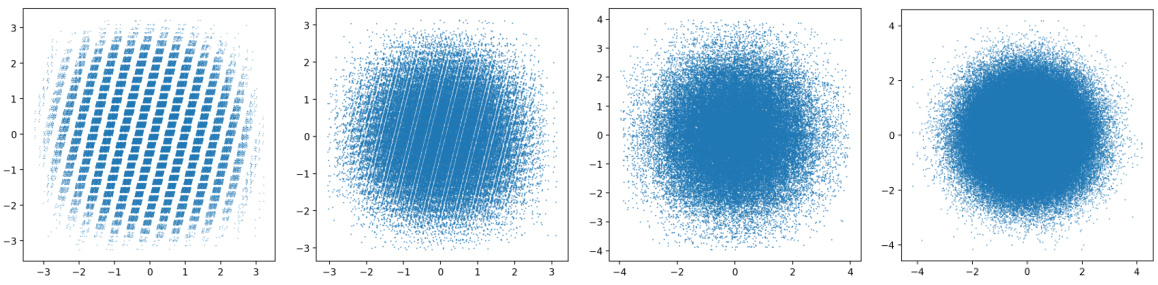
This figure compares the distribution of quantized values produced by different methods in a bitshift trellis. It shows that while a naive approach leads to strong correlations, the proposed algorithms (1MAD and 3INST) generate values closer to a random Gaussian distribution, thus improving quantization quality.
More on tables

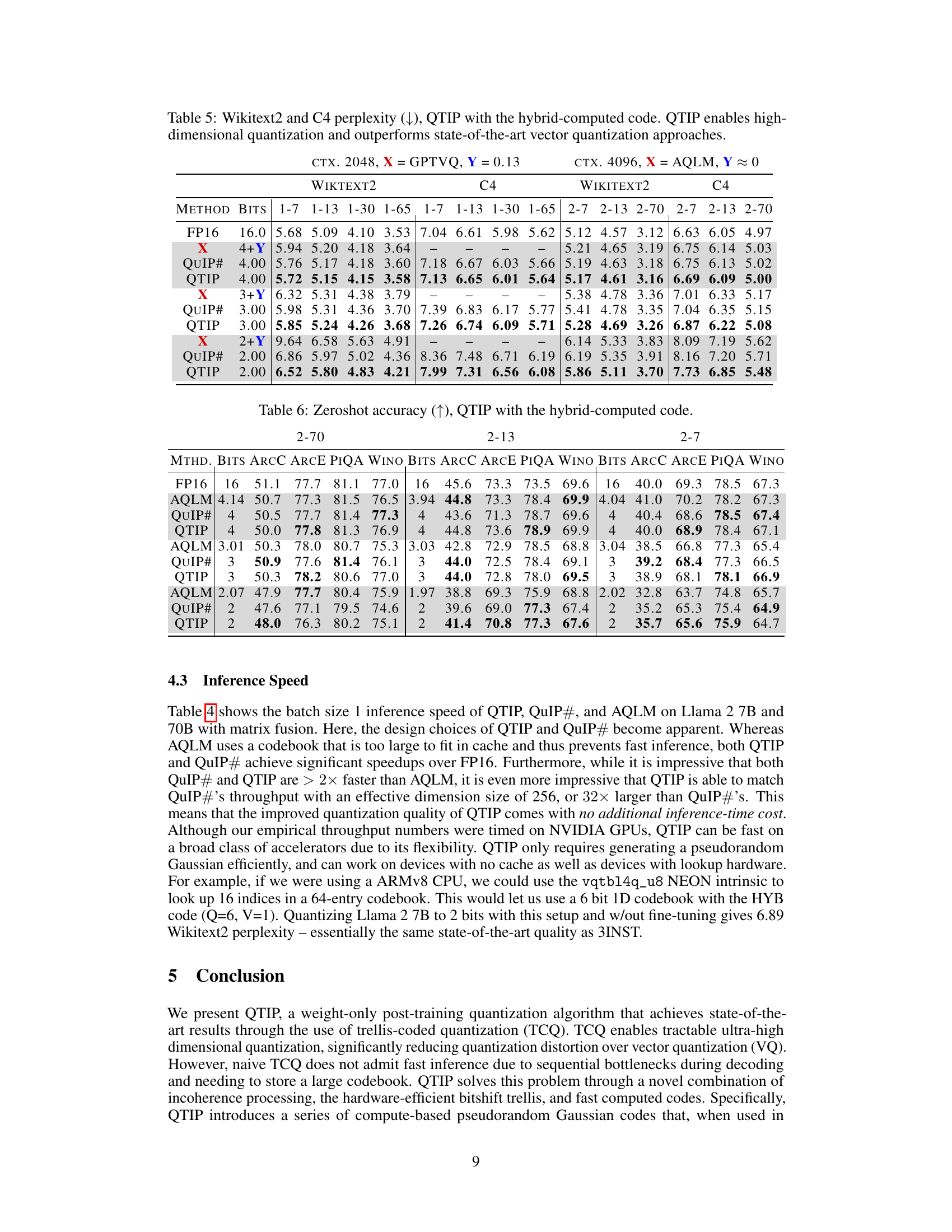
This table presents the results of experiments evaluating the performance of QTIP with pure-computed codes on the Wikitext2 and C4 datasets. The perplexity, a measure of how well a language model predicts a sample, is shown for different model sizes and bit depths (2-bit, 3-bit, and 4-bit). The results highlight that even without the fine-tuning process used in QuIP# and AQLM, QTIP still surpasses the performance of these state-of-the-art methods.

This table presents the results of experiments evaluating the performance of QTIP with pure-computed codes on the Wikitext2 and C4 datasets. It compares the perplexity achieved by QTIP (using 1MAD and 3INST codes) at different bitrates (2-bit, 3-bit, and 4-bit) against the results from QuIP# and AQLM, which are state-of-the-art methods that do employ fine-tuning. The key finding is that QTIP consistently outperforms QuIP# and AQLM even without fine-tuning, highlighting its effectiveness in achieving high-quality quantization.

This table shows the results of experiments conducted using pure-computed codes on Wikitext2 and C4 datasets. The perplexity metric, which measures the model’s ability to predict the next word in a sequence, is used to evaluate the performance of different quantization methods (QTIP, QuIP#, AQLM). The results demonstrate that QTIP, even without fine-tuning, consistently outperforms both QuIP# and AQLM, which utilize fine-tuning. This highlights QTIP’s effectiveness in achieving superior quantization quality.
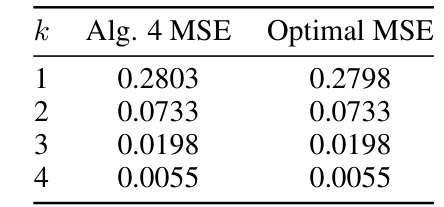
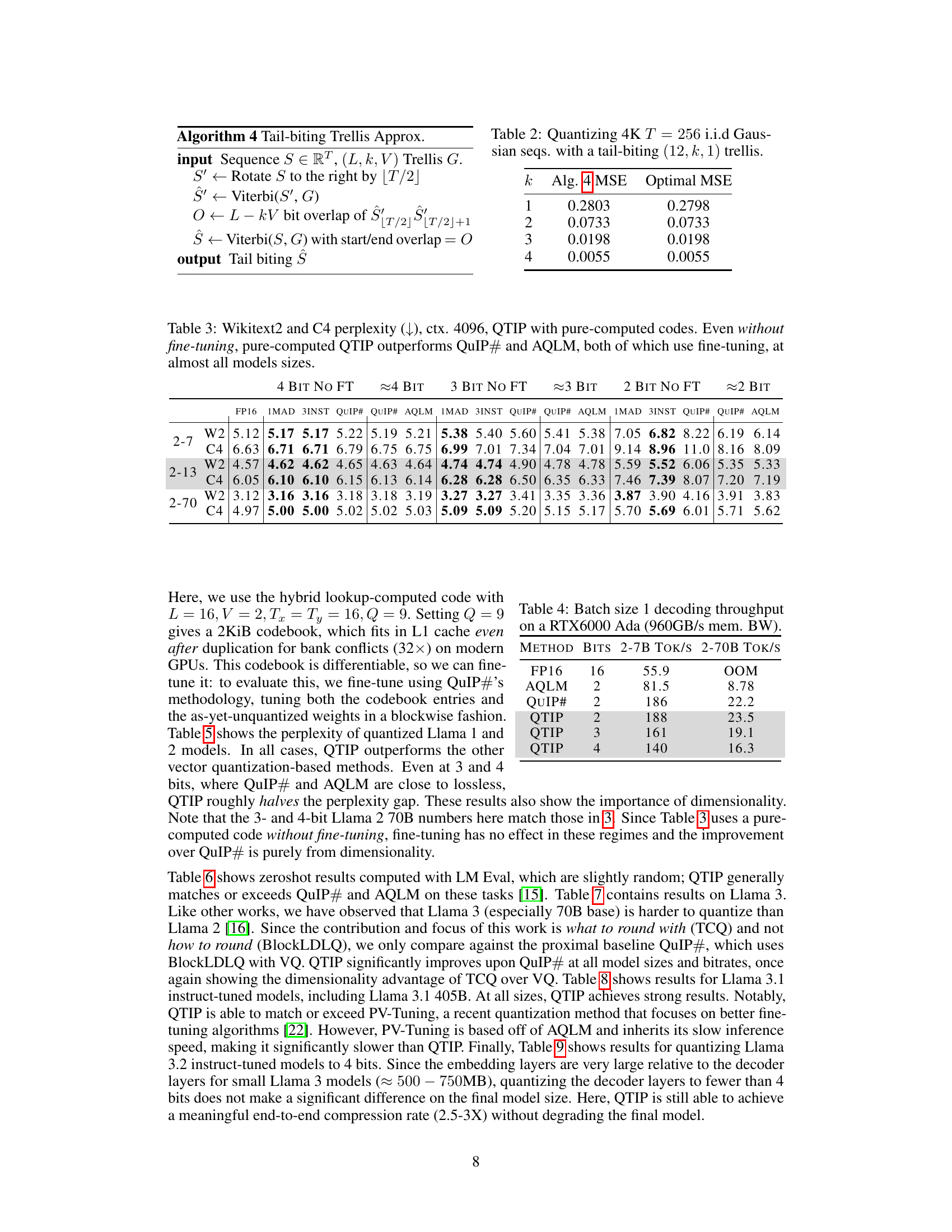
This table presents the results of quantizing 4096 independent and identically distributed (i.i.d.) Gaussian sequences of length 256 using a tail-biting trellis with various values of k (number of bits). It compares the Mean Squared Error (MSE) achieved by Algorithm 4 (a tail-biting trellis approximation algorithm) against the optimal MSE for each value of k. The results demonstrate the accuracy of Algorithm 4 in approximating the optimal MSE for tail-biting trellis quantization.
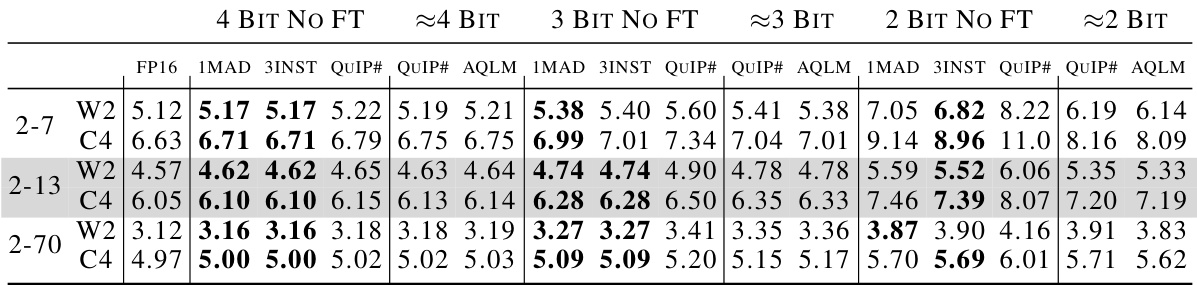
This table shows the Wikitext2 and C4 perplexity scores for different Llama model sizes (2-7B, 2-13B, and 2-70B) and bit depths (2, 3, and 4 bits). It compares the performance of QTIP’s pure computed codes (1MAD and 3INST) against QuIP# and AQLM. The results demonstrate that QTIP achieves lower perplexity scores (better performance) than QuIP# and AQLM even without fine-tuning, highlighting the effectiveness of QTIP’s approach.
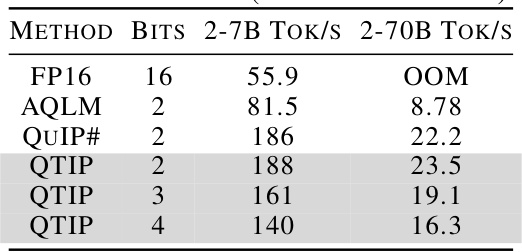
This table shows the inference speed of QTIP, QuIP#, and AQLM on Llama 2 7B and 70B models with matrix fusion. It demonstrates the significant speedups achieved by QTIP and QuIP# over FP16, highlighting QTIP’s ability to match QuIP#’s throughput with a much higher effective dimension.
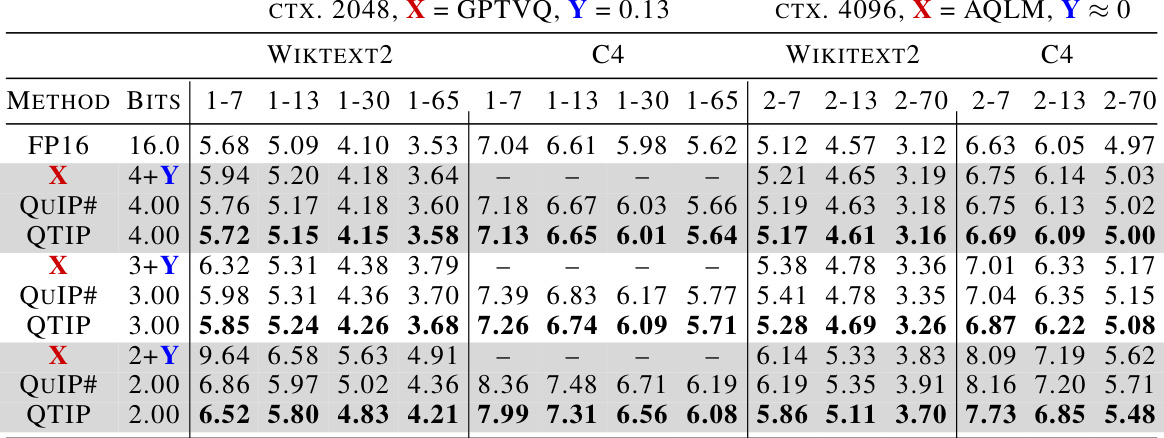
This table compares the performance of QTIP using pure compute-based codes (1MAD and 3INST) against QuIP# and AQLM on the Wikitext2 and C4 datasets. The results show that QTIP, even without the fine-tuning step used by QuIP# and AQLM, achieves significantly lower perplexity scores across various model sizes and bit depths (2-bit, 3-bit, and 4-bit). This demonstrates the effectiveness of QTIP’s compute-based codes in improving quantization quality.
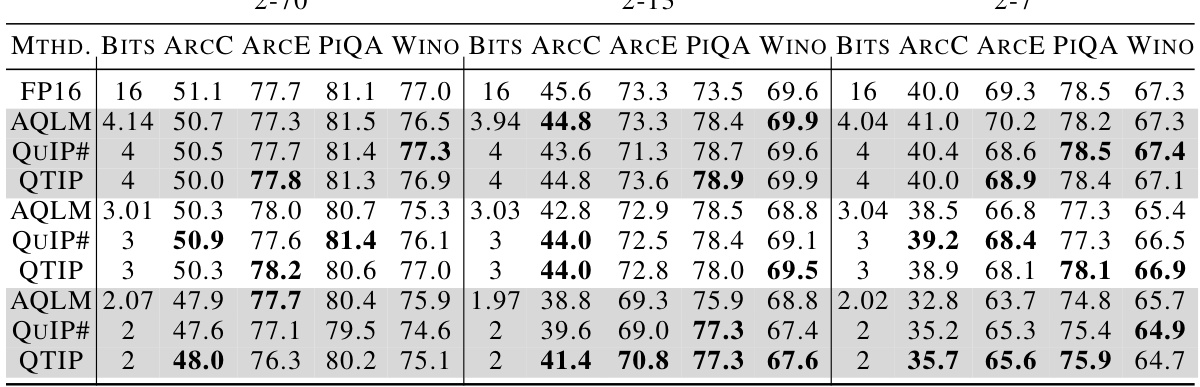
This table presents the results of experiments evaluating the performance of QTIP with pure-computed codes on the Wikitext2 and C4 datasets. It compares QTIP’s performance to QuIP# and AQLM, highlighting QTIP’s superior performance even without the fine-tuning used by the other methods. The results are broken down by model size and bit-depth.
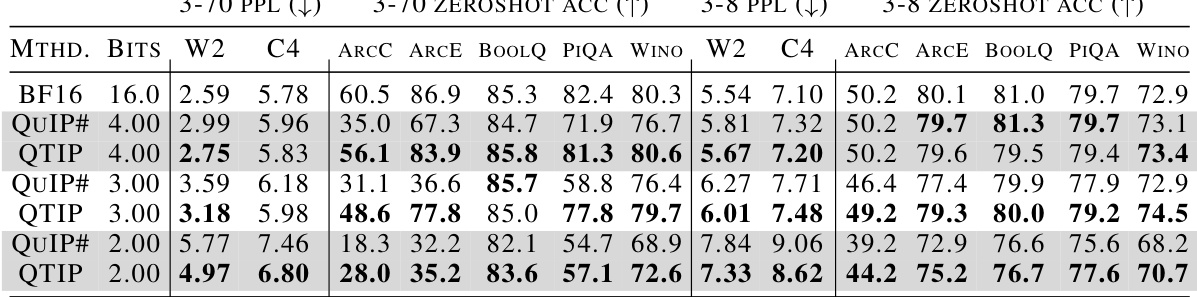
This table shows the results of using pure computed codes in QTIP on Wikitext2 and C4 datasets with a context size of 4096. The table compares the perplexity scores (lower is better) achieved by QTIP’s 1MAD and 3INST methods against QuIP# and AQLM across different bitrates (2, 3, 4 bits). The key finding is that QTIP significantly outperforms the other methods even without fine-tuning, showcasing the effectiveness of its compute-based codes.
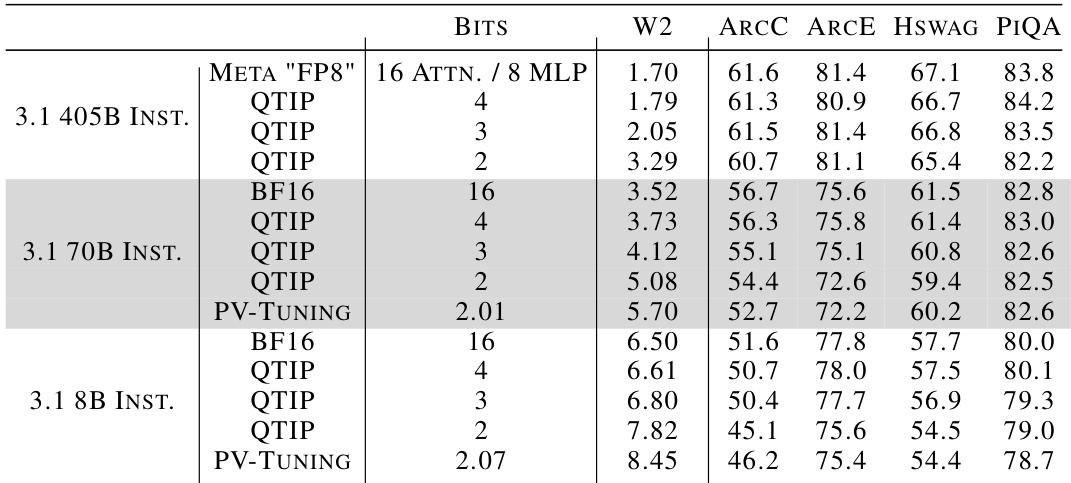
This table presents the results of experiments on the Wikitext2 and C4 datasets using QTIP with pure-computed codes. The results are compared to QuIP# and AQLM, which both use fine-tuning. The table shows that even without fine-tuning, QTIP achieves better perplexity scores (lower is better) across various model sizes and bit depths (2-bit, 3-bit, 4-bit). This demonstrates the effectiveness of QTIP’s pure-computed codes compared to fine-tuned VQ methods.
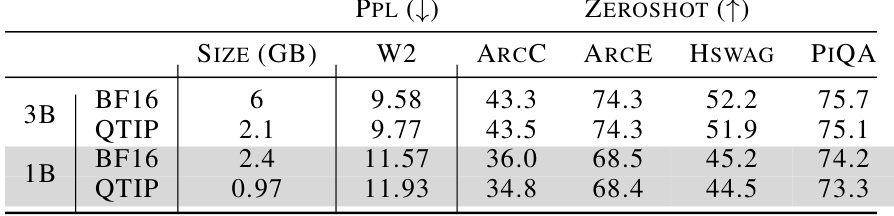
This table shows the results of quantizing Llama 3.2 instruct-tuned models to 4 bits, focusing on perplexity and zeroshot accuracy across various metrics (W2, ARCC, ARCE, HSWAG, PIQA). It highlights QTIP’s ability to maintain good performance even on smaller models, demonstrating effective compression without significant quality loss compared to the baseline FP16.
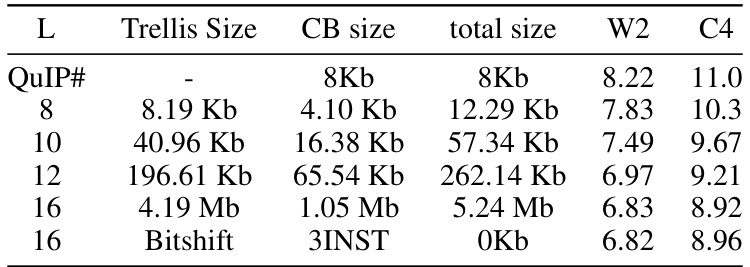
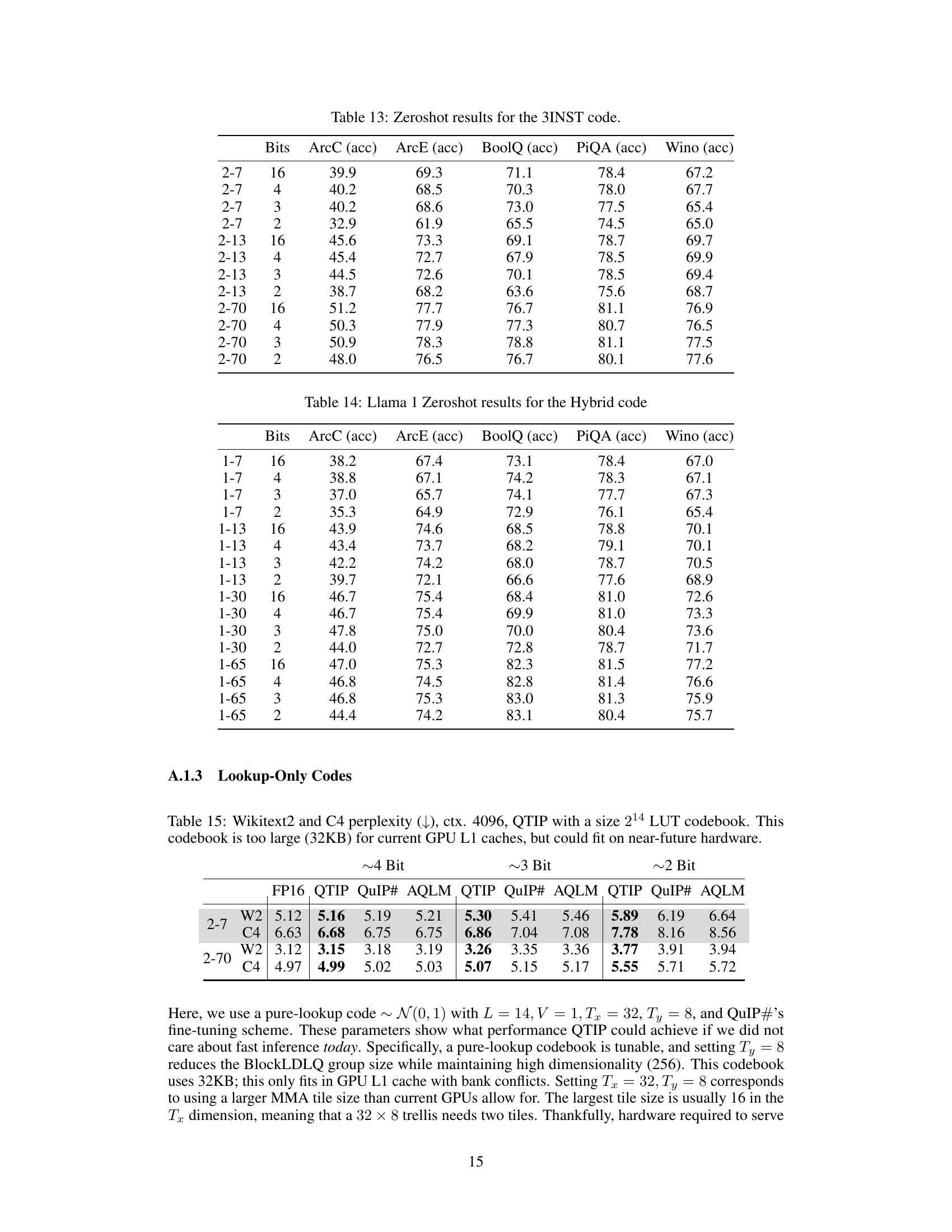
This table shows the results of an ablation study on the hyperparameter L (the length of the trellis) when quantizing the Llama 2 7B model to 2 bits. The experiment keeps K (the number of bits per edge) and V (the dimension of the vector quantized per trellis step) constant while varying L. The table shows the trellis size, codebook size, total size, and resulting perplexity on the Wikitext2 and C4 datasets for different values of L. This experiment helps to understand the impact of the trellis length on both model compression and performance.
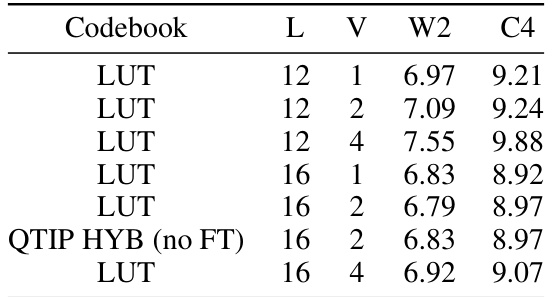
This table shows the results of an ablation study on the parameter V in the QTIP algorithm, while keeping other parameters constant (K=2, Llama 2 7B, 2-bit quantization). The study investigates how varying the length of subsequences (V) used in trellis-coded quantization affects the performance of the model, in terms of perplexity scores on Wikitext2 (W2) and C4 datasets. Different trellis lengths (L) are also considered.
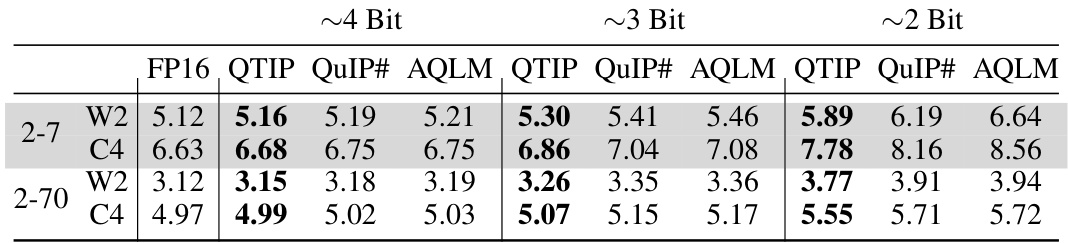
This table presents the results of experiments using pure-computed codes (1MAD and 3INST) in QTIP for quantizing the Wikitext2 and C4 datasets on Llama 2 models with context size of 4096. It compares QTIP’s performance against QuIP# and AQLM, highlighting QTIP’s superior performance even without fine-tuning, particularly at 2-bit quantization.
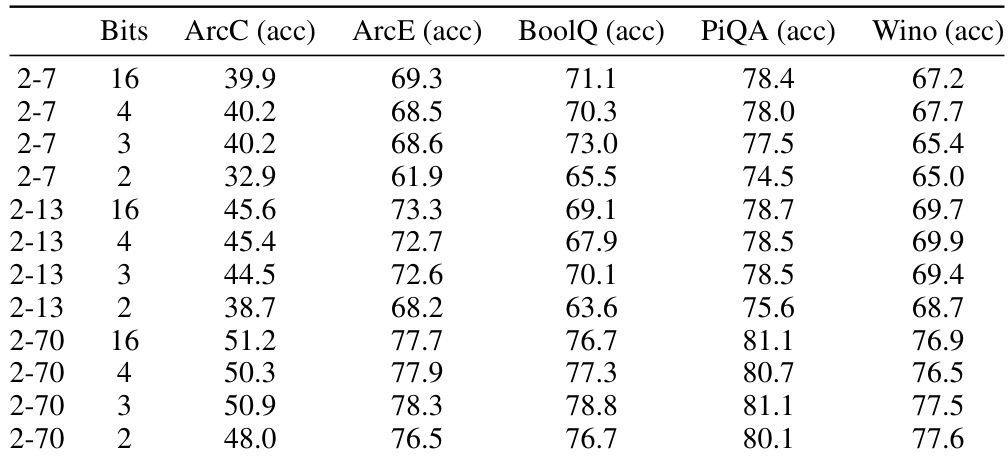
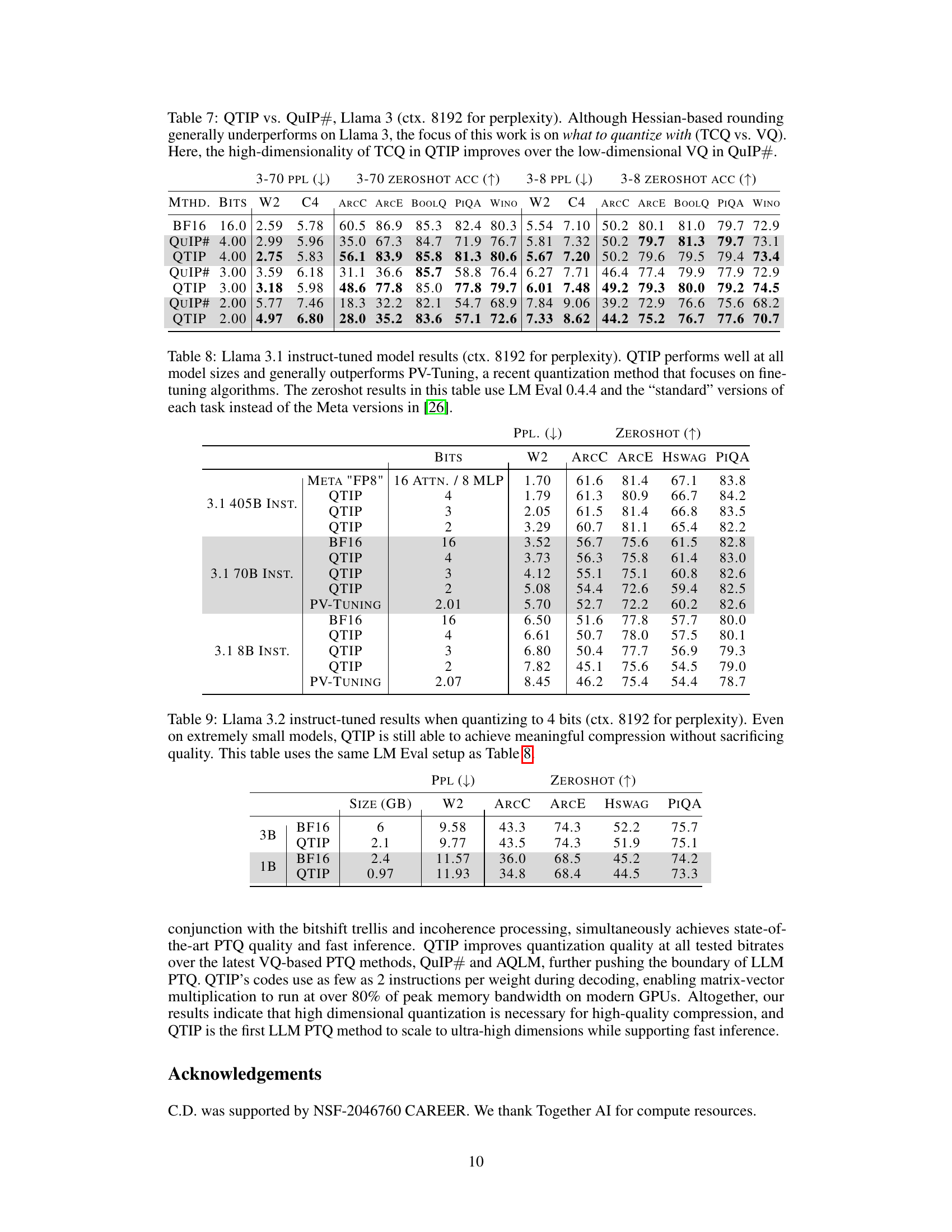
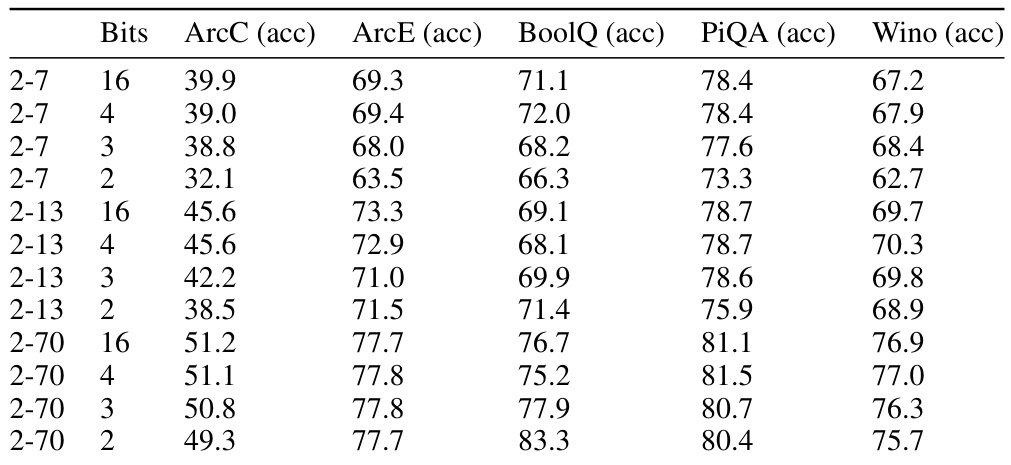
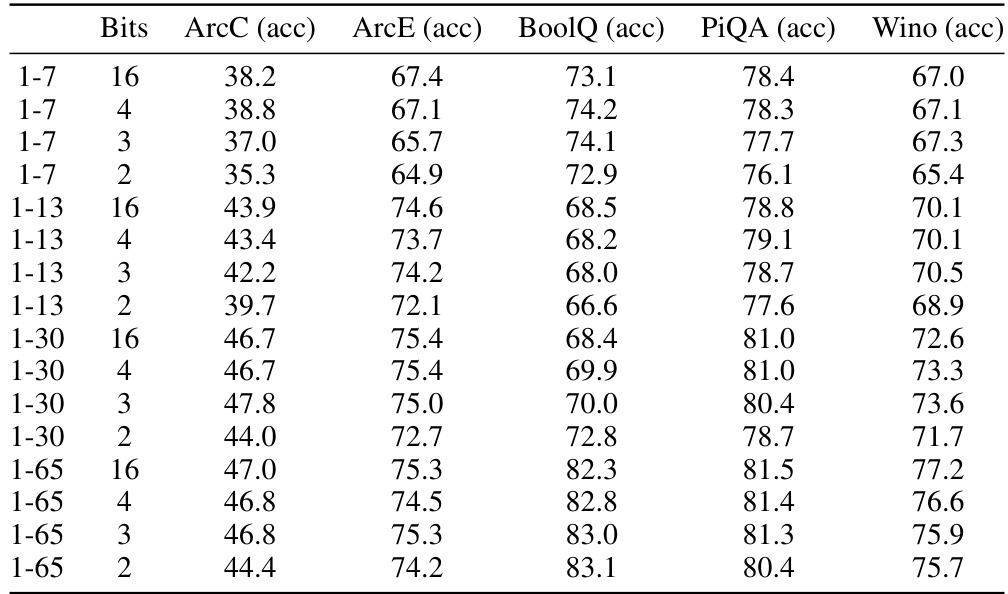
This table presents the zeroshot accuracy results obtained using the 3INST code for various bit depths (2, 3, 4, and 16 bits) and sequence lengths (7, 13, 30, 65, 70). The results are reported for five different tasks: ArcC, ArcE, BoolQ, PiQA, and Wino. The table shows how the performance of the 3INST code varies with the number of bits used and the length of the sequences, and also allows for comparison across different tasks.
This table shows the results of using pure-computed codes in QTIP for quantizing the Wikitext2 and C4 datasets with a context size of 4096. It compares the perplexity achieved by QTIP against QuIP# and AQLM, highlighting QTIP’s superior performance even without fine-tuning, which is a crucial step in other methods. The table demonstrates QTIP’s effectiveness across different model sizes and bit depths.
This table presents the results of using QTIP with the hybrid lookup-computed code on Wikitext2 and C4 datasets for different bit depths (2, 3, and 4 bits). It compares the perplexity achieved by QTIP against the baseline (FP16) and other state-of-the-art vector quantization methods, QuIP# and AQLM. Lower perplexity indicates better performance. The table demonstrates that QTIP consistently achieves lower perplexity scores than competing methods across various model sizes, showcasing its effectiveness in high-dimensional quantization.
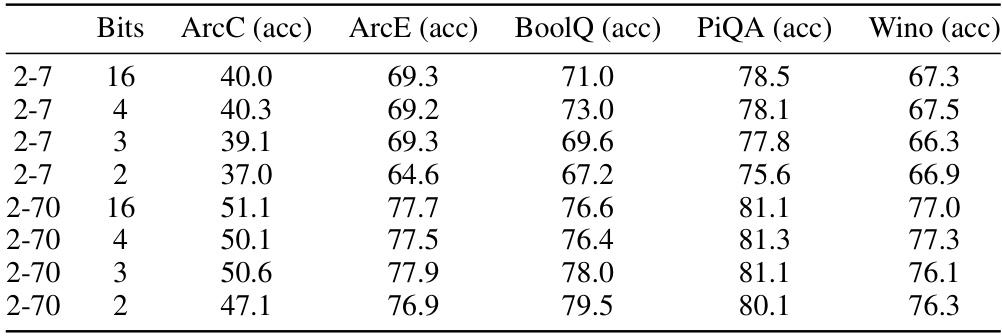
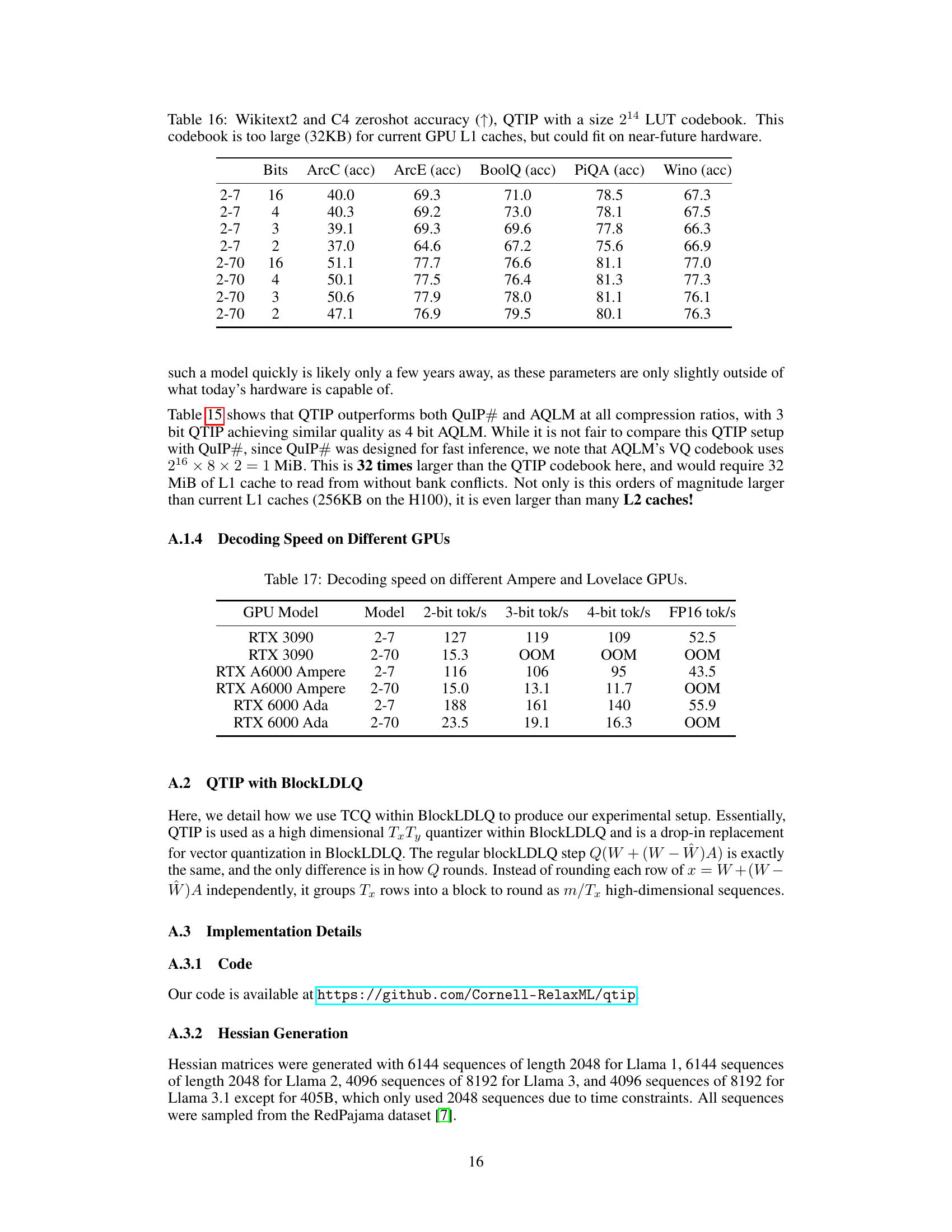
This table shows the zeroshot accuracy results on Wikitext2 and C4 datasets using QTIP with a 214 size LUT codebook. The codebook size is too large for current GPU L1 caches, but it’s suggested that this could be feasible with near-future hardware. The results are presented for different bit depths (2, 3, 4, and 16 bits) showing the performance of QTIP under these conditions and comparing it to other methods.
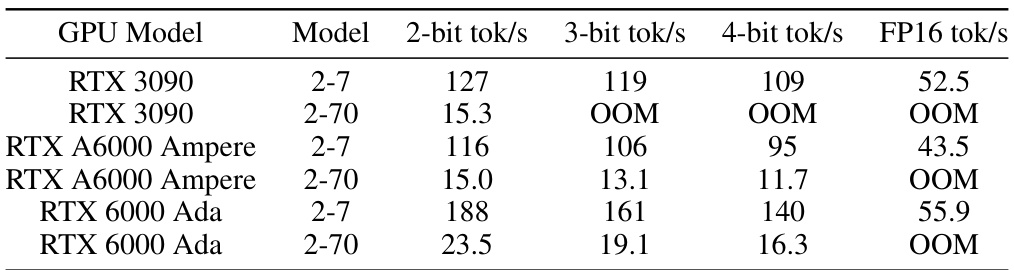
This table shows the decoding throughput for different Llama models (7B and 70B) quantized with different bit-widths (2, 3, and 4 bits) using various methods (AQLM, QuIP#, and QTIP). The throughput is measured in tokens per second (Tok/s) with batch size 1 on an RTX 6000 Ada GPU. It demonstrates the speed improvements achieved by QTIP and QuIP# over FP16 and AQLM, showcasing QTIP’s ability to maintain speed even with higher-dimensional quantization.
Full paper#