↗ OpenReview ↗ NeurIPS Proc. ↗ Hugging Face ↗ Chat
TL;DR#
Adapting large pre-trained models efficiently for downstream tasks is challenging due to high computational costs and memory requirements. Parameter-Efficient Fine-Tuning (PEFT) methods, such as Low-Rank Adaptation (LoRA) and Orthogonal Fine-Tuning (OFT), aim to reduce these costs by using limited trainable parameters. However, these methods often follow different principles, preventing a unified framework.
This paper introduces Householder Reflection Adaptation (HRA), a novel PEFT method that combines the strengths of LoRA and OFT. HRA adapts models by multiplying frozen weight matrices with an orthogonal matrix constructed by a chain of learnable Householder reflections, resulting in both orthogonal and adaptive low-rank adaptations. Experiments show that HRA outperforms existing methods on various tasks, including natural language understanding, mathematical reasoning, and image generation, with fewer trainable parameters.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working with large language models (LLMs) and image generation models because it introduces a novel and efficient adaptation method, HRA, that bridges the gap between low-rank and orthogonal adaptation techniques. This method offers superior performance with fewer trainable parameters, making it highly relevant to the current trend of optimizing parameter-efficient fine-tuning. Furthermore, HRA’s ability to retain pre-training knowledge while achieving effective adaptation opens up new avenues for future research in model adaptation.
Visual Insights#
This figure demonstrates the Householder Reflection Adaptation (HRA) method and compares its performance to other state-of-the-art methods. Subfigure (a) shows a schematic of the HRA method, illustrating how it adapts a pre-trained model by multiplying each frozen weight matrix with an orthogonal matrix constructed using a chain of Householder reflections. Subfigure (b) presents a comparison of HRA’s performance against other methods on the GLUE benchmark, showing superior performance with fewer parameters. Finally, subfigure (c) shows the performance comparison for mathematical reasoning tasks using LLaMA2-7B.

This table compares three different orthogonal fine-tuning (OFT) based adapter methods: OFT [37], BOFT [34], and the proposed Householder Reflection Adaptation (HRA). For each method, it illustrates the implementation, the number of parameters, the computational complexity, and whether it can cover the whole set of orthogonal matrices (Odxd). The table shows that HRA achieves comparable parameter efficiency and computational complexity to OFT and BOFT while offering a more flexible and potentially lower-complexity implementation.
In-depth insights#
HRA: Bridging the gap#
The heading “HRA: Bridging the Gap” suggests a central theme of reconciling two distinct approaches within a specific field. HRA likely represents a novel method that successfully integrates previously disparate techniques, potentially improving efficiency or effectiveness. This “bridging” implies overcoming limitations inherent in each of the original methods, offering a more robust or comprehensive solution. The success of HRA hinges on its ability to effectively combine the strengths of the underlying methodologies while mitigating their weaknesses. A key aspect would be the innovative way HRA merges these concepts, perhaps via a novel algorithm or architectural design. The resulting impact could range from improved performance on existing benchmarks to enabling new applications previously unattainable with either individual method.
Orthogonal Adaptation#
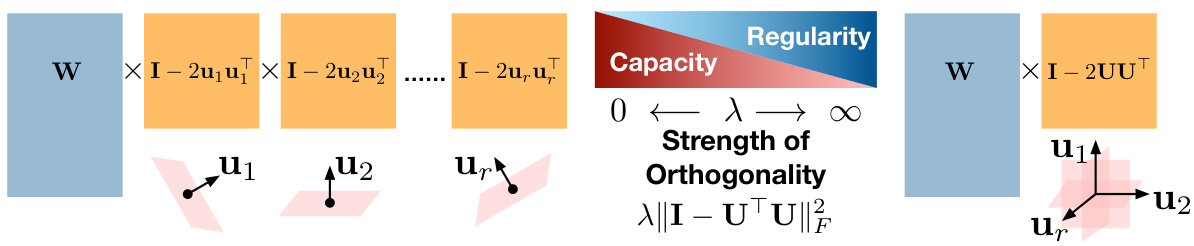
Orthogonal adaptation, in the context of large language model (LLM) fine-tuning, represents a parameter-efficient method that modifies pre-trained weights in a way that preserves their original orthogonality. This is in contrast to low-rank adaptation techniques which introduce low-rank updates. Maintaining orthogonality offers theoretical advantages, guaranteeing bounded discrepancy between pre-trained and adapted models, which can prevent catastrophic forgetting of pre-trained knowledge. However, ensuring strict orthogonality can limit model capacity. The exploration of methods that balance orthogonality and capacity, such as those using Householder reflections, is a key area of research, offering the potential for efficient and effective LLM adaptation across diverse tasks. This balance is crucial; while orthogonality protects pre-trained knowledge, too much can severely restrict expressiveness and prevent the model from learning new patterns effectively. Therefore, carefully managing the degree of orthogonality becomes a critical parameter in optimizing the performance of orthogonal adaptation methods.
HRA’s Capacity & Reg.#
The analysis of “HRA’s Capacity & Reg.” reveals a crucial trade-off inherent in the Householder Reflection Adaptation (HRA) method. Increasing the number of Householder reflections (r) enhances the model’s capacity, allowing it to learn more complex relationships within the data. However, this increase comes at the cost of potentially reducing the regularity of the model. The orthogonality of the reflection planes, controlled by the regularization parameter (λ), directly impacts this regularity. High orthogonality (large λ) enforces regularity, preserving the pre-trained model’s knowledge and preventing overfitting, but may limit the model’s capacity to adapt. Conversely, low orthogonality (small λ) allows greater capacity but risks instability and overfitting. Finding the optimal balance between capacity and regularity is crucial for achieving superior performance, and the study explores this by varying both r and λ. The experiments demonstrate that HRA effectively navigates this trade-off to obtain better results than existing methods, highlighting the method’s flexibility and effectiveness in model adaptation.
HRA vs. Existing OFT#
The comparison between HRA and existing orthogonal fine-tuning (OFT) methods reveals key distinctions in their implementation and performance. HRA’s use of Householder reflections provides a simpler, more computationally efficient approach compared to OFT and its variants (BOFT), which leverage more complex orthogonal matrix constructions. While OFT methods like BOFT strive for orthogonality through intricate transformations (e.g., butterfly factorization), HRA achieves a similar effect with a chain of simpler reflections, reducing both the number of trainable parameters and computational complexity. This efficiency advantage is particularly pronounced when adapting large models. Furthermore, HRA offers a flexible trade-off between model capacity and regularity by adjusting the orthogonality of its reflections via a regularization parameter. This allows HRA to potentially balance between retaining pre-training knowledge and effective task adaptation. The empirical results presented in the paper often demonstrate HRA’s superior performance with fewer parameters, showcasing the practical benefits of its streamlined approach.
Future of HRA#
The future of Householder Reflection Adaptation (HRA) looks promising, building upon its strengths in parameter efficiency and performance. Further research could focus on adaptive rank determination, moving beyond fixed r values, to optimize the trade-off between model capacity and computational cost. Investigating alternative regularizers beyond orthogonality could improve model robustness and generalization. Exploring HRA’s application in various model architectures beyond LLMs and image generators, and its potential for integration with other PEFT methods, is crucial. Addressing the computational cost for large models remains vital; optimization techniques and hardware acceleration should be explored. Finally, thorough investigation into HRA’s susceptibility to biases present in training data is needed to ensure responsible and ethical applications.
More visual insights#
More on figures

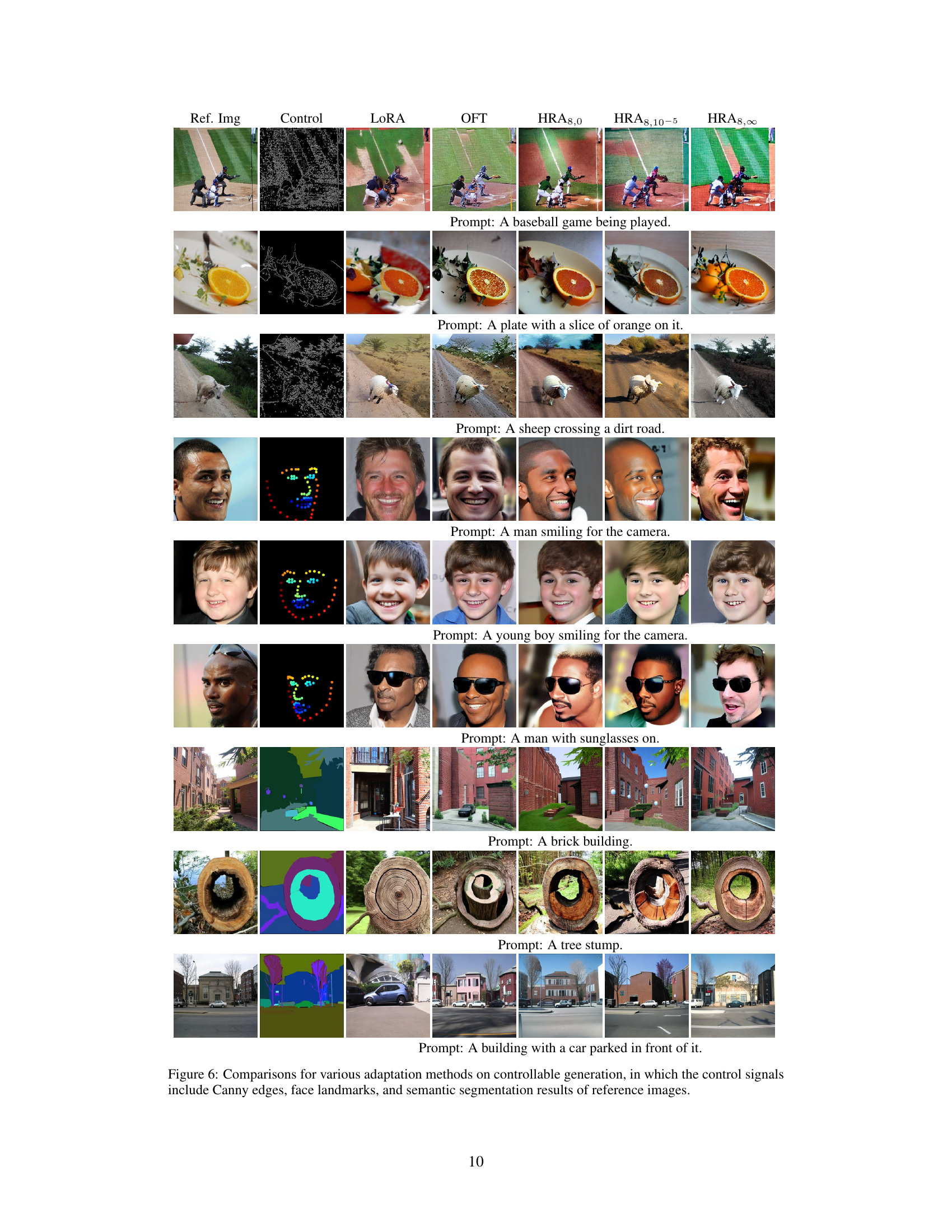
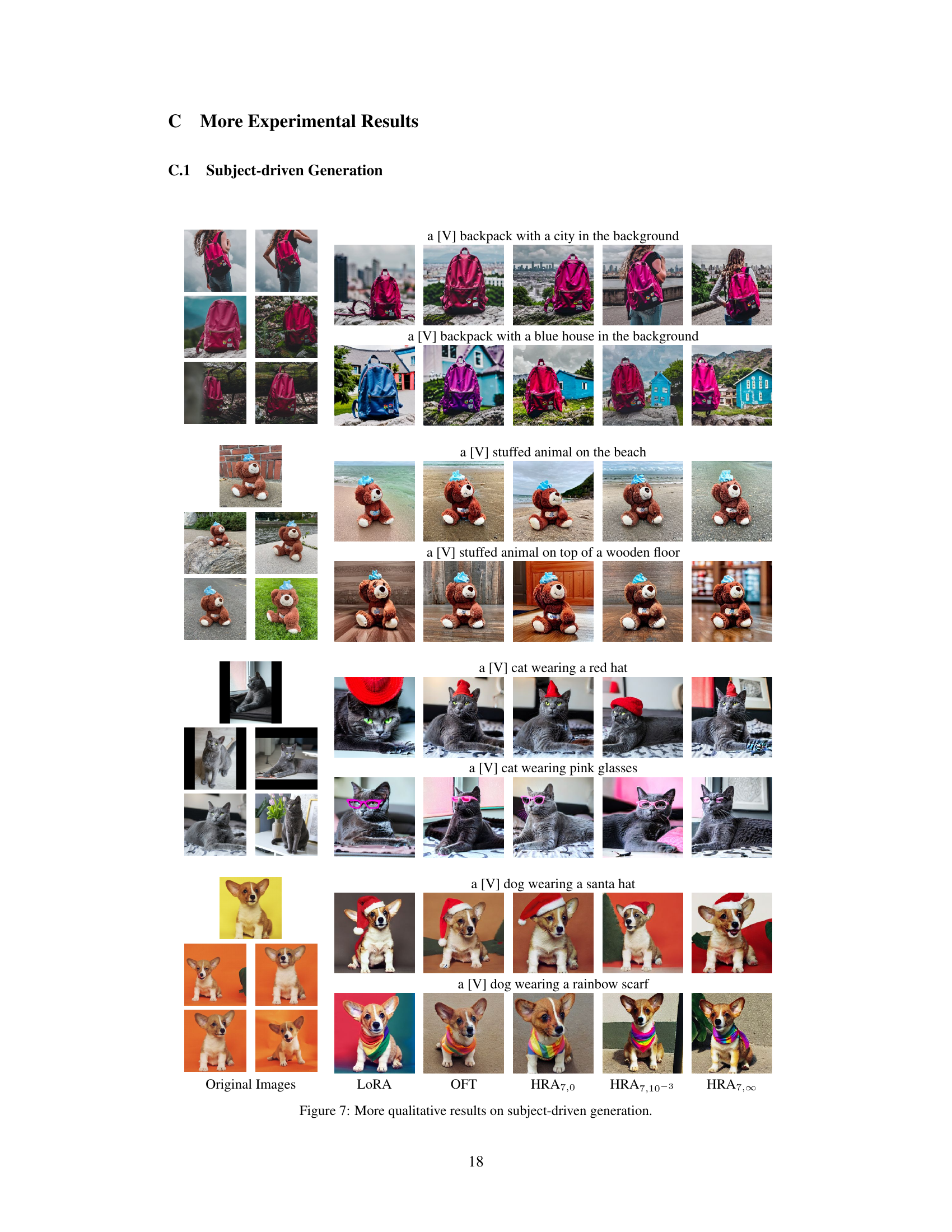
This figure presents a visual comparison of the proposed Householder Reflection Adaptation (HRA) method against other state-of-the-art methods. Panel (a) shows a schematic of the HRA approach, illustrating how it applies a series of Householder reflections to modify pre-trained model weights. Panel (b) compares HRA’s performance to other methods on the GLUE benchmark, plotting average GLUE score against the number of trainable parameters. Finally, Panel (c) shows a similar comparison of HRA’s performance on mathematical reasoning tasks, this time using LLaMA2-7B as the base model.

This figure presents a comprehensive evaluation of the proposed Householder Reflection Adaptation (HRA) method. Panel (a) illustrates the architecture of HRA, showing how it adapts a pre-trained model by multiplying its weight matrices with a chain of orthogonal matrices (Householder reflections). Panel (b) compares HRA’s performance against several state-of-the-art parameter-efficient fine-tuning (PEFT) methods on the GLUE benchmark, demonstrating superior performance with fewer trainable parameters. Panel (c) shows a similar comparison for adapting a large language model (LLaMA2-7B) on mathematical reasoning tasks, reinforcing HRA’s effectiveness.
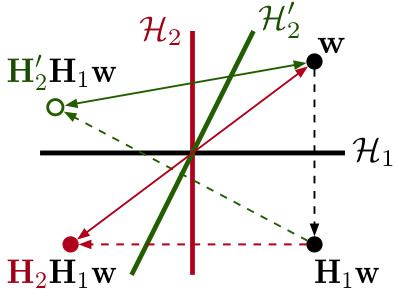
This figure illustrates the impact of orthogonality on the effectiveness of the Householder Reflection Adaptation (HRA) method. It shows a 2D representation of the effect of applying two successive Householder reflections (H1 and H2) to a weight vector w. When the reflection planes (hyperplanes) defined by H1 and H2 are orthogonal, the resulting vector H2H1w is maximally distant from the original vector w. This maximal distance implies that the HRA method can maximize the adaptation capacity when the reflection planes are orthogonal. The non-orthogonal case (dashed lines) is also shown for comparison, highlighting that the distance is smaller when the planes are not orthogonal. This supports the paper’s argument that orthogonality of Householder reflections influences model capacity.

This figure displays the robustness of the Householder Reflection Adaptation (HRA) method, with r=8, to variations in the orthogonality regularizer (λ) when evaluated on the MRPC (Microsoft Research Paraphrase Corpus) dataset. The x-axis represents the values of λ, ranging from 10⁻⁷ to 10⁻³, and the y-axis shows the accuracy achieved on the MRPC task. The bars show that the performance of HRA remains relatively stable across a wide range of λ values, indicating its robustness to variations in this hyperparameter.

This figure contains three subfigures. Subfigure (a) shows the architecture of the Householder Reflection Adaptation (HRA) method, illustrating how it modifies the weight matrix of a pre-trained model by multiplying it with a chain of Householder reflections. Subfigure (b) presents a comparison of HRA’s performance against other state-of-the-art parameter-efficient fine-tuning (PEFT) methods on the GLUE benchmark. It shows that HRA achieves superior performance with fewer parameters. Subfigure (c) displays a comparison of different PEFT methods, including HRA, on mathematical reasoning tasks using the LLaMA2-7B model. It further demonstrates HRA’s efficiency in adapting large language models.

This figure consists of three subfigures. Subfigure (a) illustrates the architecture of the proposed Householder Reflection Adaptation (HRA) method, showing how it adapts a pre-trained model by multiplying its weight matrices with orthogonal matrices constructed using a chain of Householder reflections. Subfigure (b) presents a comparison of HRA’s performance against other state-of-the-art parameter-efficient fine-tuning (PEFT) methods on the GLUE benchmark, plotting average accuracy against the number of trainable parameters. Lastly, subfigure (c) shows a similar comparison but specifically for adapting the LLaMA2-7B model on mathematical reasoning tasks.
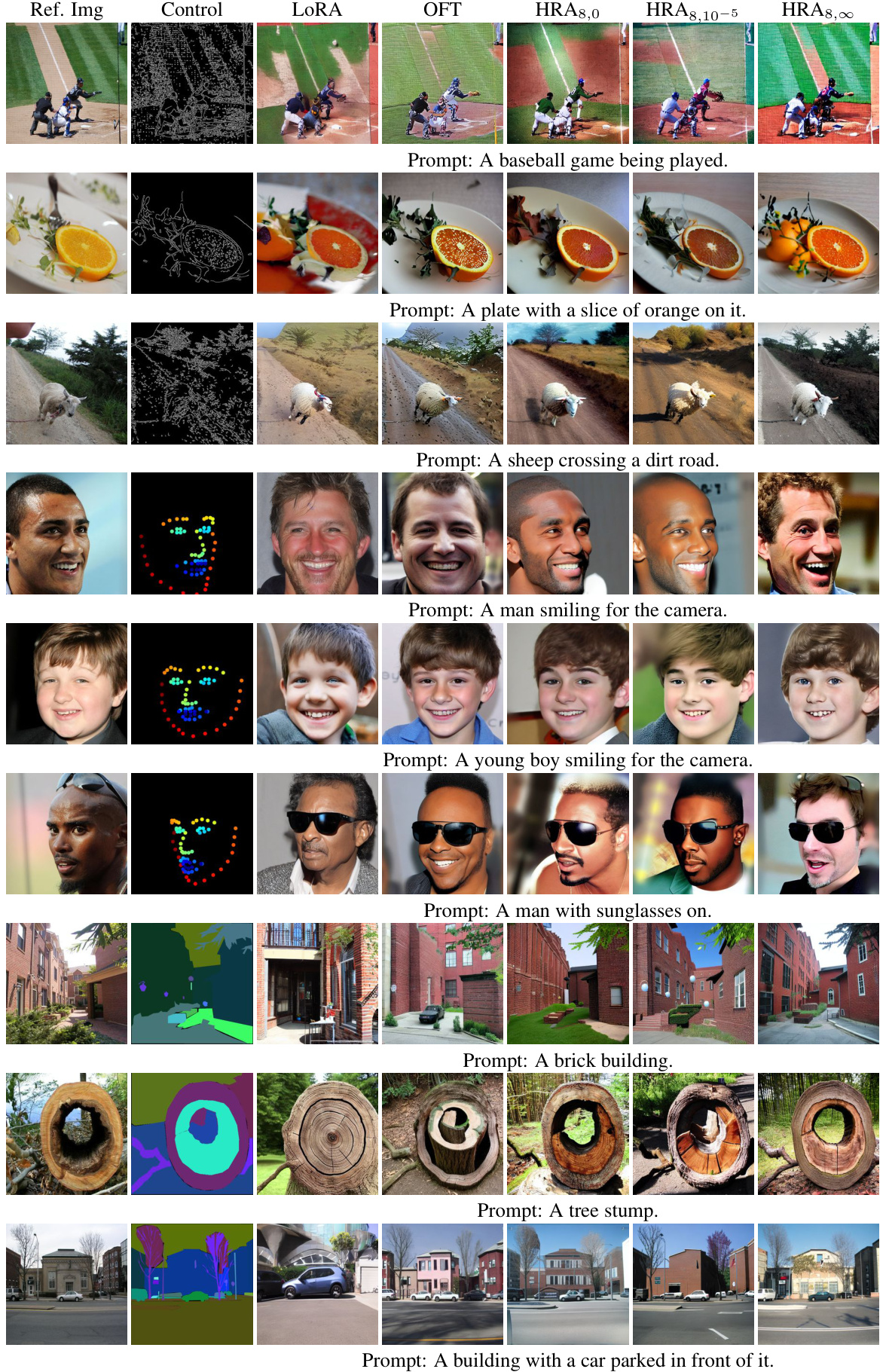
This figure presents a comparison of the proposed Householder Reflection Adaptation (HRA) method with other state-of-the-art methods for model adaptation. Subfigure (a) shows a schematic of the HRA method, illustrating its mechanism using Householder reflections. Subfigure (b) displays a performance comparison on the GLUE benchmark, plotting average scores against the number of trainable parameters. Finally, subfigure (c) shows a similar comparison, but specifically for adapting the LLaMA2-7B model for mathematical reasoning tasks.

This figure presents a comparison of the proposed Householder Reflection Adaptation (HRA) method with other state-of-the-art methods for model adaptation. Subfigure (a) illustrates the HRA method’s architecture, showing how it multiplies a pre-trained weight matrix with a chain of orthogonal matrices constructed by Householder reflections. Subfigure (b) shows the performance comparison on the GLUE benchmark, highlighting HRA’s superior performance with fewer trainable parameters. Finally, subfigure (c) shows the performance comparison on mathematical reasoning tasks using LLaMA2-7B, again demonstrating HRA’s efficiency and effectiveness.

This figure shows three subfigures. Subfigure (a) illustrates the architecture of the proposed Householder Reflection Adaptation (HRA) method. Subfigure (b) presents a comparison of the performance of HRA against other state-of-the-art methods on the GLUE benchmark dataset, showing the average score on the y-axis against the number of trainable parameters on the x-axis. Subfigure (c) provides a similar comparison, but this time for adapting the LLaMA2-7B model to perform mathematical reasoning tasks.

This figure presents a comparison of the proposed Householder Reflection Adaptation (HRA) method with other state-of-the-art parameter-efficient fine-tuning methods. Subfigure (a) illustrates the mechanism of HRA, showing how it adapts a pre-trained model by multiplying each weight matrix with an orthogonal matrix created by a chain of Householder reflections. Subfigure (b) shows a performance comparison on the GLUE benchmark, plotting average accuracy against the number of trainable parameters, demonstrating HRA’s efficiency and effectiveness. Finally, subfigure (c) presents a similar comparison focusing on adapting LLaMA2-7B for mathematical reasoning tasks.

This figure presents a comprehensive overview of the Householder Reflection Adaptation (HRA) method proposed in the paper. Subfigure (a) illustrates the architectural scheme of HRA, which involves multiplying frozen weight matrices by an orthogonal matrix constructed from a chain of Householder reflections. Subfigure (b) compares the performance of HRA with other state-of-the-art parameter-efficient fine-tuning methods on the GLUE benchmark, highlighting HRA’s superior performance with fewer trainable parameters. Finally, subfigure (c) demonstrates HRA’s effectiveness in adapting large language models (LLMs) for mathematical reasoning tasks, showcasing its performance advantage in terms of both accuracy and parameter efficiency compared to competing methods.

This figure presents a comparison of different parameter-efficient fine-tuning (PEFT) methods. Subfigure (a) illustrates the Householder Reflection Adaptation (HRA) method, showing how it modifies the weight matrix of a pre-trained model. Subfigures (b) and (c) show performance comparisons on the GLUE benchmark and mathematical reasoning tasks, respectively, demonstrating HRA’s effectiveness in adapting large language models with fewer parameters and achieving higher accuracy.
More on tables
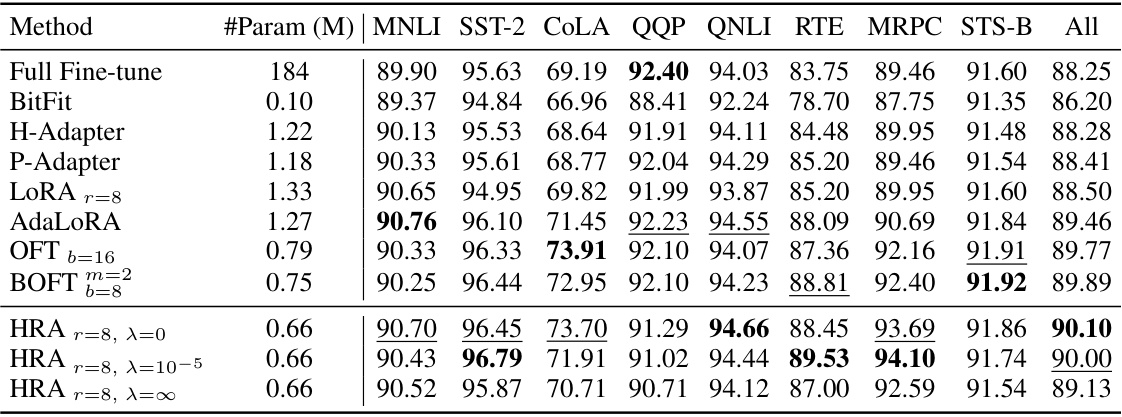
This table presents the performance comparison of different parameter-efficient fine-tuning (PEFT) methods on the GLUE benchmark dataset. It shows the average score achieved by each method across eight different GLUE tasks, along with the number of trainable parameters used. The best and second-best results for each task are highlighted.

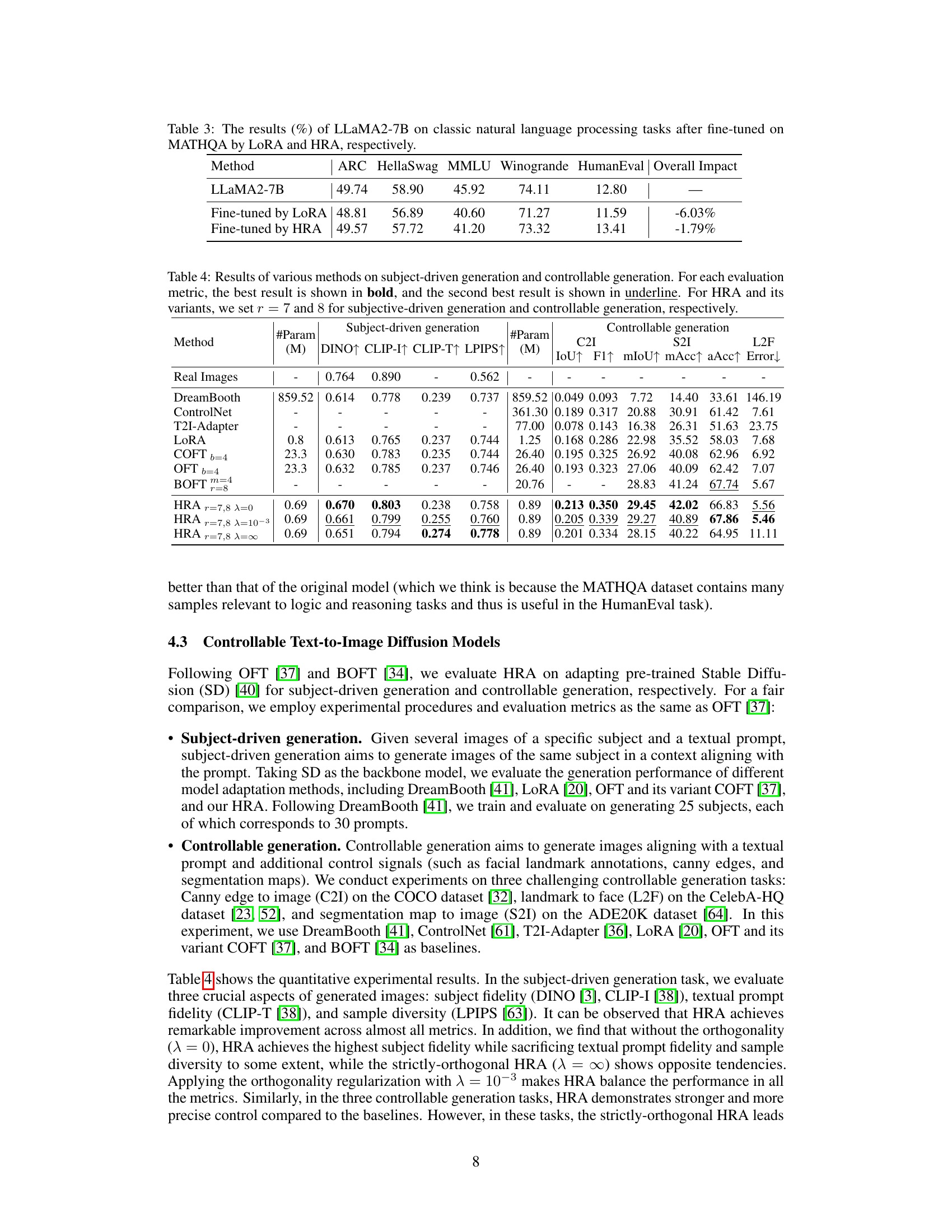
This table presents the performance of LLaMA2-7B on various natural language processing tasks after fine-tuning with LoRA and HRA methods. The tasks include ARC, HellaSwag, MMLU, Winogrande, and HumanEval. The ‘Overall Impact’ column shows the percentage change in performance compared to the original LLaMA2-7B model. The table highlights that HRA demonstrates less performance degradation after fine-tuning on MATHQA compared to LoRA, indicating better preservation of pre-training knowledge.
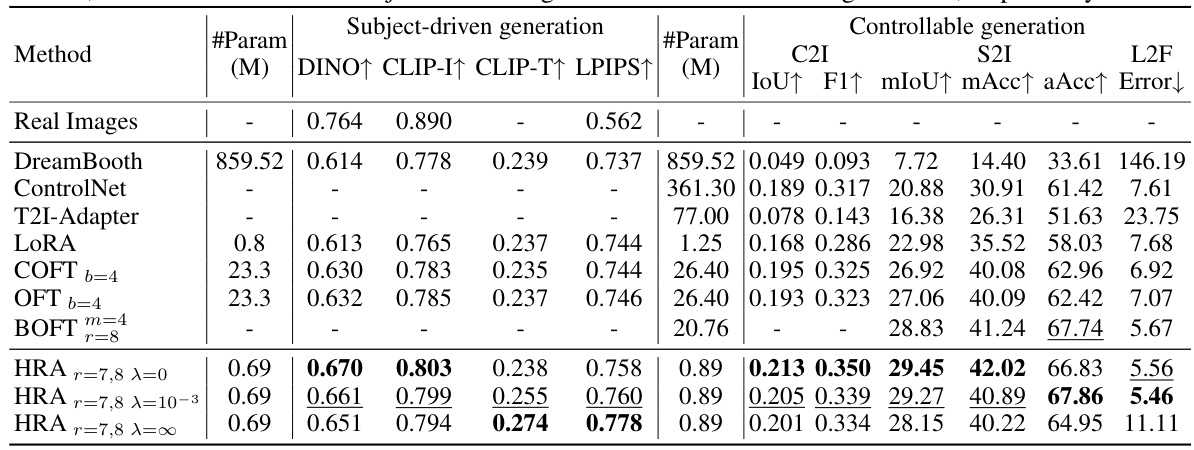
This table compares three different orthogonal fine-tuning (OFT) based adapter methods: OFT, BOFT, and the proposed HRA method. For each method, it shows the implementation details (using illustrations), the number of trainable parameters, the computational complexity and the model capacity. The table helps to illustrate the differences and similarities between these OFT based methods in terms of their efficiency and capacity.
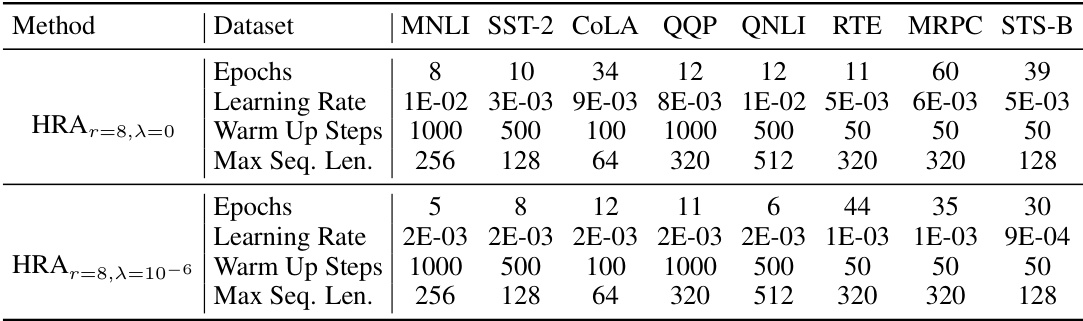
This table shows the hyperparameters used for training the DeBERTaV3-base model on the GLUE benchmark using the HRA method. Specifically, it lists the number of epochs, learning rate, warm-up steps, and maximum sequence length for each of the eight GLUE tasks: MNLI, SST-2, CoLA, QQP, QNLI, RTE, MRPC, and STS-B. Two different sets of hyperparameters are shown, representing variations of the HRA method with and without orthogonality regularization.

This table compares the computational efficiency of different model adaptation methods, including LoRA, OFT, and HRA, when adapting the LLaMA2-7B model on the MetaMathQA dataset. It shows the parameter ratio (percentage of trainable parameters relative to the original model size), training time (in hours), and peak memory usage (in GB). The results indicate the relative efficiency and memory requirements of each method.

This table compares three different orthogonal fine-tuning (OFT)-based adapter methods: OFT [37], BOFT [34], and the proposed Householder Reflection Adaptation (HRA). For each method, it shows the implementation details, the number of parameters, and the computational complexity. It highlights the differences in how these methods construct orthogonal matrices and their implications for model size and efficiency. The illustration section uses diagrams to visualize the structure of the matrices for each method.
Full paper#