↗ OpenReview ↗ NeurIPS Proc. ↗ Hugging Face ↗ Chat
TL;DR#
Large language models (LLMs) are increasingly used but prone to producing false information, known as hallucinations. Creating reliable truthfulness classifiers is difficult due to the lack of large, labeled datasets of truthful and false statements. Existing methods often require extensive human annotation or rely on assumptions about the nature of hallucinations.
HaloScope offers a novel solution by using unlabeled LLM outputs. It automatically estimates whether an LLM’s output is truthful or false. This is achieved through a subspace identification method. The method significantly outperforms existing approaches, demonstrating superior accuracy and efficiency in various benchmark tests. It introduces a practical and adaptable framework for hallucination detection, particularly valuable in real-world scenarios with limited labeled data.
Key Takeaways#
Why does it matter?#
This paper is important because it introduces a novel method for detecting AI hallucinations that doesn’t require large labeled datasets; a significant challenge in the field. This opens up new avenues of research, especially in real-world applications of large language models where labeled data is scarce.
Visual Insights#

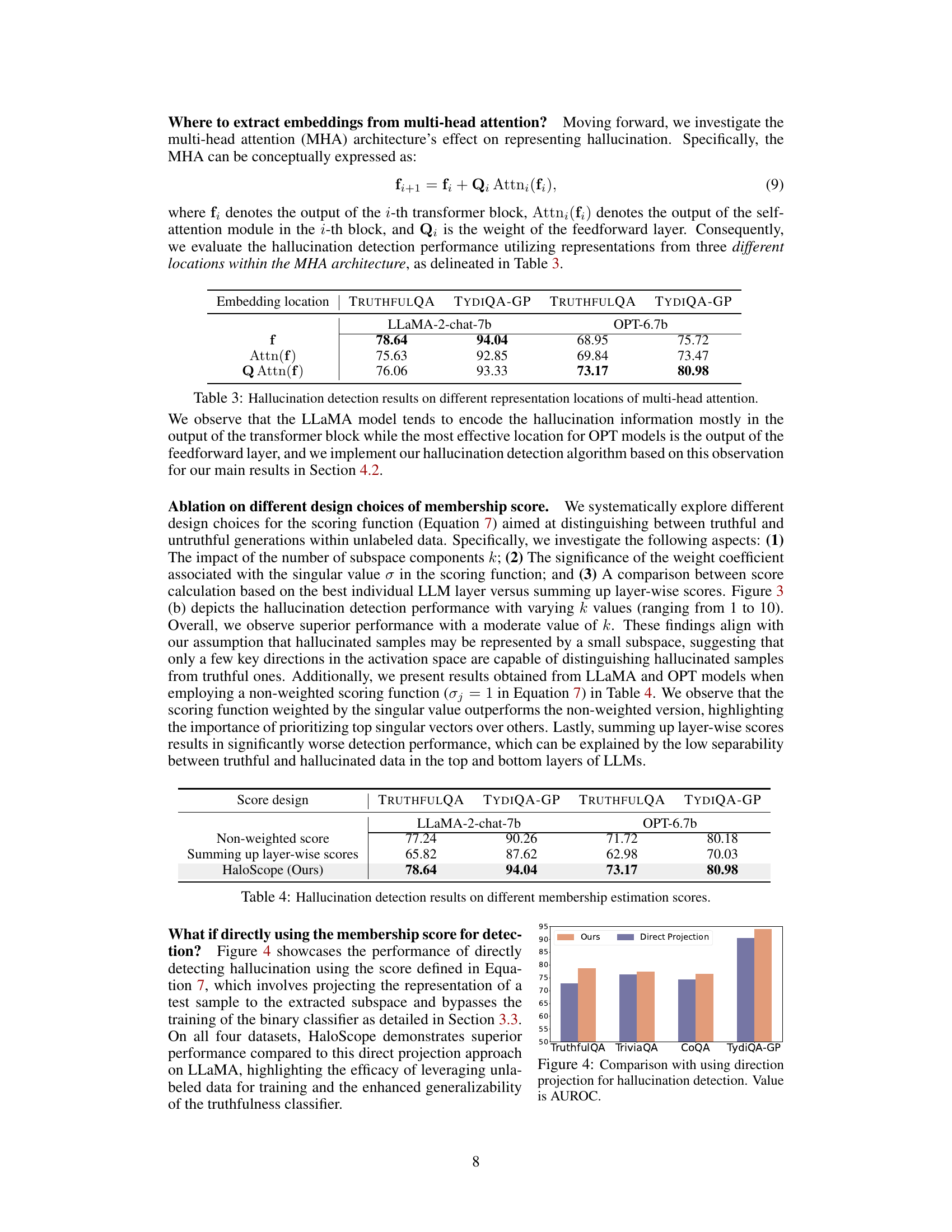
This figure illustrates the HaloScope framework. Unlabeled data from an LLM, containing both truthful and hallucinated responses to prompts, is input. HaloScope then identifies a latent subspace representing hallucinated responses. Based on the proximity of a new response to this subspace, a membership estimation score is generated. Finally, a binary classifier is trained to distinguish between truthful and hallucinated content using this score.
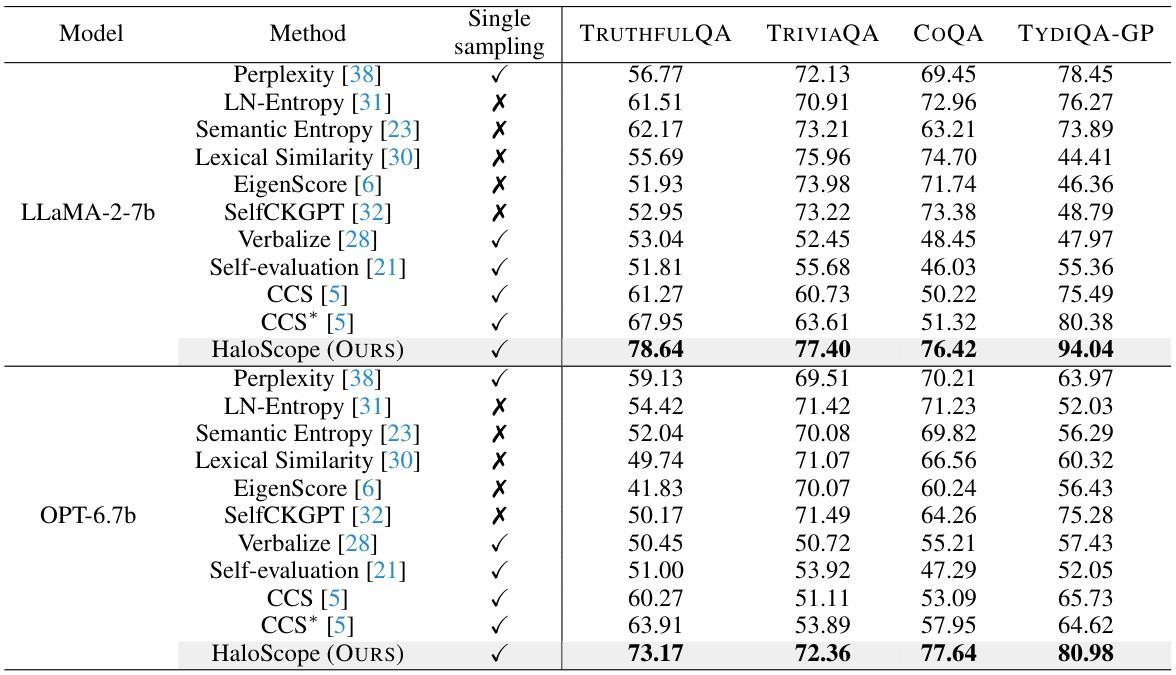
This table presents the Area Under the ROC Curve (AUROC) scores for various hallucination detection methods across four different datasets. The methods are categorized into several approaches (uncertainty-based, consistency-based, prompting-based, and knowledge discovery-based) and compared against the proposed HaloScope method. The table shows the performance of each method on two different language models (LLaMA-2-7b and OPT-6.7b) and indicates whether the method requires multiple generations during inference.
In-depth insights#
Unlabeled Data Use#
The use of unlabeled data is a critical innovation in this research. By cleverly leveraging readily available, unlabeled LLM outputs, the authors sidestep the significant hurdle of acquiring expensive, human-labeled datasets for hallucination detection. This approach is highly practical, offering flexibility and scalability compared to traditional methods. The core methodology involves using the unlabeled data to identify a latent subspace associated with hallucinated outputs. This subspace is then used to train a binary classifier, effectively distinguishing between truthful and false LLM generations. Automated membership estimation is key, allowing the model to effectively categorize unlabeled instances. The results highlight the substantial performance gains achieved using this unlabeled data approach and demonstrate the potential for significantly improving hallucination detection in real-world applications.
Subspace Detection#
Subspace detection, in the context of hallucination detection within large language models (LLMs), offers a powerful technique to identify patterns indicative of untruthful or fabricated information. By analyzing the high-dimensional embedding space of LLM outputs, a subspace can be identified that strongly correlates with instances of hallucinations. This subspace represents a cluster of data points whose features deviate significantly from those of truthful generations. The key insight is that hallucinations, despite their surface coherence, tend to exhibit systematic distortions in their internal representations that distinguish them from factually accurate outputs. HaloScope leverages this by identifying the low-dimensional subspace characterizing such distortions, enabling the estimation of a membership score. This score quantifies the proximity of a given LLM output to the hallucination subspace, effectively providing a measure of its truthfulness. This approach demonstrates the potential of harnessing intrinsic model characteristics to discern truthfulness without relying on explicit labels, a significant advantage in the face of scarce labeled data. The effectiveness of subspace detection rests on the ability of the LLM’s internal representations to implicitly capture semantic information associated with factuality. Successful identification of this subspace is crucial for robust performance and highlights the interplay between LLM architecture, data characteristics, and the efficacy of the detection method. The practical implications extend to real-world deployments, suggesting subspace detection may offer a more efficient and scalable path for ensuring LLM reliability. Further research could explore the robustness of the identified subspace across various LLMs, data domains, and prompt types.
Truthfulness Classifier#
The proposed truthfulness classifier is a crucial component of the HaloScope framework, designed to distinguish between truthful and hallucinated LLM generations. The classifier leverages the output of a membership estimation score, which quantifies the likelihood of a generation being a hallucination based on its alignment with a hallucination subspace identified within LLM embeddings. This clever approach bypasses the need for labeled data, a significant limitation in prior work. The classifier’s training focuses on separating hallucinated samples from a set of candidate truthful samples, avoiding a costly manual labeling process. The effectiveness is demonstrated through strong performance on multiple datasets, highlighting the power of HaloScope’s unlabeled data approach. The choice of loss function (sigmoid loss) ensures smoothness and tractability, facilitating efficient training. Ultimately, the classifier’s accuracy and generalization capabilities underscore the innovative and practical value of HaloScope in addressing the challenge of hallucination detection in large language models.
Robustness and Limits#
A robust model should generalize well to unseen data and various conditions. The paper’s discussion of robustness would likely explore the model’s performance across different datasets, model sizes, and data distributions. Generalization ability is key; a robust model shouldn’t overfit to training data. Sensitivity to hyperparameter choices is another aspect; a truly robust model should exhibit consistent performance across reasonable variations in hyperparameter settings. Limitations would address the model’s boundaries. This could include scenarios where the model fails—e.g., with extremely noisy data, adversarial examples, or tasks outside its intended scope. Computational cost is another key consideration. The analysis would consider whether the technique remains efficient and scalable when applied to massive datasets or more complex scenarios. Ethical implications should also be addressed: Are there potential biases that could surface? Does the model exhibit unwanted behavior in specific contexts? Addressing robustness and limits provides a well-rounded assessment of the model’s practicality and reliability.
Future Work#
The authors suggest several promising avenues for future research. Improving the robustness of HaloScope to distribution shifts between unlabeled training data and real-world test data is paramount. This could involve exploring more advanced domain adaptation techniques or developing more sophisticated methods for estimating membership scores that are less sensitive to data variations. Another key area is investigating different strategies for training the truthfulness classifier. While the binary classifier used in HaloScope is effective, alternative approaches, such as multi-class classification or more advanced learning paradigms, could potentially yield improvements in performance. Finally, expanding the scope of HaloScope to encompass different LLM architectures and a wider array of tasks is crucial. Evaluating its effectiveness on diverse languages and modalities beyond text will help determine its broader applicability and generalizability. Addressing these aspects would solidify HaloScope’s position as a robust and widely applicable hallucination detection method.
More visual insights#
More on figures
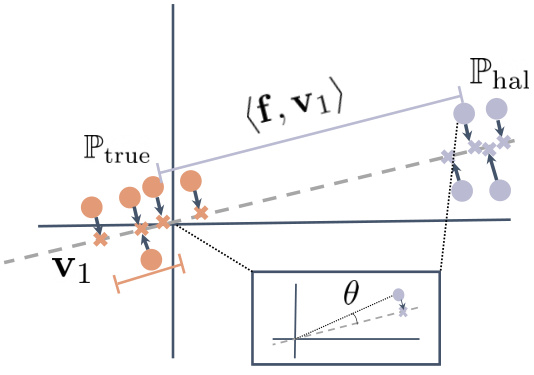
This figure visually represents the core idea behind HaloScope’s membership estimation. It shows two distinct clusters of data points, representing truthful (orange) and hallucinated (purple) LLM generations. Each point is an embedding vector from a language model. A line (v1, the top singular vector) is drawn through the origin, representing the subspace identified by HaloScope that best separates these two clusters. The distance from each data point to this line (its projection onto the line) is used as the membership score. Hallucinated samples tend to project farther from the origin along v1 than truthful samples, making it possible to distinguish them based on their projection.

This figure demonstrates three key aspects of the HaloScope framework. (a) shows the model’s ability to generalize across different datasets. The source dataset is used to extract a subspace, which is then applied to other target datasets. The results indicate strong transferability. (b) explores the impact of the number of subspace components (k) on the model’s performance. The AUROC is plotted against different values of k, showing that a moderate number of components leads to optimal results. (c) investigates the effectiveness of using different layers of the LLM for subspace extraction. Performance varies across different layers, highlighting the importance of choosing the optimal layer for embedding feature extraction.

This figure compares the performance of HaloScope with a simpler method that directly uses the membership score for hallucination detection, without training a binary classifier. The simpler method involves projecting the representation of a test sample onto the extracted subspace. The bar chart shows the AUROC scores for both methods across four datasets: TRUTHFULQA, TriviaQA, COQA, and TydiQA-GP. HaloScope consistently outperforms the direct projection approach, demonstrating the effectiveness of leveraging unlabeled data for training a more generalizable truthfulness classifier.

This figure compares the performance of HaloScope with a supervised oracle (trained on labeled data) for hallucination detection. The results show that HaloScope achieves comparable performance to the supervised oracle on the TRUTHFULQA dataset (AUROC of 78.64% vs. 81.04%). This demonstrates that HaloScope’s accuracy in detecting hallucinations is quite high, especially considering it does not rely on manual annotations. The bar chart presents AUROC scores for both HaloScope and the labeled data approach across four datasets: TRUTHFULQA, TriviaQA, COQA, and TydiQA-GP.

This figure illustrates the HaloScope framework. Unlabeled data from an LLM (both truthful and hallucinated) is input. HaloScope identifies a latent subspace representing hallucinated statements. A membership estimation score determines if a data point falls within this subspace. Finally, a binary classifier is trained using this subspace and the membership scores to determine if a given LLM generation is truthful or not.
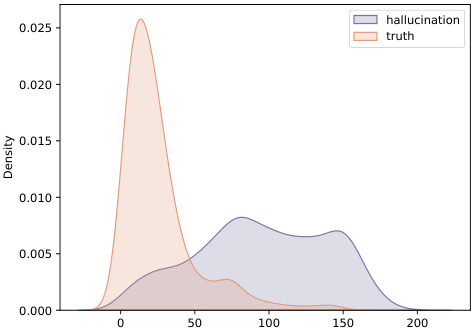
This figure shows the distribution of the membership estimation score for truthful and hallucinated samples in the unlabeled LLM generations of TYDIQA-GP. The score is calculated using LLM representations from the 14th layer of LLaMA-2-chat-7b. The distributions show a reasonable separation between truthful and hallucinated generations, indicating the effectiveness of the score in distinguishing between the two types of data.
More on tables

This table presents the Area Under the ROC Curve (AUROC) scores for various hallucination detection methods on four different datasets: TRUTHFULQA, TRIVIAQA, COQA, and TYDIQA-GP. The methods are compared using two different language models: LLaMA-2 and OPT, each with two different sizes (7B and 13B parameters). The table also indicates whether each method uses single sampling or multiple generations during inference. Higher AUROC values indicate better performance.

This table presents the Area Under the ROC Curve (AUROC) scores for hallucination detection using different embedding locations within the multi-head attention (MHA) architecture of LLMs. It compares performance across two models (LLaMA-2-chat-7b and OPT-6.7b) and two datasets (TRUTHFULQA and TYDIQA-GP). The three embedding locations are: the output of the transformer block (f), the output of the self-attention module (Attn(f)), and the output of the feedforward layer (Q Attn(f)). The results show variation in performance depending on the model and embedding location.

This table presents the results of an ablation study on different design choices for the membership estimation score in the HaloScope model. It compares the performance of three different score designs: a non-weighted score, a score that sums up layer-wise scores, and the HaloScope model’s proposed score (which uses a weighted sum of singular vectors). The results are shown for two different LLMs (LLaMA-2-chat-7b and OPT-6.7b) and two datasets (TRUTHFULQA and TydiQA-GP). The table demonstrates that HaloScope’s proposed score significantly outperforms the other approaches, highlighting the effectiveness of its design choices.
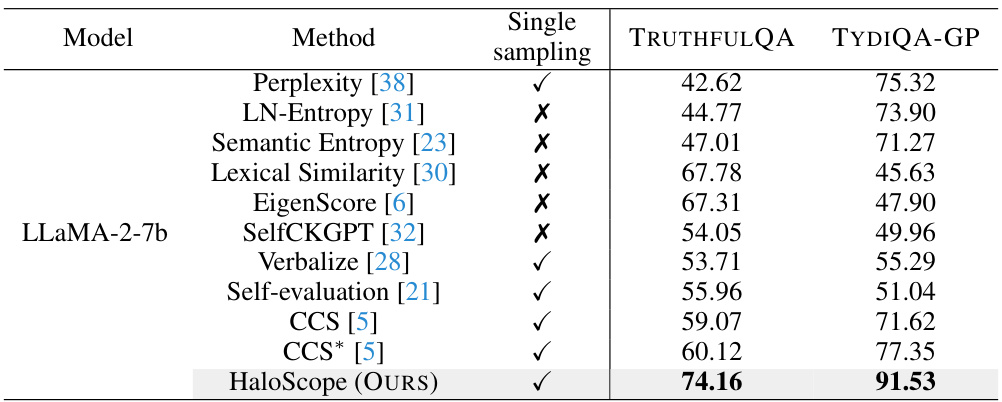
This table compares the performance of HaloScope against several other hallucination detection methods using the Rouge-L metric for evaluating the similarity between generated text and ground truth. It shows the Area Under the ROC Curve (AUROC) scores for each method on two datasets: TRUTHFULQA and TYDIQA-GP. The ‘Single sampling’ column indicates whether a method requires multiple generations during inference. Bold numbers highlight the best performing methods on each dataset.
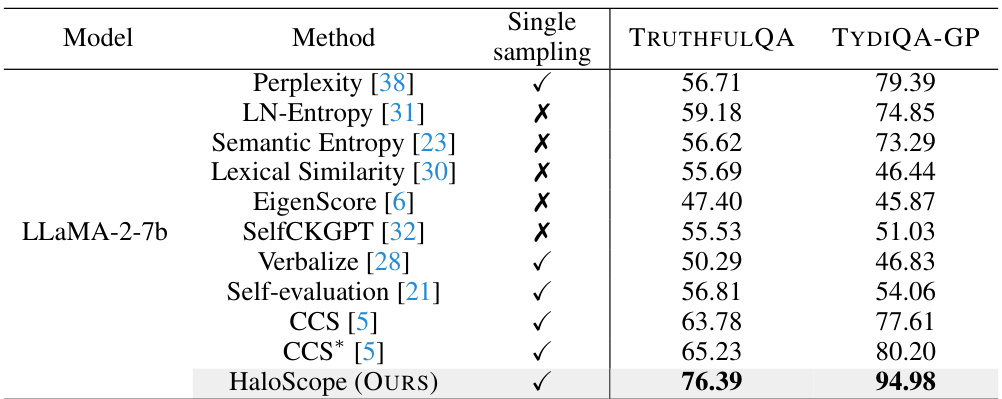
This table presents the results of a hallucination detection experiment using a different random dataset split. It compares HaloScope’s performance against several baseline methods on two datasets, TRUTHFULQA and TYDIQA-GP. The table shows the Area Under the Receiver Operating Characteristic curve (AUROC) for each method, indicating its ability to distinguish between truthful and hallucinated generations. The ‘Single sampling’ column indicates whether each method uses a single generation or multiple generations during testing.

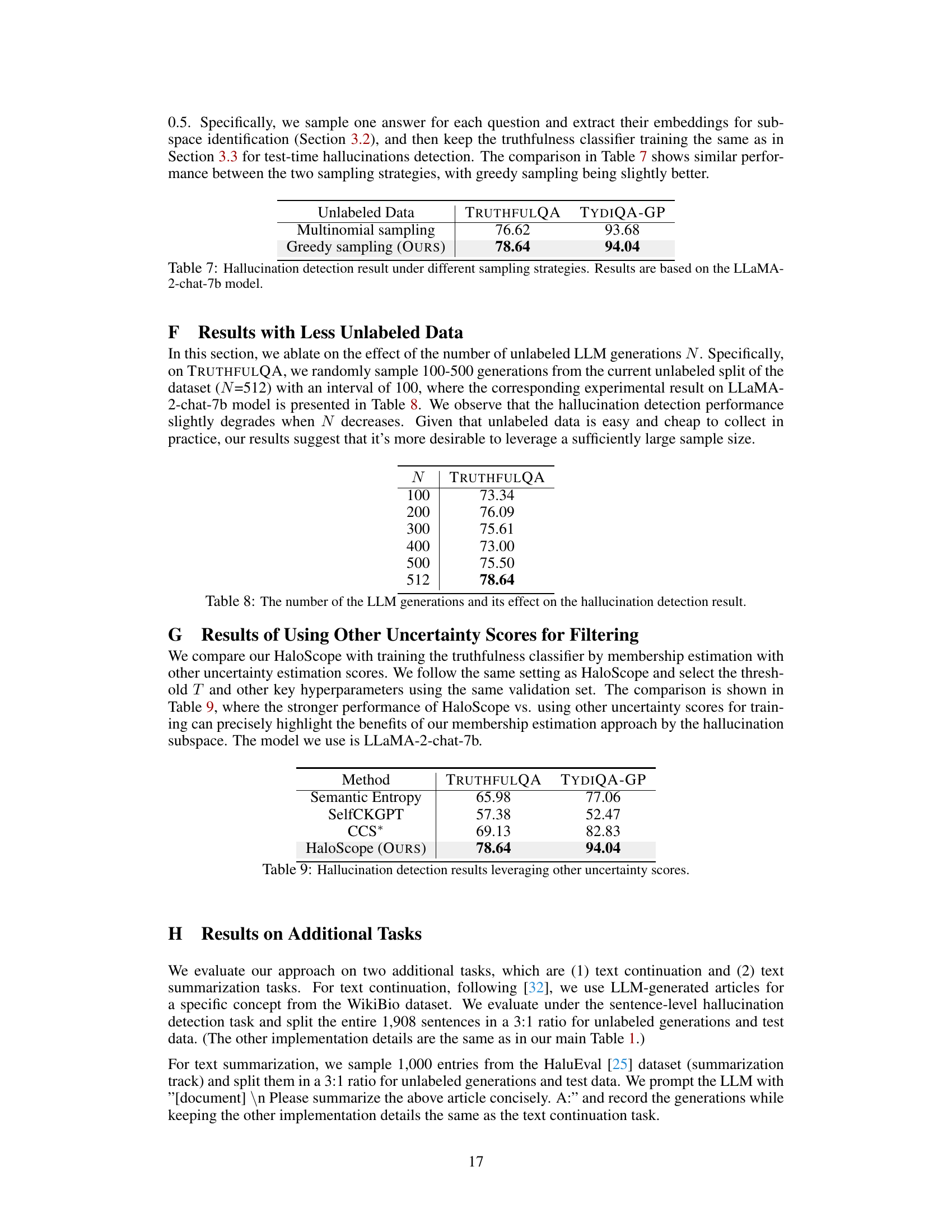
This table presents the results of a study comparing two different sampling methods used for identifying hallucination subspaces in the HaloScope model. The methods are multinomial sampling and greedy sampling (the authors’ approach). The table shows that the greedy sampling method resulted in slightly better performance (higher AUROC scores) for both the TRUTHFULQA and TYDIQA-GP datasets, when using the LLaMA-2-chat-7b model. This suggests that the greedy sampling strategy might be more effective for the subspace identification task within the HaloScope framework.

This table shows the impact of the number of unlabeled LLM generations used for training the hallucination detection model. The AUROC (Area Under the Receiver Operating Characteristic curve) scores for TRUTHFULQA are presented for different sample sizes (N) ranging from 100 to 512. The results indicate that a larger sample size generally leads to improved performance, although the effect is not strictly monotonic.
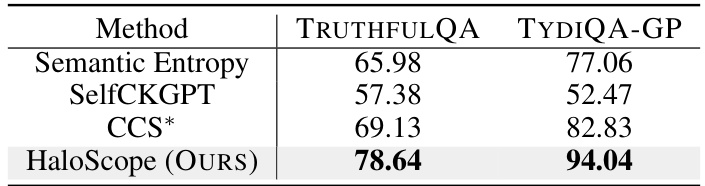
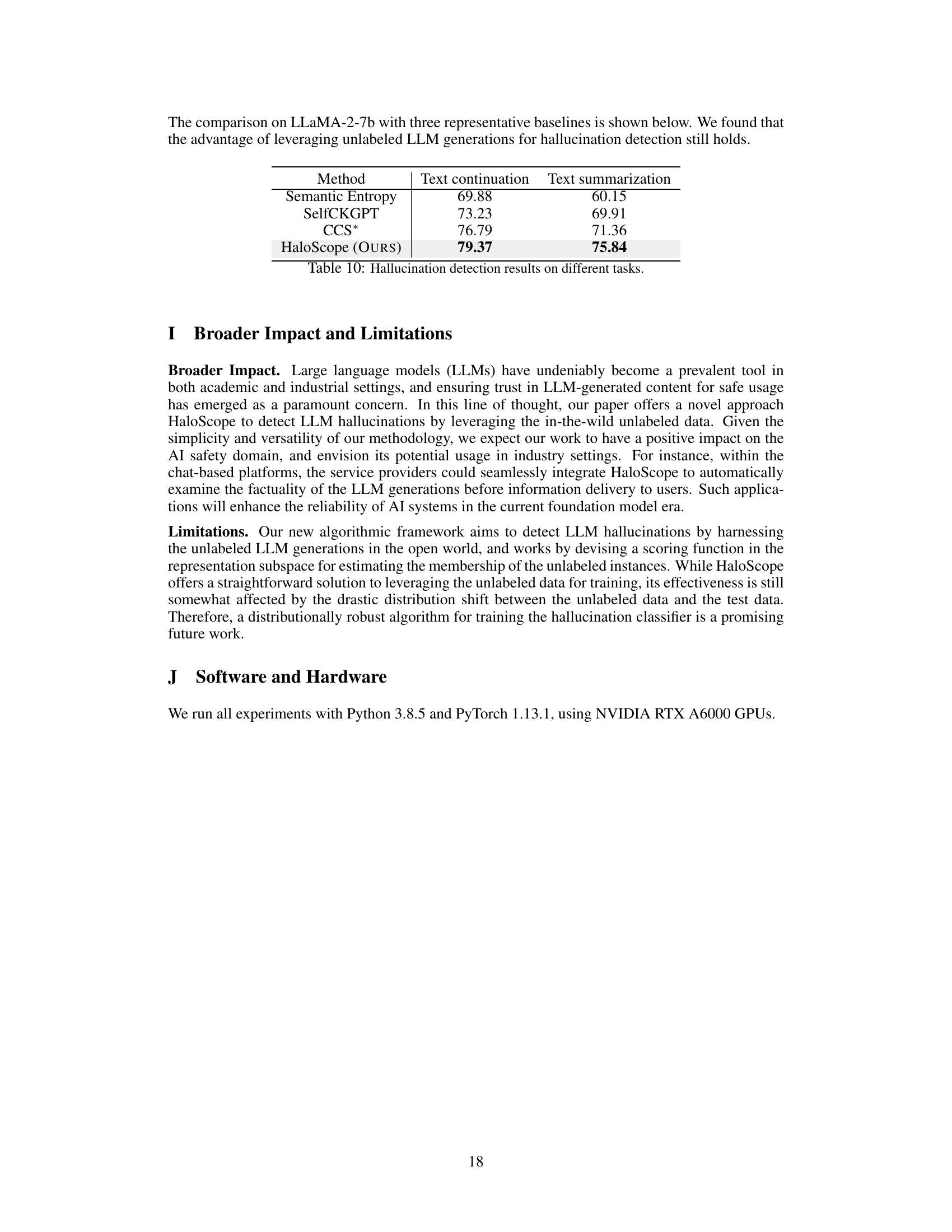
This table compares the performance of HaloScope against other methods using different uncertainty scores for filtering the unlabeled data before training the truthfulness classifier. The results show that HaloScope achieves significantly better performance (higher AUROC) on both the TRUTHFULQA and TYDIQA-GP datasets than the baselines (Semantic Entropy, SelfCKGPT, and CCS*).
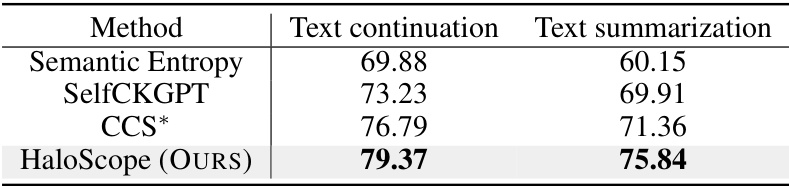
This table presents the performance of HaloScope and baseline methods on two additional tasks: text continuation and text summarization. It shows the area under the ROC curve (AUROC) for each method on each task, demonstrating that HaloScope outperforms the baselines on both tasks. The results highlight the generalizability of HaloScope to various NLG tasks.
Full paper#