↗ OpenReview ↗ NeurIPS Proc. ↗ Hugging Face ↗ Chat
TL;DR#
Large Language Models (LLMs) are increasingly trained on synthetic data, raising concerns about data provenance and potential model theft. Current methods for detecting synthetic data usage, like membership inference attacks, are often unreliable or require prior knowledge of the training data. This paper investigates the ‘radioactivity’ of LLM watermarking—whether traces of watermarked data used to train one LLM can be detected in a subsequently trained LLM. This is a significant challenge as it impacts AI safety, security, and intellectual property.
The researchers developed new radioactivity detection methods to address this issue. These methods, specialized for detecting weak residual watermark signals, reliably detect the presence of watermarked data in fine-tuned models. They found that the detection success is linked to watermark robustness, proportion of watermarked data in training, and the fine-tuning process. Their findings highlight the potential for using watermarking not only to identify AI-generated text, but also to reveal the training data of other models—a crucial development for AI governance and intellectual property protection.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in AI safety and security, intellectual property protection, and large language model development. It introduces a novel method to detect the use of synthetic data in training models, offering significant implications for ensuring data transparency and preventing model theft. The findings open up new research avenues for developing more robust watermarking techniques and improving AI safety protocols.
Visual Insights#

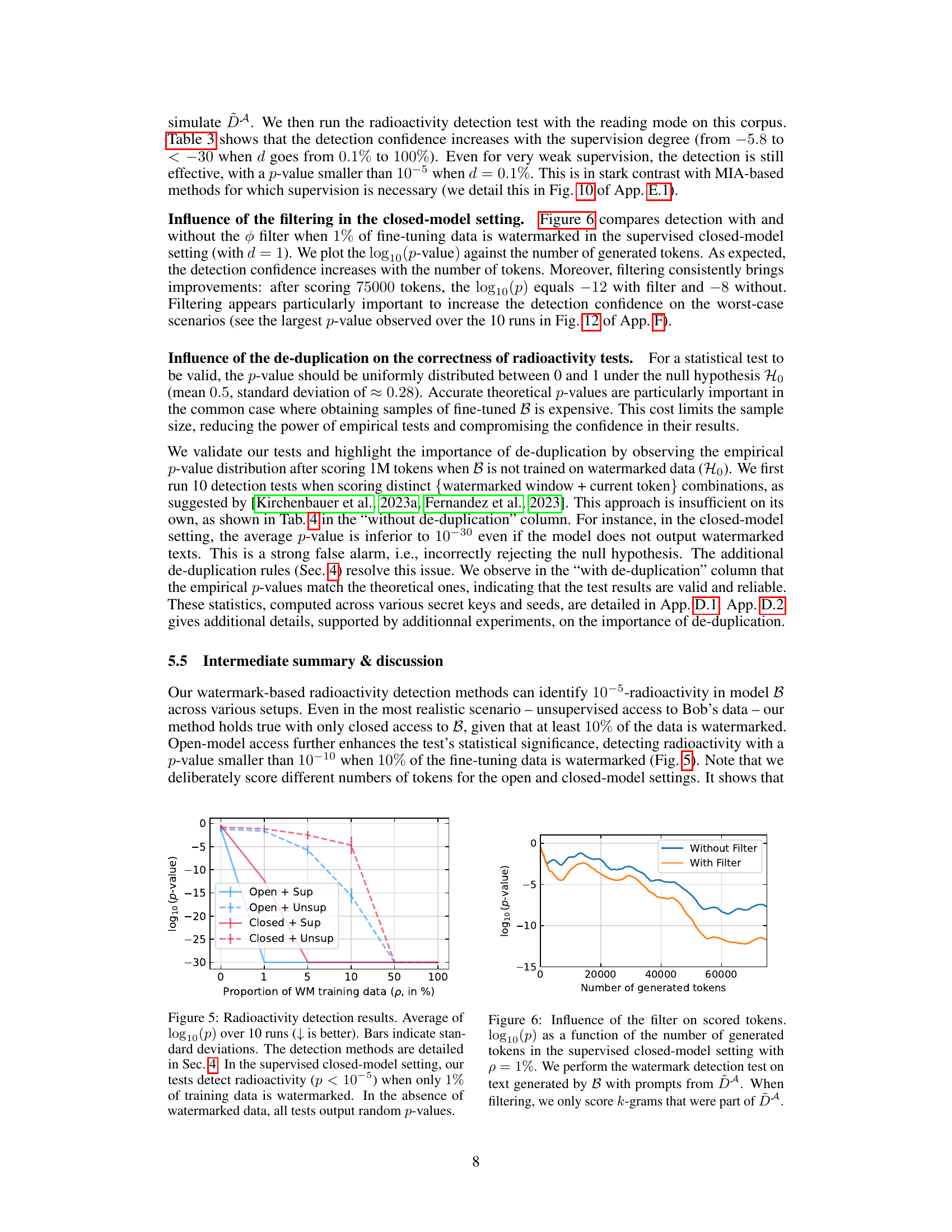
The figure illustrates the concept of ‘radioactivity’ in LLMs. Alice uses a watermarked LLM to generate text. Bob then fine-tunes his own LLM using a dataset that includes some of Alice’s watermarked text. Alice can then detect the presence of her watermarked text in Bob’s fine-tuned LLM by using a statistical test, thus detecting whether Bob trained his model using any of her LLM’s outputs. This demonstrates how watermarked data used in training a model leaves detectable traces in the resulting model.

This table summarizes the availability of radioactivity detection methods under various conditions. It considers whether Alice has access to Bob’s model (open/closed) and the level of supervision Alice has on Bob’s training data (supervised/unsupervised). It also includes the performance of using watermarks versus methods without watermarks (Membership Inference Attacks) and Intellectual Property Protection techniques by Zhao et al. (2023).
In-depth insights#
LLM Radioactivity#
LLM Radioactivity, a novel concept explored in this research paper, refers to the detectable traces left by synthetic data generated by a watermarked Large Language Model (LLM) after it has been used to fine-tune a subsequent LLM. This phenomenon, akin to radioactive contamination, allows researchers to reliably determine if a model’s training dataset included synthetic data from a specific watermarked source. The paper introduces new methods capable of detecting this weak watermark signal with high confidence, even when only a small percentage of the training data is watermarked, pushing beyond the limitations of traditional methods like membership inference. The findings highlight that watermark robustness, the proportion of watermarked data, and the fine-tuning process all significantly affect the detection outcome. Open-source models are particularly susceptible to this detection method. This groundbreaking research has significant implications for intellectual property protection and the transparency of LLM training practices, especially in scenarios where synthetic data is used without clear attribution.
Watermark Detection#
Watermark detection, in the context of large language models (LLMs), is a crucial technique for identifying the origin of generated text. Robust watermarking methods subtly embed identifying signals within the generated text, making them difficult to remove without significantly altering the content. The effectiveness of watermark detection hinges on several factors: the strength of the watermarking algorithm, which determines the resilience of the embedded signal to modifications; the proportion of watermarked data in a model’s training set, impacting the detectability of the signal; and the fine-tuning process, which can either amplify or diminish the watermark’s presence. Open vs. closed-model scenarios present varying challenges in detecting watermarks, with open models enabling direct observation of model outputs for detection, while closed models require indirect analysis of generated text. Statistical testing is vital for determining the significance of detected watermark signals, requiring consideration of factors like the number of tokens analyzed and the probability of false positives. Advanced techniques employ statistical hypothesis testing to provide confidence levels on watermark detection.
Instruction Tuning#
Instruction tuning, a crucial technique in enhancing Large Language Models (LLMs), involves fine-tuning pre-trained LLMs on a dataset of instruction-answer pairs. This process significantly improves the models’ ability to follow diverse instructions and generalize to unseen tasks. The effectiveness of instruction tuning is largely dependent on the quality and diversity of the instruction dataset; high-quality datasets lead to better performance and generalization. Furthermore, the method of instruction generation, whether human-written or synthetically produced, influences the final model’s capabilities. Synthetic data, while cost-effective, may introduce biases or limitations that need to be carefully considered. Finally, the choice of hyperparameters during the fine-tuning process significantly impacts performance, necessitating meticulous tuning and evaluation for optimal results. Therefore, careful dataset curation and parameter optimization are key to successful instruction tuning.
Radioactive Signals#
The concept of “Radioactive Signals” in the context of large language models (LLMs) refers to the detectable traces left behind in a fine-tuned model when it is trained on synthetic data generated by another watermarked LLM. This “radioactivity” signifies that the watermark’s impact, originally intended for detection of AI-generated text, inadvertently reveals the training data’s origin. The strength of these signals is linked to the watermark’s robustness, its proportion in the training dataset, and the fine-tuning process. This novel method provides a more reliable way to detect model imitation than existing techniques, offering provable statistical guarantees even with limited watermarked data in the training set. The research highlights the detection’s reliability by linking contamination levels to specific training factors, therefore presenting a new perspective on data provenance and intellectual property protection within the LLM ecosystem.
Future Research#
Future research directions stemming from this work on LLM watermarking radioactivity could explore several promising avenues. Improving detection robustness across diverse fine-tuning methods and data distributions is crucial. This includes investigating the impact of different watermarking techniques and their interaction with fine-tuning hyperparameters. Developing more sophisticated detection methods that go beyond simple statistical tests is warranted; exploring machine learning based approaches for detecting subtle watermark residuals is a key area. Furthermore, quantifying the relationship between watermark strength and detection accuracy is vital for practical applications. Finally, research into defense mechanisms that can mitigate or eliminate watermark radioactivity is needed, as it directly impacts IP protection and data privacy. This could involve developing novel fine-tuning strategies or exploring data augmentation techniques.
More visual insights#
More on figures

This figure illustrates the core concept of the paper: Alice’s watermarked LLM outputs are used as part of Bob’s training data for his LLM. Even though the proportion of watermarked data is small, the watermark leaves detectable traces in Bob’s model, allowing Alice to reliably determine whether Bob trained his model using her data. This demonstrates the ‘radioactivity’ of LLMs.
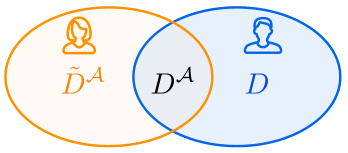
This figure is a Venn diagram showing the relationship between three sets of data: D, ĎA, and DA. D represents the entire dataset used by Bob to fine-tune his language model. ĎA represents the set of all outputs generated by Alice’s language model. DA represents the intersection of D and ĎA – the portion of Bob’s training data that originated from Alice’s model. The diagram visually explains that the detection performance (radioactivity) primarily depends on two factors: (1) p, which represents the proportion of Bob’s training data derived from Alice’s model; and (2) d, which represents the degree of supervision or the extent to which Alice knows Bob’s training data.
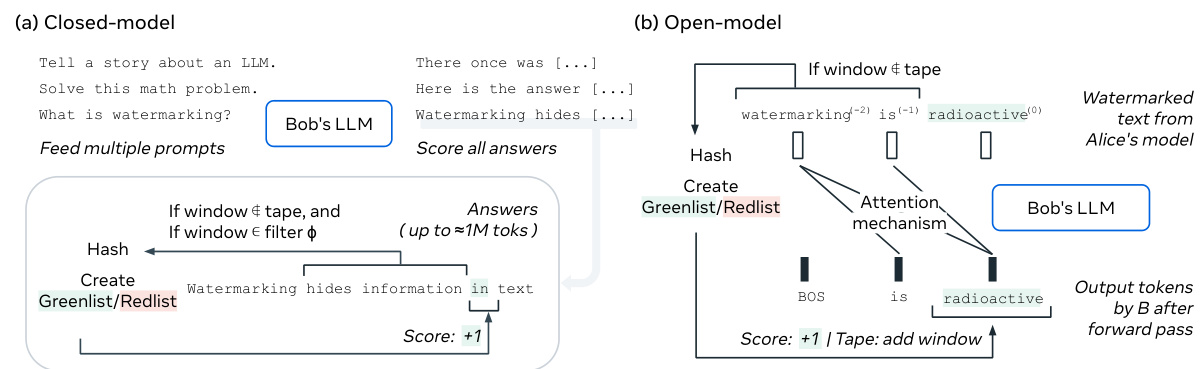
This figure illustrates the concept of ‘radioactivity’ in LLMs. Alice fine-tunes her language model (LLM) with watermarked text. Bob then fine-tunes his own LLM using a dataset that includes some of Alice’s watermarked outputs. Alice can then use her watermark detection method to detect traces of her original watermarked data in Bob’s fine-tuned model, even though Bob may not have intentionally included her data and is unaware of the watermark. This demonstrates the ‘radioactive’ nature of the watermarked data, leaving detectable traces in models trained on it.

This figure illustrates the concept of ‘radioactivity’ in LLMs. Alice’s LLM generates watermarked text. Bob then fine-tunes his LLM using a dataset that includes some of Alice’s watermarked text. Alice can then detect the presence of her watermarked text in Bob’s fine-tuned model, even if only a small portion of Bob’s training data came from her model. This demonstrates that the watermark leaves detectable traces in models trained on the watermarked data, revealing information about the training data used.
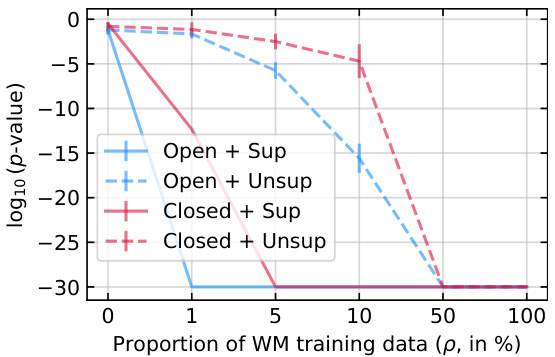
This figure shows the results of radioactivity detection experiments under various conditions. The x-axis represents the percentage of watermarked training data used in fine-tuning model B. The y-axis shows the average base-10 logarithm of the p-value obtained from the statistical test for radioactivity. Lower values indicate stronger evidence of radioactivity. The results are shown separately for four scenarios: open model with supervision, open model without supervision, closed model with supervision, and closed model without supervision. The error bars represent the standard deviations across 10 runs of the experiment. The figure demonstrates that even a small percentage of watermarked data can lead to detectable radioactivity, particularly in open-model settings. When no watermarked data is used, the p-values are randomly distributed around 0.
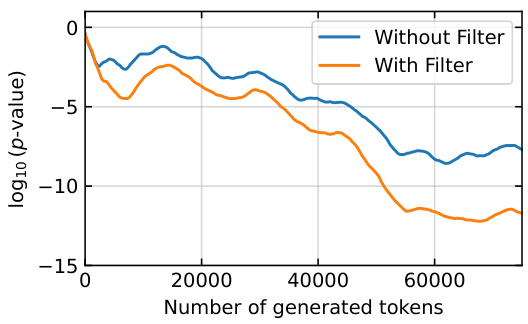
This figure shows the impact of using a filter on the performance of the radioactivity detection test. The test is performed in a closed-model setting where only 1% of the training data is watermarked. The x-axis represents the number of tokens generated by model B, and the y-axis shows the log10 of the p-value. Two lines are plotted: one for the test without a filter and one with a filter. The filtered test shows a significantly lower p-value (stronger evidence of radioactivity) for the same number of generated tokens.
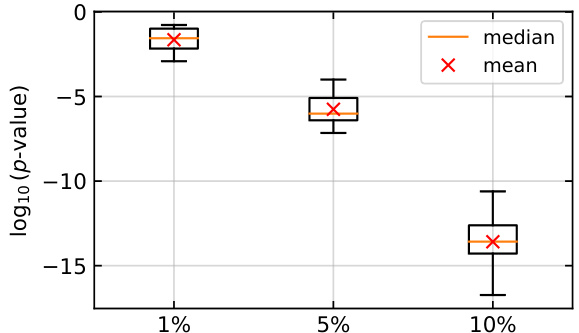
This box plot visualizes the distribution of log10(p-values) obtained from the radioactivity detection test in the open-model and unsupervised setting. The x-axis represents different proportions (p) of watermarked data used for fine-tuning model B, while the y-axis shows the log10(p-value). Each box represents the interquartile range (IQR), the median is marked by the orange line, and the mean is marked by the red cross. The whiskers extend to the maximum and minimum values, excluding outliers. The plot demonstrates how the distribution of p-values shifts toward stronger evidence of radioactivity (lower p-values) as the proportion of watermarked data increases.
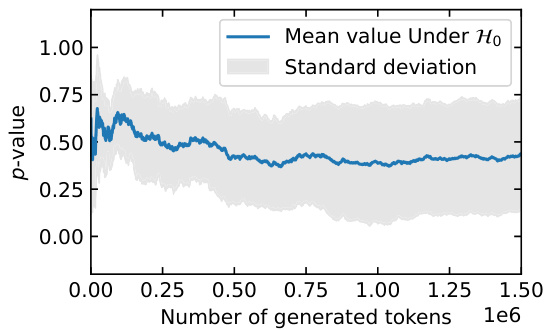
This figure shows the results of the radioactivity detection test in the open/unsupervised setting. The y-axis represents the log10(p-value), and the x-axis represents the proportion of watermarked training data (p). The box plot shows the distribution of log10(p-values) across multiple runs. The mean log10(p-value) is shown as a solid line, and the standard deviation is represented by a shaded area. For each proportion of watermarked data, ten runs of the experiment were performed, and these results are displayed as box plots.
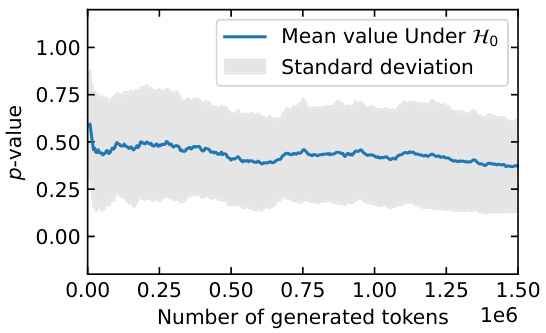
This figure shows the distribution of p-values obtained from the radioactivity detection test in an open-model, unsupervised setting, across various proportions (p) of watermarked data used in fine-tuning model B. The box plots illustrate the median, mean, and standard deviation of the log10(p) values. It visually represents the data presented in Figure 5, where only the mean values were shown.
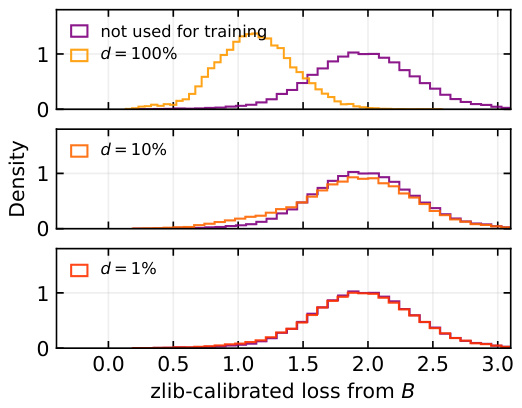
This figure compares the performance of membership inference attacks (MIA) and watermarking-based methods for detecting radioactivity in a language model. The left panel shows the distributions of calibrated loss from model B (the suspect model) for data that was and wasn’t used in training. The difference in distributions becomes less pronounced as the degree of supervision (d) decreases, indicating that MIA becomes less effective with less overlap between training and test data. The right panel illustrates that the watermarking method consistently achieves high detection confidence (p-value < 10^-5) even with low supervision (d < 2%), demonstrating its superior performance compared to MIA in detecting model imitation.
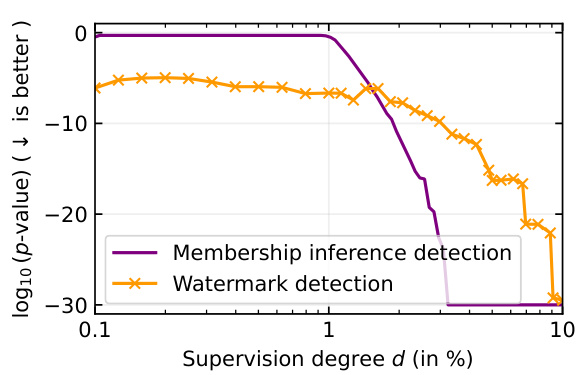
This figure compares two methods for detecting model imitation: Membership Inference Attacks (MIA) and watermark detection. The left panel shows the distribution of perplexity scores for models trained with and without data from a source model. The difference in distributions is used to detect imitation. However, the effectiveness of MIA diminishes as the proportion of imitated data decreases (low supervision). The right panel shows that watermark detection remains effective even at low supervision levels, providing more reliable detection of model imitation.
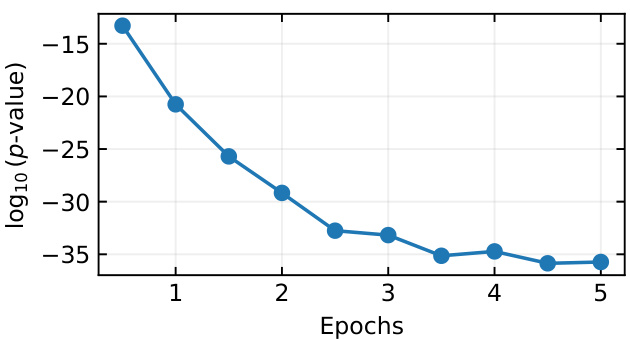
This figure shows how the number of epochs during the fine-tuning process affects the detection of watermarks. As the number of epochs increases, the watermark becomes more prominent, leading to a stronger detection signal (lower p-value).
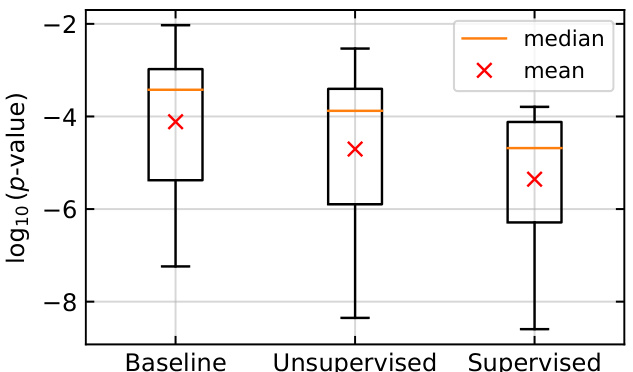
This figure shows box plots illustrating the impact of using a filter on the log10(p)-values obtained from a radioactivity detection test in a closed-model setting, where only 10% of the fine-tuning data was watermarked. Three scenarios are compared: a baseline without filtering, an unsupervised setting where the filter is constructed from newly generated watermarked data, and a supervised setting where the filter is built using the known watermarked data from the training set (DA). The plots display the median and mean log10(p)-values for each scenario, providing a visual representation of how the filtering method enhances the accuracy of radioactivity detection by focusing the analysis on specific k-grams.
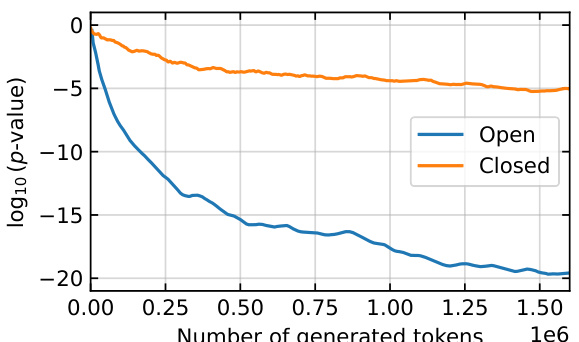
This figure shows how the p-value (a measure of statistical significance) changes as more tokens are scored in a closed-model setting where only 1% of the training data was watermarked. The x-axis shows the number of generated tokens, and the y-axis represents the log10 of the p-value. Two lines are displayed, one for when a filter is used and one without. The filter helps focus the analysis on specific tokens, making it easier to detect the watermark even with a small amount of watermarked data in the training set. A smaller p-value indicates stronger evidence that the model was indeed trained on watermarked data.
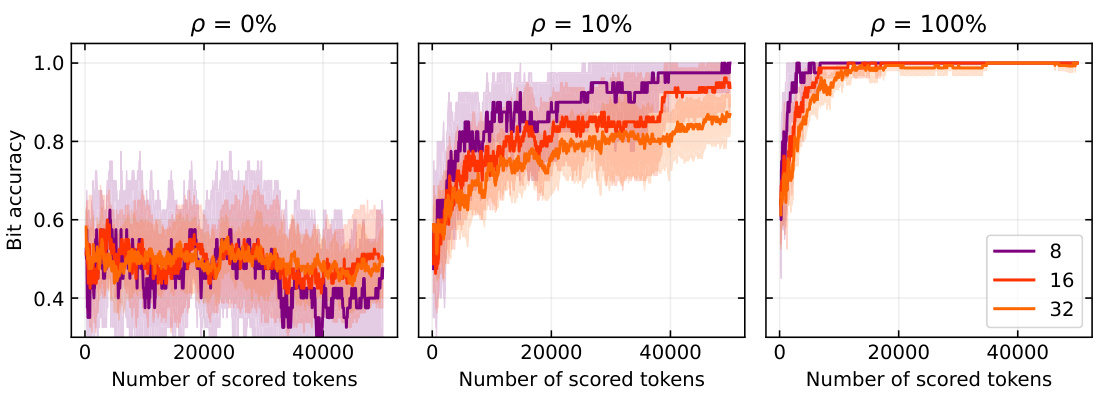
This figure shows the bit accuracy of watermark extraction using the MPAC method under different conditions. The x-axis represents the number of scored tokens, and the y-axis represents the bit accuracy. There are three plots, one for each proportion (p) of watermarked data used in fine-tuning: 0%, 10%, and 100%. Each plot shows curves for different message lengths (8, 16, and 32 bits). The results indicate that bit accuracy increases with the number of scored tokens and the proportion of watermarked data, but decreases with message length. This suggests that even multi-bit watermarking schemes exhibit radioactivity.
More on tables
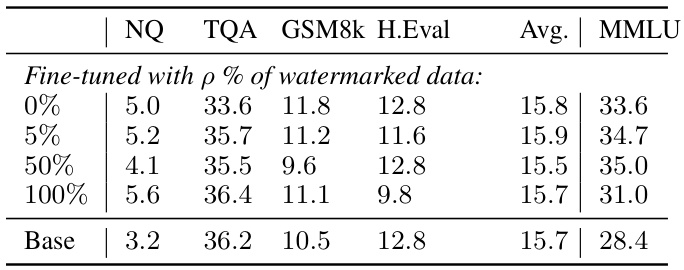
This table presents the results of evaluating the Llama-7B language model after fine-tuning it with varying percentages of watermarked instruction data. The evaluation is performed across several benchmark datasets (NQ, TQA, GSM8k, H.Eval, MMLU) to assess the model’s performance in different tasks. The ‘Base’ row shows the baseline performance of the model without any watermarked data in its training. This allows for a comparison of performance with and without watermarked data at various proportions (5%, 50%, and 100%).

This table presents the detection confidence (log10(p-value)) results for detecting radioactivity in the open-model setting. The detection is performed using the ‘reading mode’ described in the paper. It shows how the detection confidence changes with varying degrees of supervision (d), while maintaining a constant proportion (p=5%) of Bob’s training data originating from Alice’s model (A). Lower log10(p) values indicate stronger evidence of radioactivity.
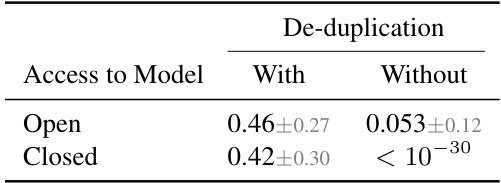
This table presents the results of a statistical test evaluating the correctness of the radioactivity detection methods. It demonstrates the importance of de-duplication in ensuring reliable p-values. The results show that without de-duplication, the p-values are significantly lower than expected (0.5), indicating that the test is not working correctly, while with de-duplication the p-values are closer to the expected value.

This table presents the average log10 p-values for watermark detection and radioactivity detection using two different watermarking methods (KGW and AK) with varying watermark window sizes (k=1, 2, 4). The ‘Orig’ values represent the results of watermark detection on the original watermarked training texts, while ‘Rad’ represents the results of radioactivity detection on a model fine-tuned with watermarked data. The results show that lower k values (smaller watermark windows) generally lead to higher radioactivity, indicating stronger contamination of the model by watermarked data.
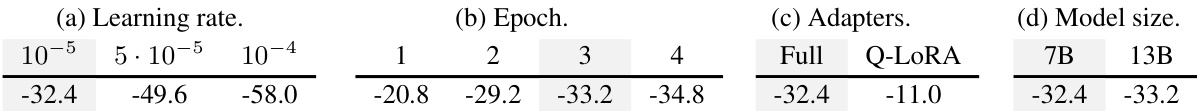
This table shows the impact of different hyperparameters during the fine-tuning process on the radioactivity of the model. It presents the log10(p-value) for a statistical test of radioactivity, where a lower p-value indicates stronger radioactivity. The hyperparameters considered are the learning rate, the number of epochs, the type of adapters used (full or Q-LoRA), and the size of the language model (7B or 13B). The values used in Section 5 of the paper are highlighted in gray.
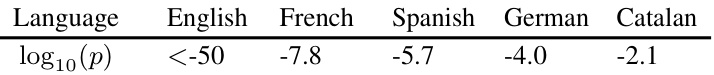
This table presents the results of a radioactivity detection test conducted on different languages. The test involved prompting model B with the beginnings of Wikipedia articles in various languages and then performing detection on the generated next tokens using the closed-model setting from Section 4 of the paper. The results show the log10(p) values for each language, indicating the confidence level of the detection test.
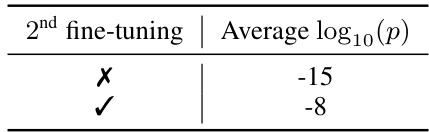
This table shows the results of an experiment to evaluate if a second fine-tuning on non-watermarked data can remove the watermark traces from a model that was previously fine-tuned with watermarked data. The experiment shows that a second fine-tuning reduces the radioactivity (strength of the watermark signal) but does not completely remove it.

This table shows the p-values obtained from applying the watermark detection test on non-watermarked instruction-answer pairs generated by Llama-2-chat-7B. The p-values are shown for different lengths of text (number of lines and number of characters). As the length of the text increases, the p-values become increasingly smaller, indicating stronger evidence against the null hypothesis (no watermark).

This table presents summary statistics (mean and standard deviation) of the base-10 logarithm of the p-value (log10(p)) obtained from watermark detection tests. The tests were performed on different text lengths (ranges of token numbers), all generated using the Llama-2-chat-7B model and a specific watermarking technique (Kirchenbauer et al., 2023b) with parameters δ = 3.0, γ = 0.25, and k = 2 (as described in Section 5 of the paper). Each range of token counts contains roughly 500 texts, and the table shows the average log10(p) and its standard deviation for each length range.
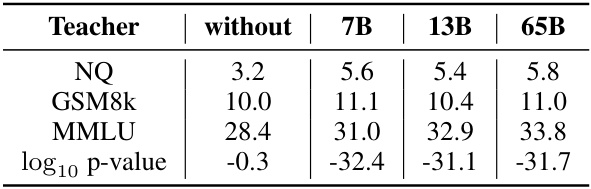
This table presents the results of experiments using different sizes of Llama-2-chat models as teachers for fine-tuning a Llama-1-7B model. The ‘Teacher’ column indicates the size of the Llama-2-chat model used. The subsequent columns show the performance on several benchmarks (NQ, GSM8k, MMLU) and the log10(p-value) for radioactivity detection. The results demonstrate that larger teacher models yield better results on the benchmarks and similar levels of radioactivity detection.

This table shows the results of an experiment where the fine-tuning process was done with 10% of watermarked data mixed with either human-generated or machine-generated instructions. The results demonstrate that mixing watermarked data with human-generated instructions leads to stronger radioactivity signals compared to mixing with machine-generated instructions. The average log10(p) value is significantly lower for the data mixed with human instructions indicating greater detection confidence.

This table presents the results of radioactivity detection experiments conducted using a closed-model setting. It compares the detection performance (measured by the average and maximum log10(p-value) across 10 runs) with and without applying a filter on the scored k-grams. The filter’s impact on improving detection accuracy is highlighted, particularly in scenarios with less reliable results.
Full paper#