↗ OpenReview ↗ NeurIPS Proc. ↗ Chat
TL;DR#
Large Language Models (LLMs) are prone to generating unreliable outputs, including hallucinations and factual errors. This unreliability hinders the deployment of LLMs in high-stakes applications. Current mitigation strategies often involve using reward models or human feedback to steer the model, but these methods can be resource-intensive and may not always be effective.
This paper proposes a communication-theoretic approach to address this issue. It views the LLM generation process as a noisy communication channel and suggests using redundancy – generating multiple outputs and reranking them – to improve reliability. The authors show theoretically and empirically that this strategy effectively reduces error rates, even when the reranker is not perfect. The work contributes new theoretical insights and practical guidelines for LLM developers and researchers, particularly in optimizing reranking strategies for enhanced LLM safety and performance.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working with large language models (LLMs) because it introduces a novel communication-theoretic framework for analyzing and improving LLM reliability. The framework offers a powerful new way to understand and mitigate the issue of hallucinations and errors in LLMs, opening new avenues for research in error correction, reranking strategies, and overall LLM safety. It also provides empirically validated reranking laws, which are directly applicable in various LLM applications.
Visual Insights#
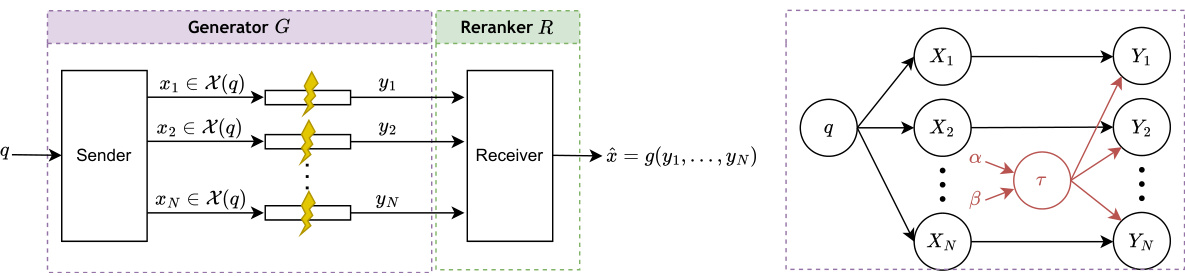
The figure illustrates the generator-reranker system as a communication system. The left panel shows a query q being processed by a generator G, producing N hypotheses that are sent through noisy channels to a reranker R. The reranker then produces the final output. The right panel provides graphical models for the generator G, showing both scenarios with independent and exchangeable hypotheses.
In-depth insights#
Redundancy in LLMs#
The concept of “Redundancy in LLMs” explores the deliberate introduction of multiple, potentially similar, outputs from a large language model (LLM) during the generation process. This strategy, inspired by communication theory’s error correction techniques, aims to improve LLM reliability. Redundancy acts as a form of built-in error detection, as the presence of several answers allows for comparison and identification of superior, less hallucinatory responses. A reranker algorithm is crucial here, choosing the most suitable from the redundant set. This approach is particularly valuable for mitigating LLMs’ tendency to produce hallucinated or nonsensical results, particularly in high-stakes situations. Mallows and Zipf-Mandelbrot models are often used to mathematically understand reranker behavior and the decay of error probability with increased redundancy. While introducing redundancy adds computational complexity, the asymptotic error-free nature demonstrated in theoretical analyses highlights the potential for this method to significantly enhance LLM performance and safety. The trade-off between computation and enhanced reliability forms a critical aspect of this field, prompting further investigation into optimized redundancy strategies.
Reranker Imperfection#
The concept of ‘reranker imperfection’ is crucial in evaluating the robustness and reliability of language models that employ a reranking strategy. A perfect reranker, while theoretically useful, is unrealistic. Real-world rerankers are imperfect, meaning their ranking decisions are not always optimal and can be influenced by noise or biases present in the data or model. Understanding and modeling this imperfection is key to developing more accurate and reliable reranking systems. The paper likely explores different models to characterize reranker imperfection, such as the Mallows or Zipf-Mandelbrot models, examining how these imperfections impact the overall system performance. The analysis likely probes the rate of convergence towards acceptable answers, demonstrating how much redundancy (i.e., the number of hypotheses generated) is necessary to mitigate the effects of an imperfect reranker. This could lead to the derivation of ‘reranking laws,’ mathematical relationships providing practical guidelines for balancing the trade-off between generation cost and performance given a reranker’s level of imperfection. Incorporating realistic models of reranker imperfection allows for a more nuanced and practical assessment of the effectiveness of reranking methods. This detailed analysis is important for building more dependable and trustworthy LLMs, highlighting the significance of considering the inherent limitations of the chosen reranking technique.
Dependent Channels#
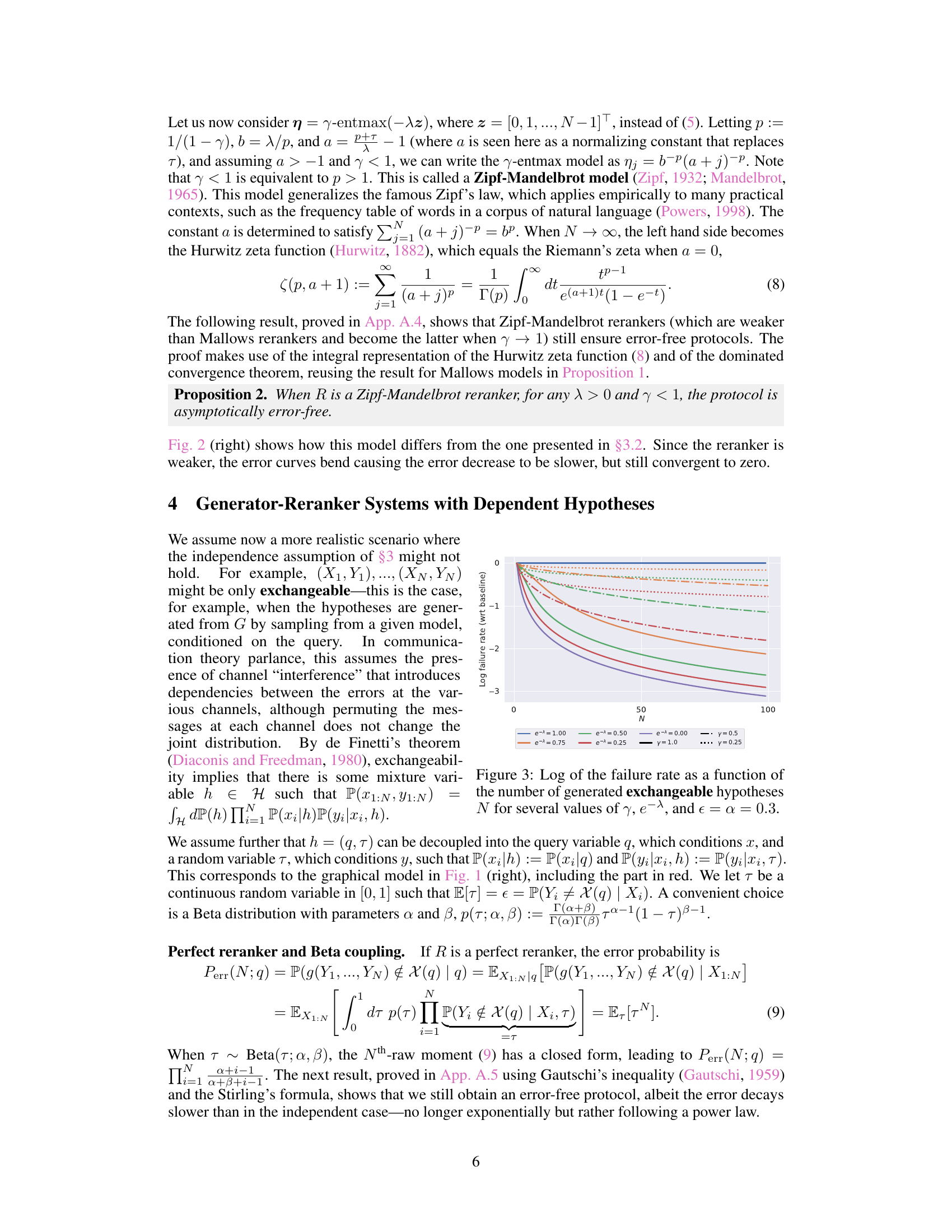
The concept of ‘Dependent Channels’ in the context of a large language model (LLM) reranking system introduces a more realistic communication model compared to the independent channel assumption. In an LLM, the generated hypotheses are unlikely to be truly independent; they share a common origin (the LLM) and might exhibit statistical dependencies. Modeling these dependencies through ‘Dependent Channels’ is crucial because it directly impacts the effectiveness of reranking. Independent channels assume that errors in individual hypotheses are isolated, making it easier to recover the correct answer by selecting the most reliable. However, with dependence, errors can be correlated; if one hypothesis is wrong, others generated in the same context might also be wrong. This means the reranker’s job gets significantly harder. To address this complexity, the framework may involve Bayesian modeling, where a latent variable (e.g., reflecting the model’s internal state or a latent topic) influences the noise affecting multiple channels. Analyzing this dependence is key to deriving accurate reranking laws, predicting how quickly error probability decays with the number of generated hypotheses, and designing better reranking strategies that account for the inherent correlations in LLM outputs.
Empirical Validation#
An empirical validation section in a research paper would rigorously test the study’s claims. It would involve designing experiments that directly address the paper’s hypotheses, using appropriate datasets and metrics. Careful consideration of experimental design is crucial, including aspects like sample size, randomization, and control groups, to ensure the validity of the results. The section should clearly describe the methodologies employed, providing sufficient detail for reproducibility. Statistical analysis of the results is essential to determine if the observed effects are significant and to quantify the strength of the relationships. Visualizations, such as graphs and charts, should effectively convey the key findings. Transparency regarding limitations of the experimental setup and potential biases is important for maintaining scientific rigor. A robust empirical validation provides strong evidence supporting the theoretical findings, lending credibility and impact to the overall research.
Future Directions#
Future research could explore extending the theoretical framework to handle continuous quality metrics instead of binary classifications, enabling a more nuanced analysis of LLM performance. Investigating the impact of different reranker models and their associated parameters on the asymptotic error rate would also be valuable. Additionally, the current analysis assumes a perfect or imperfect reranker, but real-world rerankers often lie somewhere in between. A more realistic model capturing this spectrum would improve the practical applicability of the findings. Exploring the effects of various dependency structures between hypotheses could refine the theoretical bounds and offer further insights into the behavior of the proposed protocol in more realistic LLM scenarios. Finally, empirical validation across a broader range of LLMs and tasks, including those with different architectural designs and training procedures, would enhance the generalizability and robustness of the results. The exploration of these directions promises to yield a more comprehensive and practical understanding of the effectiveness of generator-reranker systems for enhancing the safety and reliability of LLMs.
More visual insights#
More on figures
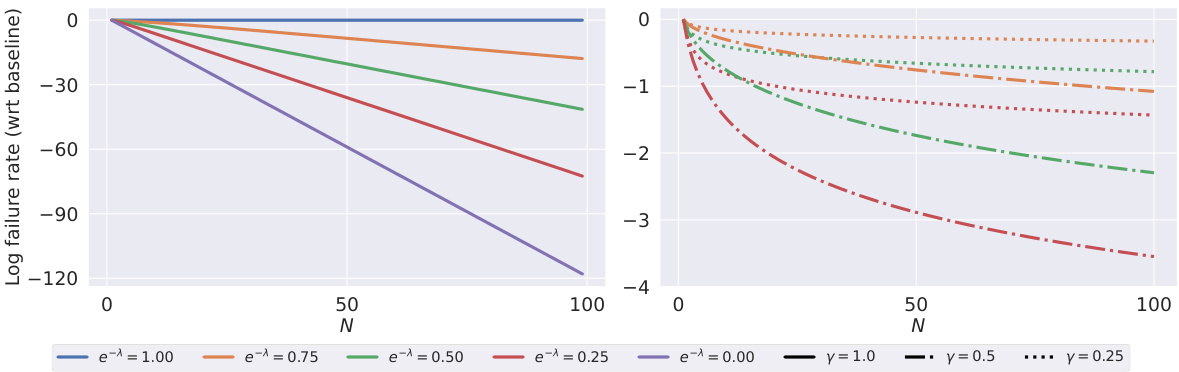
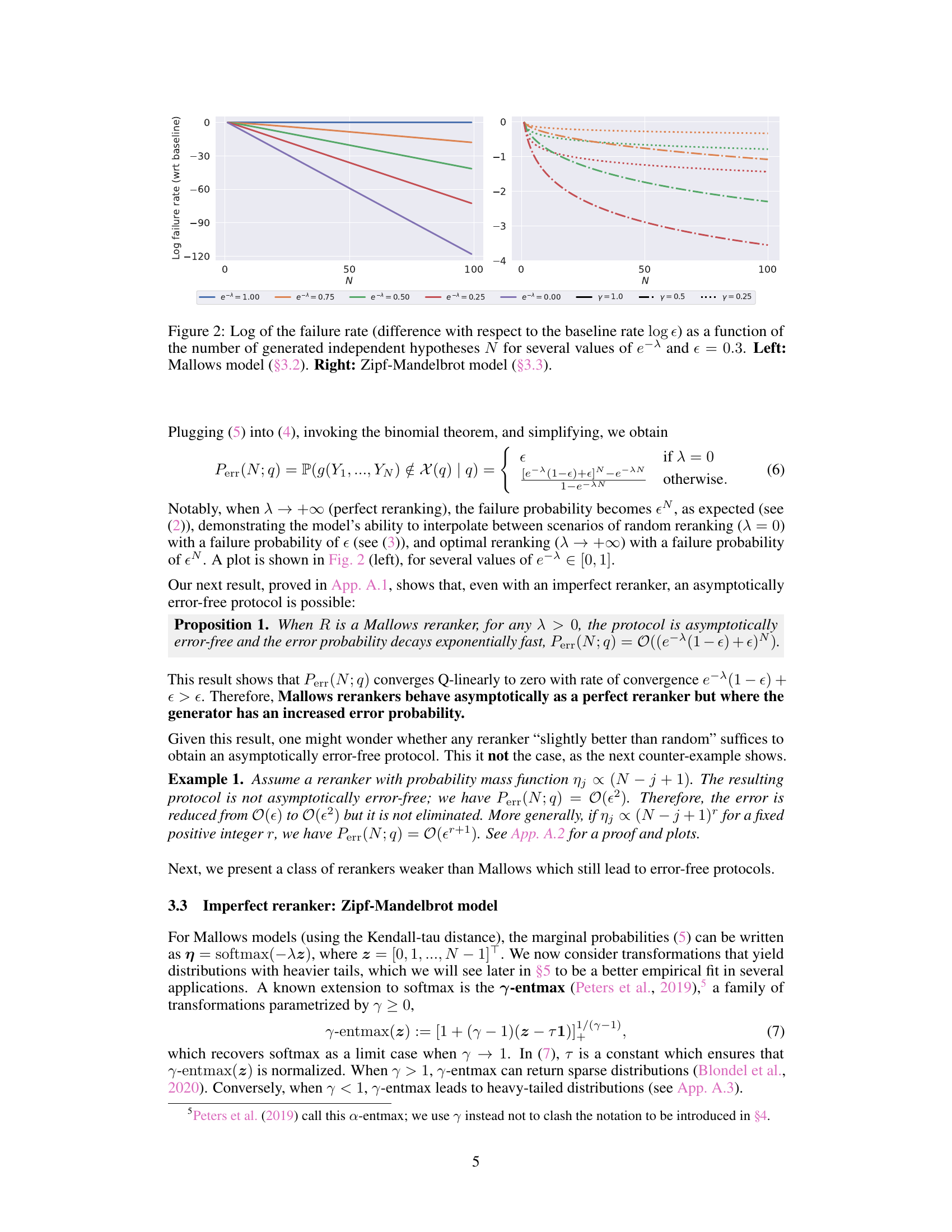
This figure displays the relationship between the number of generated hypotheses (N) and the failure rate (compared to the baseline rate) for two different reranker models: Mallows and Zipf-Mandelbrot. It shows how the failure rate decreases as the number of hypotheses increases, and how this decrease is affected by different parameters of the reranker models (lambda (λ) for Mallows and gamma (γ) for Zipf-Mandelbrot). The left panel shows the results for the Mallows model, demonstrating an exponential decrease in the failure rate. The right panel shows the results for the Zipf-Mandelbrot model, indicating a slower decrease, following a power-law decay.
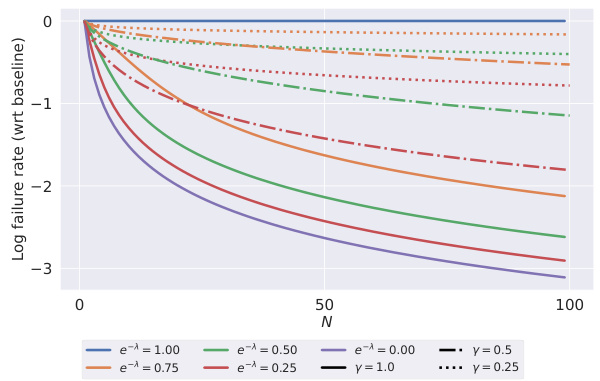
This figure shows the log of the failure rate, relative to the baseline failure rate (log ε), as a function of the number of generated hypotheses (N). Separate plots are shown for both Mallows and Zipf-Mandelbrot reranker models, demonstrating how the failure rate decreases with increasing N under different reranker parameters (λ for Mallows and γ for Zipf-Mandelbrot). The plots illustrate the different rates of convergence for the two models, highlighting the asymptotic error-free nature of both.
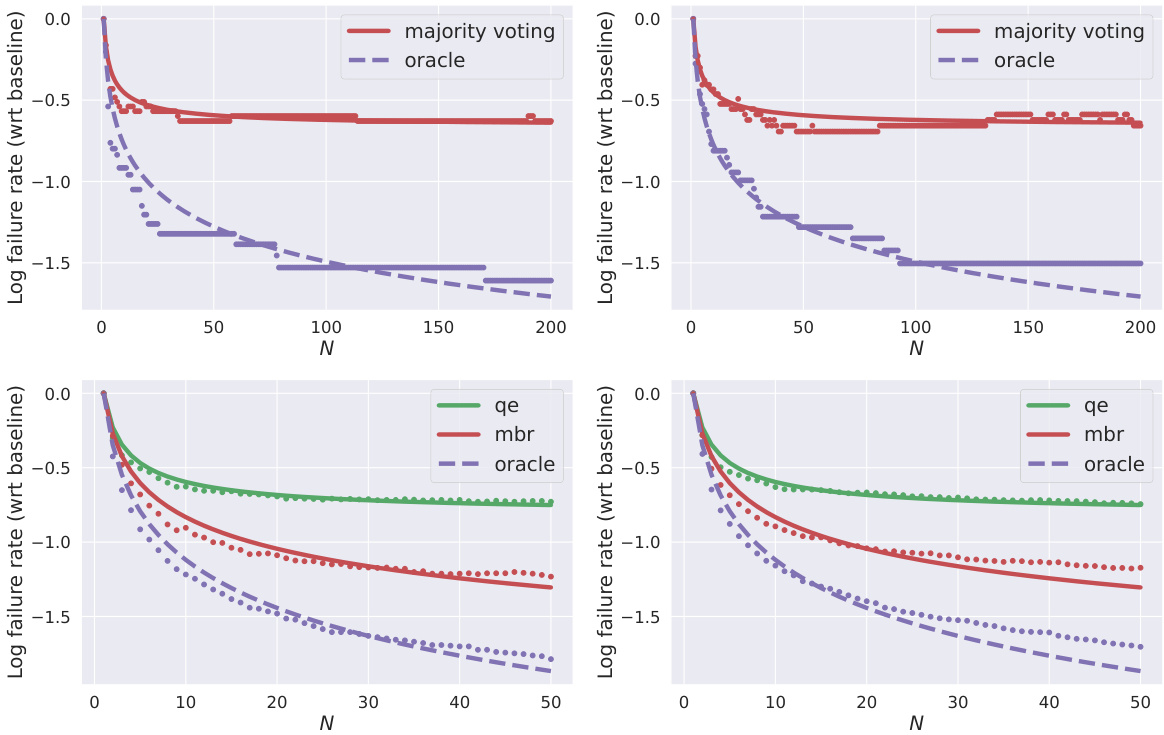
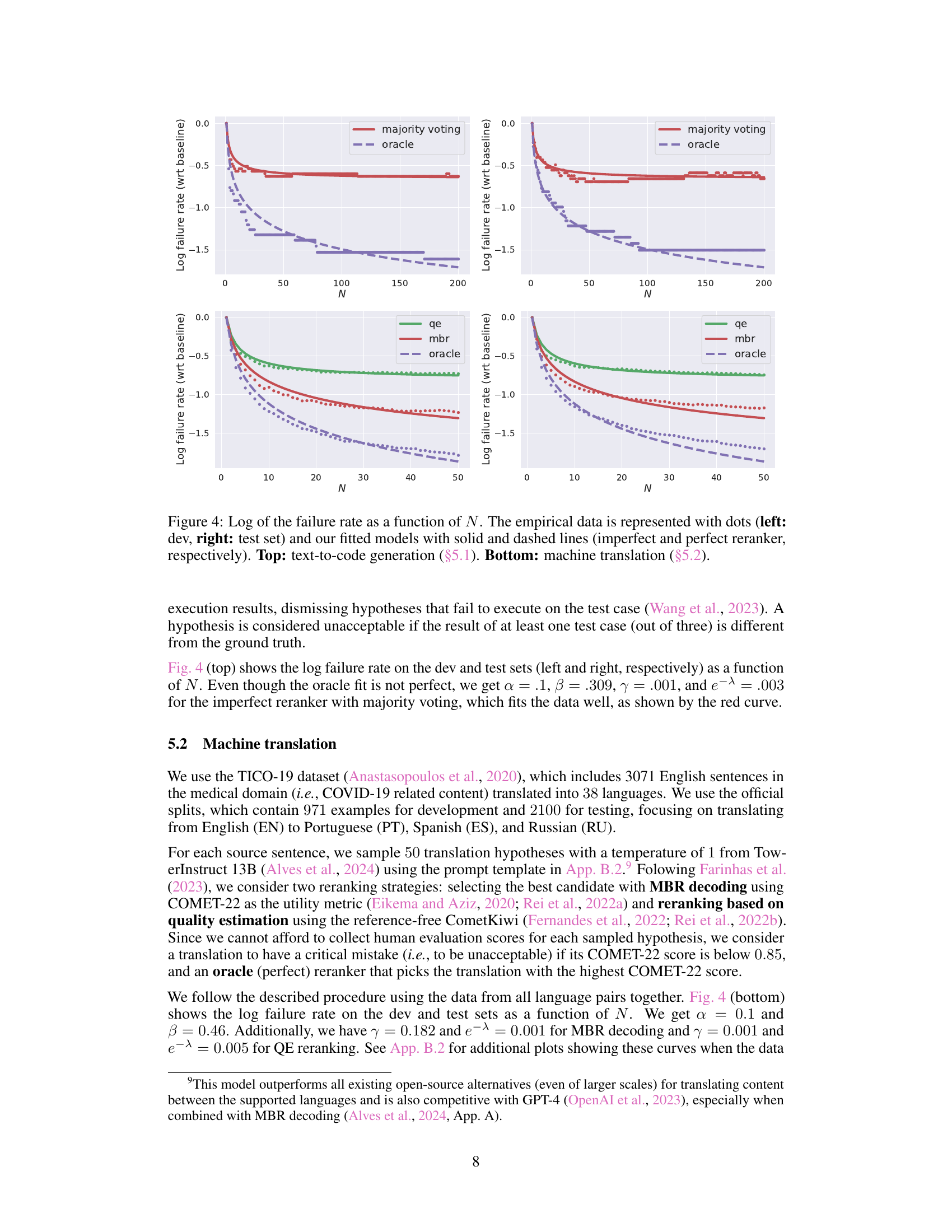
This figure shows the results of the experiments on two tasks: text-to-code generation and machine translation. The x-axis represents the number of hypotheses (N) generated by the language model. The y-axis represents the log of the failure rate (compared to a baseline). The plots show that the failure rate decreases as the number of hypotheses increases. The figure shows empirical data points and fitted models that confirm the reranking laws of the paper. Separate plots are given for the development and test sets for both tasks.
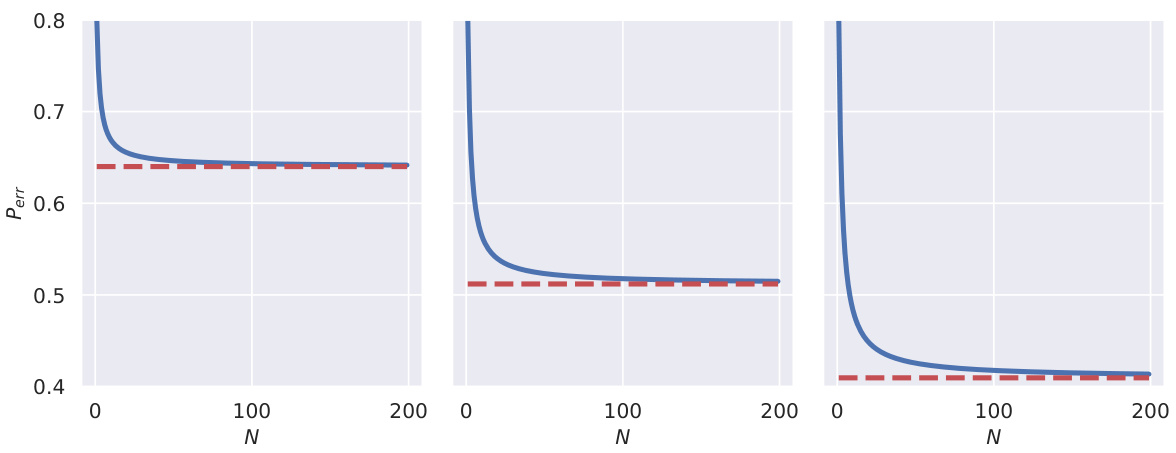
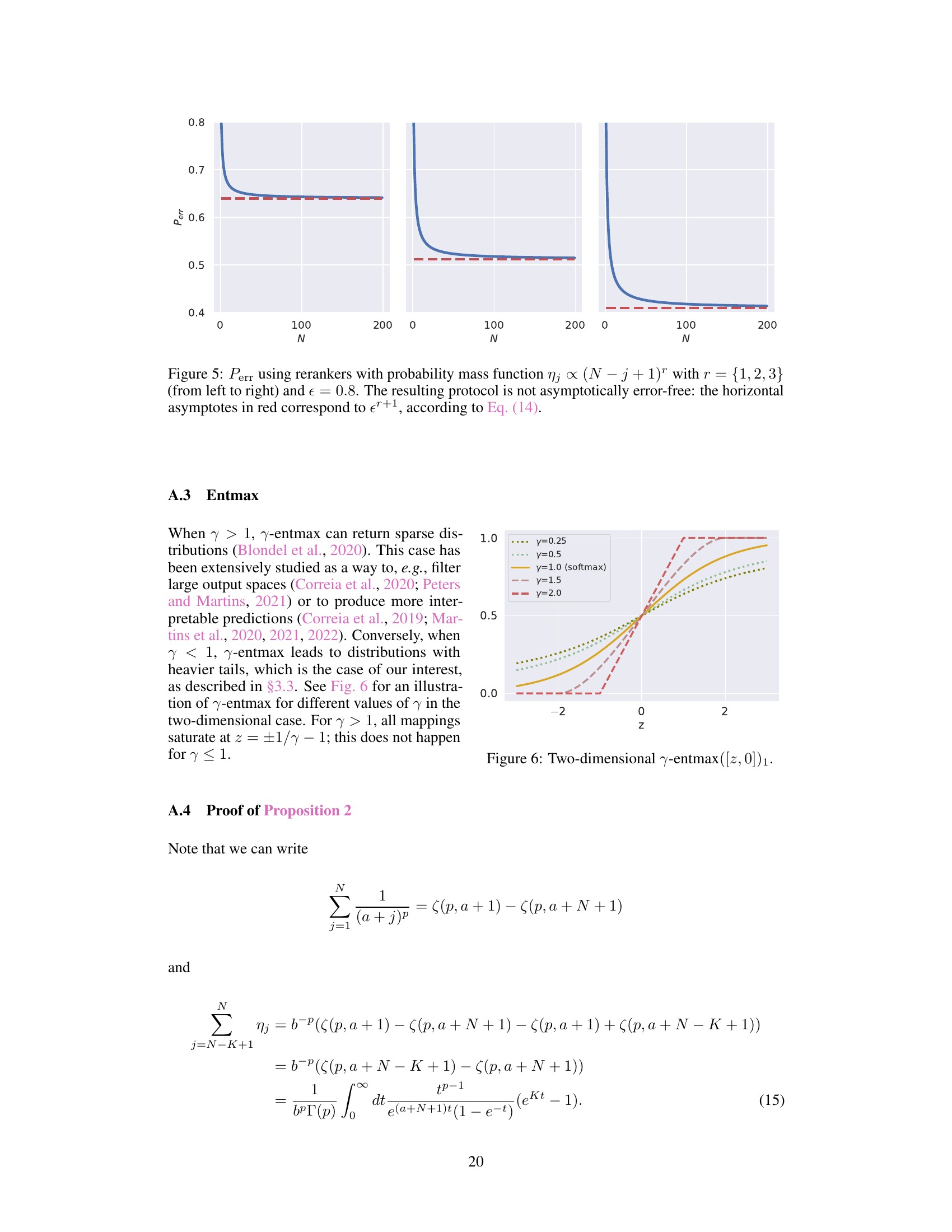
This figure shows the error probability (Perr) as a function of the number of hypotheses (N) for different rerankers. The rerankers used have probability mass functions of the form ηj × (N − j + 1)r, where r is a parameter controlling the shape of the distribution (r = 1, 2, and 3 are shown). The error probability approaches a horizontal asymptote, indicating that the protocol is not asymptotically error-free in these cases. The red dashed lines represent the theoretical asymptotes (εr+1), where ε is the base error probability. These plots demonstrate that even slightly imperfect rerankers may not guarantee asymptotically error-free performance.
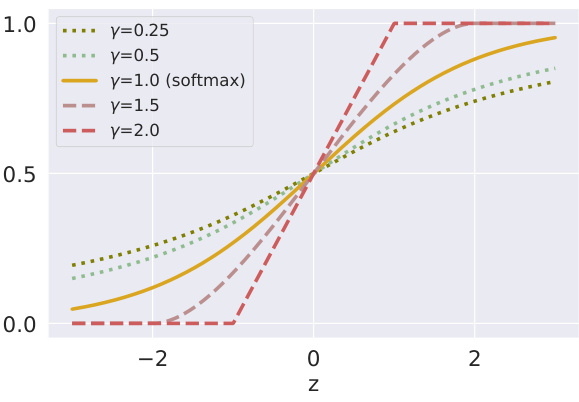
This figure shows how the log of the failure rate changes as the number of generated hypotheses increases for different values of the parameter e¯^ and a fixed error rate of 0.3. The left panel shows results for the Mallows model, while the right panel shows results for the Zipf-Mandelbrot model. Both panels illustrate that increasing the number of hypotheses reduces the failure rate, which is consistent with the paper’s argument that adding redundancy (i.e., generating multiple hypotheses) helps to improve the reliability of language models.
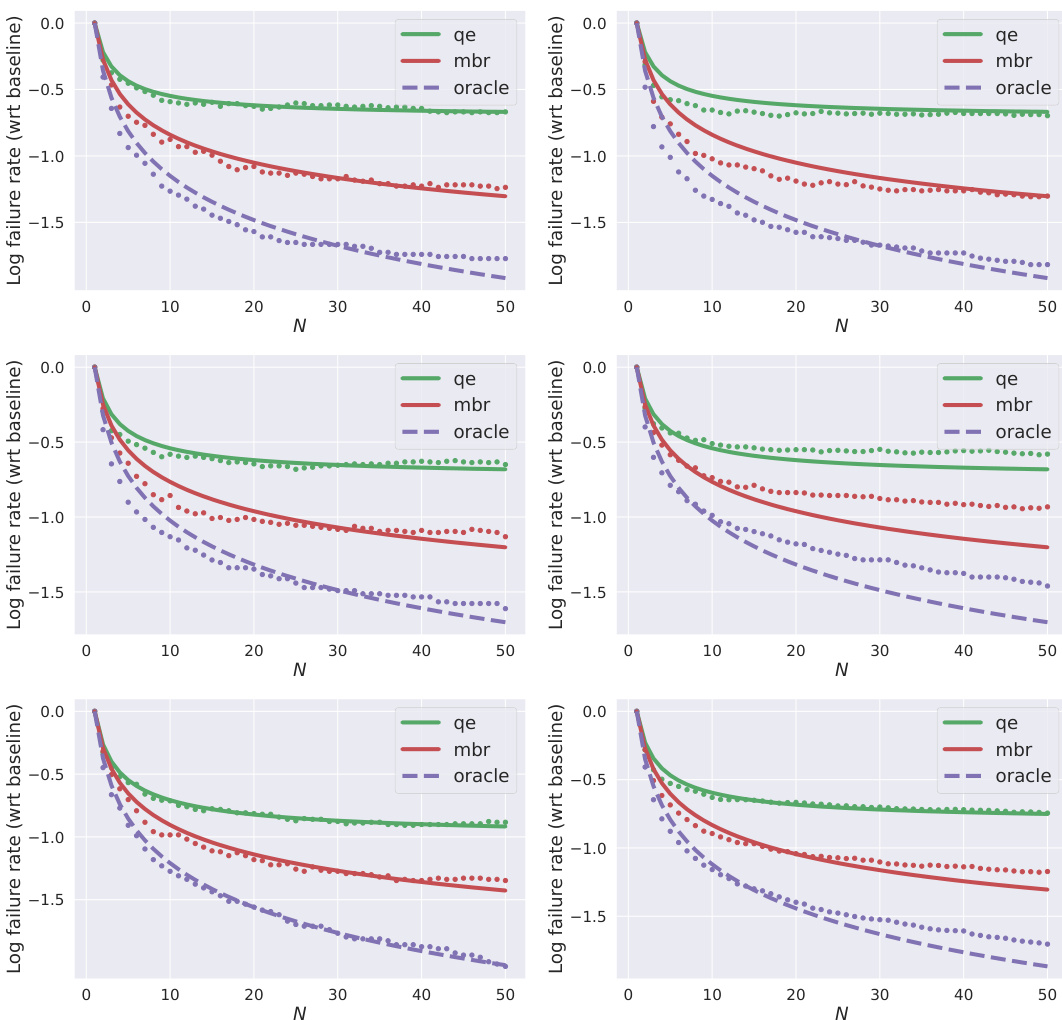
This figure shows the results of experiments on two different tasks: text-to-code generation and machine translation. The x-axis represents the number of hypotheses generated (N), and the y-axis represents the log of the failure rate (compared to a baseline). The plots show empirical data (dots) and model fits (lines). Solid lines represent imperfect rerankers, and dashed lines represent perfect rerankers. The top half of the figure shows the results for text-to-code generation, and the bottom half shows the results for machine translation.
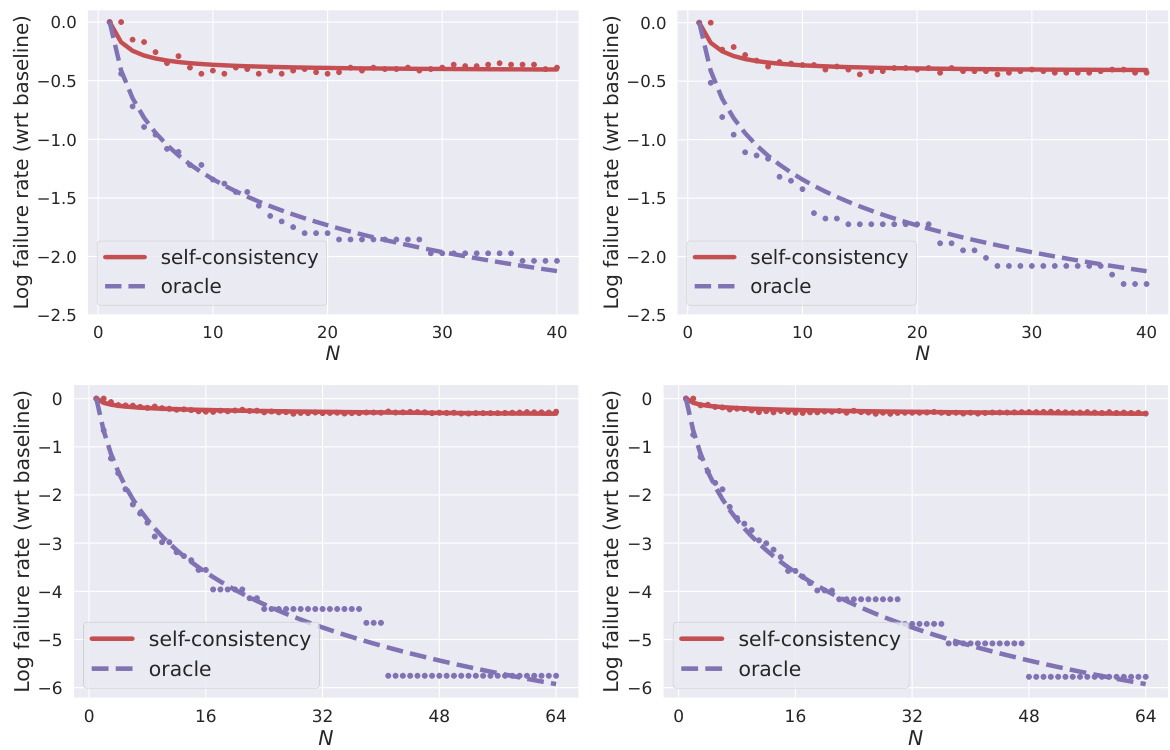
This figure shows the results of experiments on mathematical and commonsense reasoning benchmarks, evaluating the performance of the reranking protocol. The plots display the log of the failure rate (compared to a baseline) against the number of hypotheses (N). Separate plots are shown for development and test sets, and for imperfect and perfect rerankers. The goal is to see how error rates decrease as the number of hypotheses increases, and whether the performance matches predictions based on mathematical models presented in the paper. The top half presents results on the SVAMP dataset, while the bottom half presents results on the StrategyQA dataset.
Full paper#