An Analysis of Tokenization: Transformers under Markov Data

↗ OpenReview ↗ NeurIPS Proc. ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial for researchers in natural language processing (NLP) and deep learning. It provides a theoretical justification for tokenization, a widely used yet under-examined practice in language modeling. By demonstrating the limitations of transformer models without tokenization and establishing the near-optimality of simple unigram models with appropriate tokenization, this work challenges conventional wisdom and paves the way for designing more efficient and robust language models in the future. The findings and proposed framework open new avenues for investigating the critical role of tokenization and improving the generalization capabilities of NLP models.

Visual Insights

#

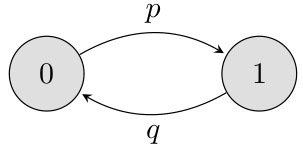
This figure shows a state diagram for a 2-state Markov chain. The states are labeled 0 and 1, and the transition probabilities are p (from state 0 to state 1) and q (from state 1 to state 0). The caption also describes how this model can be generalized to a kth-order Markov chain, where the probability of transitioning to a state depends only on the state k time steps prior. This is done by defining transition probabilities Pr(Xₙ = 1|Xₙ−k = 0) = p and Pr(Xₙ = 0|Xₙ−k = 1) = q.

This table shows how the BPE algorithm works on a specific dataset (equation 15 in the paper) that’s designed to highlight some aspects of BPE’s behavior. It illustrates the iterative merging process where frequently adjacent token pairs are combined into new tokens. The table tracks this process, showing how the dictionary evolves and tokens are replaced in each iteration. The purpose is to demonstrate how BPE’s behavior might not always lead to optimal generalization, as the resulting model might not generalize well to unseen sequences.

In-depth insights

#

Tokenization’s Role

#

The research paper delves into the critical role of tokenization in the performance of transformer-based language models. Tokenization, the process of breaking down text into smaller units (tokens), is often viewed as a necessary preprocessing step, despite efforts to circumvent it. The authors challenge this assumption by focusing on the behavior of transformers trained on simple Markov data. They demonstrate that without tokenization, transformers struggle to learn the underlying data distribution, effectively reducing to unigram models. This highlights tokenization’s crucial role in enabling transformers to capture higher-order dependencies within the data. The study then explores various tokenization methods, investigating how the choice of tokenizer impacts the model’s ability to learn near-optimally. They show that the appropriate tokenization allows even simple unigram models to achieve near-optimal performance. This rigorous analysis provides a strong justification for the continued use of tokenization in practical language modeling, offering a theoretical foundation to understand its significance.

Transformer Limits

#

The heading ‘Transformer Limits’ suggests an exploration of the inherent boundaries and constraints of transformer models. A thoughtful analysis would delve into the model’s capacity limitations concerning data complexity. Transformers, despite their success, struggle with long-range dependencies and the intricacies of complex, real-world data, often simplifying them into manageable representations. The section might examine how model size and training data affect performance, showing diminishing returns beyond certain thresholds. Theoretical discussions might explore the computational cost and sample efficiency, revealing that extremely large models might not always be the most efficient approach for certain tasks. Another aspect could be the model’s brittleness in handling noisy or adversarial data, leading to unexpected or incorrect outputs. The ’limits’ could also relate to the models’ difficulty in capturing nuanced linguistic features, particularly in low-resource scenarios. Finally, the section might discuss limitations concerning explainability and interpretability, emphasizing the inherent opacity of large transformer models.

BPE’s Efficiency

#

The analysis of Byte Pair Encoding (BPE)’s efficiency in the provided research paper involves a multifaceted investigation. The paper highlights BPE’s practical use in various language models, acknowledging its iterative dictionary construction method. This method merges frequent token pairs, recursively creating new tokens and resulting in an ordered mapping. However, the paper identifies a critical limitation: the standard BPE algorithm’s struggle with rare or unseen tokens due to dictionary size constraints. This leads to instability in generalization and increased cross-entropy loss. The research proposes a sequential variant of BPE to address this limitation by sample splitting, improving efficiency by learning at most one token per chunk of the training dataset. This modification mitigates the issues of rare tokens, leading to theoretically proven efficiency improvements in approximating the optimal cross-entropy loss, although the theoretical guarantees are less strong than with other tokenizers. The paper further reveals that the interaction between dictionary design and encoding algorithm significantly impacts the performance of any tokenizer; the choice of encoding algorithm must be considered when evaluating a tokenizer’s efficacy, as even well-designed dictionaries may fail to generalize optimally depending on the encoding method used.

Generalization Issues

#

The concept of generalization in the context of tokenization for language models is multifaceted. It probes the model’s ability to handle unseen data, going beyond the training corpus. A tokenizer’s success hinges on its generalization performance, not just its compression efficiency on the training set. The paper highlights that dictionaries might effectively compress training data yet fail to generalize to new sequences, leading to high cross-entropy loss. This emphasizes the critical interplay between the tokenizer and its encoding algorithm; an effective tokenizer must not only learn patterns in the training data but also generalize these patterns for effective modeling of novel sequences. This necessitates a shift from focusing solely on metrics like compression ratios to the more comprehensive measure of end-to-end cross-entropy, thereby better assessing a tokenizer’s true capability to learn and generalize from data.

Future Directions

#

Future research could explore more complex data-generating processes beyond simple Markov models to better understand the behavior of transformers and the role of tokenization. Investigating the interaction between tokenization algorithms and the downstream models (e.g. transformers) is crucial. Theoretical analysis could be extended to cover more realistic scenarios, such as non-ergodic Markov chains and those with more complex dependencies, as well as other types of tokenizers and their associated generalization properties. The effect of tokenization on the training dynamics of transformers, and particularly how it affects the optimization landscape, warrants further exploration. Finally, a deeper examination of how tokenization biases the performance of LLMs on downstream tasks, including fairness and robustness issues, is needed to better understand their overall impact and guide the design of future, more effective tokenization strategies. Exploring the impact of varying the size of the vocabulary, and particularly smaller vocabulary sizes more relevant to practical deployment limitations, could have significant implications for resource-efficient model development.

More visual insights

#

More on figures

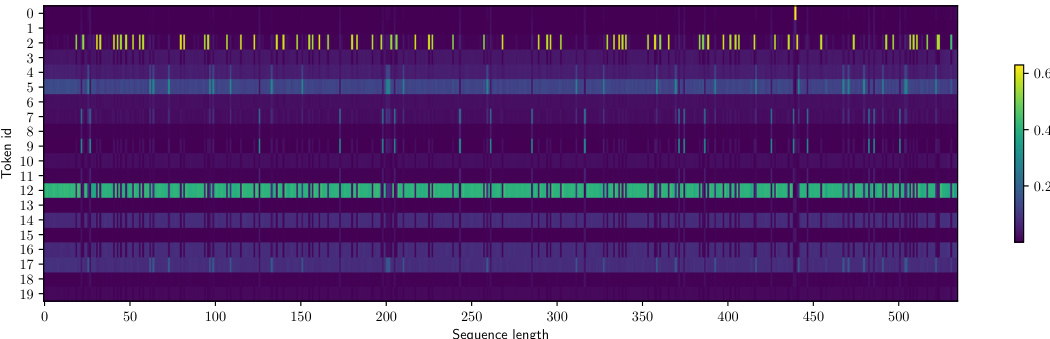
This figure visualizes the token distribution predicted by a transformer model at various positions within a test sequence. The transformer is trained on tokenized data using a learned BPE encoder with a dictionary size of 20. Each vertical column represents the probability distribution of the next token, given the preceding tokens. The relative uniformity of the columns across the x-axis (sequence length) suggests the model learns a unigram model, even though the data source is a more complex kth-order Markov process.

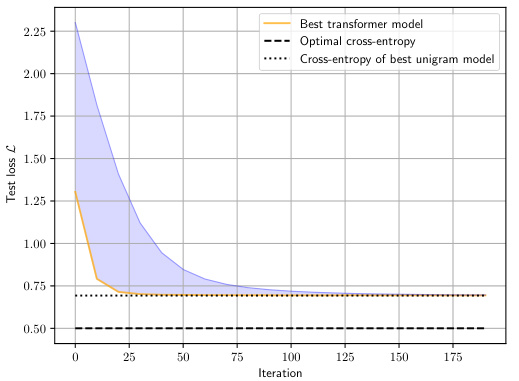
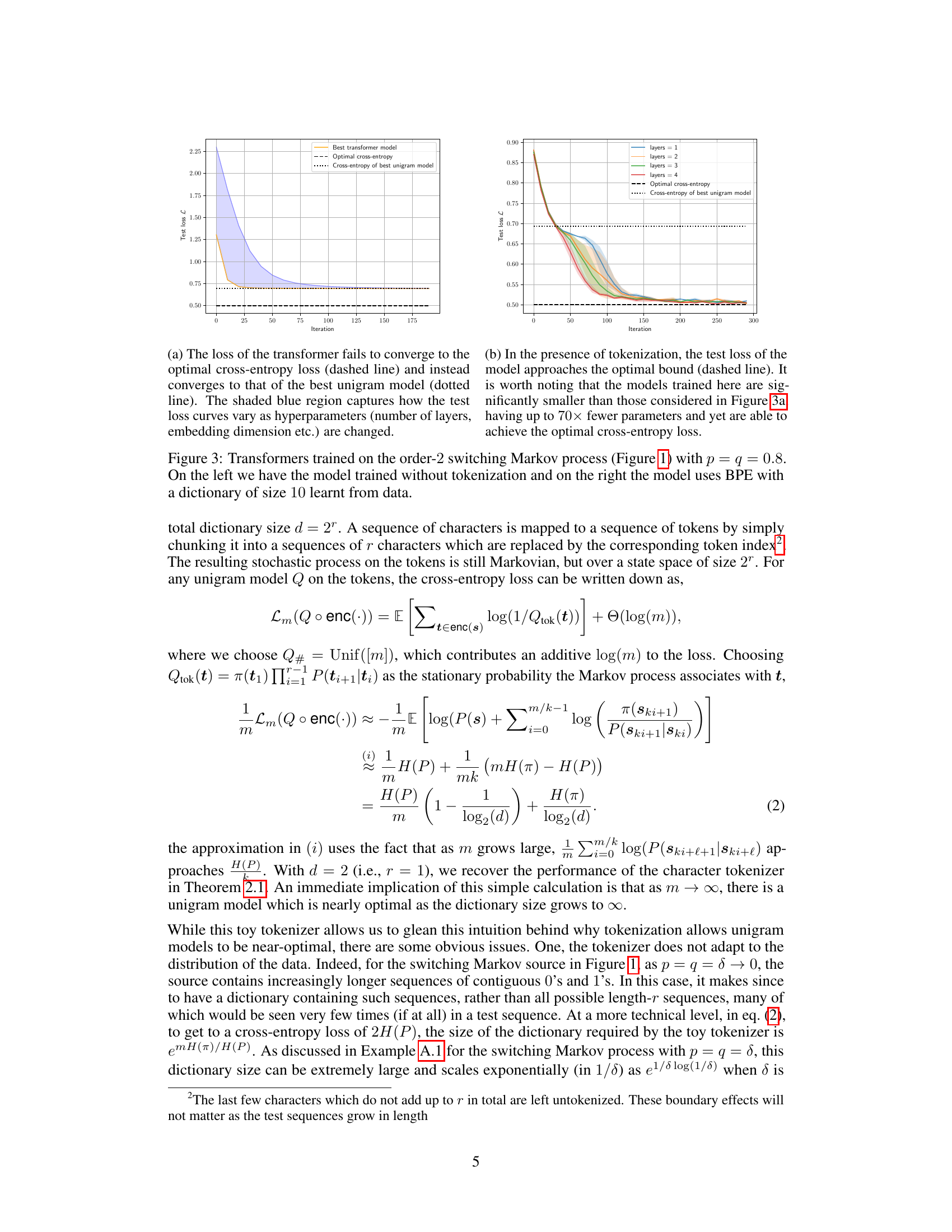
This figure compares the performance of transformers trained on a simple Markov process with and without tokenization. The left panel shows that without tokenization, the model fails to learn the data distribution, converging to a unigram model instead. In contrast, the right panel shows that with the addition of BPE tokenization, the transformer is able to learn the target distribution successfully, achieving near-optimal cross-entropy loss. This illustrates the significant impact of tokenization on the performance of transformers on non-i.i.d data.

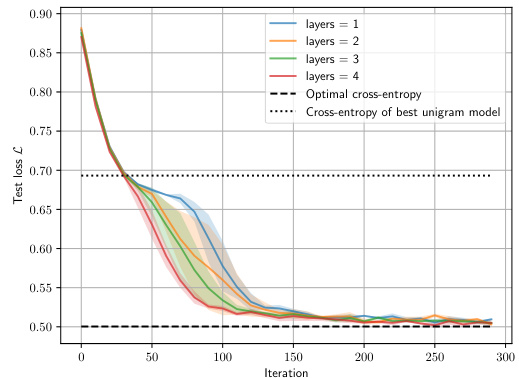
This figure compares the training performance of transformers on an order-2 Markov process with and without tokenization. The left panel shows that without tokenization, the transformer’s loss converges to that of the best unigram model, failing to learn the true Markov process. The right panel demonstrates that with BPE tokenization (dictionary size 10), the transformer achieves near-optimal cross-entropy loss, demonstrating that tokenization helps transformers effectively model higher-order dependencies in data.

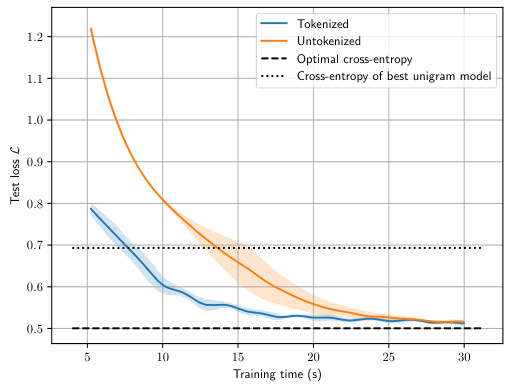
This figure shows the training loss curves for transformer models trained on a second-order Markov process with and without tokenization. The left panel displays the loss for a model trained without tokenization, showing it plateaus at the performance of a unigram model. The right panel shows the loss for a model trained with BPE tokenization, demonstrating that it reaches near-optimal performance.

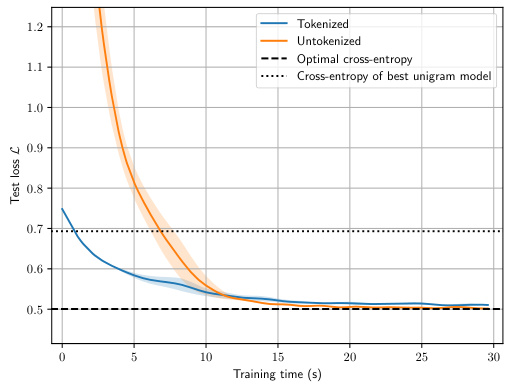
This figure compares the training performance of transformer models with and without tokenization on a second-order Markov process. The left panel shows that without tokenization, the model fails to surpass the performance of a unigram model. The right panel demonstrates that with BPE tokenization (dictionary size 10), the model achieves near-optimal performance, indicating the importance of tokenization for transformer models trained on data with dependencies.

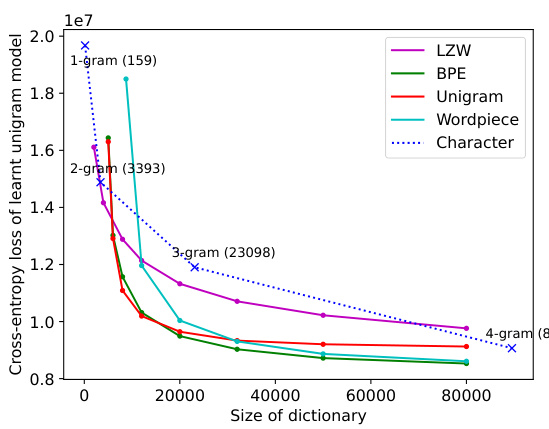
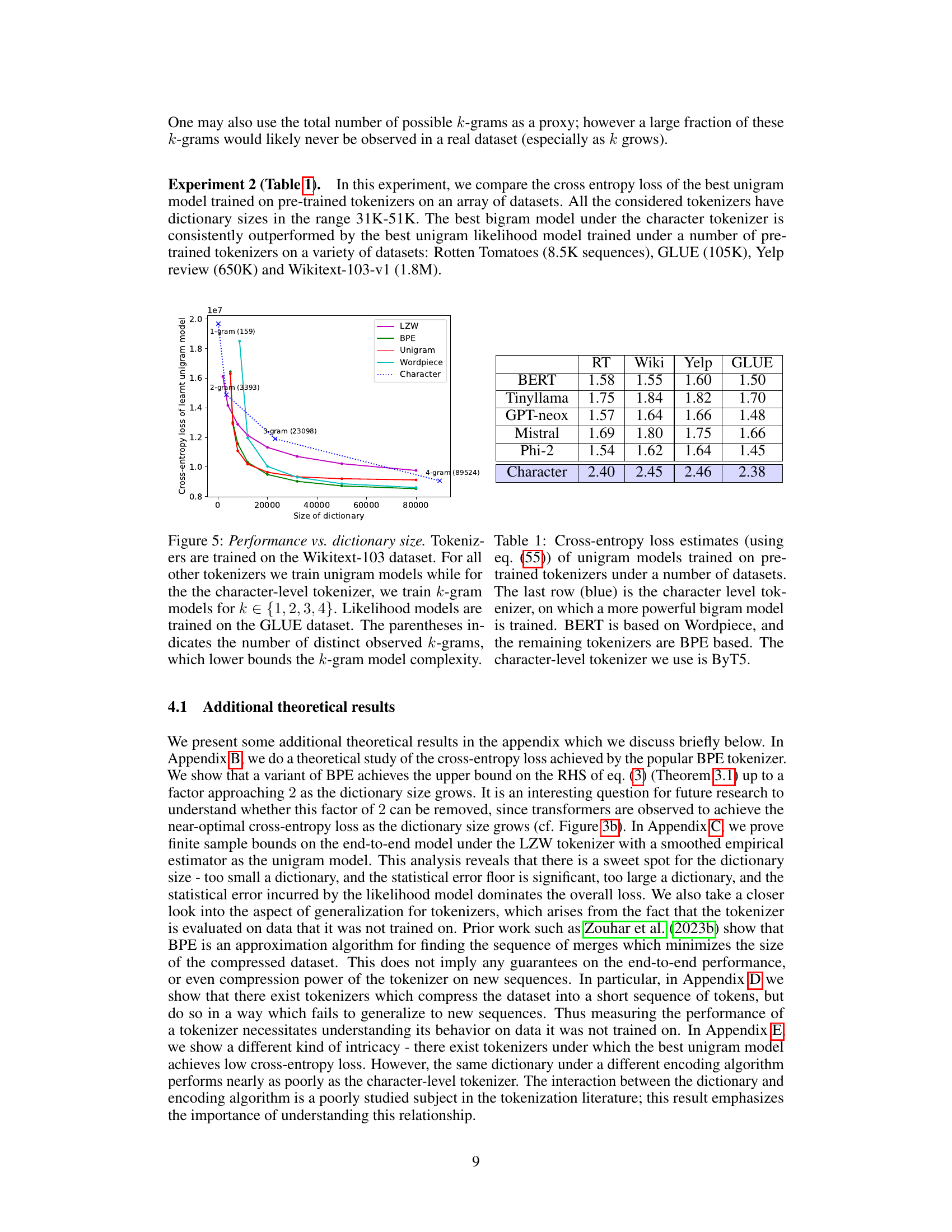
This figure compares the performance of different tokenizers on the GLUE dataset in terms of cross-entropy loss. The x-axis shows the size of the dictionary used, and the y-axis represents the cross-entropy loss. The figure shows that tokenizers trained on Wikitext-103 significantly outperform the character-level tokenizer, highlighting the impact of tokenization on model performance. The different colored lines represent the different tokenizers (LZW, BPE, Unigram, Wordpiece, and Character), and the different markers within each line shows the performance of k-gram models (k=1, 2, 3, 4).

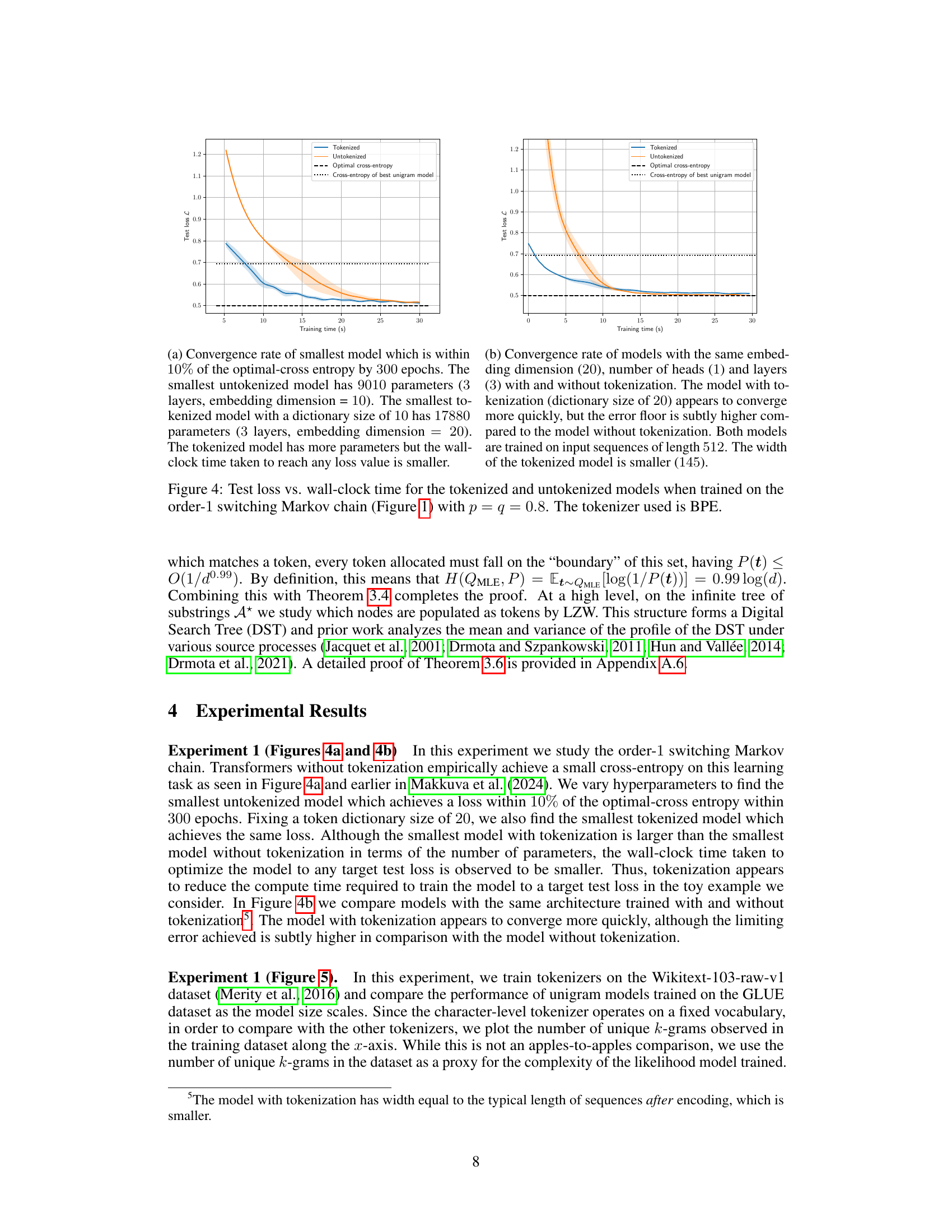
This figure shows the training loss curves for transformers trained on a simple Markov process. The left plot displays the results when no tokenization is used, while the right plot shows the improved results when using a Byte Pair Encoding (BPE) tokenizer with a dictionary of size 10. The figure highlights the significant improvement in convergence speed and final loss when tokenization is applied.

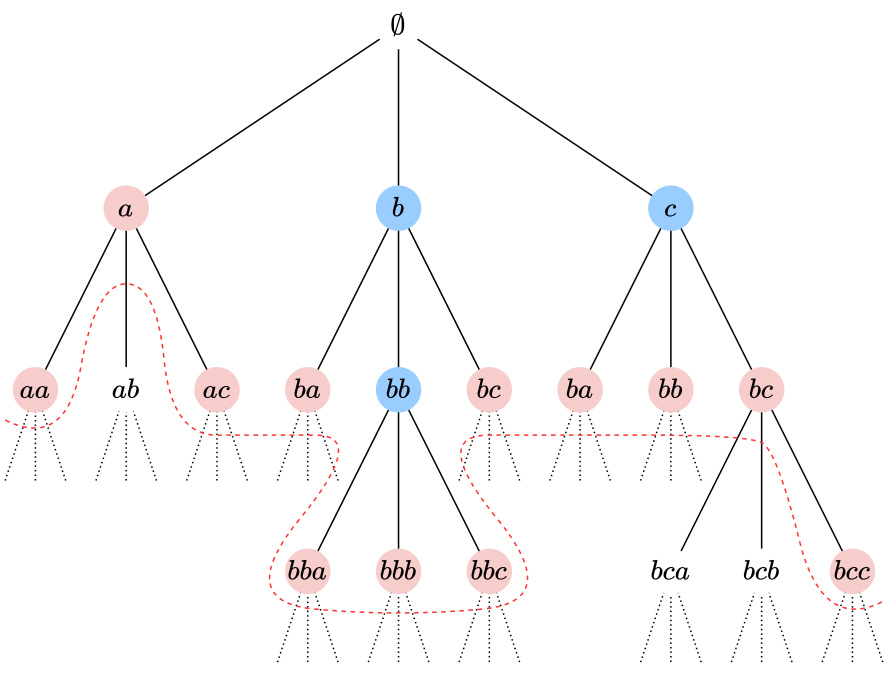
This figure is a tree diagram illustrating the heavy-hitting property of a dictionary. Each node represents a substring. The circled nodes show substrings that are tokens. Red nodes show substrings that are maximal tokens; that is, tokens that are not prefixes of any other tokens in the dictionary. The red dotted line marks a boundary above which tokens are never selected by the greedy encoder, illustrating the fact that these maximal tokens have a low probability of appearing. The heavy hitting property is that these maximal tokens have a probability that is less than 1/dβ.

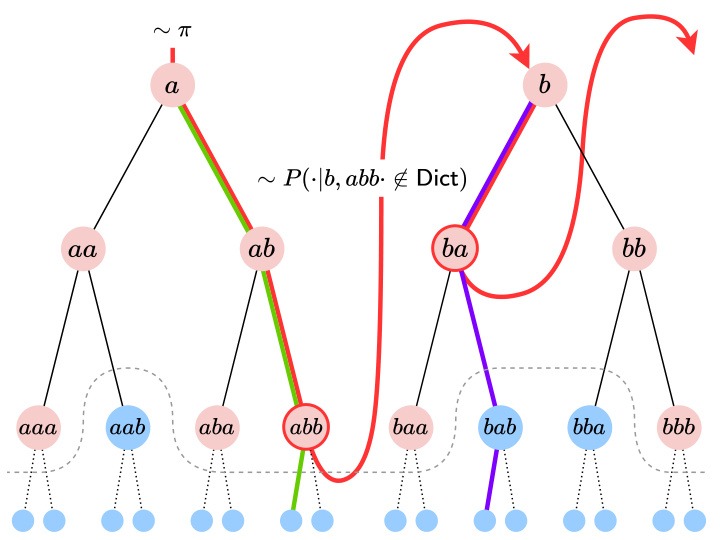
This figure illustrates the process of jointly generating a sequence and its greedy encoding using a dictionary of substrings. It starts by sampling a character from the stationary distribution and then iteratively builds a sequence and its encoding by selecting the longest token-prefix from an infinite trajectory on the tree, ensuring that the selected token’s extension is not already present in the dictionary. This process continues until a complete sequence and its encoding are generated.

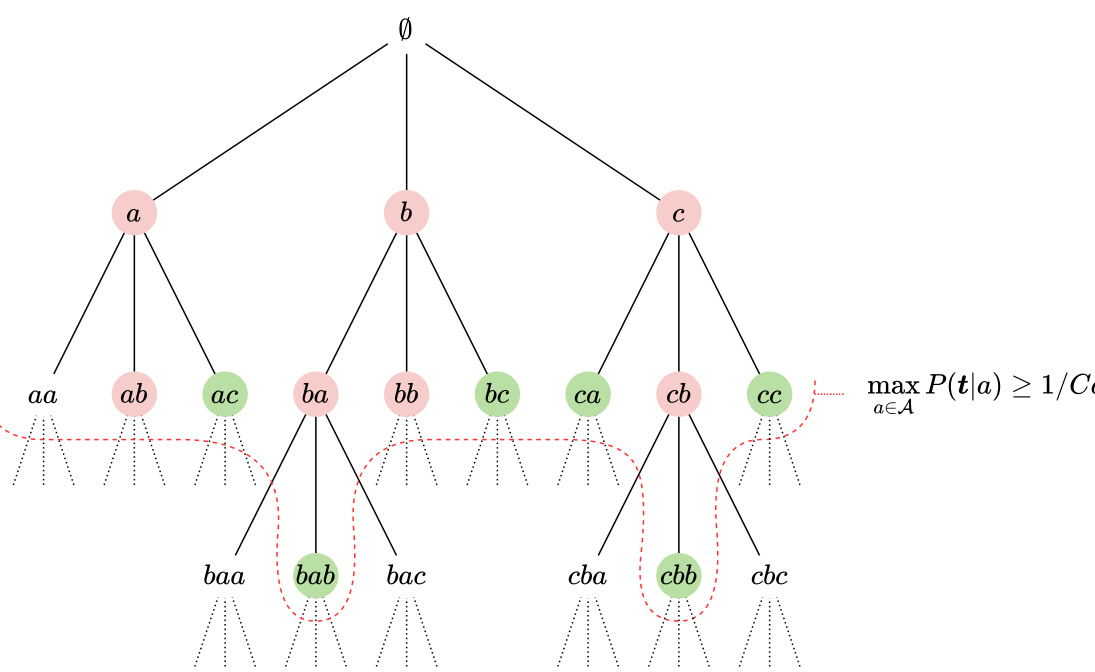
This figure shows a tree structure representing substrings generated from a given alphabet. Nodes represent substrings and edges represent the addition of a character. Red nodes represent maximal tokens in the dictionary, meaning that no longer substring containing the token is also a token in the dictionary. The figure illustrates the heavy-hitting property, which ensures that maximal tokens have low probabilities and that the greedy encoder assigns tokens far from the root node.

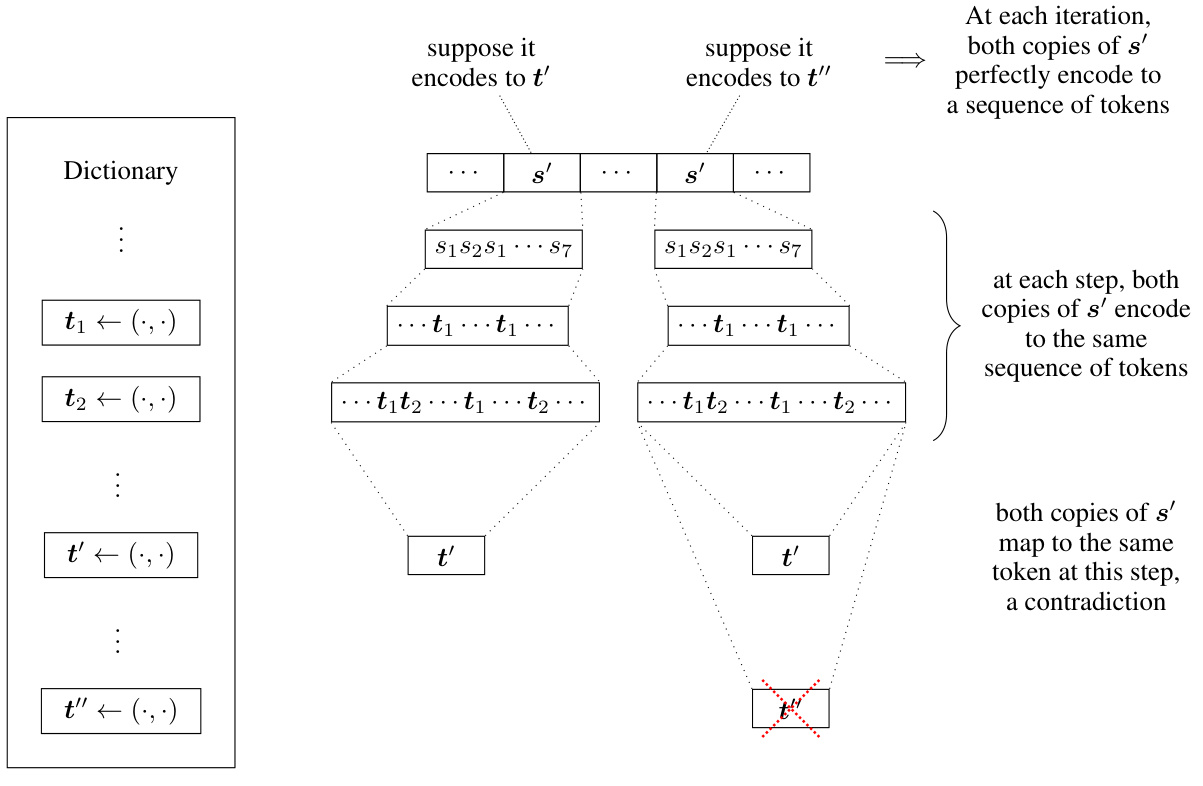
This figure illustrates the proof of Lemma B.6 by contradiction. It shows that if two tokens decode to the same character substring, then at each step in the merging process, these occurrences of the substring must map to the same sequence of tokens, which leads to a contradiction. This demonstrates that tokens assigned by Algorithm 1 must have distinct character representations.

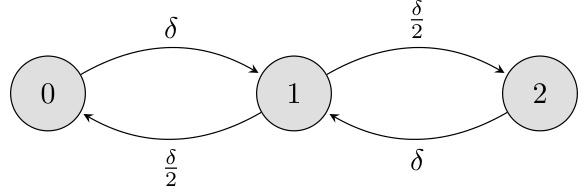
This figure shows a state diagram of a 2-state Markov chain. The probability of transitioning from state 0 to state 1 is δ, and from state 1 to state 0 is also δ. The self-transition probabilities (remaining in the same state) are 1-δ. The caption also mentions a kth-order extension where the state transitions depend only on the kth previous state, with probabilities p and q for transitioning to state 1 from state 0, and state 0 from state 1, respectively.

Full paper

#