↗ OpenReview ↗ NeurIPS Proc. ↗ Chat
TL;DR#
Large Language Models (LLMs) are prone to generating inaccurate information, and effectively measuring uncertainty in long-form text remains a challenge. Current methods often lack granularity, hindering precise assessment of individual claims’ reliability. This limits the ability to build trust in LLM outputs and safely deploy them in real-world applications.
This paper introduces Graph Uncertainty, a novel framework that models the relationship between LLM generations and claims as a bipartite graph. By employing graph centrality metrics (like closeness centrality), it provides more nuanced uncertainty estimations at the claim level. Further, an uncertainty-aware decoding technique uses these estimates to filter out unreliable claims, resulting in more factual and informative responses. Experiments show significant performance gains in factuality and overall accuracy, exceeding existing techniques.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working with LLMs, particularly those focusing on long-form text generation and factuality. By introducing a novel graph-based uncertainty estimation framework, it offers a significant improvement over existing methods. It also proposes an uncertainty-aware decoding technique, which directly impacts the factuality of generated text, and opens exciting new avenues for future research in LLM reliability and trustworthiness.
Visual Insights#

This figure illustrates the Graph Uncertainty framework for claim-level uncertainty estimation. It begins with sampling multiple responses from a large language model (LLM) given a prompt (a). Each response is then decomposed into individual claims (b). A bipartite graph is constructed, linking claims to the responses that support them (c). Finally, graph centrality metrics (degree, eigenvalue, PageRank, closeness, etc.) are used to estimate the uncertainty of each claim (d). Claims with high uncertainty are marked with an ‘X’, while those with low uncertainty are marked with a checkmark. This framework provides a more granular way to assess uncertainty compared to methods that only focus on overall response uncertainty.

This table presents the results of a comparative analysis of claim-level uncertainty estimation methods. It shows AUROC and AUPRC-Negative scores for various methods (including different centrality metrics and baselines) across two datasets (FactScore and PopQA) and different numbers of LLM samples. Statistically significant improvements are highlighted, indicating the superior performance of closeness centrality.
In-depth insights#
Graph Uncertainty#
The concept of ‘Graph Uncertainty’ presents a novel approach to quantifying uncertainty in large language model (LLM) outputs, particularly within long-form text generation. Instead of relying solely on traditional methods like self-consistency which utilize degree centrality, this framework leverages the power of graph theory to represent the relationships between LLM generations and the claims made within them as a bipartite graph. This allows for a more nuanced understanding of uncertainty, moving beyond a simple aggregate score. By employing graph centrality metrics such as closeness centrality, a more sophisticated measure of claim importance is obtained, providing consistent improvements in claim-level uncertainty estimation. This granular approach enables a better understanding of which claims are reliable versus unreliable within the LLM-generated text. Furthermore, the integration of graph-based uncertainty metrics into uncertainty-aware decoding techniques provides a significant boost to the factuality of generated text, while simultaneously preserving informativeness. This novel approach marks a significant advancement in dealing with the inherent challenges of factual accuracy and uncertainty in LLM outputs.
Centrality Metrics#
Centrality metrics, in the context of graph-based uncertainty analysis for large language models (LLMs), offer a powerful lens for understanding the reliability of individual claims within LLM-generated text. By representing the relationships between LLM generations and claims as a bipartite graph, centrality metrics quantify the ‘importance’ of each claim node, essentially measuring its influence or connectivity within the network. Different centrality measures (degree, betweenness, closeness, eigenvector, PageRank) offer unique perspectives on this importance, revealing different facets of claim reliability. The choice of centrality metric significantly impacts the accuracy of uncertainty estimation. While simpler metrics like degree centrality mirror existing self-consistency methods, more sophisticated metrics like closeness centrality can provide more granular, informative uncertainty estimations, revealing consistent improvements in metrics such as AUPRC. This framework provides a significant advance over previous methods by moving beyond simple counts and leveraging the rich structure and relationships inherent in the claim-response graph for a more nuanced and precise uncertainty assessment.
Decoding Methods#
Decoding methods in large language models (LLMs) are crucial for generating coherent and high-quality text. The choice of decoding method significantly impacts the final output’s fluency, accuracy, and overall quality. Greedy decoding, a simple approach, selects the word with the highest probability at each step, often leading to repetitive or unnatural text. Beam search improves upon greedy decoding by considering multiple candidate sequences simultaneously, broadening the search space for better results but increasing computational cost. Sampling-based methods, such as top-k or nucleus sampling, introduce randomness by selecting from a subset of the most probable words, fostering creativity but potentially sacrificing coherence. Uncertainty-aware decoding represents a sophisticated approach that incorporates uncertainty estimates into the decoding process, allowing the model to preferentially select more reliable words or claims, thereby enhancing the overall factuality and reducing hallucinations. This approach, however, requires accurate uncertainty estimation methods. The effectiveness of each decoding strategy depends on the specific application and desired trade-off between fluency, creativity, and accuracy. Advanced methods may integrate reinforcement learning or external knowledge sources to further refine the generation process.
Factuality Gains#
Analyzing factuality gains in large language models (LLMs) is crucial for assessing their reliability and trustworthiness. Significant factuality gains often result from enhanced uncertainty estimation methods, allowing the model to distinguish between reliable and unreliable claims within its generated text. This improved discrimination empowers uncertainty-aware decoding techniques, which selectively retain high-confidence claims, thus bolstering the factual accuracy of the overall output. Graph-based approaches, which represent the relationship between generated claims and supporting evidence as a graph, show particular promise in achieving substantial factuality gains. These methods leverage graph centrality measures to identify the most reliable claims, offering a more nuanced approach compared to simpler self-consistency techniques. Specific centrality metrics, such as closeness centrality, appear particularly effective, demonstrating consistent improvements over baseline methods across various evaluation datasets. The achieved factuality gains, expressed as percentages, reflect the extent to which these advanced techniques mitigate the problem of hallucinations in LLMs, ultimately advancing the goal of producing more reliable and informative responses.
Future Work#
The research paper’s ‘Future Work’ section could explore several promising avenues. Improving the efficiency of the graph construction process is crucial, as it currently increases inference time and computational overhead. This could involve exploring more efficient graph algorithms or alternative methods for representing the relationship between claims and responses. Further research could also investigate how to handle scenarios with dependent claims more effectively, as the current claim decomposition method assumes claims are independent. The system’s robustness under different LLMs and prompts should also be assessed more comprehensively. Additionally, exploring different graph centrality metrics beyond those already tested would be valuable, particularly those designed to be more robust to noisy data. Finally, extending the framework to incorporate uncertainty estimation from different sources and investigating the integration of this framework with other factuality-enhancing techniques, such as retrieval-augmented generation, will significantly enhance the system’s capabilities. Addressing these points would strengthen the paper’s impact and establish the method’s viability in real-world applications.
More visual insights#
More on figures
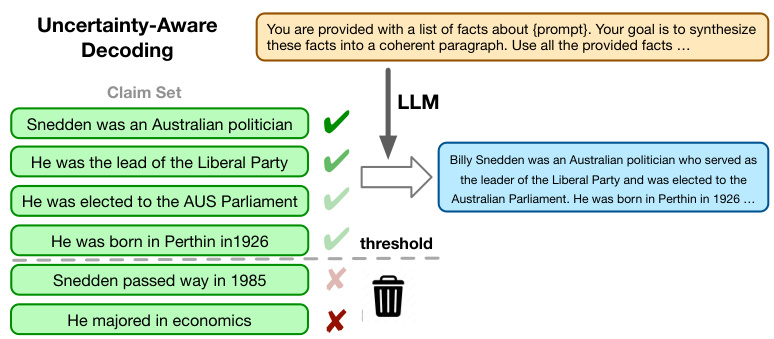
This figure illustrates the uncertainty-aware decoding framework. It takes as input a set of claims with associated uncertainty scores (obtained from the graph uncertainty method shown in Figure 1). Claims with uncertainty scores below a threshold are selected. An LLM then synthesizes these selected claims into a coherent paragraph. The threshold parameter controls the trade-off between factuality (fewer false claims) and informativeness (more claims included in the final output).

The figure shows the precision of claims (y-axis) plotted against the number of true claims (x-axis) for different methods including greedy decoding, CoVe, and several variants of Uncertainty-Aware Decoding (UAD). Different UAD variants use different uncertainty estimation methods to filter claims before generating the response. The graph illustrates the trade-off between factuality (precision of claims) and informativeness (number of true claims). UAD methods, particularly those employing the closeness centrality metric, show a better trade-off compared to non-UAD baselines. The shaded regions represent confidence intervals.
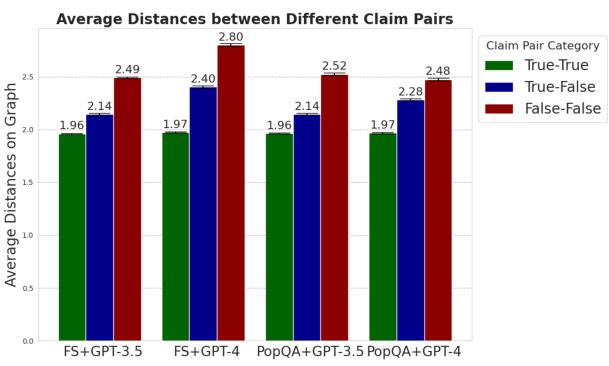
This figure presents the results of an ablation study to analyze the effectiveness of closeness centrality for uncertainty estimation. Subfigure (a) shows that false claims have a greater average distance to other claims in the semantic graph compared to true claims, demonstrating the effectiveness of the closeness centrality metric. Subfigure (b) demonstrates that increasing the number of responses used to construct the claim node set consistently improves performance, highlighting the impact of the graph structure on uncertainty estimation. The results show that closeness centrality is effective at discriminating between true and false claims because of the relationships between nodes within the graph. More connections indicate higher centrality and a higher likelihood of factual accuracy.

This figure presents an ablation study to analyze the effectiveness of closeness centrality in discriminating between true and false claims and how the performance changes with the number of responses used to construct the claim node set. The left subplot (a) shows that false claims have a greater average distance to other claims than true claims in the semantic graph, supporting the use of closeness centrality. The right subplot (b) demonstrates that increasing the number of responses consistently improves performance in uncertainty estimation, highlighting the benefit of using more granular graph information.
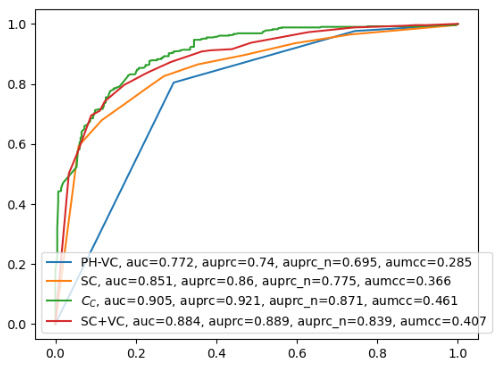
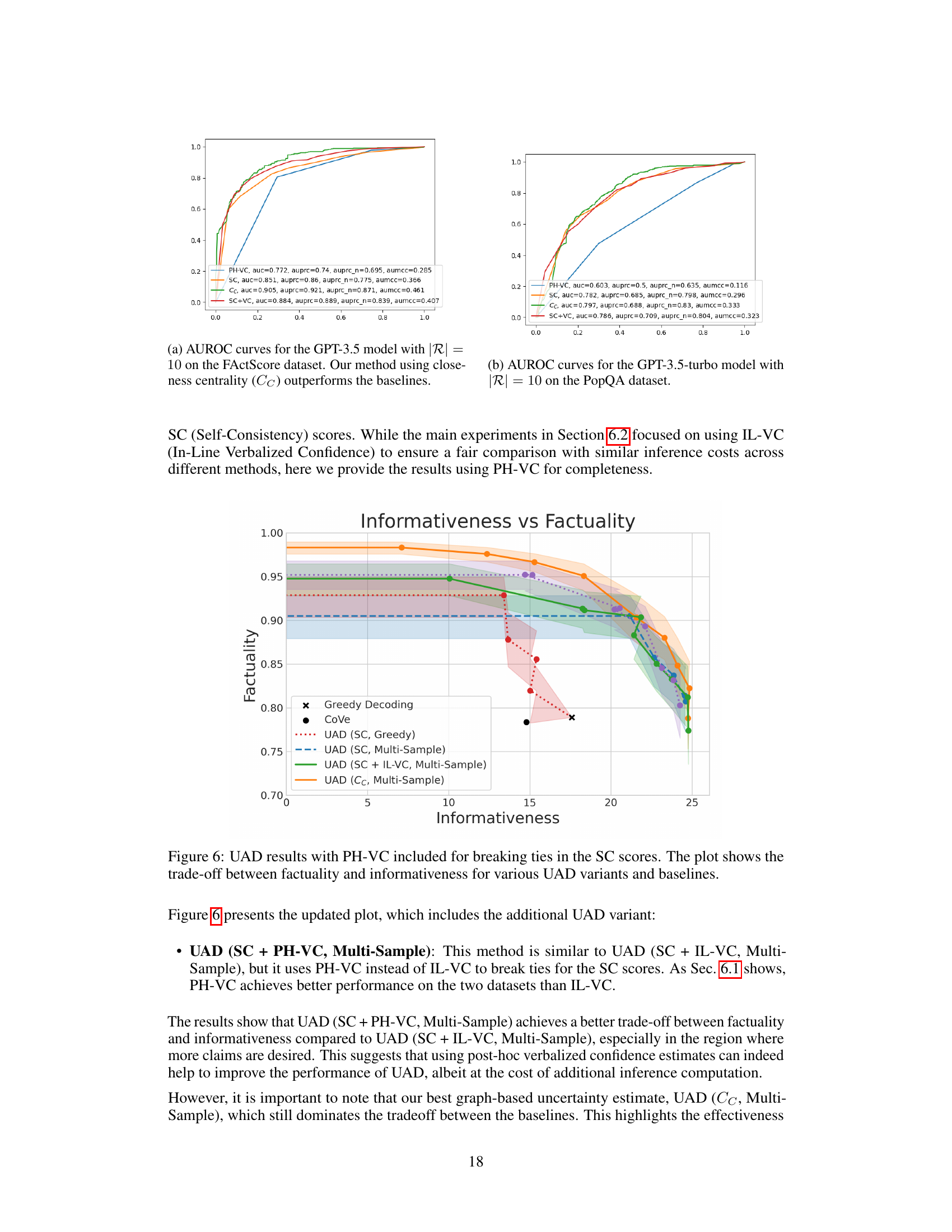
This figure shows the AUROC curves for different uncertainty estimation methods on the FactScore dataset using the GPT-3.5 model with 10 response samples. The closeness centrality (CC) method significantly outperforms baseline methods such as post-hoc verbalized confidence (PH-VC), self-consistency (SC), and self-consistency combined with verbalized confidence (SC+VC), demonstrating its superior ability to distinguish between true and false claims.

This figure shows the results of the Uncertainty-Aware Decoding (UAD) method compared to other baselines (greedy decoding and CoVe). The x-axis represents the number of true claims, while the y-axis represents the precision of claims (factuality). Each curve represents a different threshold for filtering claims based on uncertainty scores. The results show that UAD with closeness centrality consistently outperforms other methods, achieving a better trade-off between factuality and informativeness.

This figure compares different decoding methods for evaluating the trade-off between the factuality and informativeness of the generated responses. The x-axis represents the informativeness (number of true claims), and the y-axis represents the factuality (precision of claims). The plot shows the Pareto frontier, illustrating the best possible trade-offs between factuality and informativeness. UAD (Uncertainty-Aware Decoding) methods consistently achieve a better trade-off than greedy decoding and CoVe baselines, demonstrating the effectiveness of incorporating uncertainty estimates into the decoding process.
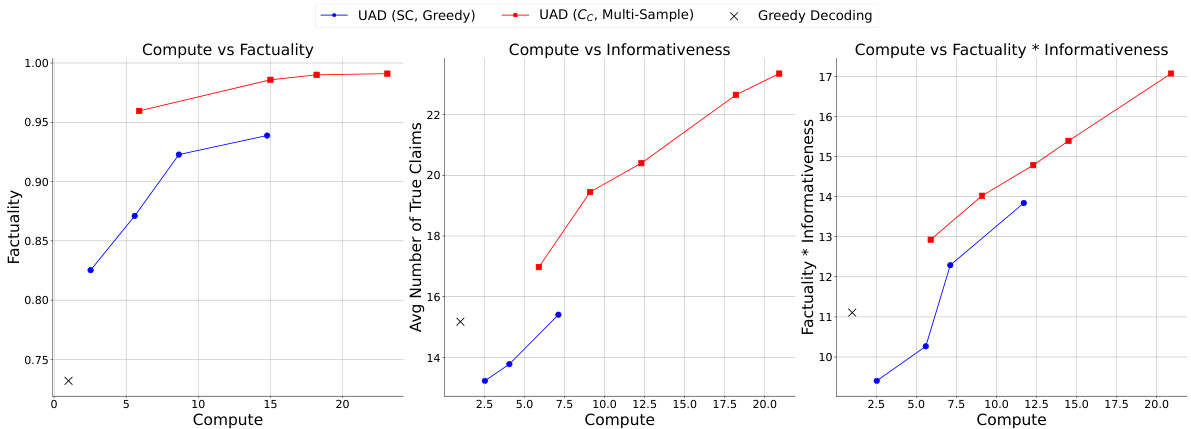
This figure shows the results of the Uncertainty-Aware Decoding (UAD) method. It compares the performance of UAD using different uncertainty estimation methods (Self-Consistency with greedy decoding, Self-Consistency with multi-sample decoding, Self-Consistency + In-line Verbalized Confidence with multi-sample decoding, and Closeness Centrality with multi-sample decoding) against greedy decoding and CoVe baselines. The x-axis represents the number of true claims, and the y-axis represents the precision of the claims. The figure demonstrates that UAD with better claim-level uncertainty estimation achieves a better balance between factuality and informativeness.
More on tables
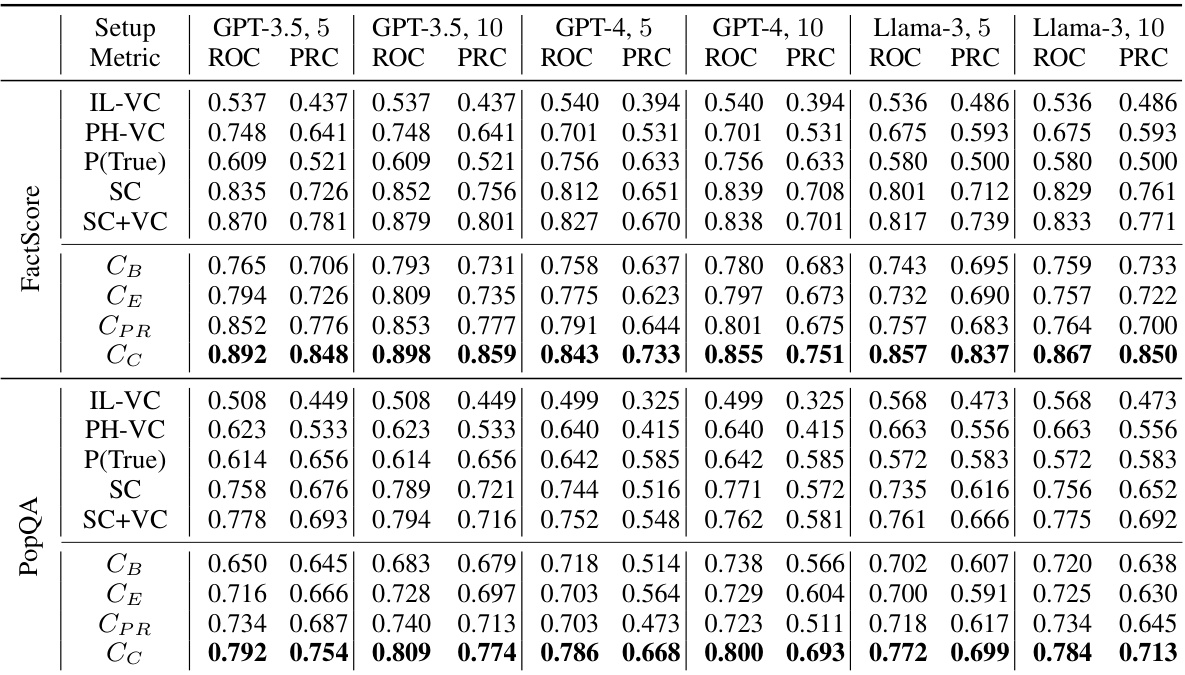
This table presents the results of a comparative analysis of different claim-level uncertainty estimation methods. It compares the Area Under the ROC Curve (AUROC) and Area Under the Precision-Recall Curve for the negative class (AUPRC-Negative) across various models (GPT-3.5, GPT-4, Llama-3), numbers of response samples (|R|=5 or 10), and uncertainty estimation methods (including closeness centrality, self-consistency, and verbalized confidence). Statistically significant improvements are highlighted. The table helps to show that the closeness centrality method outperforms other methods for estimating uncertainty at the claim level.
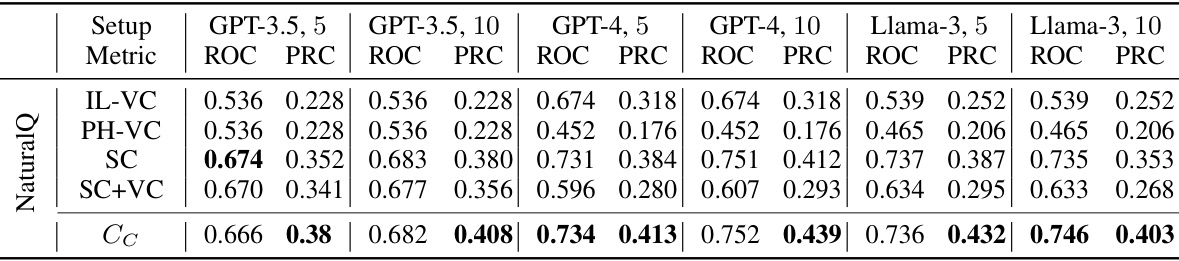
This table presents the results of a systematic comparison of different claim-level uncertainty estimation methods. It compares the Area Under the ROC Curve (AUROC) and the Area Under the Precision-Recall Curve for the Negative class (AUPRC-Negative) across various models (GPT-3.5, GPT-4, Llama-3), dataset (FactScore, PopQA), and number of response samples (|R|=5, |R|=10). The methods compared include several baselines (Verbalized Confidence, Self-Consistency) and the proposed Graph Uncertainty method using various centrality metrics (degree, betweenness, eigenvector, PageRank, closeness). Statistically significant improvements (p<0.05) are highlighted in bold.
Full paper#