↗ OpenReview ↗ NeurIPS Proc. ↗ Chat
TL;DR#
Coresets are subsets of large datasets used to speed up machine learning algorithms, but creating effective coresets is challenging. This paper investigates using Determinantal Point Processes (DPPs), which are probabilistic models that encourage diversity in the selected samples, to build coresets. Existing methods primarily relied on independent sampling, which often lacks diversity and can result in less effective coresets. The main issue is that the effectiveness of independent sampling-based coresets is limited.
This research leverages the unique properties of DPPs to tackle the challenge of coreset construction. The authors provide a novel theoretical framework by framing coreset loss as a linear statistic, linking the problem to concentration phenomena in DPPs. They derive new concentration inequalities that work for very general DPPs, going beyond what was previously possible, allowing for non-symmetric kernels and vector-valued functions. Experiments validate that DPP-based coresets are smaller and more accurate than those from independent sampling, offering significant advantages.
Key Takeaways#
Why does it matter?#
This paper is crucial because it demonstrates that Determinantal Point Processes (DPPs) can build smaller and more accurate coresets compared to traditional methods. This has significant implications for machine learning, offering computational efficiency in large-scale applications while maintaining accuracy. It also advances the theoretical understanding of DPPs, providing valuable tools for researchers working with concentration inequalities and linear statistics.
Visual Insights#
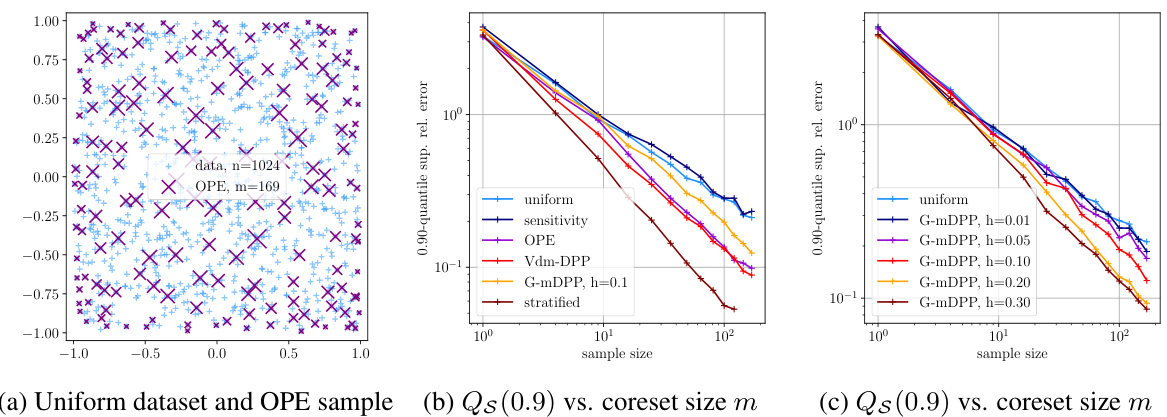
This figure shows the results of an experiment comparing different coreset construction methods on a uniform dataset. Panel (a) displays a scatter plot of the uniform dataset with an overlaid sample from an orthogonal polynomial ensemble (OPE) based DPP. Panel (b) presents a log-log plot illustrating the 0.90-quantile of the supremum relative error (a measure of coreset quality) against the coreset size (m) for various methods: uniform sampling, sensitivity-based sampling, OPE, Vdm-DPP, G-mDPP (with varying bandwidths h), and stratified sampling. Panel (c) is another log-log plot showing the same error metric (0.90-quantile of supremum relative error) versus the coreset size, focusing on the performance of G-mDPP across different bandwidths (h). The results demonstrate the superior performance of DPP-based methods, especially OPE and Vdm-DPP, compared to independent sampling methods (uniform and sensitivity) for achieving high accuracy coresets with fewer data points.
Full paper#