↗ OpenReview ↗ NeurIPS Proc. ↗ Chat
TL;DR#
Quasi-Newton methods, particularly the BFGS algorithm, are popular for optimization due to their speed and efficiency. However, existing analyses mostly focus on local convergence, leaving a gap in our understanding of their global behavior, especially with inexact line searches that are commonly used in practice. This limits the ability to precisely predict their performance and potentially hinder the development of improved variants.
This research paper addresses these issues by providing the first explicit and non-asymptotic global convergence analysis of the BFGS method with an inexact line search satisfying the Armijo-Wolfe conditions. The analysis shows that BFGS achieves both global linear and superlinear convergence rates. Crucially, the linear convergence rate is proven to be independent of the problem’s condition number in many cases. These findings offer significant improvements on prior asymptotic results and provide a more complete picture of BFGS’s global behavior, offering valuable insights to improve and develop future optimization algorithms.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in optimization because it provides the first non-asymptotic global convergence analysis of the BFGS algorithm, a widely used method, with inexact line search. This closes a significant gap in our understanding and offers new insights into the algorithm’s performance and complexity, paving the way for more efficient and robust optimization methods. It also directly addresses current research trends focusing on global convergence rates, opening new avenues for research on quasi-Newton methods and line search strategies.
Visual Insights#
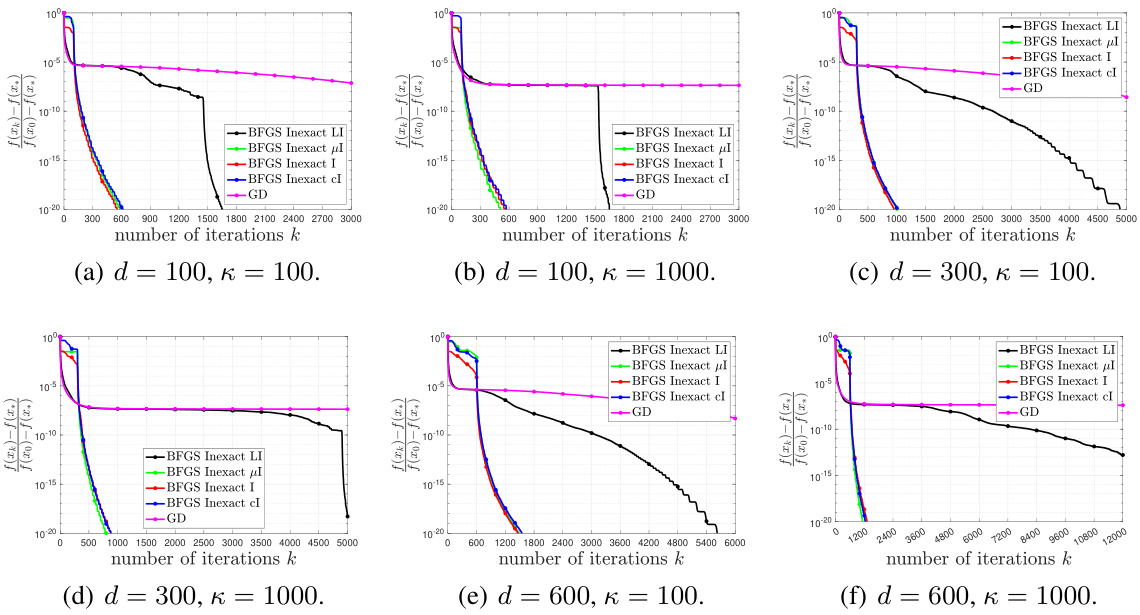
This figure compares the convergence performance of BFGS with inexact line search using different initial Hessian approximation matrices (B0 = LI, B0 = μI, B0 = I, and B0 = cI) against gradient descent with backtracking line search. The x-axis represents the number of iterations, and the y-axis shows the ratio of the function value difference to the initial function value difference. The plots illustrate the convergence behavior across various dimensions (d) and condition numbers (κ). The results suggest that BFGS with B0 = LI converges faster initially, but BFGS with B0 = μI transitions to superlinear convergence sooner.
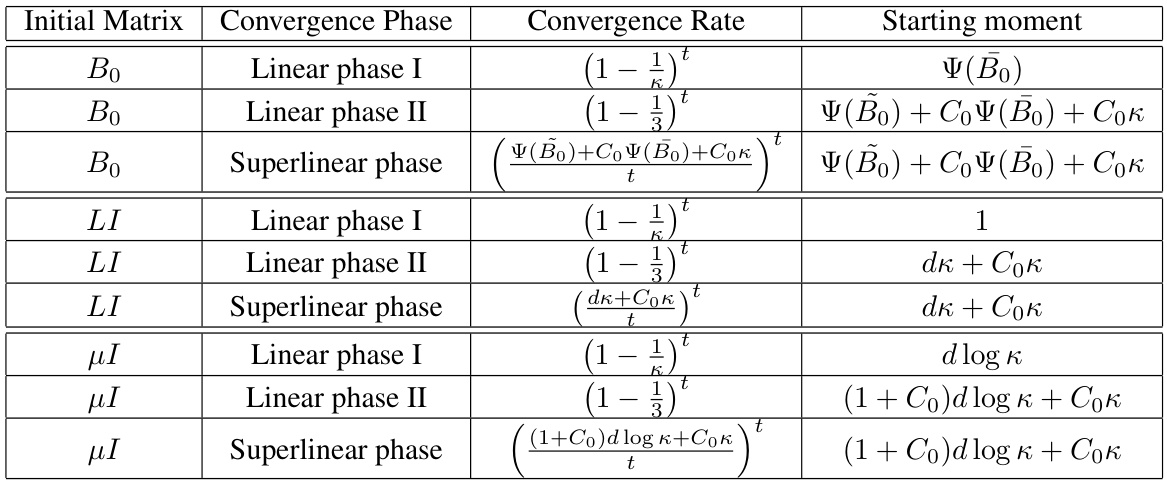
This table summarizes the global convergence rates achieved by the BFGS method with the Armijo-Wolfe line search under different initialization conditions. Three cases are considered: (i) arbitrary positive definite initial Hessian approximation matrix B0, (ii) B0 initialized as the identity matrix scaled by L (B0 = LI), and (iii) B0 initialized as the identity matrix scaled by μ (B0 = μI). For each case, the table shows the convergence rate during the linear phase I, the linear phase II, and the superlinear phase, along with the number of iterations needed to enter each phase. The rates and iteration counts depend on line search parameters, the condition number (κ = L/μ), dimension (d), and the weighted distance (Co) between the starting point and optimal solution. The function Ψ(A) represents a weighted measure of the difference between matrix A and the identity matrix.
Full paper#