Approximation-Aware Bayesian Optimization

↗ OpenReview ↗ NeurIPS Proc. ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial for researchers in Bayesian Optimization (BO) and machine learning, particularly those working with high-dimensional problems. It directly addresses the computational bottleneck in large-scale BO by proposing a novel method that significantly improves efficiency and accuracy. This work opens avenues for scaling BO to even more complex scenarios, which has significant implications across diverse fields.

Visual Insights

#

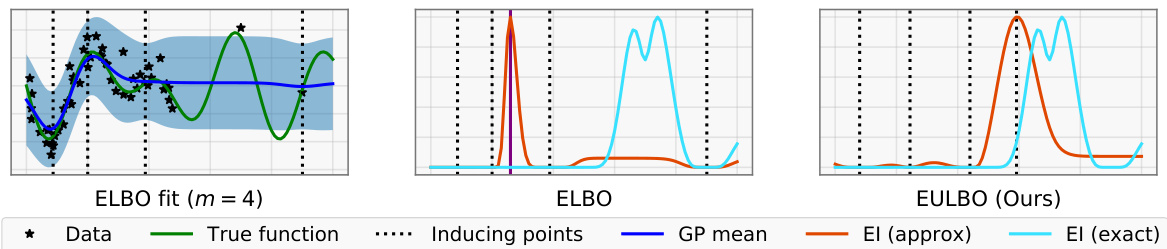
This figure compares three different approaches to Bayesian Optimization using Sparse Variational Gaussian Processes (SVGPs). The left panel shows an SVGP fit with only 4 inducing points, illustrating how the standard ELBO objective focuses only on global data approximation and neglects the downstream decision-making task of selecting the next point with high expected improvement (EI). The middle panel demonstrates that the resulting approximate EI peaks at an incorrect location compared to the exact EI. The right panel illustrates how the proposed utility-calibrated variational inference framework (EULBO) addresses this issue by jointly optimizing the GP approximation and data acquisition, resulting in a candidate selection closer to the exact model.

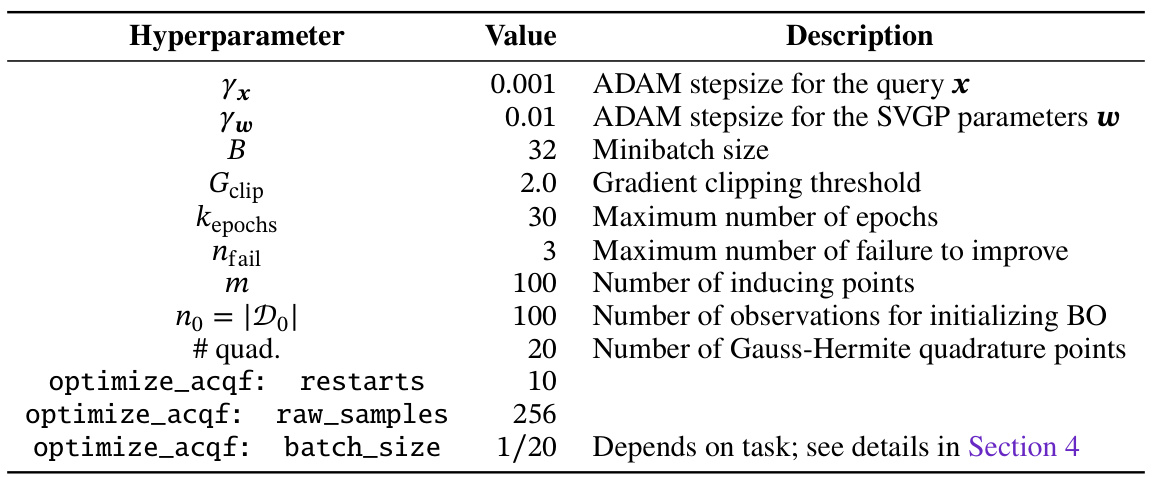
This table lists the hyperparameter settings used in the experiments described in the paper. It includes parameters related to the Adam optimizer (step sizes for query x and SVGP parameters w), minibatch size, gradient clipping, epoch and failure limits for convergence checks, the number of inducing points, initialization data points, quadrature points, and parameters specific to the acquisition function optimization.

In-depth insights

#

Utility-Aware SVGP

#

A Utility-Aware Sparse Variational Gaussian Process (SVGP) framework represents a significant advancement in Bayesian Optimization (BO). Standard SVGPs optimize for global posterior accuracy, which is not the primary goal of BO. A Utility-Aware SVGP directly incorporates the BO acquisition function’s utility into the variational inference process. This joint optimization ensures that the model’s approximation is most accurate in regions relevant to the acquisition function, leading to more informed data acquisition and potentially faster convergence. The key is a novel objective function, possibly an extension of the ELBO (Evidence Lower Bound), that balances posterior fidelity with the expected utility of potential observations. This approach avoids the suboptimal decisions that arise when model approximation and data acquisition are treated as separate problems. The framework’s flexibility allows it to be combined with various acquisition functions (e.g., Expected Improvement, Knowledge Gradient) and batch optimization strategies, demonstrating broad applicability. Efficient computation of the new objective is crucial for scalability, particularly in high-dimensional spaces. This often involves clever approximations or leveraging online update mechanisms to avoid the additional computational burden that joint optimization might introduce.

EULBO Optimization

#

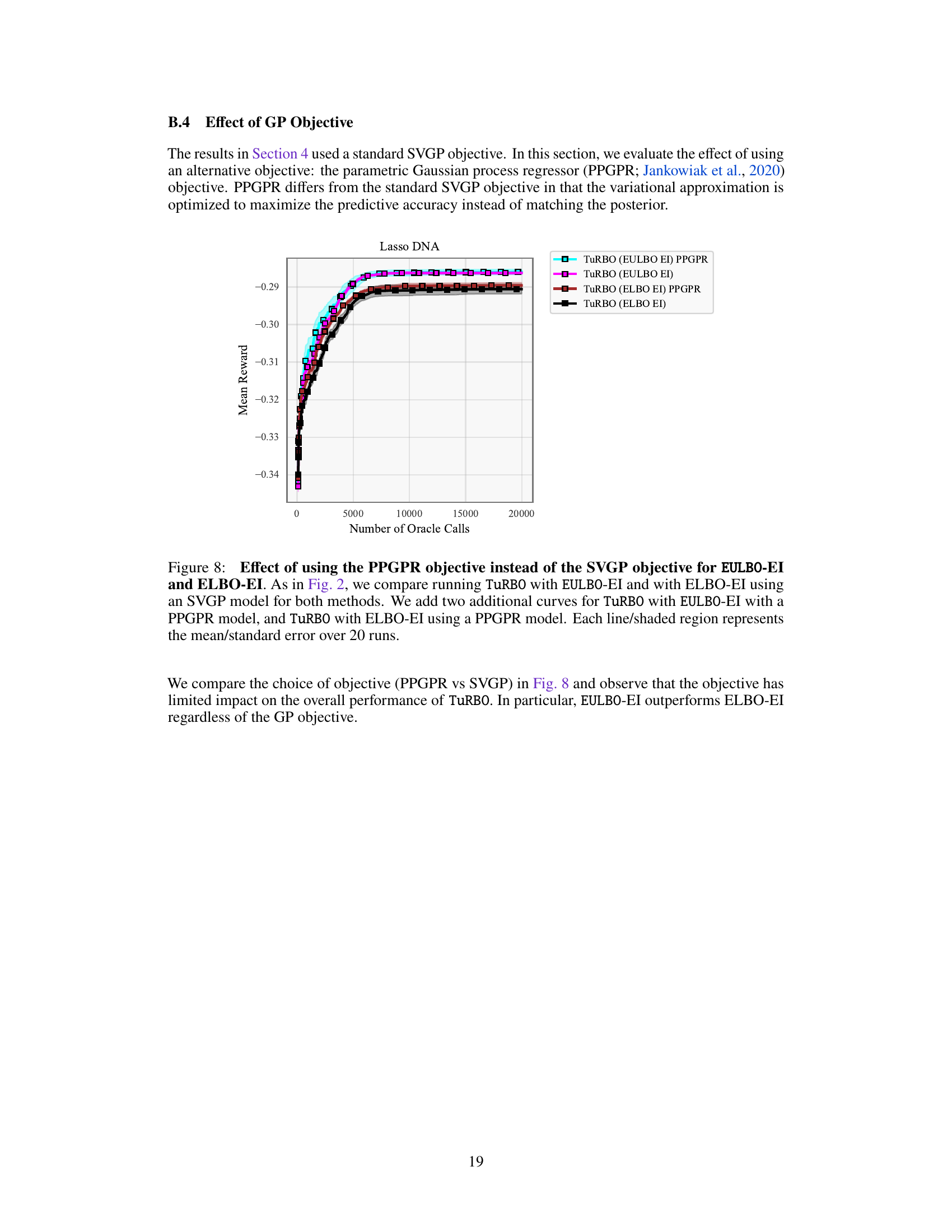
The core of this research paper revolves around a novel approach to Bayesian Optimization (BO) using a modified Sparse Variational Gaussian Process (SVGP). The key innovation is the introduction of the Expected Utility Lower Bound (EULBO), which unifies GP approximation and data acquisition into a single optimization problem. Unlike standard SVGP training that prioritizes global posterior fidelity, EULBO directly optimizes the acquisition function, ensuring data acquisition is guided by the goal of efficient optimization rather than global model accuracy. This is achieved by maximizing a joint objective function that balances posterior accuracy and the expected utility, enabling informed decisions under computational constraints. Efficient optimization strategies are presented for common acquisition functions such as Expected Improvement (EI) and Knowledge Gradient (KG), leveraging recent developments like online variational updates to maintain efficiency. Benchmark results demonstrate that this approach, especially when combined with trust region methods, outperforms standard SVGP methods on high-dimensional optimization problems. The EULBO framework offers a flexible and efficient approach, applicable to various acquisition functions and batch BO scenarios, making it a promising advancement in high-dimensional Bayesian Optimization.

High-Dim BO

#

High-dimensional Bayesian Optimization (High-Dim BO) tackles the challenge of optimizing expensive black-box functions in high-dimensional spaces. This is crucial for real-world applications like materials science and drug discovery, where evaluating a single point is computationally expensive. Traditional BO methods struggle in high dimensions due to the curse of dimensionality. Sparse Variational Gaussian Processes (SVGPs) offer a scalable solution, but their approximations can lead to suboptimal data acquisition. The core issue lies in the mismatch between the SVGP’s objective (global fidelity) and the BO objective (informed data acquisition). Approximation-Aware Bayesian Optimization addresses this by jointly optimizing the approximation and acquisition function, resulting in more efficient and effective optimization. This approach ensures that computational resources are focused on regions with high utility, improving convergence rates and overall performance in complex, high-dimensional problems.

KG Acquisition

#

The Knowledge Gradient (KG) acquisition function, a popular choice in Bayesian Optimization, aims to maximize the expected improvement in the predictive model’s accuracy by strategically selecting the next data point to evaluate. Unlike simpler acquisition functions like Expected Improvement (EI), KG explicitly considers the value of information, assessing how much a new observation might shift the posterior distribution and improve future predictions. This makes KG particularly well-suited for high-dimensional problems where uncertainties are significant and a data-efficient search strategy is crucial. However, KG’s computational cost is considerably higher than EI, especially when dealing with large datasets. The paper explores efficient methods to compute and optimize KG within the framework of sparse variational Gaussian processes (SVGPs), leveraging its decision-theoretic interpretation to ensure optimal data acquisition decisions under computational constraints. The proposed approach, integrating KG optimization directly into the SVGP variational inference process, presents a promising strategy for achieving significant improvements in data efficiency for large-scale Bayesian Optimization tasks.

Scalable BO

#

Scalable Bayesian Optimization (BO) addresses the critical challenge of applying BO to high-dimensional problems with large datasets, where traditional methods become computationally prohibitive. Key strategies for achieving scalability involve approximations to the Gaussian process (GP) model, such as sparse GPs (e.g., SVGP) or variational inference techniques. These methods reduce computational complexity by focusing on a smaller subset of data or inducing points. Another crucial aspect is the design of efficient acquisition functions, which guide the selection of the most informative data points for evaluation. Effective acquisition functions in scalable BO often balance exploration and exploitation while minimizing computational cost. Batch optimization, where multiple data points are evaluated concurrently, is also a common technique to improve efficiency and parallelize the optimization process. Ultimately, successful scalability hinges on the balance between accuracy of the approximation, computational efficiency, and overall optimization performance. The goal is to find the sweet spot where the approximation errors are sufficiently small to retain the benefits of BO but the computation remains tractable.

More visual insights

#

More on figures

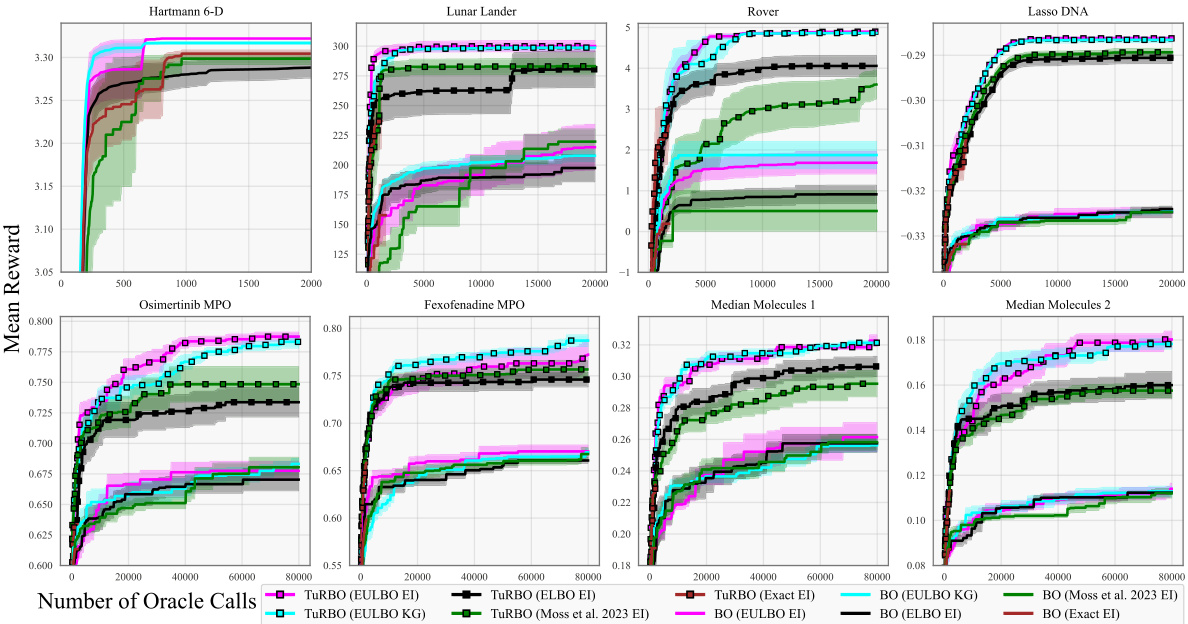
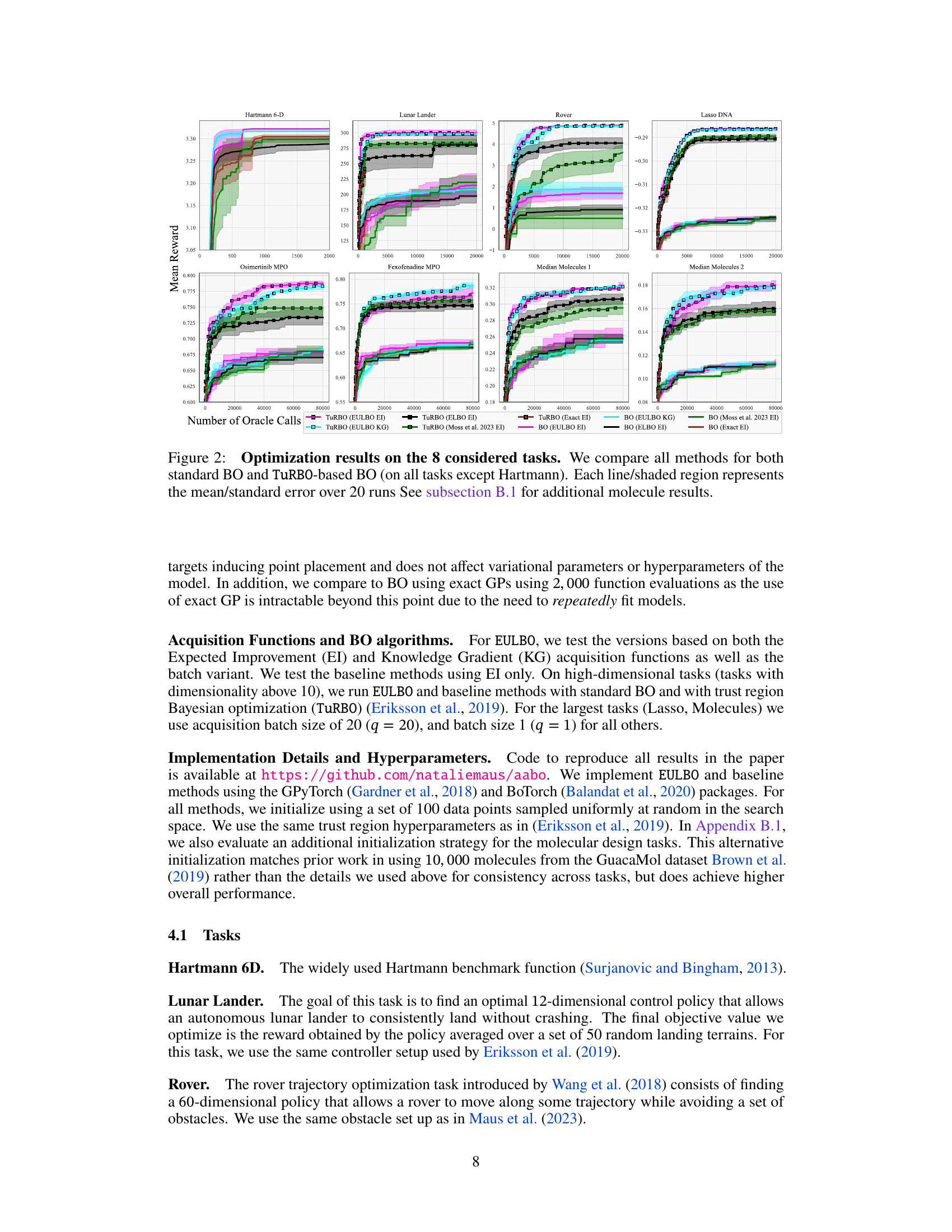
This figure compares the performance of different Bayesian Optimization (BO) algorithms across eight benchmark tasks. The algorithms include standard BO and TuRBO (Trust Region Bayesian Optimization) using various acquisition functions (EI and KG) and different methods for approximating the posterior distribution (ELBO, Moss et al., exact). The plot shows the mean reward achieved versus the number of function evaluations. Shaded areas represent the standard error over 20 independent runs. Additional results for the molecule tasks are provided in the supplementary material.

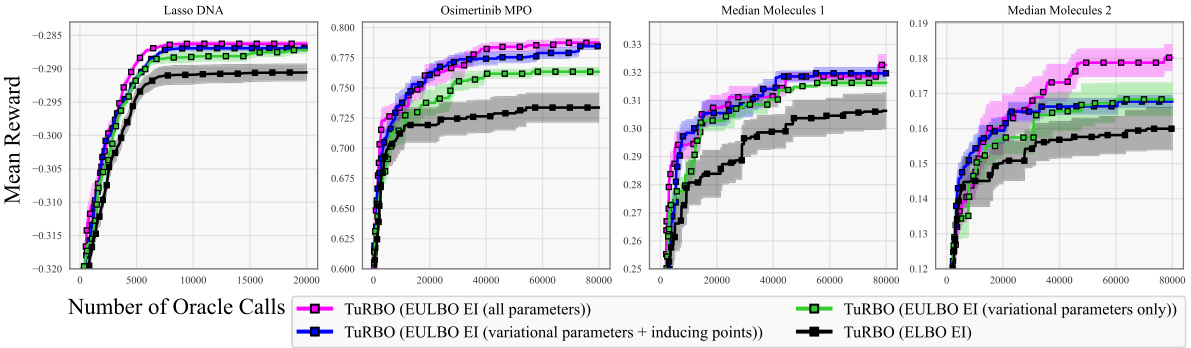
The figure presents optimization results for eight benchmark tasks using different Bayesian Optimization methods. It compares the performance of standard Bayesian optimization (BO) with Trust Region Bayesian Optimization (TuRBO) across four different acquisition functions: EULBO EI (all parameters), EULBO EI (variational parameters + inducing points), EULBO EI (variational parameters only), and ELBO EI. The results illustrate the mean and standard error across 20 runs for each method, highlighting the relative performance of the different approaches on high and low-dimensional problems. Additional results for molecular design tasks are available in subsection B.1.

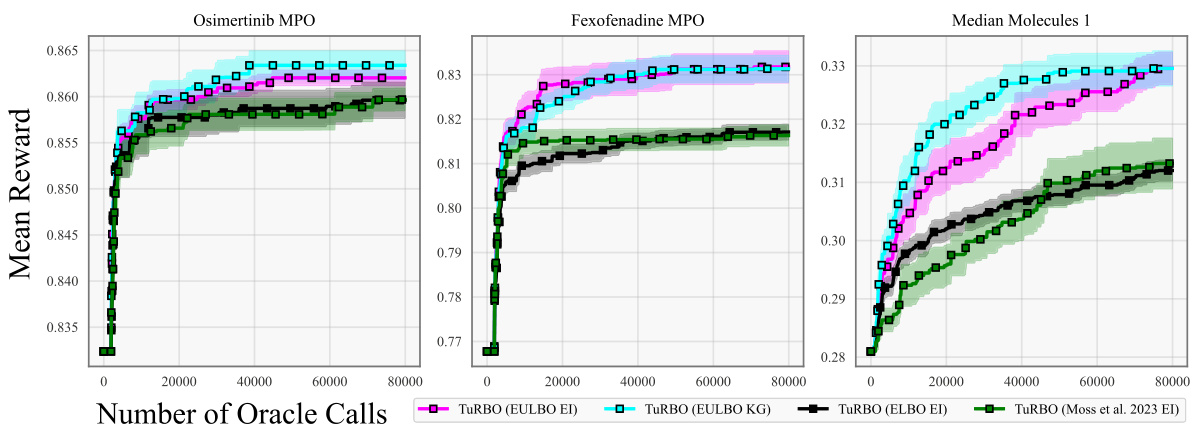
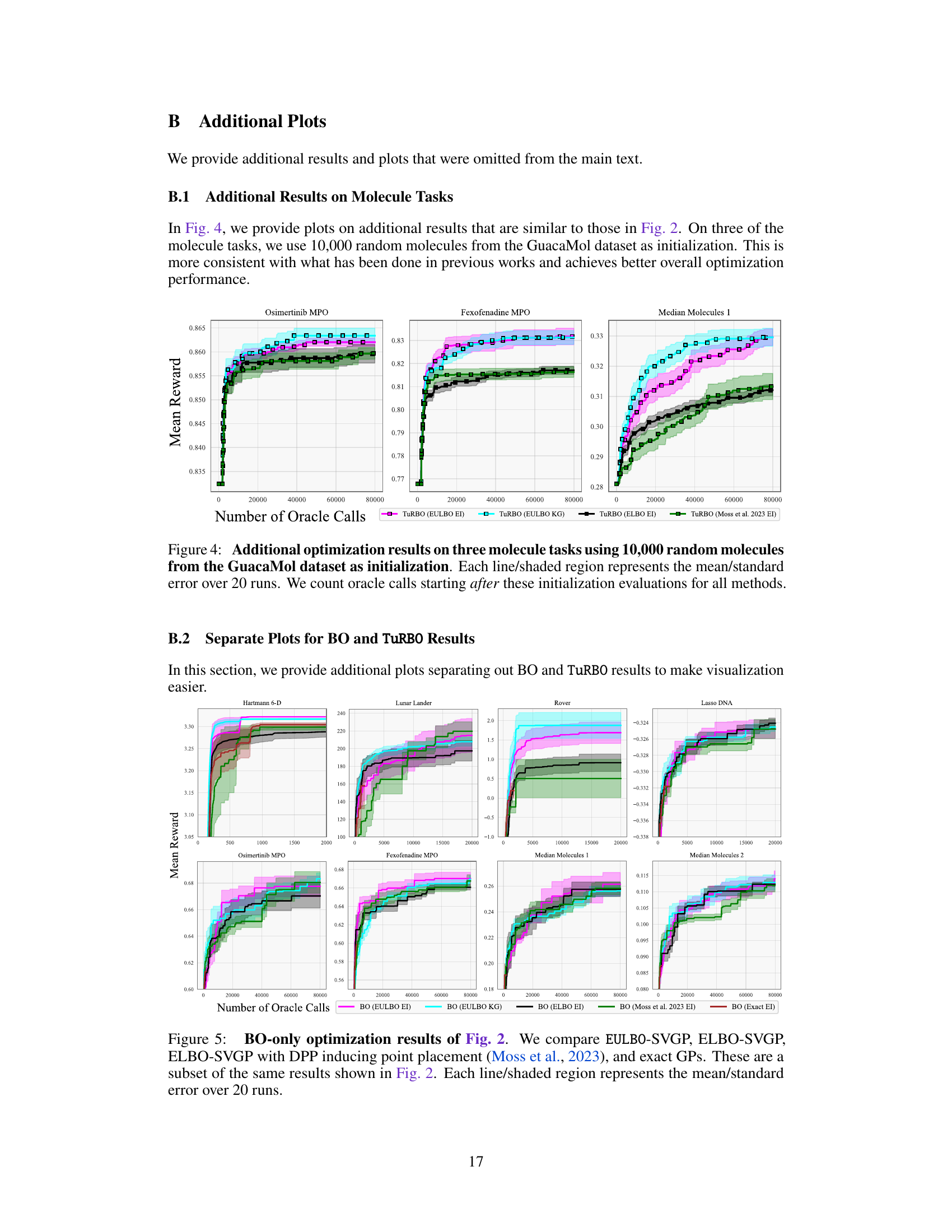
This figure shows the optimization results for three molecule tasks (Osimertinib MPO, Fexofenadine MPO, Median Molecules 1). Unlike Figure 2, these experiments used 10,000 random molecules from the GuacaMol dataset for initialization before starting the optimization process. The plot compares different optimization methods (EULBO EI, EULBO KG, ELBO EI, and Moss et al. 2023 EI) using TuRBO, showing mean reward versus the number of oracle calls (function evaluations). Error bars represent the standard error across 20 runs.

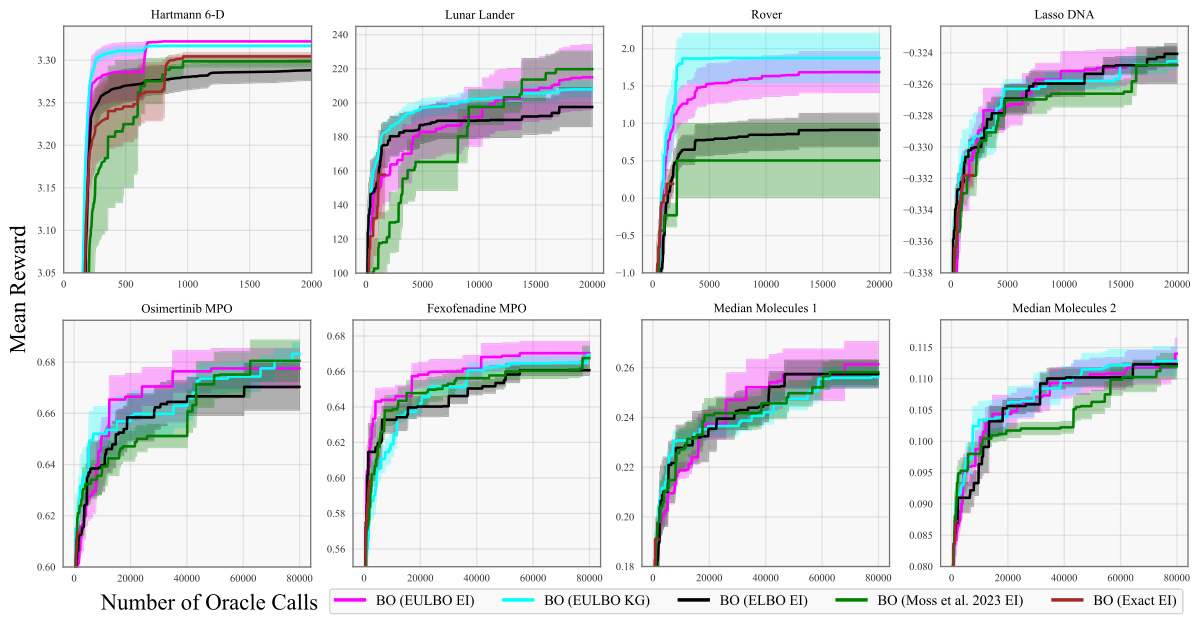
The figure shows optimization results for eight benchmark tasks using various Bayesian optimization methods. The methods compared include EULBO with EI and KG acquisition functions, ELBO with EI, the method from Moss et al. 2023 with EI, and exact EI. Both standard Bayesian optimization and TURBO (Trust Region Bayesian Optimization) are compared. Each line represents the mean reward across 20 runs, with shaded regions showing the standard error. The x-axis represents the number of function evaluations, and the y-axis represents the mean reward. The results show that EULBO generally outperforms the other methods.

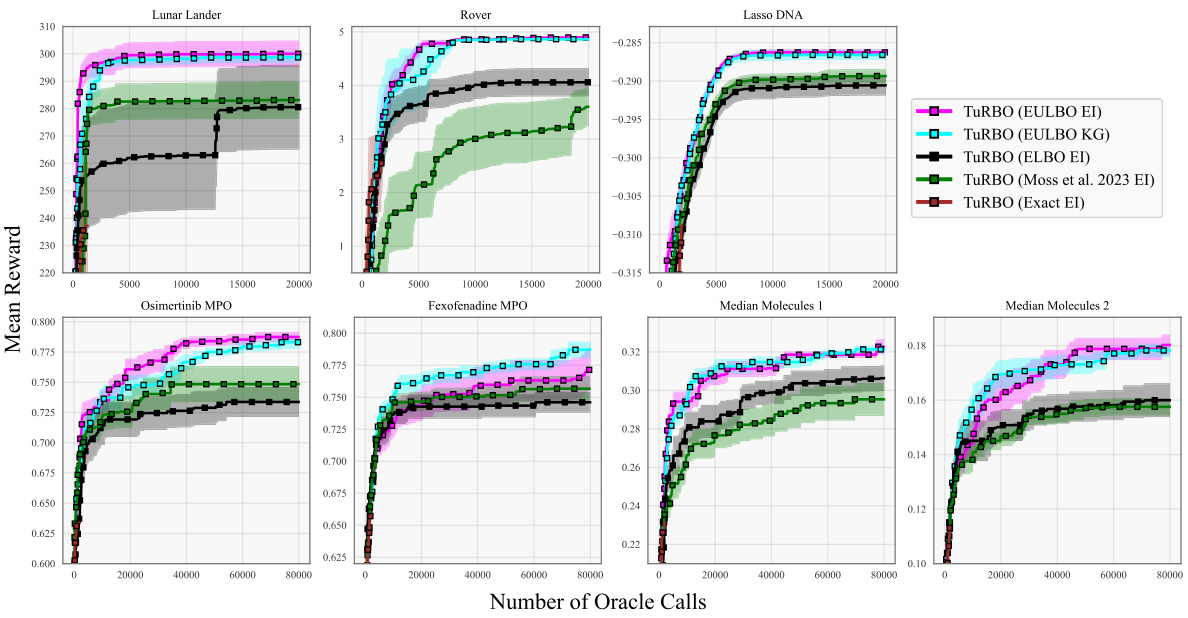
This figure compares the performance of eight different Bayesian Optimization methods across eight benchmark tasks. The methods include variations using standard Bayesian Optimization (BO) and Trust Region Bayesian Optimization (TuRBO). Different acquisition functions (EI and KG) and sparse Gaussian process models (SVGP) with varying approximations are also included. The shaded regions represent the standard error over 20 runs for each method, showing the mean performance of each optimization algorithm.

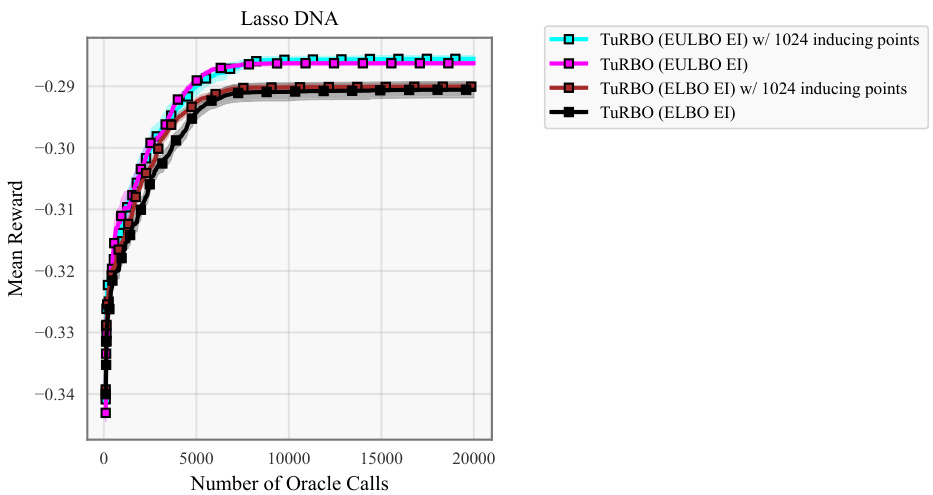
This figure shows the ablation study of the number of inducing points used in the EULBO-SVGP and ELBO-SVGP methods. It compares the performance of TuRBO with both methods using 100 and 1024 inducing points on the Lasso DNA task. The results show that the number of inducing points has a limited impact on the overall performance, and EULBO-SVGP consistently outperforms ELBO-SVGP regardless of the number of inducing points.

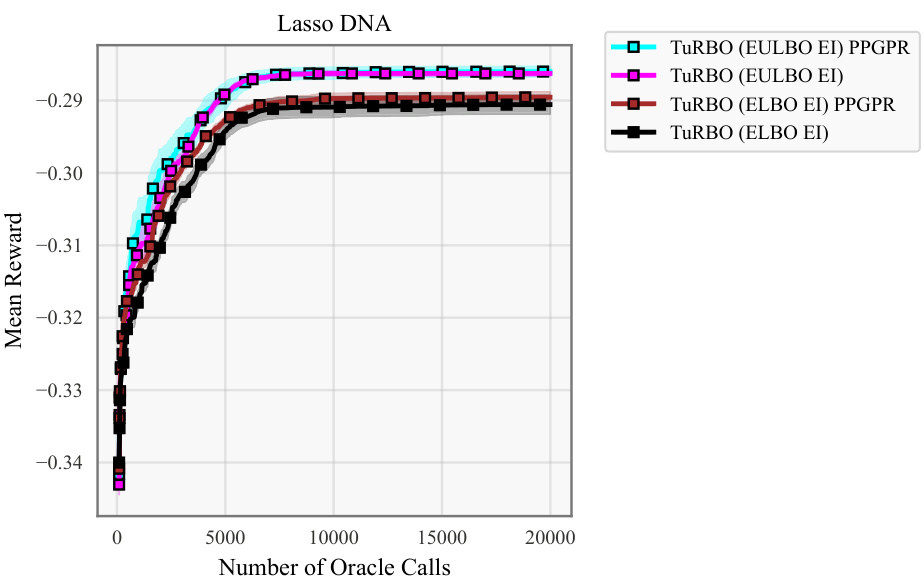
This ablation study investigates the effect of using EULBO optimization on different subsets of SVGP parameters (variational parameters only, inducing points only, or all parameters). It compares the performance of these variations against the standard ELBO approach on four tasks to show the impact of joint optimization on various aspects of the model.

More on tables

This table describes the hardware specifications of the internal cluster used for the majority of the experiments in the paper. It details the system topology (number of nodes, sockets, and logical threads), processor model and clock speed, cache sizes (L1, L2, and L3), total memory (RAM), and the type of accelerator (GPU) used in each node.

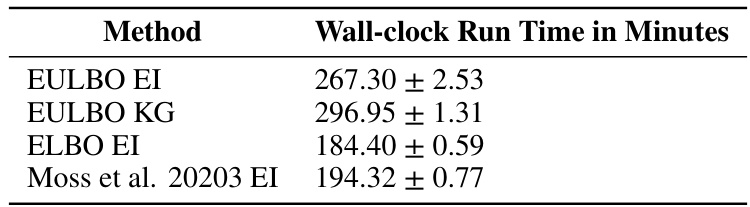
This table shows the average wall-clock run times in minutes for different Bayesian optimization methods on the Lasso DNA task. The methods compared include EULBO EI, EULBO KG, ELBO EI, and Moss et al. 2023 EI, all using TuRBO. The time for the exact EI method is excluded because it was run only to 2000 function evaluations instead of the full 20000.

Full paper

#