↗ OpenReview ↗ NeurIPS Proc. ↗ Chat
TL;DR#
Bayesian deep learning struggles to match the success of standard deep learning due to the high computational cost of estimating full posteriors and the limitations of approximate methods like Laplace approximation. A key issue identified is the lack of reparameterization invariance, where models assign different posterior densities to different parametrizations of the same function. This undermines Bayesian principles and hinders accurate uncertainty quantification.
This research tackles this problem by developing a novel geometric view of reparameterizations. They show that the popular linearized Laplace approximation implicitly handles infinitesimal invariance, and extend this property to the original neural network using a Riemannian diffusion process. This provides a straightforward algorithm for approximate posterior sampling that empirically demonstrates improved posterior fit and predictive performance compared to standard Laplace approximations, significantly mitigating the underfitting issue.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in Bayesian deep learning because it addresses a critical limitation of current approximate posteriors: lack of reparameterization invariance. This work provides a new geometric understanding of this problem, leading to improved posterior sampling methods and potentially more accurate uncertainty quantification in deep neural networks. It opens avenues for developing more robust and reliable Bayesian deep learning models, which is a significant challenge in the field.
Visual Insights#
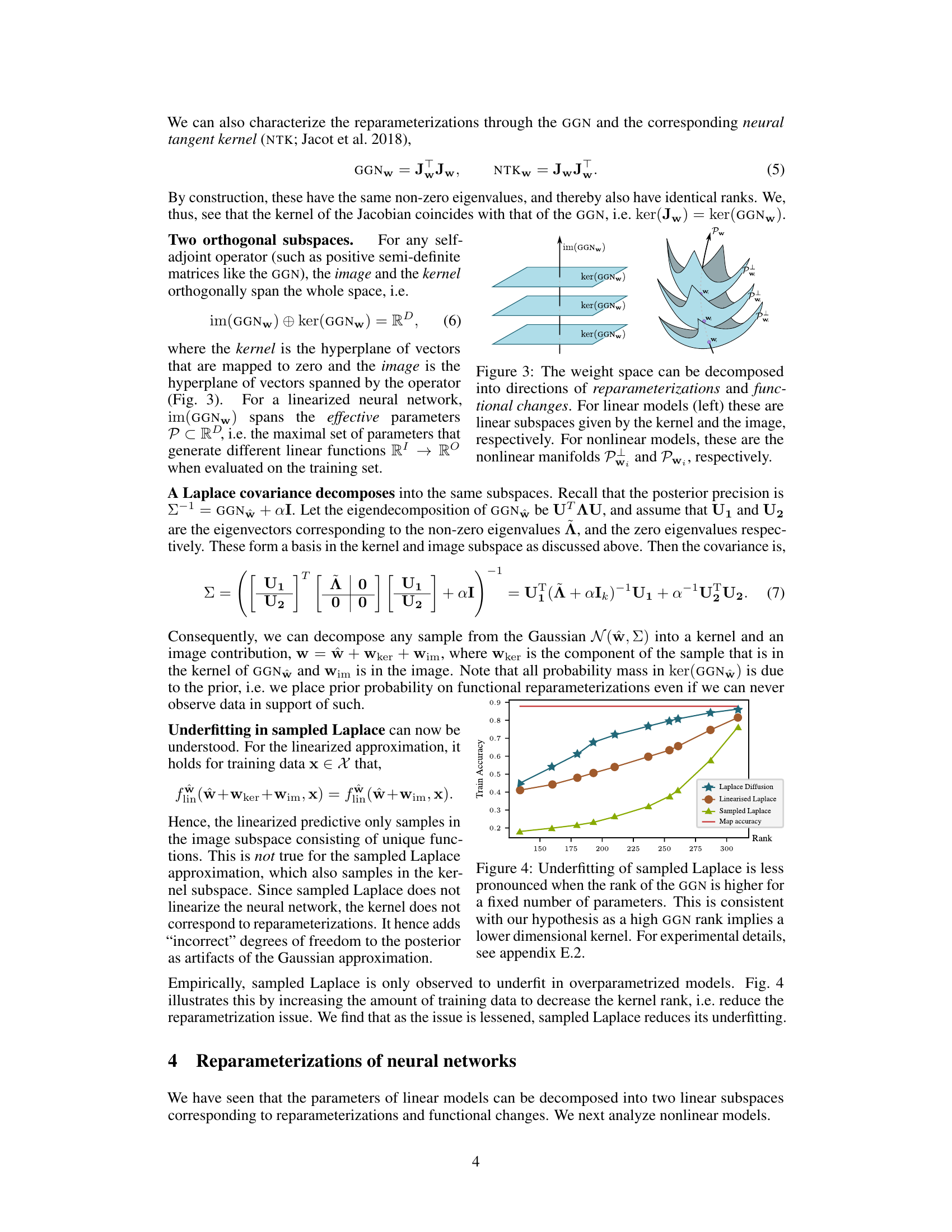
This figure shows how the weight space of a neural network overparametrizes the function space, leading to families of weights corresponding to identical functions. The left panel illustrates how model linearization addresses this issue by linearizing these families. The center panel demonstrates how standard Gaussian weight distributions fail to capture this invariance in nonlinear models. Finally, the right panel showcases how the proposed geometric diffusion method effectively accounts for this invariance by adapting its metric to the families of weights.
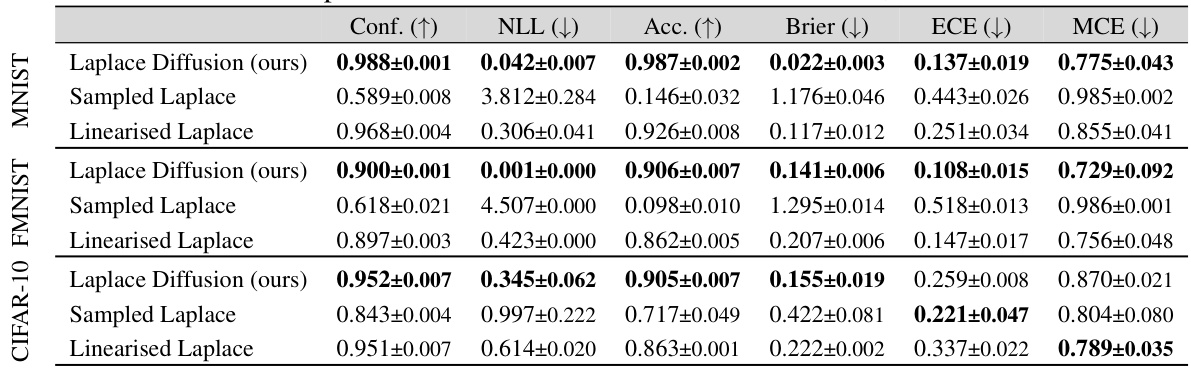
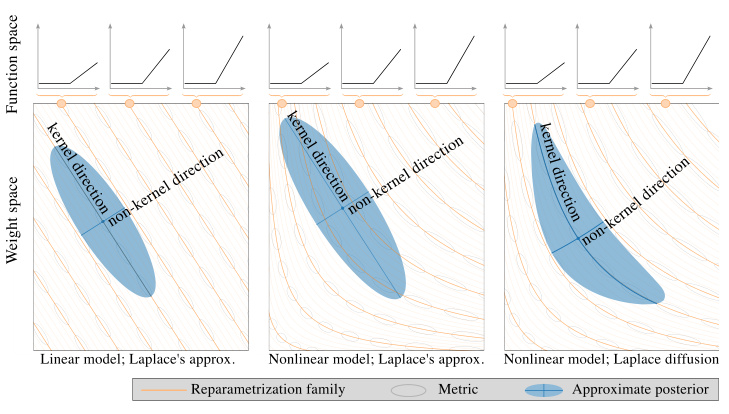
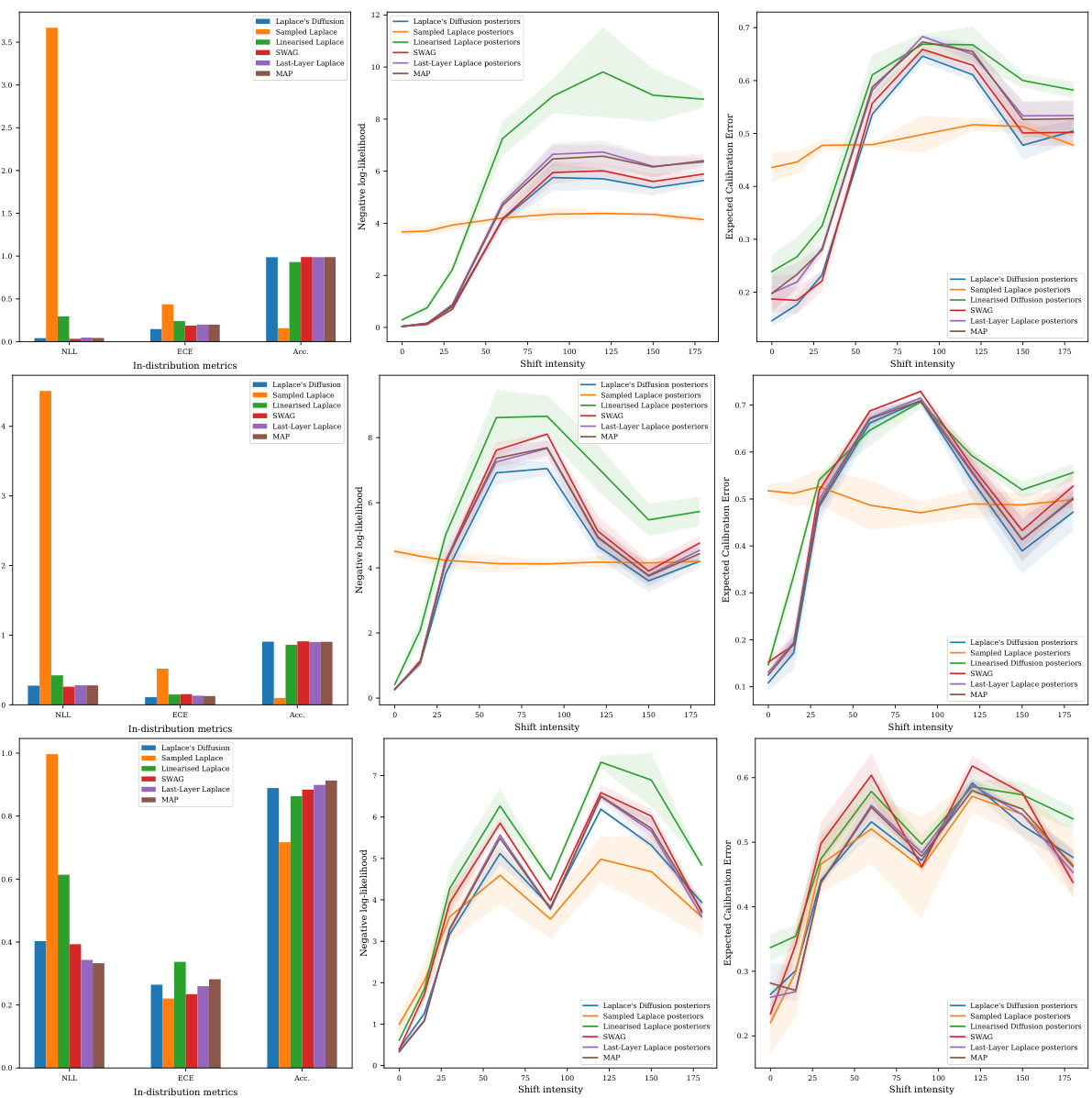
This table presents the in-distribution performance of different Bayesian methods trained on three different datasets: MNIST, FMNIST, and CIFAR-10. The performance is measured using several metrics: Confidence (Conf.), Negative Log-Likelihood (NLL), Accuracy (Acc.), Brier Score (Brier), Expected Calibration Error (ECE), and Maximum Calibration Error (MCE). The table allows for a comparison of the effectiveness of different approaches (Laplace Diffusion, Sampled Laplace, and Linearized Laplace) in terms of their ability to accurately estimate the uncertainty and produce well-calibrated predictions.
In-depth insights#
Reparameterization#
The concept of reparameterization in the context of Bayesian neural networks (BNNs) is crucial because it highlights how different parameterizations of the same function can lead to different posterior distributions. This lack of invariance is a significant limitation of many approximate Bayesian methods, like the Laplace approximation. The paper explores how this issue affects the accuracy and reliability of uncertainty estimates, especially in overparameterized models. The core idea is that handling reparameterizations correctly is vital for building robust and principled BNNs, ensuring consistent uncertainty quantification regardless of the specific parameterization used.
Laplace Diffusion#
The proposed Laplace Diffusion method offers a novel approach to approximate Bayesian inference in deep learning by addressing the limitations of traditional methods like the Laplace approximation. It cleverly leverages the geometric structure of the parameter space, specifically the pseudo-Riemannian manifold induced by the Generalized Gauss-Newton (GGN) matrix, to construct a reparametrization-invariant posterior. Unlike standard methods that suffer from underfitting, particularly in overparametrized models, Laplace Diffusion ensures a better fit by focusing on directions of functional change rather than reparametrizations. The method elegantly integrates into a Riemannian diffusion process which allows for efficient approximate posterior sampling, significantly improving the quality and reliability of uncertainty estimates. Key to its success is the explicit handling of reparameterizations within the weight space, unlike traditional approaches that implicitly ignore this critical aspect. Empirical results demonstrate that Laplace Diffusion consistently outperforms other standard techniques in terms of both in-distribution fit and out-of-distribution detection.
Manifold Geometry#
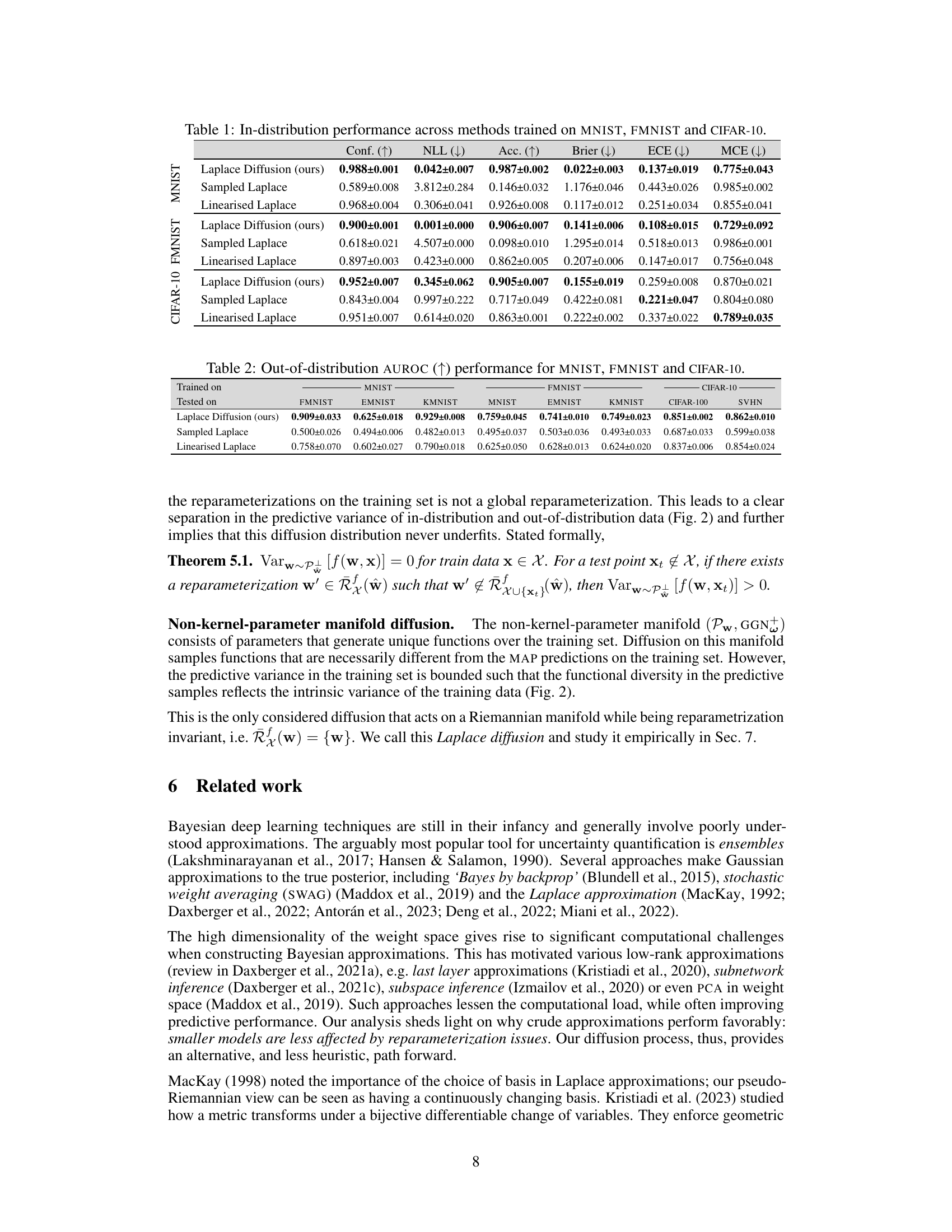
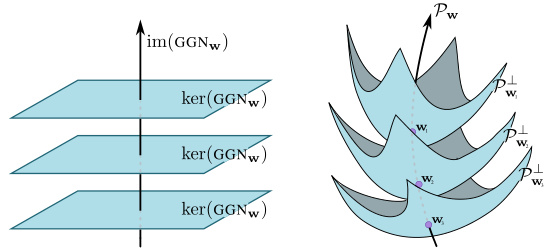
The concept of manifold geometry in the context of Bayesian neural networks offers a powerful framework for understanding and addressing the limitations of traditional methods. Overparameterization in neural networks introduces a redundancy in the representation of functions, leading to non-uniqueness of weight space configurations. By viewing the weight space as a manifold, with its inherent geometric structure, we can define a metric that captures the true uncertainty over functions, rather than just over parameters. This approach is crucial because it accounts for the equivalence classes of weights that represent identical functions, a concept ignored by typical Gaussian approximations. This viewpoint allows for the development of novel inference techniques that are invariant to parameterization choices, leading to improved posterior fits and better out-of-distribution generalization.
Invariant Posterior#
The concept of an “Invariant Posterior” in Bayesian deep learning centers on the ideal that the posterior distribution over model parameters should remain consistent regardless of how the model is parameterized. Current approximate inference methods often fail to achieve this invariance, assigning different posteriors to functionally equivalent models with different parameterizations. This is a critical problem because it violates the fundamental Bayesian principle of representing uncertainty about the function itself, not just the specific parameter values. Achieving parameterization invariance is crucial for reliable uncertainty quantification and model comparison. A key challenge lies in the high dimensionality and non-linearity of neural networks, which makes it difficult to identify and account for all the redundant parameters that contribute to parameterization ambiguity. Therefore, the development of new inference techniques that explicitly address and enforce parameterization invariance is vital for advancing the field of Bayesian deep learning.
Empirical Results#
An empirical results section would thoroughly investigate the proposed Laplace diffusion method’s performance. Key metrics like negative log-likelihood (NLL), accuracy, Brier score, expected calibration error (ECE), and maximum calibration error (MCE) should be reported for in-distribution and out-of-distribution datasets. Crucially, the results should compare Laplace diffusion against standard baselines (e.g., sampled Laplace, linearized Laplace, SWAG) across various datasets (e.g., MNIST, FMNIST, CIFAR-10) to demonstrate its superiority and robustness. A focus on the variance of predictions, particularly in out-of-distribution settings, is needed to highlight the method’s effectiveness in quantifying uncertainty. Furthermore, analysis of the impact of hyperparameter choices (e.g., step size, rank of approximation) on model performance is essential for a complete evaluation. Visualizations like plots showing predictive uncertainties across in-distribution and out-of-distribution data would aid readers’ understanding and provide additional insights.
More visual insights#
More on figures
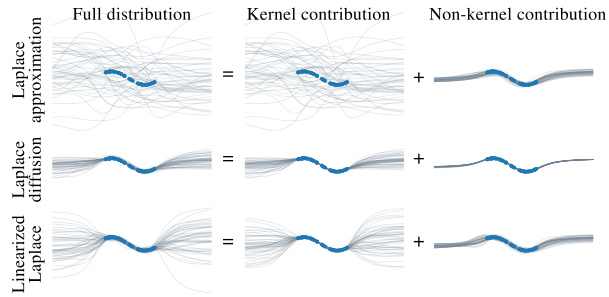
This figure shows the decomposition of the function space into two subspaces: the kernel subspace, representing reparameterizations, and the non-kernel subspace, representing functional changes. The Laplace approximation (top left) underfits because it assigns significant probability mass to the kernel subspace. Linearizing the Laplace approximation (top middle) helps to reduce the underfitting. The Laplace diffusion method (top right) further improves the fit by concentrating the probability mass on the non-kernel subspace. The bottom row shows the kernel and non-kernel contributions separately for each of the three methods.
This figure illustrates the concept of reparameterization invariance in the context of neural networks. The left panel shows that linearizing a neural network collapses families of weights that represent the same function into a single point. The center panel demonstrates that a standard Gaussian distribution over weights fails to capture the redundancy inherent in the overparameterization. The right panel shows that a novel Riemannian diffusion method proposed in this paper addresses this issue by adapting the distribution over weights to the geometry of the function space, better capturing the equivalence between different sets of weights representing the same function.
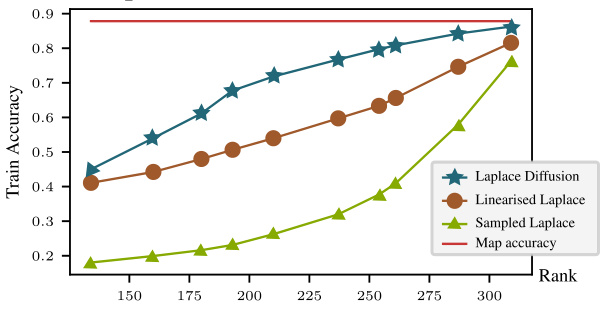
The figure shows the training accuracy for different methods (Laplace Diffusion, Linearised Laplace, and Sampled Laplace) plotted against the rank of the Generalized Gauss-Newton (GGN) matrix. As the rank of the GGN increases (meaning there are fewer redundant parameters), the underfitting problem observed in Sampled Laplace decreases, while Laplace Diffusion shows consistently high accuracy. This supports the paper’s hypothesis that underfitting in Sampled Laplace is due to insufficient handling of reparameterizations, which are linked to the kernel (null space) of the GGN. A higher rank GGN signifies a smaller kernel, leading to less underfitting.
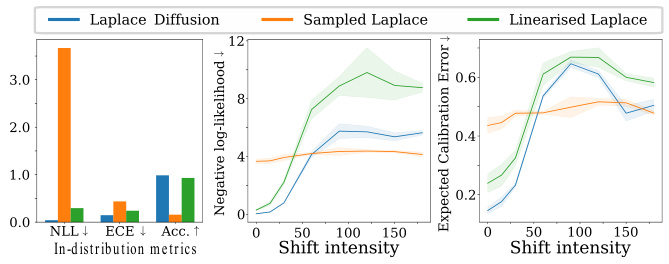
This figure presents benchmark results for Rotated MNIST, comparing the performance of Laplace Diffusion, Sampled Laplace, and Linearised Laplace. It shows that Sampled Laplace severely underfits, even without rotation, while Laplace Diffusion consistently outperforms the other methods across various metrics (NLL, ECE, Accuracy). The results for FMNIST and CIFAR-10 datasets are detailed further in Appendix E.3.2.
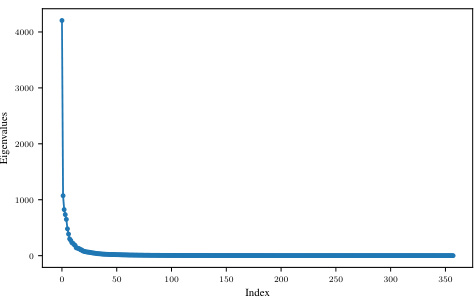
The figure shows the eigenvalues of the Generalized Gauss-Newton (GGN) matrix for a convolutional neural network trained on the MNIST dataset. The eigenvalues are plotted against their index, demonstrating a rapid decay in magnitude. This indicates that a significant portion of the GGN’s information is concentrated in a small number of principal components, suggesting the possibility of low-rank approximations of the GGN for computational efficiency.
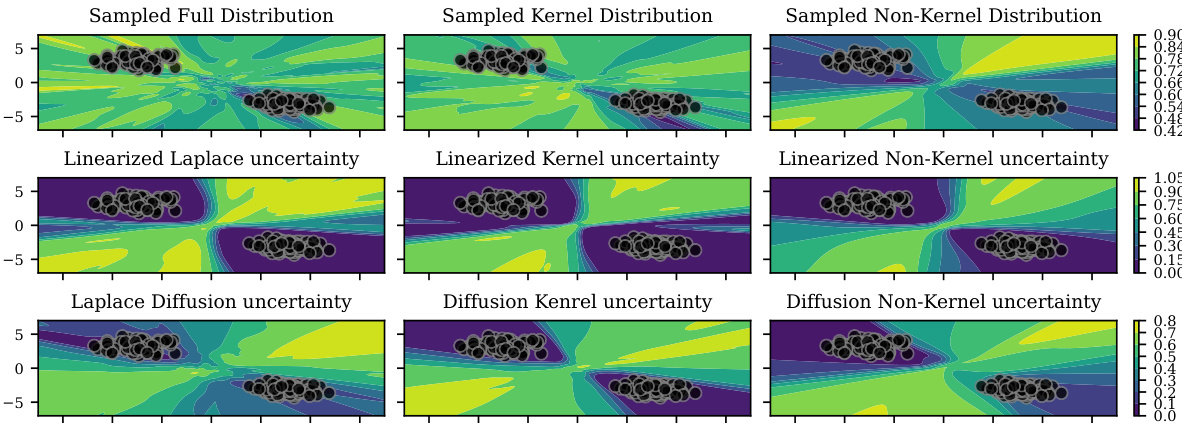
This figure shows a comparison of uncertainty estimations from three different Bayesian approximation methods: Sampled Laplace, Linearized Laplace, and Laplace Diffusion. Each method is evaluated based on its full uncertainty, kernel uncertainty, and non-kernel uncertainty. The results are visualized as contour plots, showing how the different methods capture uncertainty in the input space of a Gaussian mixture classification problem. The black dots represent data points from the Gaussian mixture, and the color gradients illustrate the magnitude of uncertainty. The figure helps to explain how the Laplace approximation methods suffer from an underfitting issue, particularly in the non-kernel direction. The Laplace diffusion method is shown to provide a more accurate representation of uncertainty, particularly by capturing the uncertainty in the non-kernel direction more accurately. This underfitting issue in the other approaches is attributed to their insufficient handling of reparameterizations.
This figure illustrates how the weight space of a neural network overparameterizes the function space. In the linear case (left), model linearization effectively linearizes families of weights corresponding to the same function. However, for non-linear models (center, right), the Gaussian weight distributions don’t adapt well to these families. The paper’s proposed geometric diffusion method (right) addresses this issue by incorporating the geometry of the parameter space, thus achieving reparameterization invariance as depicted by the gray ellipses.
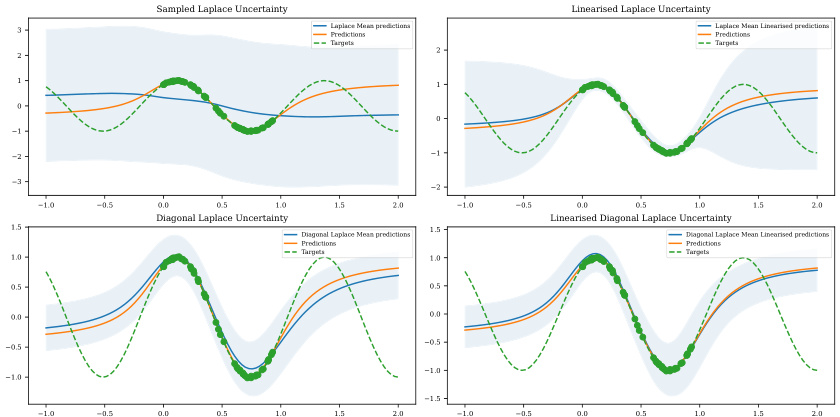
This figure illustrates the concept of reparameterization invariance in the context of Bayesian neural networks. The left panel shows how linearizing a model simplifies the weight space, making different weight settings that represent the same function collapse into single points. The center panel demonstrates how a standard Gaussian distribution in weight space (nonlinear model) fails to capture this invariance, resulting in assigning different posterior densities to different parametrizations of the same function. The right panel shows how the proposed Riemannian diffusion method correctly adapts to this geometry, exhibiting invariance to reparameterizations, and resulting in a posterior that reflects uncertainty over functions rather than parameters.
More on tables

This table presents the out-of-distribution Area Under the Receiver Operating Characteristic curve (AUROC) for several Bayesian deep learning methods. The models were trained on MNIST, FMNIST, and CIFAR-10 datasets and tested on a variety of out-of-distribution datasets to evaluate their ability to generalize to unseen data. The AUROC scores indicate the performance of each method in distinguishing between in-distribution and out-of-distribution samples.
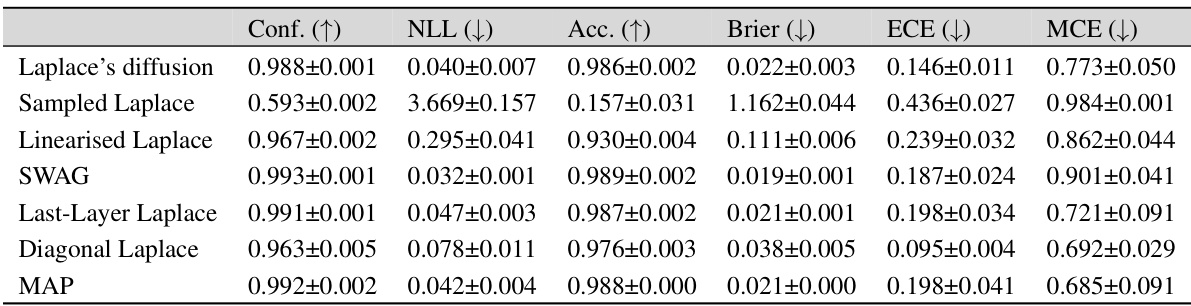
This table presents the in-distribution performance of different Bayesian methods on three benchmark datasets: MNIST, Fashion-MNIST, and CIFAR-10. The performance is evaluated using several metrics: Confidence, Accuracy, Negative Log-Likelihood (NLL), Brier Score, Expected Calibration Error (ECE), and Maximum Calibration Error (MCE). The results show how different methods compare in terms of calibration, accuracy, and predictive uncertainty within the training distribution.
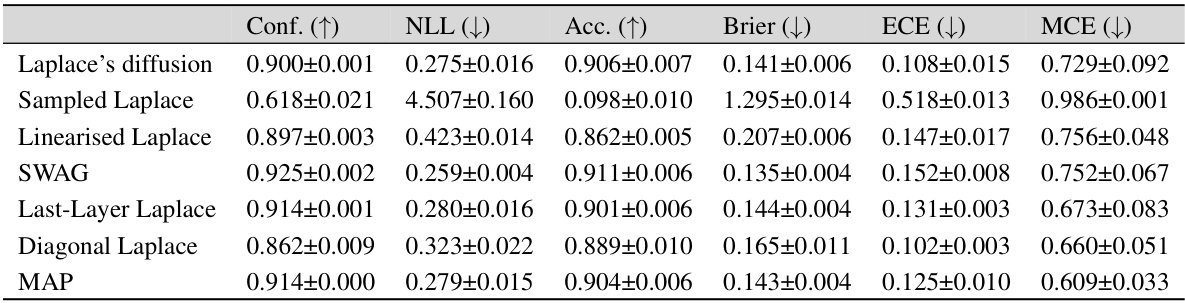
This table presents a comparison of different Bayesian methods (Laplace diffusion, Sampled Laplace, Linearised Laplace, SWAG, Last-Layer Laplace, Diagonal Laplace, and MAP) in terms of their in-distribution performance. The metrics used to evaluate performance include Confidence, Negative Log-Likelihood (NLL), Accuracy (Acc), Brier Score (Brier), Expected Calibration Error (ECE), and Maximum Calibration Error (MCE). The results are shown for three different datasets: MNIST, FMNIST, and CIFAR-10, allowing for a comparison of method performance across various datasets.
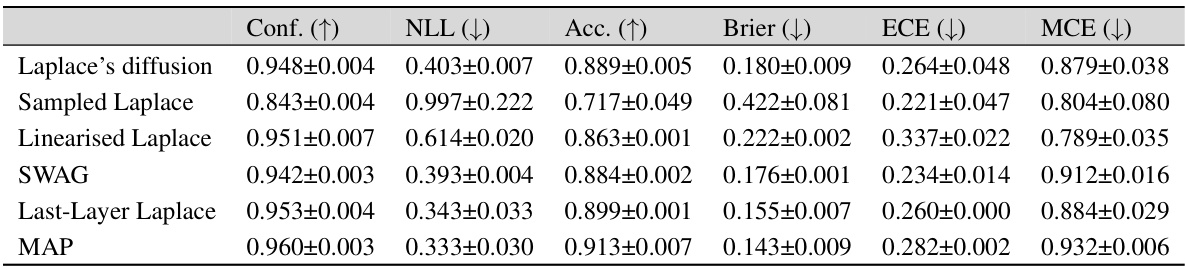
This table presents the in-distribution performance of different Bayesian methods trained on three datasets: MNIST, FMNIST, and CIFAR-10. The performance is evaluated using several metrics: Confidence (Conf.), Negative Log-Likelihood (NLL), Accuracy (Acc.), Brier score (Brier), Expected Calibration Error (ECE), and Maximum Calibration Error (MCE). Lower values are better for NLL, Brier, ECE, and MCE, while higher values are better for Conf. and Acc. The table allows for a comparison of the performance of Laplace Diffusion (the proposed method) against other approaches like Sampled Laplace, Linearised Laplace, etc.
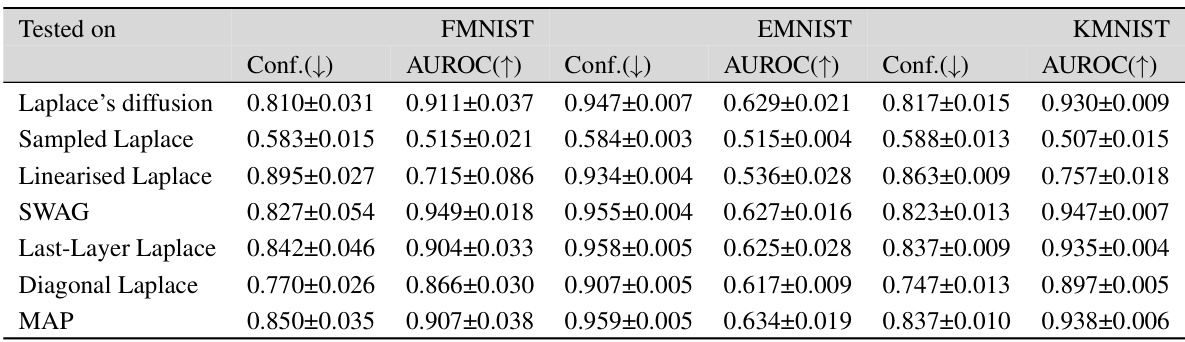
This table presents the out-of-distribution Area Under the Receiver Operating Characteristic curve (AUROC) for different Bayesian methods tested on MNIST, FMNIST, and CIFAR-10 datasets. AUROC is a metric that measures the ability of a classifier to distinguish between in-distribution and out-of-distribution data. Higher AUROC values indicate better performance. The table shows that the proposed Laplace diffusion method generally outperforms other methods in this out-of-distribution setting.
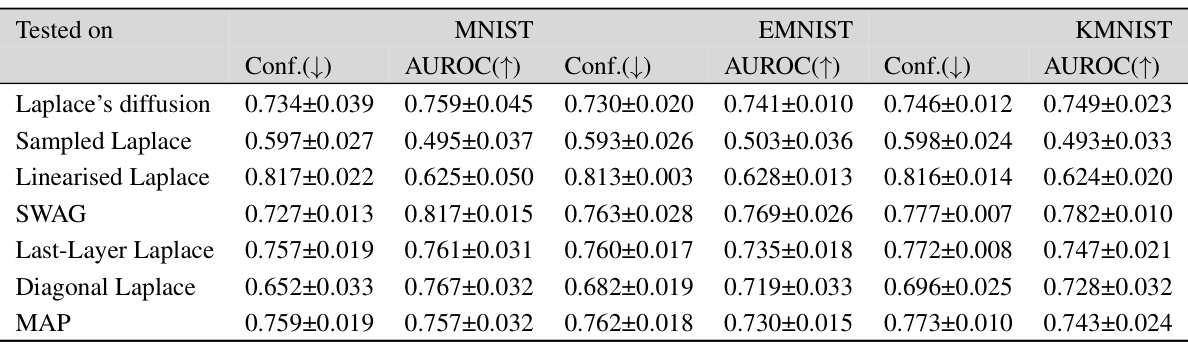
This table presents the out-of-distribution Area Under the Receiver Operating Characteristic curve (AUROC) performance for three different datasets: MNIST, Fashion-MNIST (FMNIST), and CIFAR-10. The AUROC metric is used to evaluate the performance of different methods in distinguishing between in-distribution and out-of-distribution samples. Higher AUROC values are indicative of better performance. The table compares the Laplace diffusion method with other methods, such as sampled Laplace and linearized Laplace.
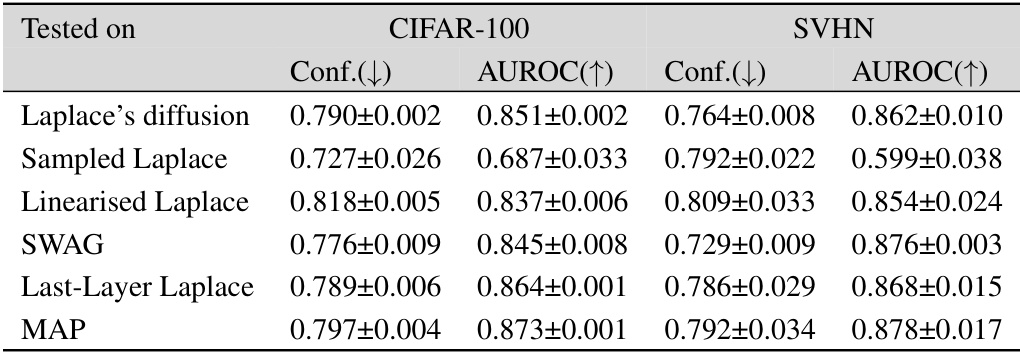
This table presents the results of out-of-distribution AUROC performance using different methods. The AUROC (Area Under the Receiver Operating Characteristic curve) is a metric to evaluate the performance of binary classification. Higher values indicate better performance. The table compares the Laplace diffusion method with sampled Laplace, linearized Laplace, SWAG, last-layer Laplace, diagonal Laplace, and MAP (Maximum a Posteriori) across various out-of-distribution datasets (MNIST, FMNIST, EMNIST, KMNIST, CIFAR-10, CIFAR-100, SVHN). This allows for comparison of the different methods’ ability to generalize beyond the training distribution.
Full paper#