Provable Benefit of Cutout and CutMix for Feature Learning

↗ OpenReview ↗ NeurIPS Proc. ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial because it offers a theoretical understanding of data augmentation techniques like Cutout and CutMix, which are widely used but not well-understood. This provides valuable insights for designing more effective augmentation strategies and advancing feature learning research. The theoretical framework is also highly relevant to current trends in understanding deep learning’s generalization capabilities.

Visual Insights

#

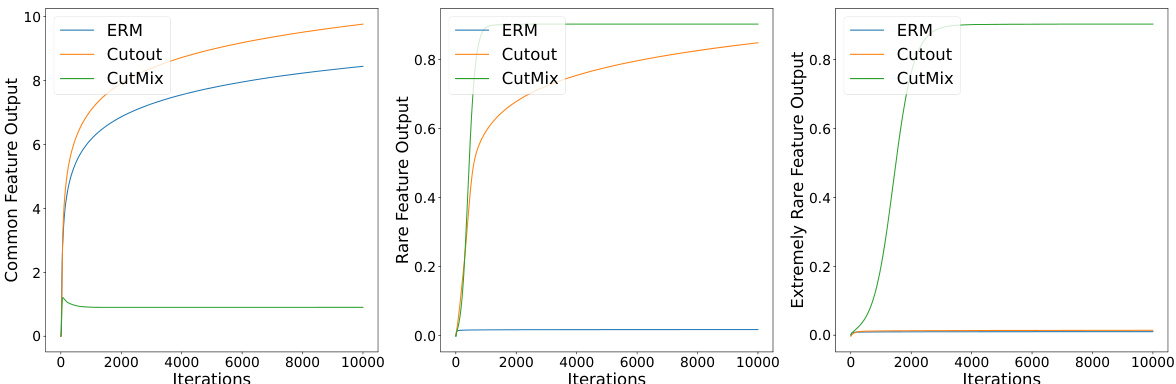
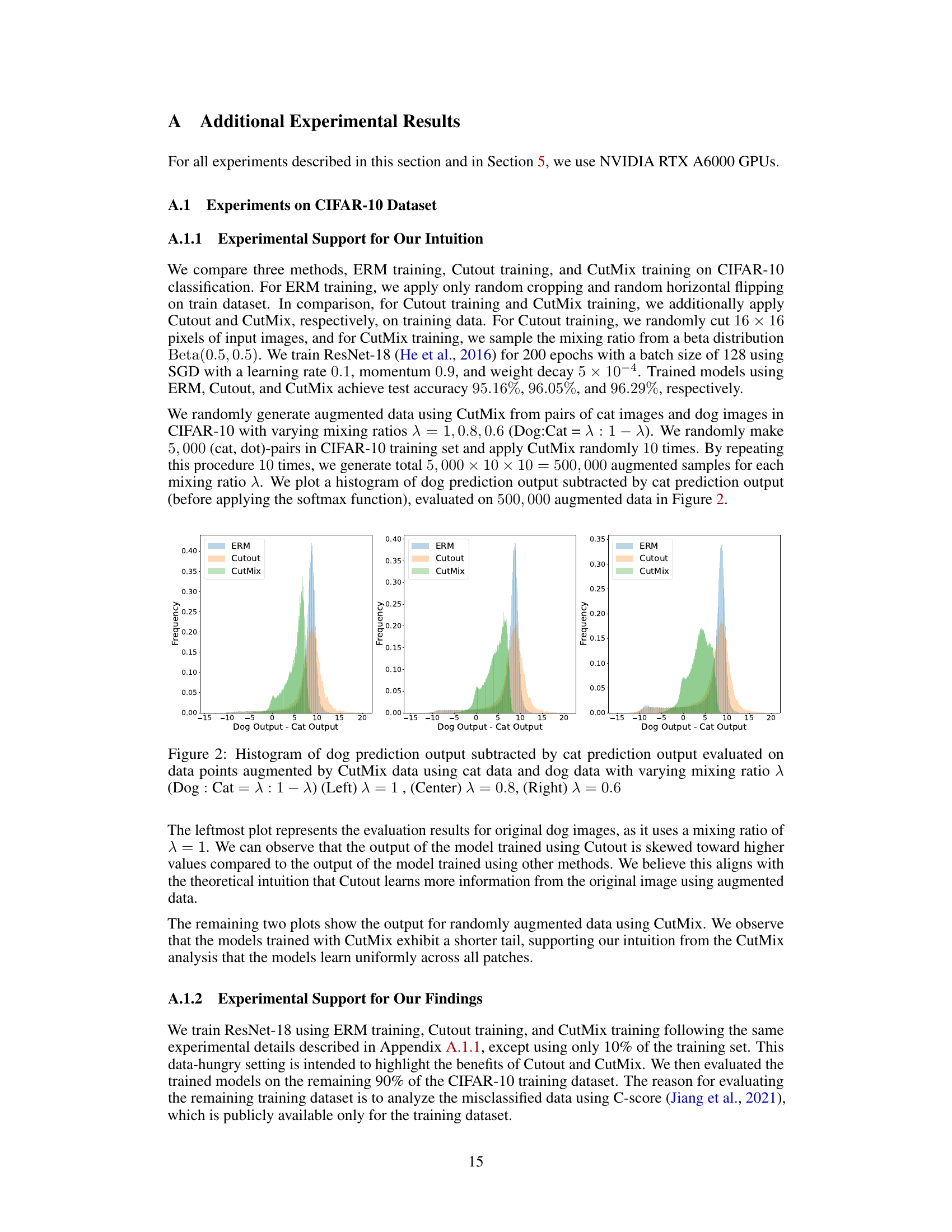
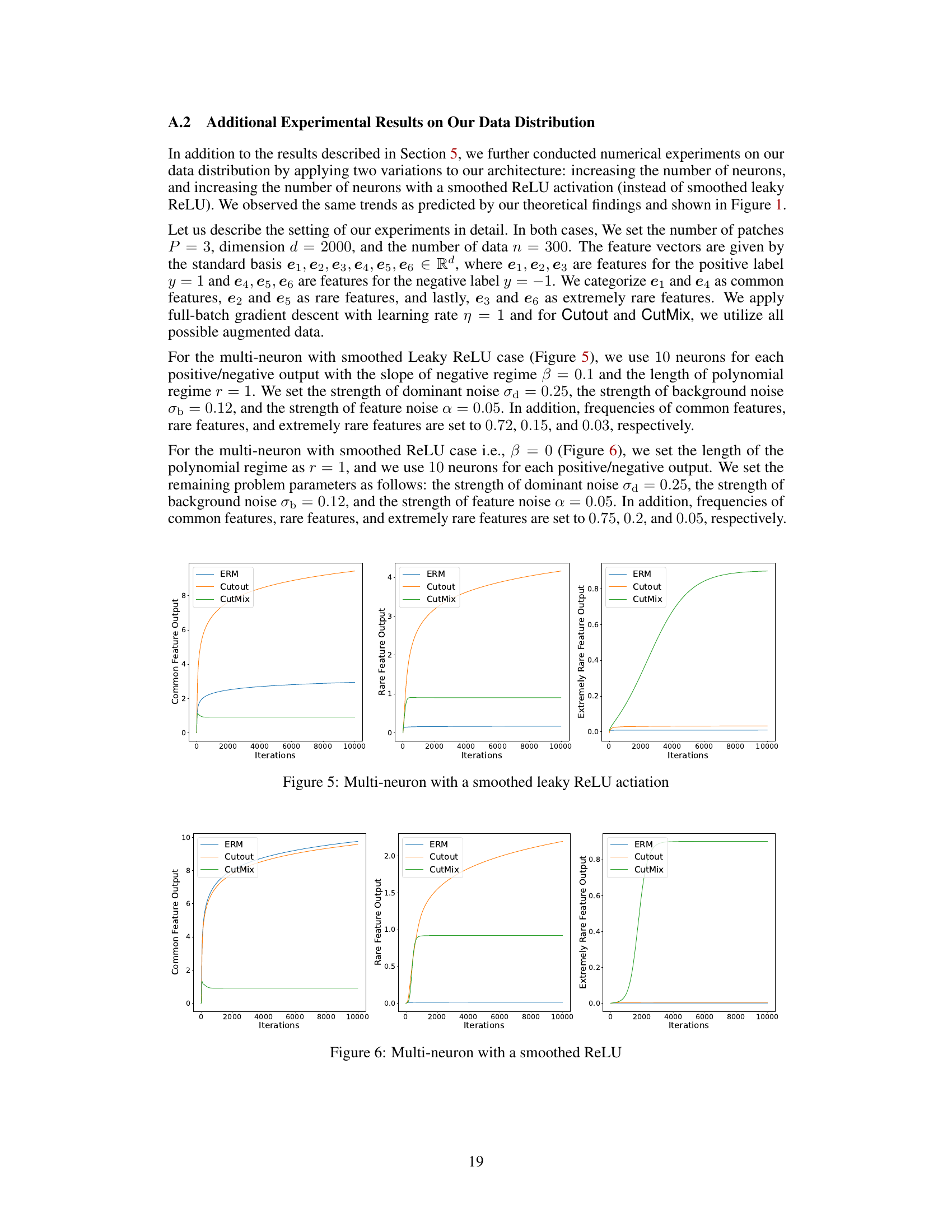
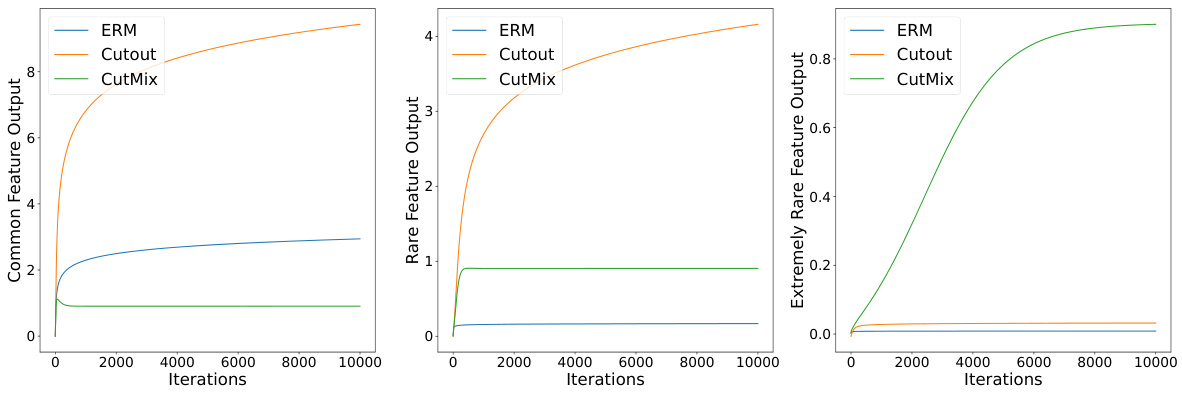
This figure displays the results of numerical experiments conducted to validate the paper’s findings on how different training methods (ERM, Cutout, and CutMix) affect the learning of features with varying frequencies (common, rare, and extremely rare). The x-axis represents the number of training iterations, and the y-axis shows the output of the learned filter for each feature type. The results visually demonstrate that ERM only learns common features, Cutout learns both common and rare features, but fails to learn extremely rare features, whereas CutMix effectively learns all feature types, even exhibiting non-monotonic behavior in learning common features.

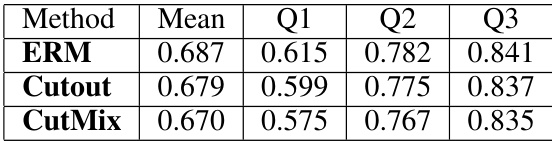
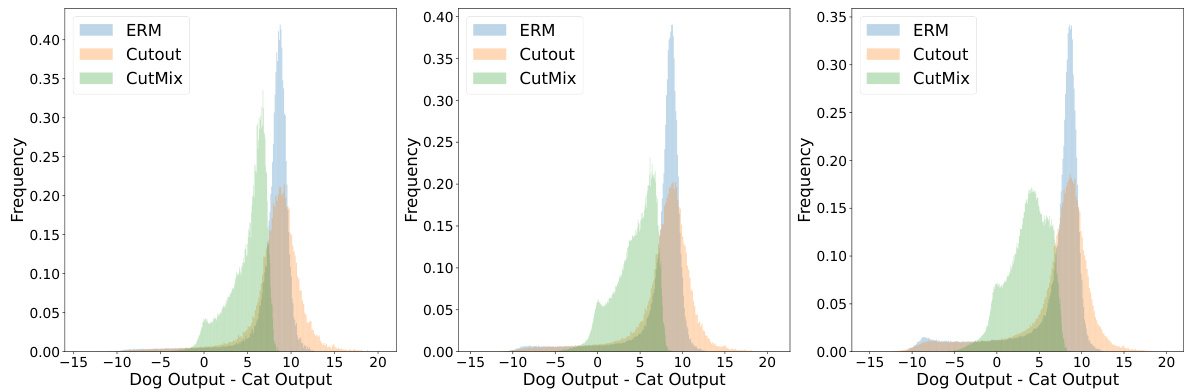
This table presents the mean and quantiles (Q1, Q2, Q3) of C-scores for misclassified data points by three different training methods: ERM, Cutout, and CutMix. The C-score measures how structurally regular the data is, with lower scores indicating more difficult-to-classify examples. The results show that CutMix misclassifies data with consistently lower C-scores, suggesting it learns even the most challenging features. Cutout outperforms ERM, also indicating an improvement in feature learning compared to the baseline.

In-depth insights

#

Cutout/CutMix Theory

#

The Cutout and CutMix data augmentation techniques enhance the performance of deep learning models, particularly in image classification. Cutout randomly removes rectangular regions of an image, while CutMix blends patches from different images, incorporating mixed labels. The theoretical analysis in this paper centers on a two-layer convolutional neural network trained on data consisting of label-dependent features and label-independent noise. This framework reveals that Cutout enables learning of low-frequency features inaccessible to vanilla training, and CutMix expands this further by facilitating the learning of even rarer features. CutMix’s success stems from its ability to make the network activate almost uniformly across all patches, resulting in a more balanced learning of both frequent and rare features. This uniform activation is a critical difference compared to Cutout and standard training methods, providing a theoretical understanding of why CutMix is highly effective.

Feature Learning

#

This research paper delves into the theoretical underpinnings of how data augmentation techniques, specifically Cutout and CutMix, impact feature learning in neural networks. A core finding is that CutMix demonstrates superior performance in learning rare features compared to Cutout and standard training (ERM). The analysis centers around a feature-noise data model that highlights the challenges of learning rare features amidst noise, revealing that Cutout effectively mitigates the effects of strong noise, enabling the learning of rarer features than ERM. However, CutMix goes even further, forcing the model to learn all features and noise vectors with uniform activation, regardless of their rarity or strength. This uniform activation is key to CutMix’s success. The paper’s theoretical framework uses a two-layer convolutional network with a smoothed leaky ReLU activation for analysis, providing valuable insights into the effectiveness of patch-level augmentation strategies.

Data Augmentation

#

Data augmentation is a crucial technique in deep learning, particularly for image data, enhancing model robustness and generalization. Traditional methods involve geometric transformations (rotation, flipping, cropping) and color adjustments. However, patch-level augmentation techniques like Cutout and CutMix have shown superior performance. Cutout randomly masks image regions, forcing the network to learn more robust features, while CutMix blends patches from different images with mixed labels, creating synthetic training samples. The paper focuses on a theoretical analysis of these techniques, demonstrating that Cutout enables learning of low-frequency features that standard training misses, and CutMix goes further by facilitating the learning of even rarer, high-frequency features. This is achieved by analyzing the training process on a specific feature-noise data model. The theoretical findings are supported by empirical results, illustrating the considerable benefits of these patch-level methods. Further research could explore the impact of patch location information, and the extension of these ideas to other data modalities and more complex network architectures.

Two-Layer CNNs

#

The choice of a two-layer convolutional neural network (CNN) in this research is a deliberate design decision, meriting a deeper examination. This architecture, while simple, offers advantages in theoretical analysis. The reduced complexity facilitates a rigorous mathematical treatment, allowing the authors to derive provable guarantees on the network’s ability to learn features under different training regimes. The simplicity allows for a clearer focus on the effects of data augmentation techniques, such as Cutout and CutMix, without being obscured by the intricacies of a deep network’s many layers and parameters. The use of a two-layer CNN strengthens the theoretical results, making them more robust and interpretable. However, this choice introduces a limitation: the findings might not directly generalize to more complex, deep CNN architectures which are commonly used in practical applications. Further research is needed to investigate the extent to which these theoretical insights translate to deeper networks. The use of a two-layer CNN is thus a trade-off: it facilitates a strong theoretical foundation while limiting the direct applicability of the results to real-world, high-performance deep learning models. Despite this limitation, the core insights about feature learning and the effectiveness of Cutout and CutMix remain valuable and contribute significantly to the understanding of data augmentation methods.

Future Work

#

The paper’s exploration of Cutout and CutMix offers a strong foundation for future research. Extending the theoretical analysis to deeper and wider networks with more complex activation functions is crucial. This would provide a more comprehensive understanding of the techniques’ effectiveness in various real-world scenarios. Investigating the interaction between patch-level augmentation and other data augmentation techniques (e.g., geometric transformations, Mixup) would yield valuable insights into optimal data augmentation strategies. Exploring the impact of different masking strategies (shape, size, and distribution) within Cutout and CutMix would also be insightful. Furthermore, a detailed theoretical investigation into the recent variants of Cutout and CutMix, such as Puzzle Mix and Co-Mixup, is necessary to understand their enhanced performance and how they address some of Cutout and CutMix’s limitations. Finally, applying the theoretical framework to other data modalities, beyond images, like text and time-series data, will broaden the applicability and significance of the findings.

More visual insights

#

More on figures

This figure shows the results of numerical experiments conducted to validate the theoretical findings presented in the paper. Three different training methods are compared: Empirical Risk Minimization (ERM), Cutout, and CutMix. Each subplot displays the output of learned filters for a specific type of feature (common, rare, extremely rare) across training iterations. The x-axis represents the training iterations, and the y-axis represents the filter output. The plots illustrate that ERM only learns common features, Cutout learns common and rare features but not extremely rare features, and CutMix learns all types of features relatively evenly. The non-monotonic behavior of the CutMix results for the common feature highlights a key difference between CutMix and the other methods.

This figure shows the results of numerical experiments on a synthetic dataset. Three training methods are compared: Empirical Risk Minimization (ERM), Cutout, and CutMix. The plots track the learned filter outputs for common, rare, and extremely rare features over training iterations. The key takeaway is that CutMix learns all feature types relatively evenly, unlike ERM and Cutout which struggle with rarer features; CutMix also exhibits non-monotonic behavior.

This figure shows the results of numerical experiments on a synthetic dataset designed to test the effectiveness of ERM, Cutout, and CutMix in learning features with varying frequencies. The x-axis represents the number of training iterations, and the y-axis represents the output value of a neuron in the trained network responding to specific feature vectors. The three subplots correspond to common, rare, and extremely rare features, respectively. The results visually demonstrate CutMix’s superior ability to learn even the rarest features, while ERM struggles to learn rare features and Cutout’s performance lies in between. The non-monotonic behavior observed in the CutMix plot for common features highlights the complex dynamics of this training method.

This figure displays the results of numerical experiments conducted to validate the theoretical findings of the paper. Three different training methods were compared: vanilla training (ERM), Cutout, and CutMix. Each method’s performance is shown in learning three types of features: common, rare, and extremely rare. The plots illustrate the output values of the learned filters for each feature type over training iterations. The x-axis represents the number of training iterations, and the y-axis represents the output of the learned filters for each feature type. The results show that ERM only learns common features, Cutout learns both common and rare features, but not extremely rare features. CutMix learns all three types of features almost uniformly. Note that the CutMix method shows non-monotonic behavior, which is a key characteristic investigated in the paper.

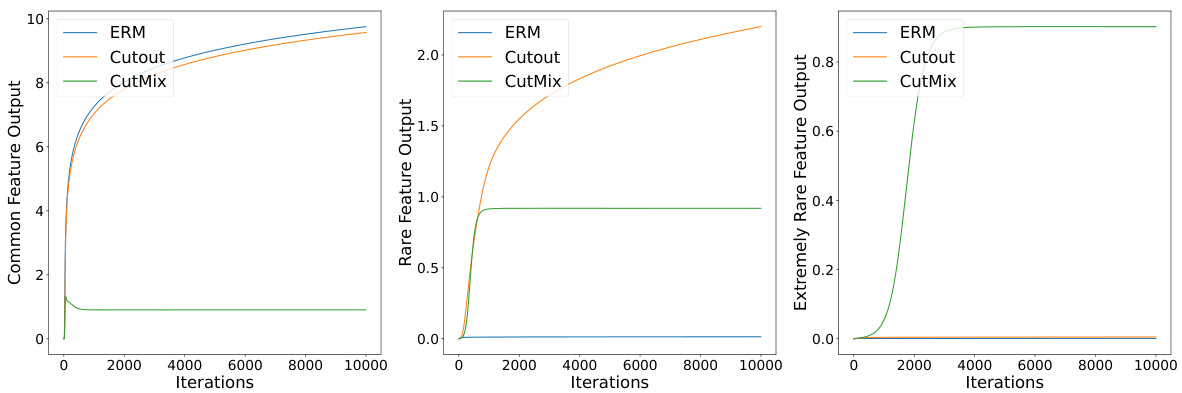
This figure presents the numerical results obtained from the experiments conducted on the proposed feature-noise data model. The left panel shows the learning trend for the common feature, the center panel shows the learning trend for the rare feature, and the right panel shows the learning trend for the extremely rare feature. Each panel displays the output of the feature obtained by three different training methods: ERM (Empirical Risk Minimization), Cutout, and CutMix. The results visually confirm the theoretical findings, that is, ERM can only learn common features, Cutout can learn common and rare features, but not extremely rare features, and CutMix can learn all types of features. The non-monotonic behavior of the common features trained by CutMix is also noticeable. This non-monotonic behavior is a key observation motivating the novel proof techniques introduced in the paper.

Full paper

#