↗ OpenReview ↗ NeurIPS Proc. ↗ Chat
TL;DR#
Traditional latent dynamical systems in neuroscience struggle to capture the distinct roles of different cell types (e.g., excitatory and inhibitory neurons) in shaping neural activity and behavior. This limitation hinders our understanding of brain function and our ability to predict the effects of cell-specific interventions. This paper tackles this challenge by introducing a novel approach that considers multiple cell types in a systematic manner.
The proposed Cell-Type Dynamical Systems (CTDS) model extends existing latent linear dynamical systems by incorporating separate latent variables for each cell type and imposing biologically-inspired constraints. Applied to rat brain recordings during decision-making, CTDS outperforms standard models in prediction accuracy and reveals that choice information is encoded in both excitatory and inhibitory neuron populations. Importantly, CTDS accurately simulates the effects of optogenetic perturbations, offering insights into cell-type specific roles. The model also showcases promise in inferring the types of unknown neurons directly from experimental data, thereby enhancing our ability to perform detailed analyses of the neural circuits.
Key Takeaways#
Why does it matter?#
This paper is crucial for neuroscience researchers because it introduces a novel Cell-Type Dynamical Systems (CTDS) model that significantly improves the accuracy and biological interpretability of neural population dynamics. CTDS addresses the limitations of traditional models by incorporating distinct latent variables for different cell types, leading to better predictions of neural activity and behavioral responses to specific perturbations. This opens exciting new avenues for studying the causal roles of distinct neural populations in brain functions and behavior. Furthermore, its capacity to infer cell types from experimental data makes it a powerful tool for future neurophysiological research.
Visual Insights#
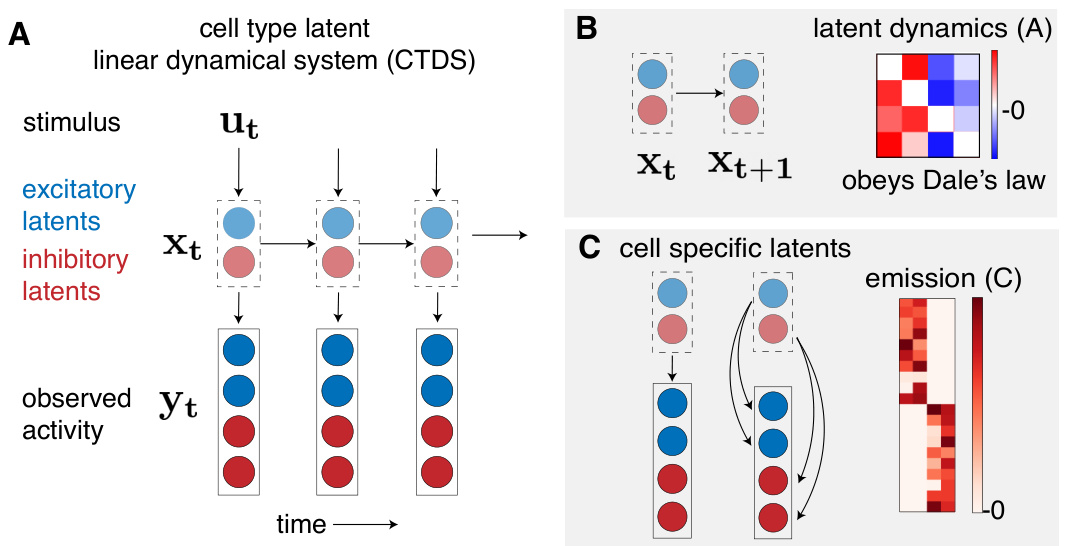
This figure is a graphical model showing the structure of the Cell-Type Dynamical System (CTDS) model. Panel A shows the overall model structure with inputs (stimulus), latent variables for excitatory and inhibitory neurons, and outputs (observed activity). Panel B details the latent dynamics matrix (A) which is constrained to obey Dale’s Law (excitatory neurons have positive weights, inhibitory neurons have negative weights). Panel C shows how the cell-specific latent variables are mapped to the observed neuronal activity via an emission matrix (C) which also has non-negativity constraints.
In-depth insights#
CTDS Model#
The Cell-Type Dynamical Systems (CTDS) model offers a significant advancement in neural population dynamics modeling by explicitly incorporating distinct cell types. Unlike traditional latent dynamical systems that treat all neurons homogeneously, CTDS distinguishes between excitatory and inhibitory neurons, assigning separate latent variables to each. This crucial distinction allows for a more biologically accurate representation of neural activity, capturing the unique roles and interactions of different cell classes. The model’s constraints, such as Dale’s Law for dynamics and non-negativity for emissions, further enhance its biological plausibility and interpretability. CTDS’s ability to accurately predict the effects of cell-specific perturbations, as demonstrated through in-silico optogenetic experiments, highlights its potential for causal inference in neural circuits. Furthermore, its capacity to infer cell types from electrophysiological data with unknown labels adds practical value to neuroscience research. In essence, CTDS provides a more refined and biologically grounded approach to understanding neural population dynamics and their relationship to behavior.
In-silico Perturbations#
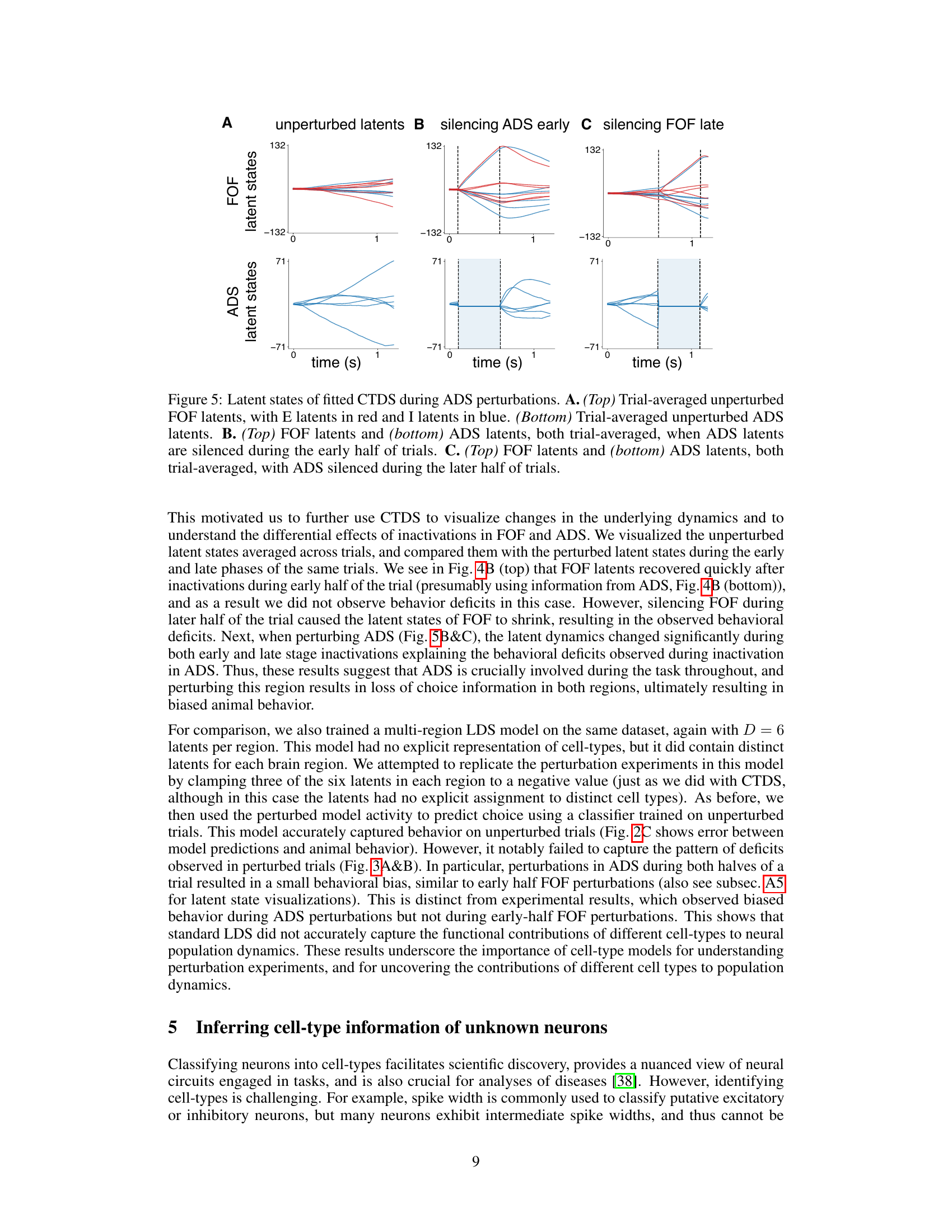
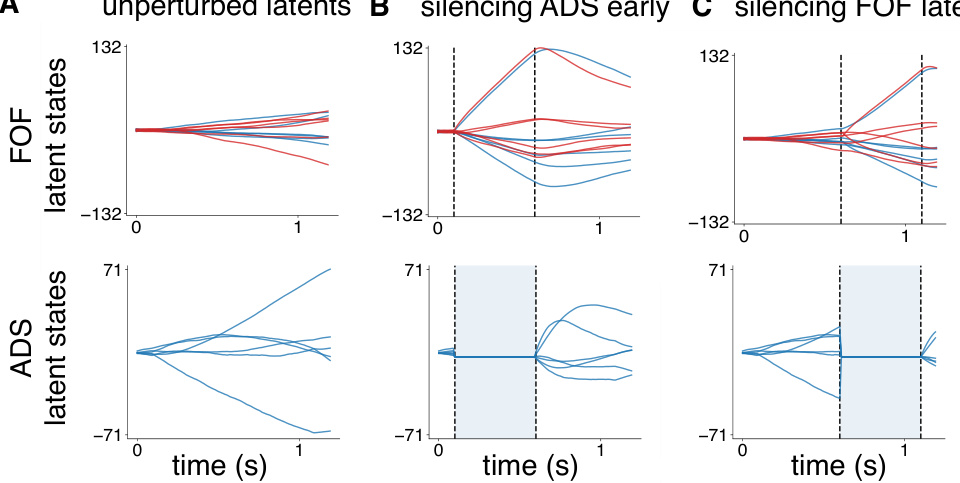
The concept of “in-silico perturbations” within the context of a neuroscience research paper refers to computational experiments simulating the effects of experimental manipulations on neural activity and behavior. Instead of directly perturbing brain regions (e.g., through optogenetics), researchers use a computational model of the neural system to mimic these perturbations. This allows for a more efficient and less invasive way to study causal relationships between neural activity and behavior. Specifically, by selectively modifying parameters within the model, researchers can isolate and analyze the effects of specific cell types or brain regions. This approach is especially valuable when studying complex systems like the brain where direct manipulation is difficult. The results from in-silico experiments offer valuable predictions, which can subsequently be tested with real biological experiments. This iterative process of in-silico exploration and biological validation helps refine both models and experimental designs, leading to a more comprehensive understanding of neural circuitry.
E-I RNN Equivalence#
The E-I RNN equivalence section likely explores the mathematical relationship between the Cell-Type Dynamical System (CTDS) model and a recurrent neural network (RNN) with excitatory (E) and inhibitory (I) units. The core idea is to show that under specific conditions, a low-rank E-I RNN is mathematically equivalent to a CTDS. This equivalence is crucial because it bridges two different modeling approaches: the biologically-inspired CTDS and the computationally-flexible E-I RNN. Demonstrating this equivalence would provide theoretical validation for the CTDS, highlighting that the constraints and assumptions it imposes are not arbitrary but naturally arise from the dynamics of E-I neural circuits. The analysis probably involves matrix factorizations and constraints on the signs of connection weights to satisfy Dale’s Law (E cells only excite, I cells only inhibit). Successful demonstration of this equivalence would strengthen the CTDS model’s applicability and provide insights into how to effectively design and interpret E-I RNNs for tasks related to neural population dynamics and behavior.
Cell-Type Inference#
Cell-type inference, in the context of neural population dynamics, presents a significant challenge and opportunity. Accurately identifying the cell type of individual neurons is crucial for understanding neural circuit function, as different cell types (e.g., excitatory and inhibitory neurons) play distinct computational roles. Traditional methods, such as spike width analysis, often lack accuracy and suffer from limitations. The development of computational methods that can infer cell type from neural activity data alone would be a significant advancement, particularly for large-scale neural recordings where manual cell-type identification is impractical. One such approach is to leverage the dynamics of neural activity, potentially using models such as Cell-Type Dynamical Systems (CTDS) which can incorporate biologically inspired constraints to improve accuracy. Successfully integrating these methods with experimental perturbation techniques would allow a direct link between computational modeling and causal inferences regarding the function of different cell types. The accuracy and limitations of any such inference method must be carefully evaluated, and further research should focus on developing robust and efficient algorithms, particularly for cases with high noise levels and incomplete data.
Future Directions#
Future research could explore extending the Cell-Type Dynamical Systems (CTDS) model to nonlinear dynamics, enhancing its capacity to capture the intricate complexity of neural interactions. This would involve investigating various nonlinear model structures and assessing their performance in fitting and predicting neural activity. Another promising avenue is to expand the CTDS framework to encompass more diverse cell types beyond simple excitatory and inhibitory classifications. Incorporating diverse cell types, including interneurons with different physiological properties, would facilitate the modeling of more complex neural circuits and their roles in behavior. Furthermore, the development of methods for efficiently inferring cell-type information from electrophysiological recordings without prior knowledge would greatly advance CTDS’s practical utility. This involves improving algorithms to accurately classify neurons and handle ambiguities in spike width and other features. Finally, a key focus should be on applying the CTDS model to a wider range of neural systems and tasks. Investigating its capacity to model complex behaviors in different brain regions and understanding how cell type interactions contribute to different behavioral outputs would unveil valuable insights into neural computation and information processing.
More visual insights#
More on figures
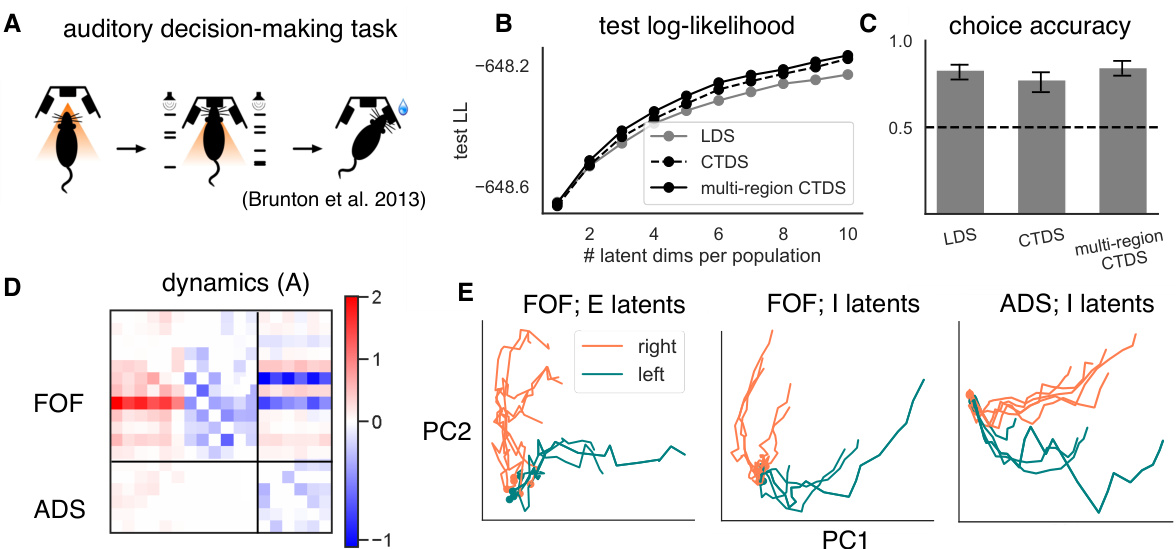
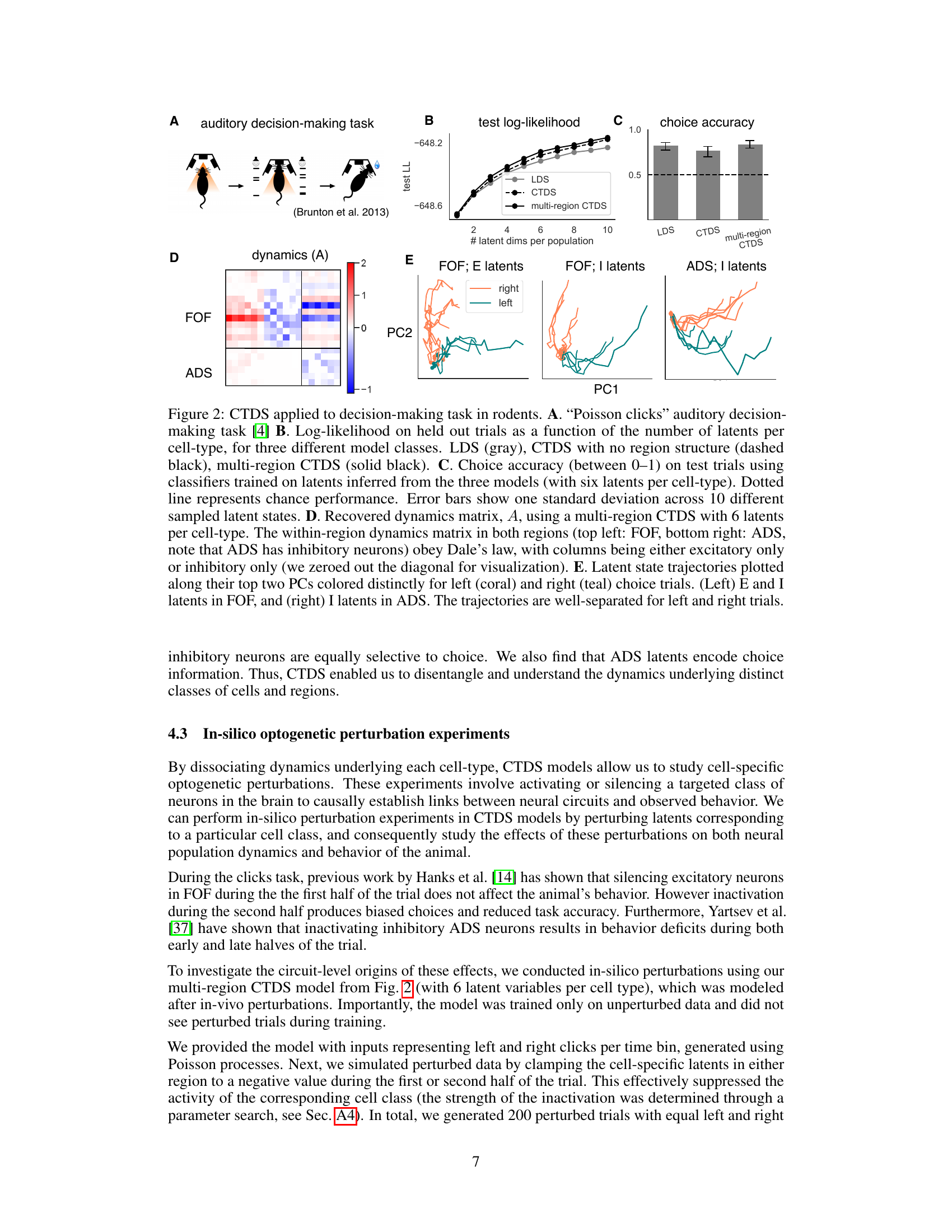
This figure demonstrates the application of the Cell-Type Dynamical Systems (CTDS) model to neural data from a rodent auditory decision-making task. Panel A illustrates the experimental task design. Panel B displays test log-likelihood for different model types (LDS, CTDS, multi-region CTDS) as a function of the number of latent dimensions. Panel C shows choice accuracy using classifiers trained on inferred latent states. Panel D shows the recovered dynamics matrix A from the multi-region CTDS model, highlighting within-region and between-region interactions. Panel E visualizes the trajectories of inferred latent states for different cell types (excitatory and inhibitory) in the FOF and ADS brain regions, demonstrating that both cell types encode information relevant to the animal’s choice.
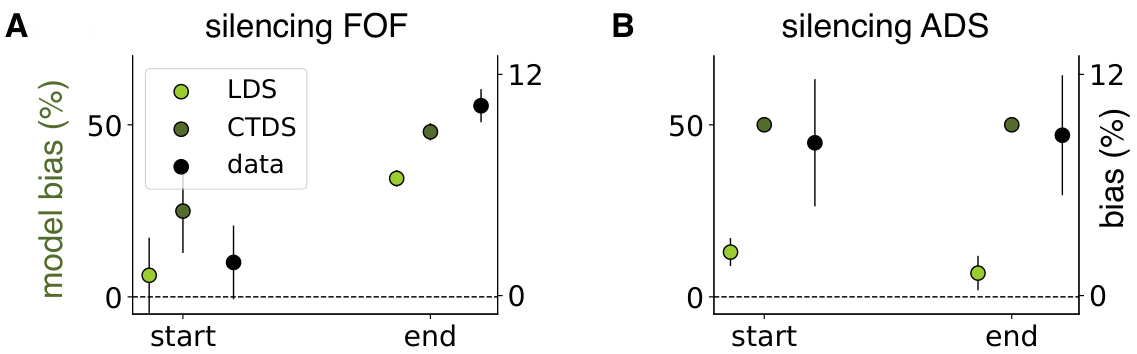
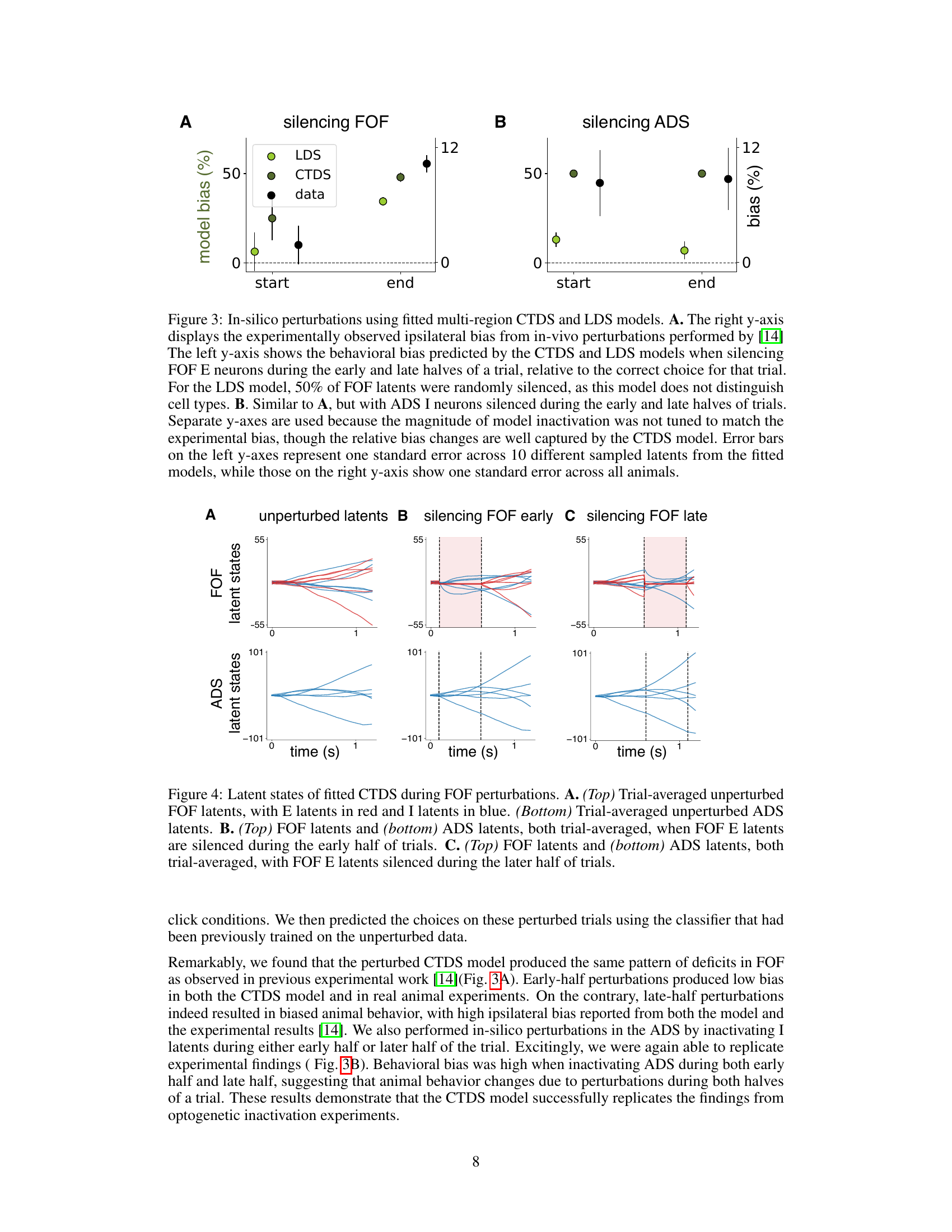
This figure displays the results of in-silico optogenetic perturbation experiments using both CTDS and LDS models. It compares the model-predicted behavioral biases with experimentally observed biases when silencing excitatory neurons in the frontal orienting fields (FOF) and inhibitory neurons in the anterior dorsal striatum (ADS) during early and late stages of a decision-making task. The CTDS model, which incorporates distinct cell types, more accurately replicates the experimental findings than the standard LDS model.
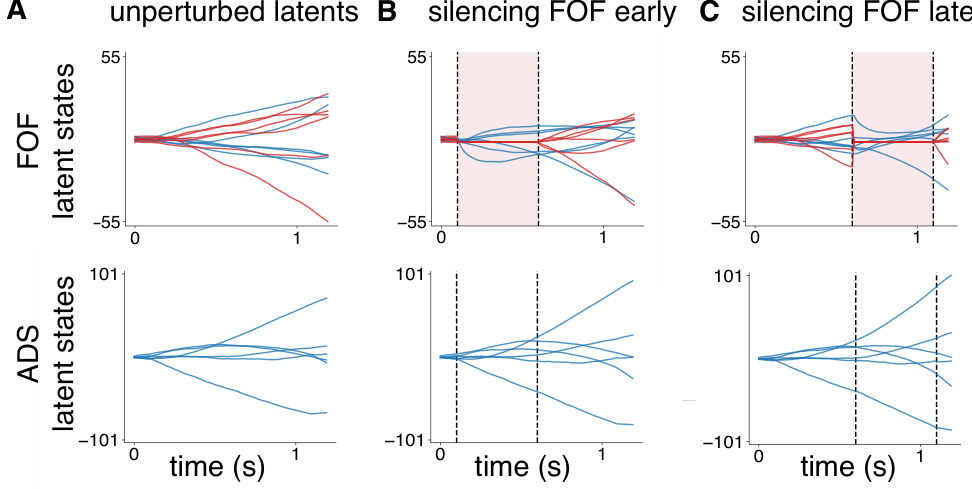
Figure 2 shows the results of applying the Cell-Type Dynamical System (CTDS) model to neural data from a rodent decision-making task. Panel A describes the experimental setup of the auditory decision-making task. Panels B and C show the performance of the CTDS model compared to other models in terms of log-likelihood and choice prediction accuracy. Panel D displays the recovered dynamics matrix, illustrating the interactions between different brain regions and cell types. Finally, Panel E presents the trajectories of latent states for different cell types, color-coded by the animal’s choice.
This figure shows the results of applying the Cell-Type Dynamical Systems (CTDS) model to neural data from a rodent decision-making task. Panel A illustrates the experimental setup of the task. Panel B shows the test log-likelihood of different models (LDS, CTDS, multi-region CTDS) as a function of the number of latent dimensions. Panel C displays the choice accuracy of classifiers trained on the inferred latent states of the different models. Panel D presents the recovered dynamics matrix from a multi-region CTDS model. Finally, Panel E visualizes the latent state trajectories of the FOF and ADS regions, colored by the animal’s choice.
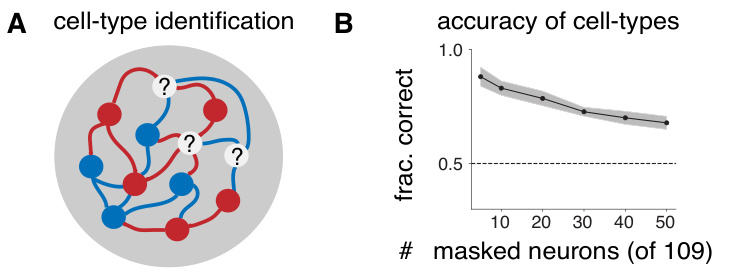
This figure demonstrates the accuracy of a novel method for inferring cell types from neural activity using the Cell-Type Dynamical System (CTDS) model. Panel A shows a schematic illustrating the problem of identifying cell types for neurons whose type is unknown. Panel B presents the results of an experiment where a CTDS model was trained on data from a subset of neurons with known cell types, and then used to predict the cell types of other neurons whose types were masked. The accuracy of the cell type predictions is shown as a function of the number of masked neurons. The error bars show the standard error over 10 random initializations. The dotted line represents the chance level of accuracy.
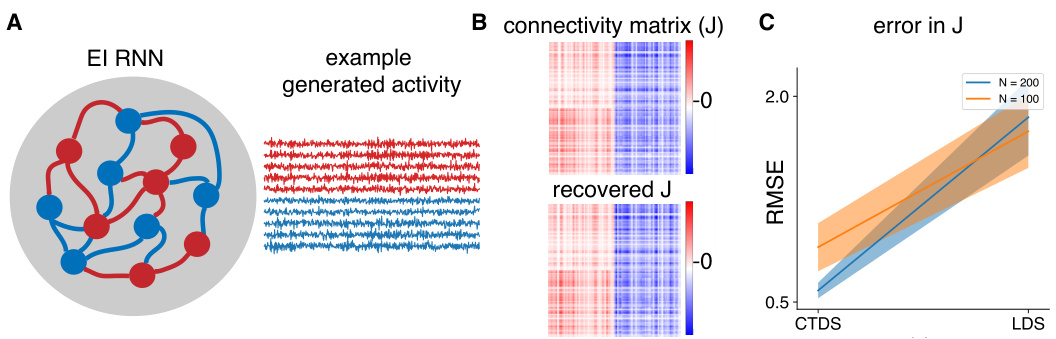
This figure shows the results of simulations performed to compare the performance of the CTDS model against a standard LDS model in recovering the connectivity matrix (J) of an E-I RNN (Excitatory-Inhibitory Recurrent Neural Network). Panel A illustrates the structure of the E-I RNN used for the simulation. Panel B compares the true connectivity matrix J with the J recovered by CTDS. Panel C shows the root mean squared error (RMSE) of J recovered by CTDS and LDS for networks with 100 and 200 units. The results demonstrate that CTDS recovers the true connectivity more accurately than LDS.

Figure 2 presents the results of applying the Cell-Type Dynamical Systems (CTDS) model to decision-making data from rodents. Panel A illustrates the experimental task design, Panel B shows the test log-likelihood as a function of the number of latents per cell type for three different models, Panel C displays choice accuracy results, and Panel D shows the recovered dynamics matrix A from a multi-region CTDS analysis. Panel E visualizes latent state trajectories for excitatory and inhibitory neurons in the frontal orienting fields (FOF) and inhibitory neurons in the anterior dorsal striatum (ADS), color-coded by the animal’s choice.
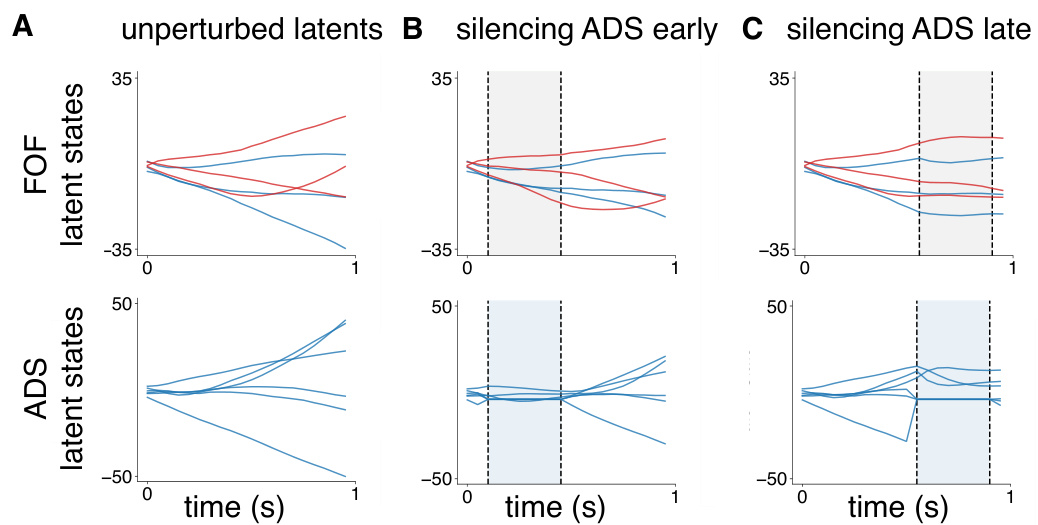
Figure 2 presents the results of applying the CTDS model to neural data from a rodent decision-making task. It shows the test log-likelihood for different models (LDS, CTDS, multi-region CTDS), choice accuracy of classifiers trained on the inferred latents, and recovered dynamics matrices. The latent state trajectories are also visualized, showing clear separation for left and right choices, indicating that both excitatory and inhibitory neurons in the FOF encode choice information and that the ADS latents encode choice information.
Full paper#