Hardness of Learning Neural Networks under the Manifold Hypothesis

↗ OpenReview ↗ NeurIPS Proc. ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial because it bridges the gap between empirical observations and theoretical understanding of neural network learnability in the context of the manifold hypothesis. It provides valuable insights into the conditions under which geometric data structure aids or hinders the learning process, guiding future research in algorithm design and complexity analysis. Furthermore, the empirical study of real-world data manifold geometry sheds light on the limitations of current assumptions, opening new avenues for more realistic theoretical modeling.

Visual Insights

#

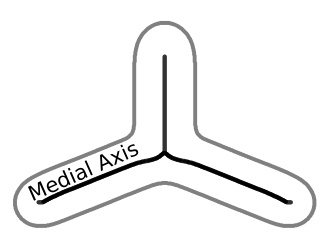
This figure illustrates the concept of ‘reach’ in a manifold. A one-dimensional manifold (a curve) is shown, along with its medial axis (the set of points that have more than one closest point on the manifold). The reach is defined as the shortest distance between the manifold and its medial axis. It provides a measure of the manifold’s overall smoothness and is important for determining whether a manifold is easily sampleable (thus learnable in the context of this paper). A small reach indicates that the manifold is relatively smooth, while a large reach indicates that the manifold has sharper curves or more complex structure.

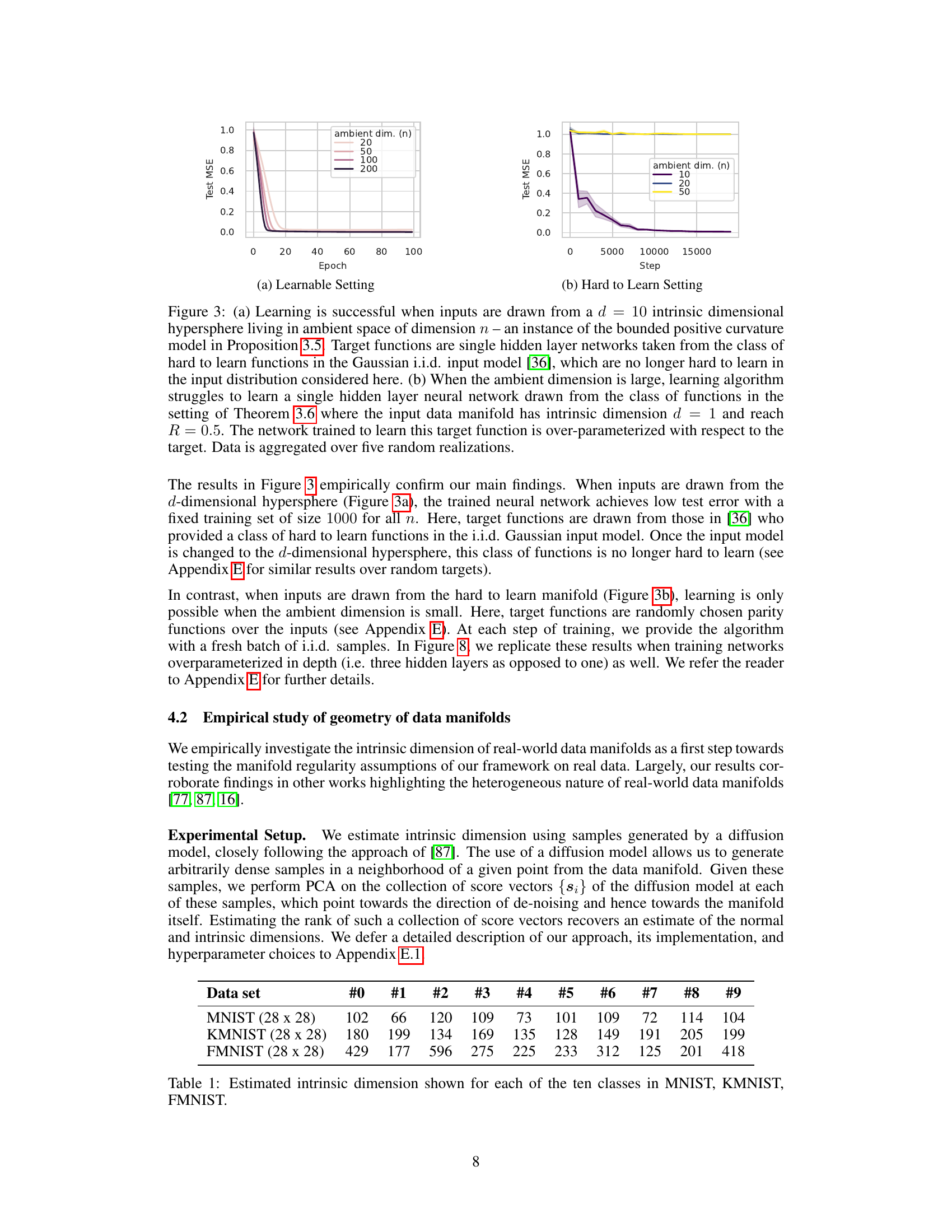
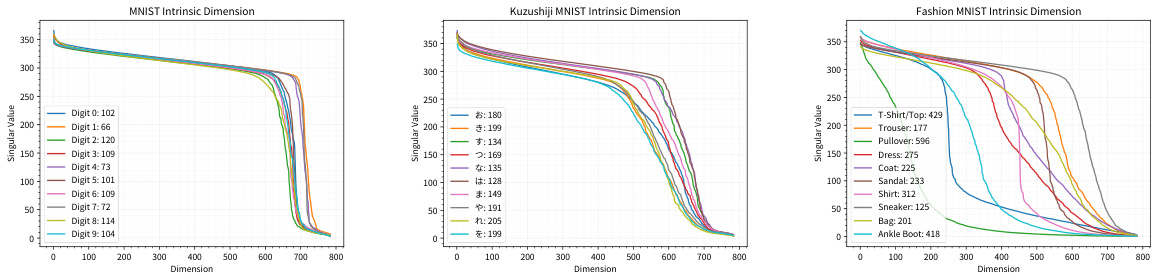
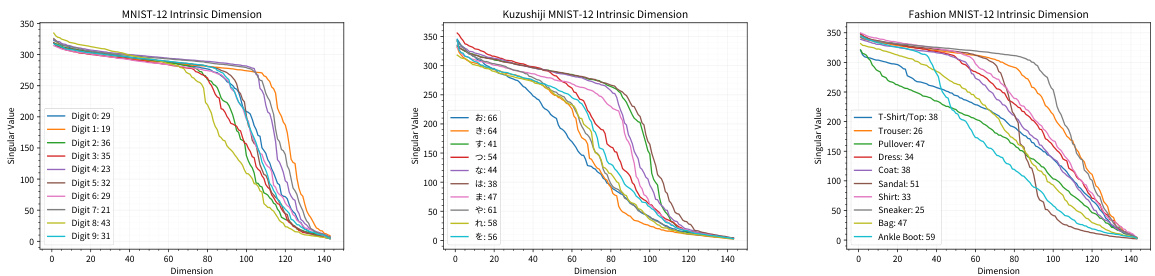
This table presents the estimated intrinsic dimension for each class in three image datasets: MNIST, KMNIST, and FMNIST. The intrinsic dimension is estimated separately for each digit class (0-9) within each dataset. The table shows that the estimated intrinsic dimension varies significantly across classes within the same dataset, suggesting a heterogeneous nature of the data manifolds. The table also shows the effect of data resolution on the intrinsic dimension, with higher resolution images having higher estimated intrinsic dimensions. This information is crucial to the paper’s analysis, helping to assess the heterogeneity of real-world data manifolds and the feasibility of making assumptions based on global geometric properties.

In-depth insights

#

Manifold Hardness

#

The concept of “Manifold Hardness” in machine learning explores the challenges of efficiently learning when high-dimensional data lies on or near a low-dimensional manifold. The core difficulty arises from the complex geometry of manifolds, which can hinder the effectiveness of standard learning algorithms. This complexity is not simply about the data’s dimensionality; rather, it’s about its intrinsic structure, including curvature and other geometric properties that may be difficult to capture with simple models. The paper likely investigates minimal assumptions on manifold properties (curvature, volume, etc.) needed to ensure efficient learnability. It may demonstrate hardness results under certain geometric constraints showing that without additional assumptions, learning becomes computationally infeasible. Conversely, the paper likely shows that relaxed geometric conditions (such as manifolds reliably reconstructable via manifold learning) lead to efficient learnability. This highlights a crucial trade-off between the complexity of the manifold and the feasibility of learning from it. This is a significant contribution because it provides a deeper understanding of the computational aspects of machine learning under realistic data assumptions.

Learnable Manifolds

#

The concept of “learnable manifolds” in the context of neural network training centers on the idea that data manifolds with specific geometric properties are more easily learned by neural networks than others. The paper investigates the conditions under which this holds. The key is to link the geometric properties of the data manifold (such as its curvature, volume, and smoothness) to the computational complexity of learning. Efficiently sampleable manifolds, those that can be well-approximated by a relatively small number of samples, are shown to be efficiently learnable. This is because a simple interpolation argument suffices to accurately reconstruct the target function. Conversely, manifolds with bounded curvature but unbounded volume are shown to be provably hard to learn. The key difficulty stems from the fact that these manifolds can cover exponentially many quadrants of the hypercube, thus reducing the learnability problem to learning a hard Boolean function. Real-world data, however, is expected to have heterogeneous characteristics and not necessarily conform to the simple geometric structures analyzed, thus requiring further investigation into the intermediate cases between these two extremes.

Reach & Volume

#

The concepts of “Reach” and “Volume” in manifold learning are crucial for understanding the learnability of neural networks on data manifolds. Reach, a measure of local curvature, quantifies how far a point can be from the manifold while still having a unique nearest neighbor. A large reach indicates a smooth, flat manifold, making it easier to sample and learn from. In contrast, a small reach indicates high curvature, posing significant challenges for learning algorithms. Volume, the measure of the manifold’s size, impacts sample complexity. A high-volume manifold needs many more samples for accurate representation, making learning more computationally expensive. The interplay between reach and volume determines the complexity of learning. Manifolds with large reach and small volume are easily learnable, while those with small reach or large volume pose significant challenges. The paper explores these relationships, showing that additional assumptions on manifold volume can alleviate hardness results found under bounded curvature. The authors demonstrate these trade-offs through theoretical analysis and experiments, highlighting the importance of considering both reach and volume when evaluating the learnability of neural networks.

Geometry of Data

#

The geometry of data is a crucial concept in modern machine learning, impacting model design and performance. High-dimensional data often resides on or near a low-dimensional manifold, a concept underpinning the manifold hypothesis. This hypothesis suggests that complex, high-dimensional data might possess an underlying simpler structure, which allows for more efficient learning and analysis. Understanding this geometry involves exploring concepts like intrinsic dimensionality, curvature, and reach, which quantify the data’s inherent structure and smoothness. These geometric properties significantly influence the learnability of neural networks. For example, manifolds with bounded curvature and volume are shown to be efficiently learnable, while those with unbounded volume, even under bounded curvature, may present challenges for learning algorithms. The study of data geometry thus moves beyond the simplistic view of data points in Euclidean space, revealing fundamental insights into the complexity of machine learning problems and suggesting directions for the design of more effective algorithms.

Future Research

#

Future research directions stemming from this work are multifaceted. Extending the learnability analysis to incorporate more realistic data manifold characteristics is crucial. Real-world data often exhibits heterogeneity, deviating from the idealized, globally smooth manifolds assumed in many theoretical analyses. Investigating intermediate regimes where manifolds possess heterogeneous features (e.g., varying intrinsic dimension, non-uniform curvature) is vital. Developing novel learning algorithms specifically tailored to these complex data geometries presents a significant challenge. The findings suggest exploring alternative algorithmic approaches, possibly drawing upon the strengths of manifold learning techniques for data preprocessing or model regularization. Connecting the theoretical findings to practical neural network architectures is another important direction. The study primarily focuses on feedforward networks; applying the insights obtained to convolutional and recurrent architectures requires further exploration. Finally, exploring the interplay between data geometry and specific neural network properties (e.g., depth, width, activation functions) to further refine the understanding of learnability remains an open and promising research area.

More visual insights

#

More on figures

This figure summarizes the main findings of the paper regarding the learnability of neural networks trained on data drawn from different types of manifolds. It highlights three regimes: efficiently sampleable manifolds (learnable), heterogeneous manifolds (potentially learnable), and manifolds with bounded curvature but unbounded volume (provably hard). The figure visually represents these regimes with different manifold shapes and provides examples of each.

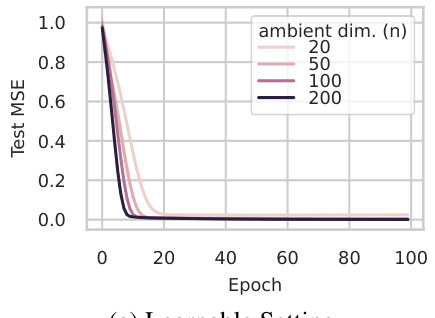
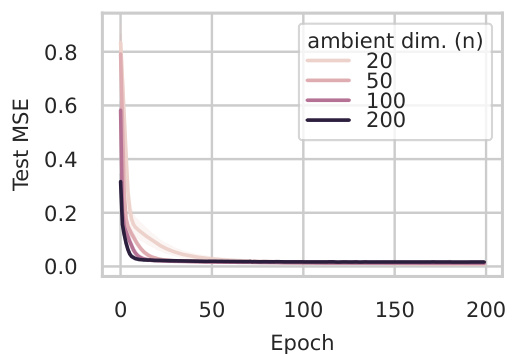
This figure shows the results of training neural networks on two different types of data manifolds: (a) shows a learnable manifold (efficiently sampleable), while (b) shows a provably hard manifold. The results confirm the theoretical findings of the paper; neural networks learn efficiently on the learnable manifold, but struggle on the hard manifold when the ambient dimension is large.

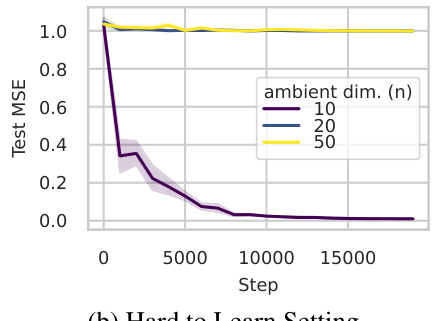
This figure shows the results of learning experiments on two types of manifolds: efficiently sampleable manifolds (learnable) and manifolds with bounded curvature but unbounded volume (hard to learn). The left subplot shows that learning is successful on efficiently sampleable manifolds, even when the target functions are those proven hard to learn under the i.i.d. Gaussian input model. The right subplot shows that learning is significantly more difficult on manifolds with bounded curvature but unbounded volume as the ambient dimension increases, highlighting the hardness result.

This figure summarizes the main findings of the paper regarding the learnability of neural networks trained on data lying on manifolds. The x-axis represents different regimes of manifolds categorized by their properties (efficiently sampleable, heterogeneous, provably hard). The y-axis implicitly represents the learnability of neural networks in each regime. Efficiently sampleable manifolds are those that can be well-approximated by a relatively small number of samples, rendering neural network training efficient. Heterogeneous manifolds represent real-world scenarios where manifold properties may vary across the data. Provably hard manifolds are those where learning is proven to be computationally difficult, even with relatively simple network architectures. The figure highlights that real-world data likely falls in the heterogeneous regime, where learnability remains an open question.

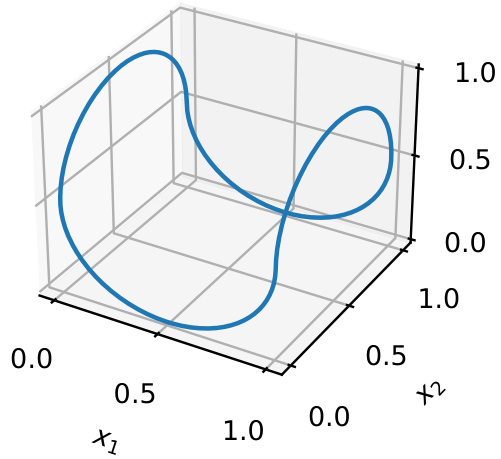
This figure shows a 3D plot of a one-dimensional manifold M3 constructed using the method described in the paper. The manifold resembles a space-filling curve that wraps around the unit cube, visiting many of its corners. It demonstrates a low-dimensional manifold embedded in a higher-dimensional space (3D in this case). The shape illustrates the construction technique used in the paper to create manifolds with bounded curvature but unbounded volume. This is relevant to their study of the hardness of learning under manifold assumptions. The curve touches many quadrants of the unit hypercube, which is important in proving their hardness results.

This figure shows the results of experiments on learning neural networks with inputs sampled from two different types of manifolds. (a) demonstrates successful learning when inputs are from a hypersphere with bounded positive curvature. (b) shows difficulty in learning when the inputs are from a manifold with bounded curvature and unbounded volume, especially as the ambient dimension increases. The results confirm the theoretical findings about the relationship between manifold properties and learnability.

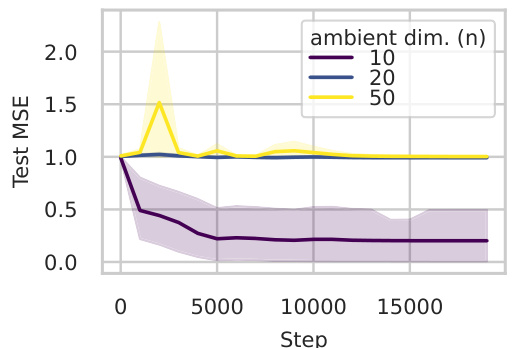
This figure shows the results of the experiments conducted to verify the main findings of the paper. (a) shows that neural networks are learnable when inputs come from an efficiently sampleable manifold (d=10 hypersphere in higher dimensional space). (b) demonstrates that learning is hard when the input manifold has bounded curvature but unbounded volume (reach R=0.5, d=1). The results confirm the theory developed in the paper.

This figure summarizes the main findings of the paper regarding the learnability of neural networks trained on data sampled from different types of manifolds. It highlights three regimes: an efficiently sampleable regime where learnability is guaranteed, a provably hard regime where learning is difficult, and an intermediate heterogeneous regime representing real-world data, where learnability remains an open question. The figure visually represents these regimes and illustrates how the geometric properties of the manifold (smoothness, curvature, volume) impact the learnability of the neural network.

This figure illustrates the relationship between the learnability of neural networks and the geometric properties of the input data manifold. It shows that efficient learnability is possible for manifolds that can be well-approximated by samples (efficiently sampleable), using a simple interpolation argument. Conversely, for manifolds characterized only by curvature and intrinsic dimension bounds, there exist classes that make learning computationally hard. Real-world data manifolds likely exhibit heterogeneous features, falling within an intermediate regime between these two extremes.

More on tables

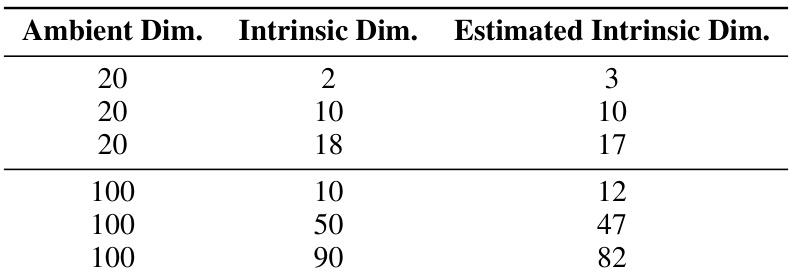
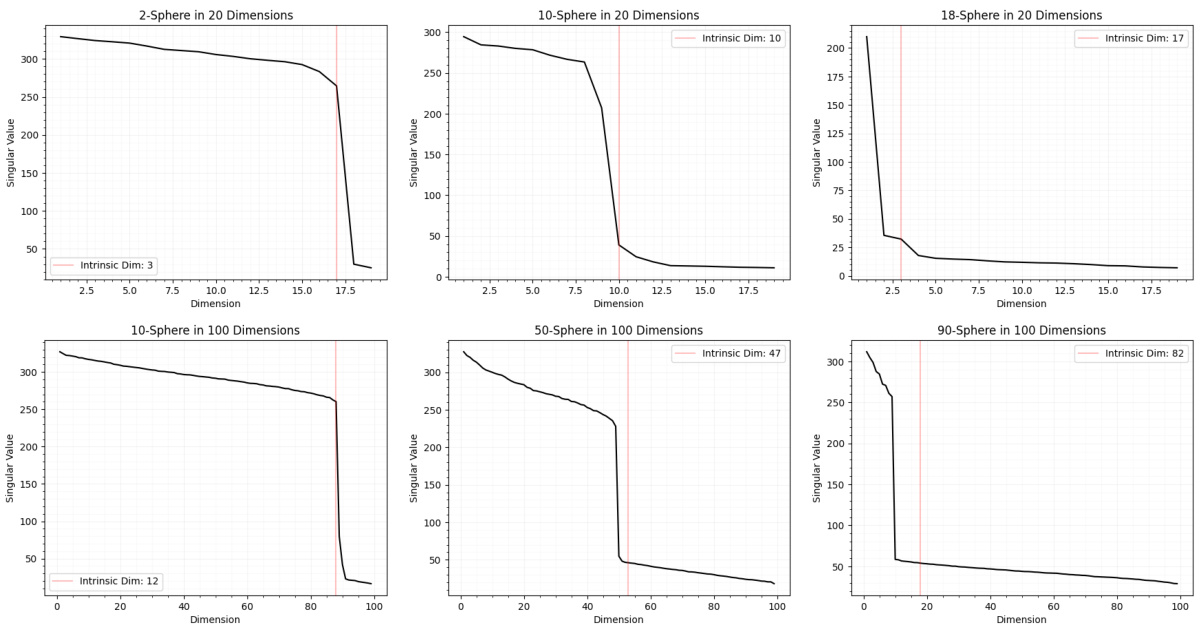
This table presents the results of estimating the intrinsic dimension of hyperspheres embedded in higher dimensional ambient spaces. The true intrinsic dimension and the estimated intrinsic dimension are compared for various combinations of ambient and intrinsic dimensions. The purpose is to validate the accuracy of the method used to estimate intrinsic dimension.

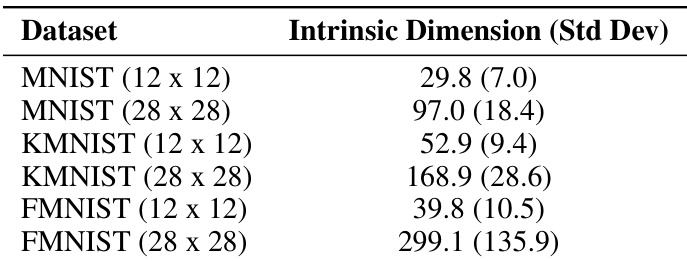
This table presents the estimated intrinsic dimension for three image datasets: MNIST, KMNIST, and FMNIST. The intrinsic dimension is estimated separately for each of the ten classes within each dataset. Two different image resolutions are considered for each dataset: 12x12 and 28x28 pixels. The table shows the mean and standard deviation of the estimated intrinsic dimension for each class and resolution. These results highlight the heterogeneity of the intrinsic dimension across different classes in each dataset.

Full paper

#