Semi-Supervised Sparse Gaussian Classification: Provable Benefits of Unlabeled Data

↗ OpenReview ↗ NeurIPS Proc. ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial because it provides theoretical guarantees for the benefits of semi-supervised learning (SSL) in high-dimensional settings, a significant advancement in the field. It also introduces a novel polynomial-time algorithm, LSPCA, showing the practical potential of SSL and prompting further research into computationally efficient SSL methods and their applications.

Visual Insights

#

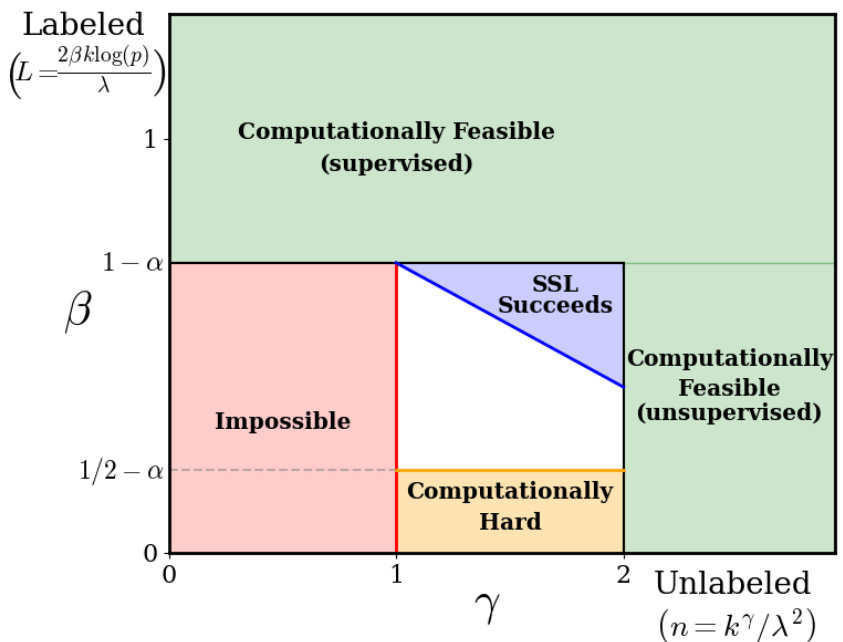
This figure shows different regions in the (γ, β) plane, where γ represents the number of unlabeled samples and β represents the number of labeled samples. The red region shows where classification and feature selection are impossible. The green region shows where support estimation is computationally feasible using only unlabeled data. The orange region shows where accurate classification and feature selection are computationally hard. The blue region shows where it is possible to construct an accurate SSL classifier in polynomial time. The white region is where the feasibility of classification and feature selection are unknown. The x-axis represents the amount of unlabeled data and the y-axis represents the amount of labeled data.

In-depth insights

#

Sparse Gaussian SSL

#

Sparse Gaussian semi-supervised learning (SSL) tackles the challenge of classifying high-dimensional data with limited labeled examples, leveraging the abundance of unlabeled data. Sparsity, meaning only a few features are truly relevant, is a crucial assumption. The Gaussian assumption simplifies modeling data distribution. Research in this area often explores theoretical bounds on classification accuracy and feature selection, determining the minimum amount of labeled and unlabeled data required for successful classification. Information-theoretic limits and computational complexity under conjectures like the low-degree likelihood ratio hardness are investigated to understand the fundamental limits of SSL algorithms. Algorithms, like sparse PCA variants, are developed and analyzed to efficiently exploit the structure inherent in sparse Gaussian data to improve accuracy beyond what’s achievable with supervised or unsupervised learning alone. The theoretical analysis aims to identify regimes where SSL provably outperforms these methods, highlighting the benefits of unlabeled data in high dimensions.

Provable SSL Gains

#

The heading ‘Provable SSL Gains’ suggests a focus on demonstrating the advantages of semi-supervised learning (SSL) rigorously. This likely involves presenting theoretical results or bounds that show when and how SSL surpasses supervised learning (SL) or unsupervised learning (UL) in a quantifiable way. The research likely establishes conditions under which the incorporation of unlabeled data demonstrably improves model performance, moving beyond mere empirical observations. Information-theoretic analysis or computational complexity arguments could be employed to rigorously support these claims. The analysis might explore different data regimes to reveal where SSL provably offers advantages, specifying critical relationships between the amount of labeled data, the amount of unlabeled data, and the problem’s dimensionality. A key outcome might be identifying situations where SSL is not only empirically better but also theoretically guaranteed to be superior, highlighting its strengths in specific contexts. Ultimately, the goal is to provide a strong theoretical foundation for understanding and leveraging the benefits of SSL, offering clear guidelines for when to expect provable gains.

LSPCA Algorithm

#

The LSPCA (Label Screening PCA) algorithm, a semi-supervised learning scheme, tackles high-dimensional sparse Gaussian classification by cleverly combining labeled and unlabeled data. Its core innovation lies in a two-stage process: first, label screening efficiently filters out irrelevant features using labeled data, significantly reducing dimensionality. Second, PCA is applied to the remaining features using unlabeled data to accurately estimate the support of the sparse difference in class means. This approach is particularly effective in regimes where traditional supervised or unsupervised methods fail, demonstrating the power of combining labeled and unlabeled data. The algorithm’s polynomial runtime complexity makes it computationally feasible even in high dimensions, showcasing its practical applicability. Importantly, theoretical analysis proves its advantage over purely supervised or unsupervised techniques under specific conditions, thereby establishing provable benefits of semi-supervised learning in this setting.

Computational Bounds

#

The section on “Computational Bounds” likely explores the inherent computational limitations of solving the sparse Gaussian classification problem. The authors probably investigate the time complexity of algorithms used, potentially demonstrating a trade-off between accuracy and computational feasibility. Information-theoretic lower bounds might be presented, showing the minimum amount of data required for successful feature selection and classification, regardless of the algorithm. Furthermore, the analysis likely delves into computational hardness by employing techniques like the low-degree likelihood ratio conjecture, establishing that finding the optimal solution is computationally intractable under certain conditions. This might involve showing the existence of a statistical-computational gap, where information-theoretically feasible solutions are practically infeasible to compute efficiently. Ultimately, this section aims to rigorously characterize the problem’s difficulty, providing insights into the algorithmic limits of achieving accurate classifications with limited computational resources. The presented computational bounds offer a valuable benchmark for algorithm design in this area, highlighting the need for efficient and effective heuristics in the face of inherent computational barriers.

Future of SSL

#

The future of semi-supervised learning (SSL) is bright, driven by several key factors. Improved theoretical understanding will lead to more robust and efficient algorithms, moving beyond heuristic approaches towards principled methods with provable guarantees. Advances in representation learning will allow SSL to leverage unlabeled data more effectively, particularly in high-dimensional settings where traditional methods struggle. Increased focus on addressing biases and ethical concerns within SSL will be crucial, ensuring fair and equitable outcomes. The development of new SSL methods for specific application domains, such as natural language processing and computer vision, will lead to specialized solutions that exploit domain-specific structures. Greater emphasis on combining SSL with other machine learning paradigms, such as reinforcement learning and transfer learning, promises to unlock even greater potential. Finally, the expanding availability of large, diverse unlabeled datasets will provide essential fuel for future SSL advancements, fostering innovation and pushing the boundaries of what’s possible.

More visual insights

#

More on figures

This figure shows the results of empirical simulations comparing several semi-supervised learning (SSL), supervised learning (SL), and unsupervised learning (UL) algorithms on a sparse high-dimensional Gaussian classification task. The left panel displays the support recovery accuracy, showing the fraction of correctly identified features for each method as the number of unlabeled samples (n) increases. The right panel displays the classification error rate of the different methods, where lower error rates indicate better performance. The results highlight the benefits of combining labeled and unlabeled data for accurate classification in high-dimensional sparse settings. LSPCA and LS2PCA, the proposed SSL methods, consistently show superior performance to SL and UL techniques.

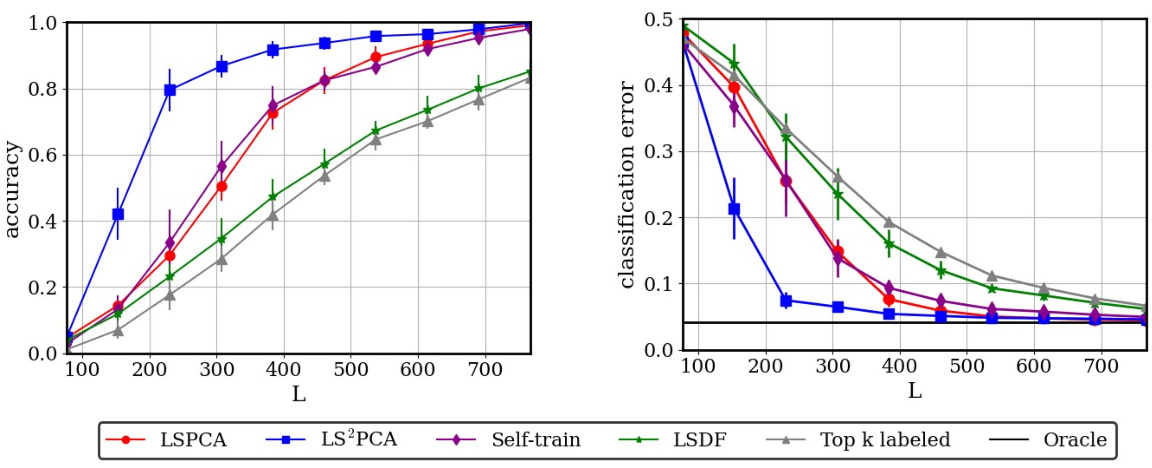
The figure shows empirical results comparing the performance of several semi-supervised learning algorithms for sparse Gaussian classification in high dimensions. The left panel displays the support recovery accuracy (the fraction of correctly identified features) of different algorithms as the number of labeled samples (L) increases, while keeping the number of unlabeled samples fixed. The right panel shows the corresponding classification error rates. The algorithms compared include LSPCA (proposed), LS2PCA (an improved variant of LSPCA), a self-training algorithm, LSDF, and a top-k labeled data-only method. The results demonstrate the superiority of the proposed LSPCA and LS2PCA algorithms over supervised, unsupervised and other SSL approaches, highlighting the provable benefits of combining labeled and unlabeled data in this setting.

Full paper

#