↗ OpenReview ↗ NeurIPS Proc. ↗ Chat
TL;DR#
Learning halfspaces with margins under noise is a fundamental problem in machine learning. Existing algorithms for Massart noise, a more realistic noise model, had suboptimal sample complexities compared to those under the simpler random classification noise. This was believed to reflect the inherent difficulty in managing the non-uniformity of Massart noise.
This paper introduces Perspectron, a novel algorithm that addresses this issue. By cleverly re-weighting samples and using a perceptron-like update, it achieves the optimal sample complexity, matching the best results for random classification noise. This improvement extends to generalized linear models, offering a significant advancement in the field.
Key Takeaways#
Why does it matter?#
This paper is crucial because it significantly advances our understanding of learning under Massart noise, a more realistic noise model than previously studied ones. Its findings improve the efficiency of existing algorithms and open new avenues for developing robust learning methods applicable to a wider range of real-world problems. The improved sample complexity guarantees are particularly valuable for high-dimensional data scenarios.
Visual Insights#
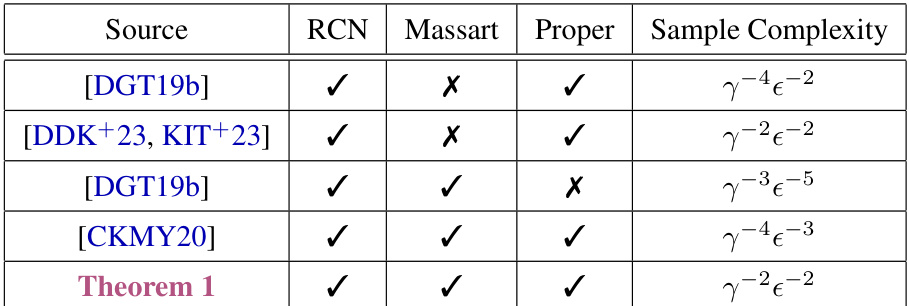
The table compares the sample complexities of various algorithms for learning halfspaces with a margin under different noise models. It shows the sample complexity as a function of the margin (γ) and error (ε). The columns indicate whether the algorithm handles Random Classification Noise (RCN), Massart noise, and produces a proper or improper hypothesis. The table highlights that the proposed Perspectron algorithm achieves a sample complexity comparable to state-of-the-art RCN learners, even under the more challenging Massart noise.
Full paper#



















