↗ OpenReview ↗ NeurIPS Proc. ↗ Chat
TL;DR#
Diffusion models are powerful generative models but their inference cost is high, especially for high-dimensional data. Existing methods struggle with polynomial time complexity for high-dimensional data which limits their application. This is due to sequential sampling iterations and the computational cost of evaluating the score function. This paper addresses the limitation by reducing the inference time complexity.
The proposed algorithms, PIADM-SDE/ODE, divide sampling into independent blocks, enabling parallel processing of Picard iterations. This clever approach leads to a significant improvement in time complexity to poly-logarithmic (Õ(poly log d)), the first of its kind with provable sub-linear complexity. The method is compatible with both stochastic differential equation (SDE) and probability flow ordinary differential equation (ODE) implementations, with PIADM-ODE improving space complexity. This breakthrough opens up applications for high-dimensional data analysis.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working with diffusion models, especially those dealing with high-dimensional data where inference speed is a major bottleneck. It provides the first implementation with provable sub-linear time complexity, significantly advancing the field and opening up possibilities for applying diffusion models to even larger datasets. It also presents new parallelization strategies and rigorous theoretical analysis, making it a valuable resource for both theoretical and applied researchers.
Visual Insights#
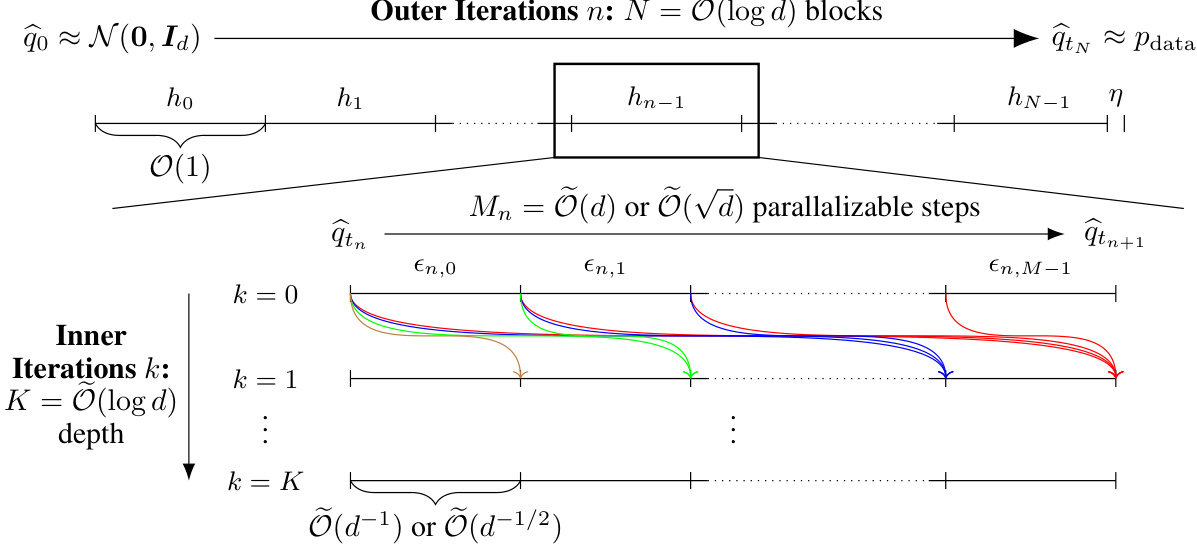
This figure illustrates the PIADM-SDE/ODE algorithm. The sampling process is divided into outer iterations (blocks) and inner iterations. The outer iterations, O(log d) in number and O(1) in length, represent the main progress towards the data distribution. Within each outer iteration, parallel inner iterations (Õ(d) for SDE, Õ(√d) for ODE) refine the sample. The overall time complexity is polylogarithmic in the data dimension (d), a significant improvement over previous methods. The colored curves depict the computational steps within a single outer iteration.
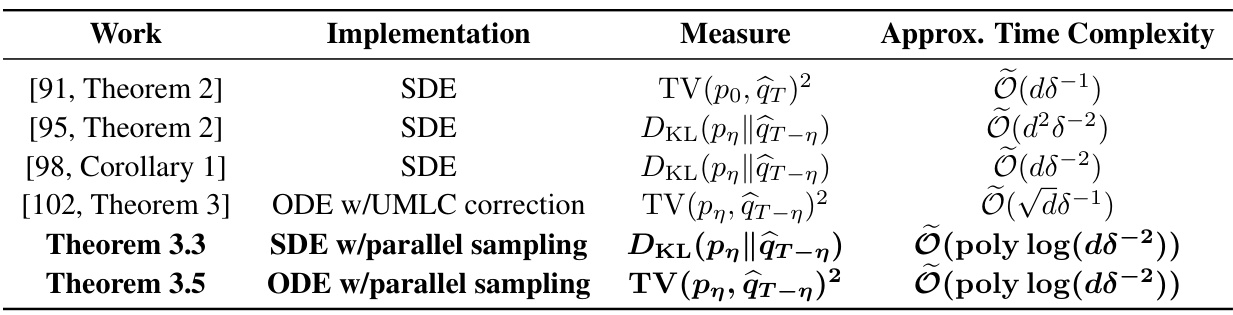
This table compares the approximate time complexity of different implementations of diffusion models from existing research papers. The approximate time complexity is defined as the number of unparallelizable evaluations of the learned neural network-based score function. It shows how the time complexity scales with the data dimension (d) and a smoothing parameter (η). The table includes results for SDE and ODE implementations, both with and without parallel sampling techniques. The results highlight the improvement in computational efficiency achieved by parallel sampling in reducing the time complexity.
Full paper#