Analysing Multi-Task Regression via Random Matrix Theory with Application to Time Series Forecasting

↗ OpenReview ↗ NeurIPS Proc. ↗ Hugging Face ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial for researchers in machine learning and time series analysis. It offers novel theoretical insights into multi-task regression, provides a practical hyperparameter optimization method, and demonstrates significant improvements in multivariate time series forecasting. The research opens new avenues for applying random matrix theory to complex models and addressing the challenges of high-dimensional data.

Visual Insights

#

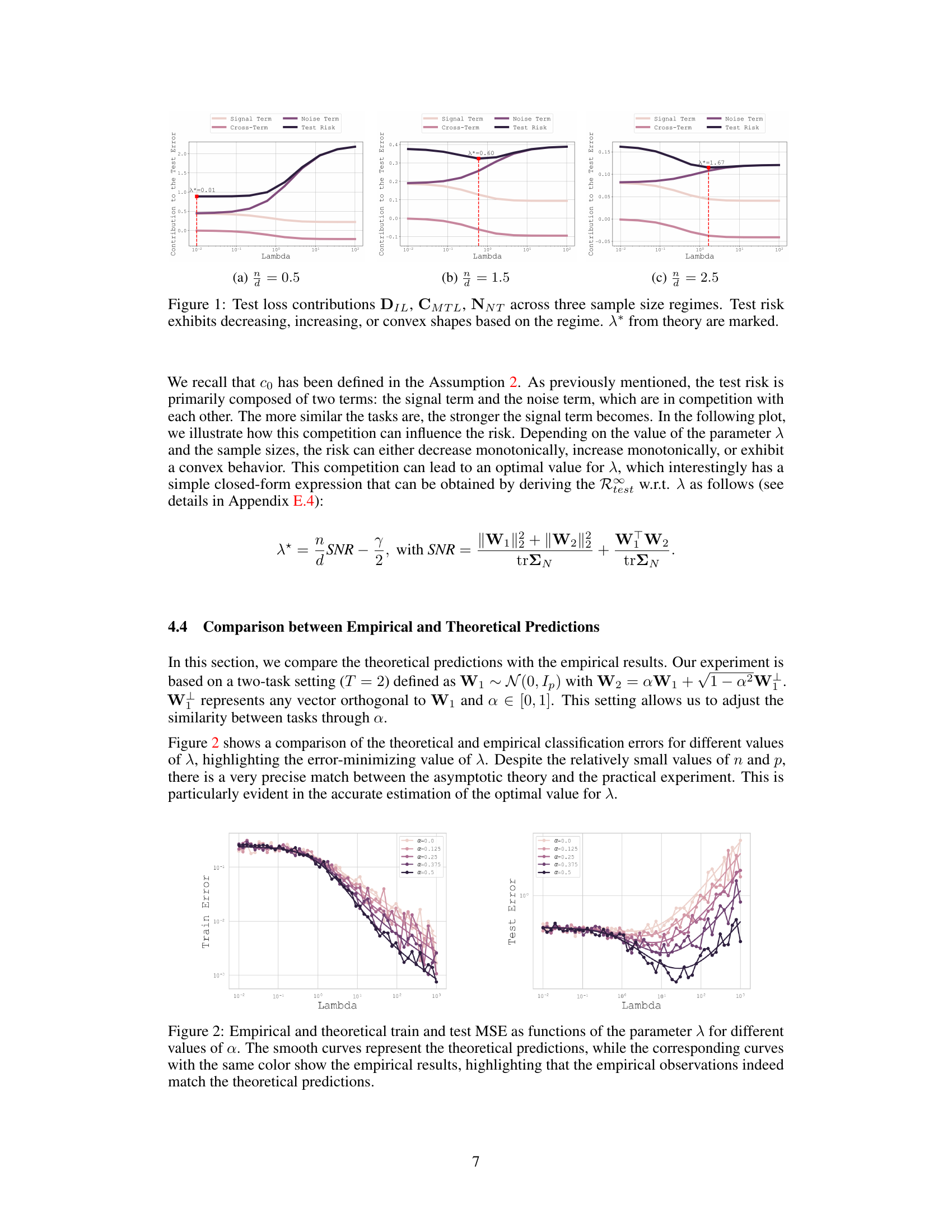
This figure shows the breakdown of the test loss into three components: the independent learning term (DIL), the cross-term (CMTL) representing multi-task learning, and the noise term (NNT) representing negative transfer. The plots illustrate how these components interact for three different sample size regimes (n/d = 0.5, 1.5, and 2.5). The test risk curve, shown in black, exhibits different behaviors depending on the sample size regime: monotonically decreasing, monotonically increasing, or convex. The optimal lambda values (λ*) predicted by the theory are also marked on the plots with red dashed lines, highlighting their consistency with the test risk curves.

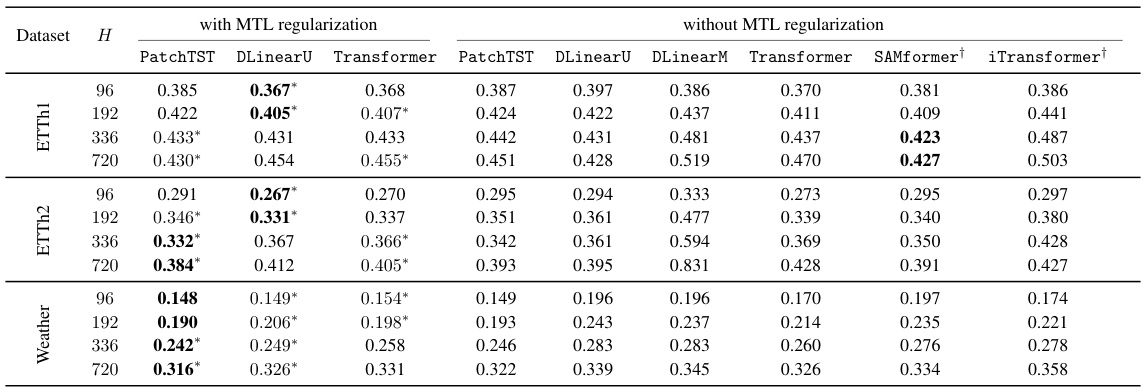
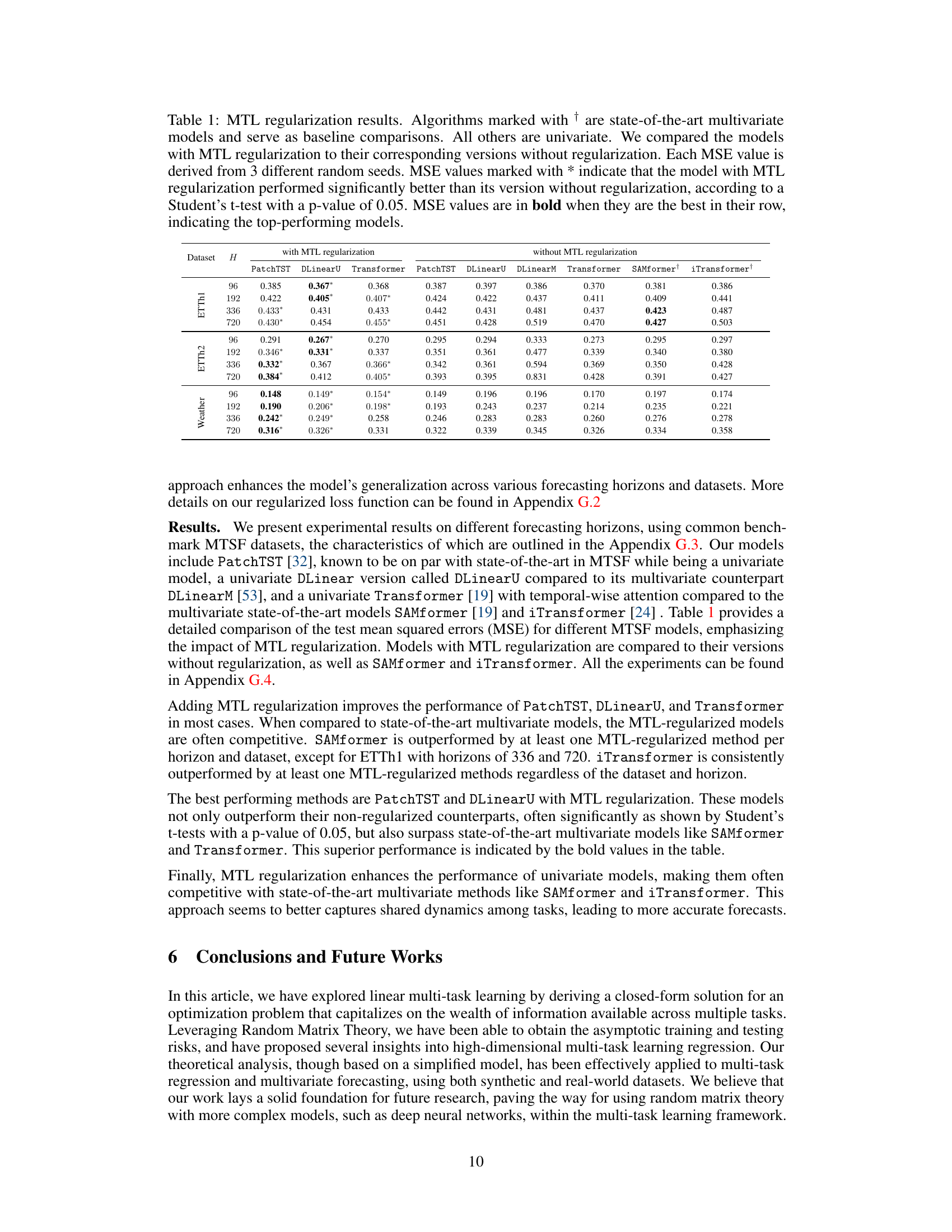
This table presents the results of applying multi-task learning (MTL) regularization to several univariate time series forecasting models. It compares the mean squared error (MSE) achieved by these models both with and without MTL regularization, and also against several state-of-the-art multivariate models. The statistical significance of the improvements from MTL regularization is indicated using a Student’s t-test.

In-depth insights

#

MTL via Random Matrix

#

The heading ‘MTL via Random Matrix’ suggests a novel approach to multi-task learning (MTL) leveraging random matrix theory. This framework likely uses random matrix theory’s tools to analyze and optimize MTL models, particularly in high-dimensional settings where traditional methods may falter. A key advantage could be deriving precise performance estimations, moving beyond typical bounds and providing more accurate insights into model behavior. The theoretical analysis probably involves deriving closed-form solutions or deterministic equivalents for MTL optimization problems. This allows for precise risk assessment, identifying optimal hyperparameters, and potentially mitigating the risk of negative transfer (where learning one task harms others). The results from this analysis likely offer practical insights into how model statistics, data covariances, and task relationships affect MTL performance. Ultimately, this approach promises improved accuracy and a robust theoretical foundation for high-dimensional multi-task regression and other applications.

High-D Multi-task Risks

#

Analyzing high-dimensional multi-task learning risks necessitates a nuanced approach. Random Matrix Theory (RMT) provides a powerful framework for deriving precise performance estimations, particularly when dealing with non-Gaussian data distributions often encountered in real-world scenarios. A key focus is disentangling the complex interplay between shared information across tasks (positive transfer) and task-specific deviations (negative transfer). Closed-form solutions are highly valuable for understanding how model parameters influence these effects. Closed-form solutions allow us to pinpoint optimal hyperparameter settings which maximize signal terms (representing positive transfer) while mitigating noise amplification and negative transfer. This rigorous analysis ultimately guides effective hyperparameter optimization, leading to improved generalization and more robust multi-task regression models. A significant advantage of the RMT-based approach is its ability to handle high-dimensional data effectively where traditional methods often fail.

MTSF Application

#

The MTSF application section likely details how the proposed multi-task regression framework enhances multivariate time series forecasting (MTSF). It probably showcases the method’s effectiveness by comparing its performance against traditional univariate models and state-of-the-art multivariate models. Key aspects would include a description of how MTSF is framed as a multi-task problem, likely by treating each time series as a separate task. The application might detail experimental results on various benchmark datasets, demonstrating improved accuracy and efficiency in forecasting multiple time series simultaneously. A crucial element would be a discussion of hyperparameter optimization, explaining how the framework’s theoretical insights aid in tuning model parameters for optimal performance. This section may also discuss the benefits of leveraging multivariate information, contrasting the results with those obtained by applying univariate methods to each time series independently. The authors likely emphasize the practical applicability and the significant improvement over traditional approaches, highlighting the advantages of their theoretical framework in real-world settings.

Hyperparameter Opt.

#

The heading ‘Hyperparameter Opt.’ suggests a crucial section dedicated to optimizing model parameters. It likely delves into methods for determining optimal values for hyperparameters, which are settings that control the learning process but are not learned directly from the data. The discussion likely covers various strategies, possibly including cross-validation, grid search, Bayesian optimization, or more sophisticated techniques. A strong section would highlight the importance of robust hyperparameter tuning for achieving optimal model performance and generalizability. It’s likely that the authors present both theoretical justification and empirical evidence supporting their chosen method, potentially comparing multiple approaches to demonstrate the effectiveness of their chosen approach. The section might also address the challenges associated with hyperparameter optimization in high-dimensional spaces, as well as considerations for computational cost and resource efficiency. Addressing the practical implementation of their proposed technique would be critical for reader understanding.

Future Work

#

The paper’s ‘Future Work’ section would ideally explore extending the theoretical framework beyond linear models to encompass complex architectures like deep neural networks. This is crucial as the current linear model, while providing valuable insights, might not fully capture the complexities of real-world datasets, especially in time series forecasting. Investigating the impact of non-Gaussian data distributions on the theoretical results would also enhance the applicability of the framework to a wider range of applications. Further research should focus on developing robust methods for hyperparameter optimization in the non-linear settings, moving beyond the oracle approach used in the current study. Finally, a comprehensive investigation into the impact of various data characteristics and their interaction with multi-task learning performance, is needed to provide a more comprehensive theoretical understanding.

More visual insights

#

More on figures

This figure compares the empirical and theoretical mean squared error (MSE) for both training and testing data across various values of the regularization parameter λ and different levels of task similarity (α). The smooth curves represent the theoretical MSE calculated using the proposed random matrix theory-based framework, while the corresponding curves with the same color show the empirical MSE obtained from experiments. The close alignment between the theoretical and empirical results confirms the accuracy of the proposed framework, particularly in estimating the optimal value of λ.

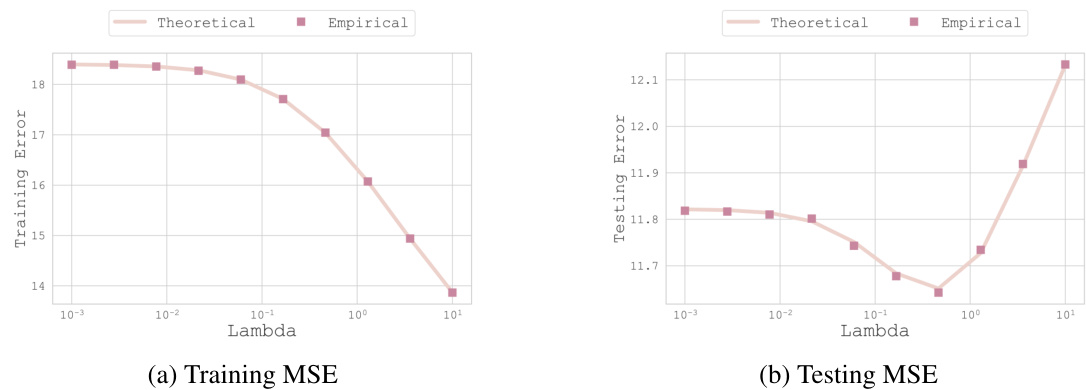
This figure compares the theoretical and empirical Mean Squared Errors (MSE) for training and testing data across a range of regularization parameter (lambda) values. The close agreement between the theoretical predictions and empirical results validates the accuracy of the theoretical model developed in the paper. The experiment uses the first two channels of a dataset as two separate tasks, with 144 features (d=144), 95 samples for training, and 42 for testing.

This figure shows the results of applying the proposed optimization method to the PatchTST baseline model on three different datasets (ETTh1, ETTh2, and Weather) and four different forecasting horizons (96, 192, 336, and 720). Each subplot represents a different dataset and horizon. The x-axis represents the lambda values, and the y-axis represents the average Mean Squared Error (MSE). Multiple lines are plotted within each subplot, each corresponding to different gamma values. The plots illustrate how the optimal lambda value changes across various datasets, horizons, and gamma values, highlighting the effectiveness of the proposed method in finding optimal hyperparameters.

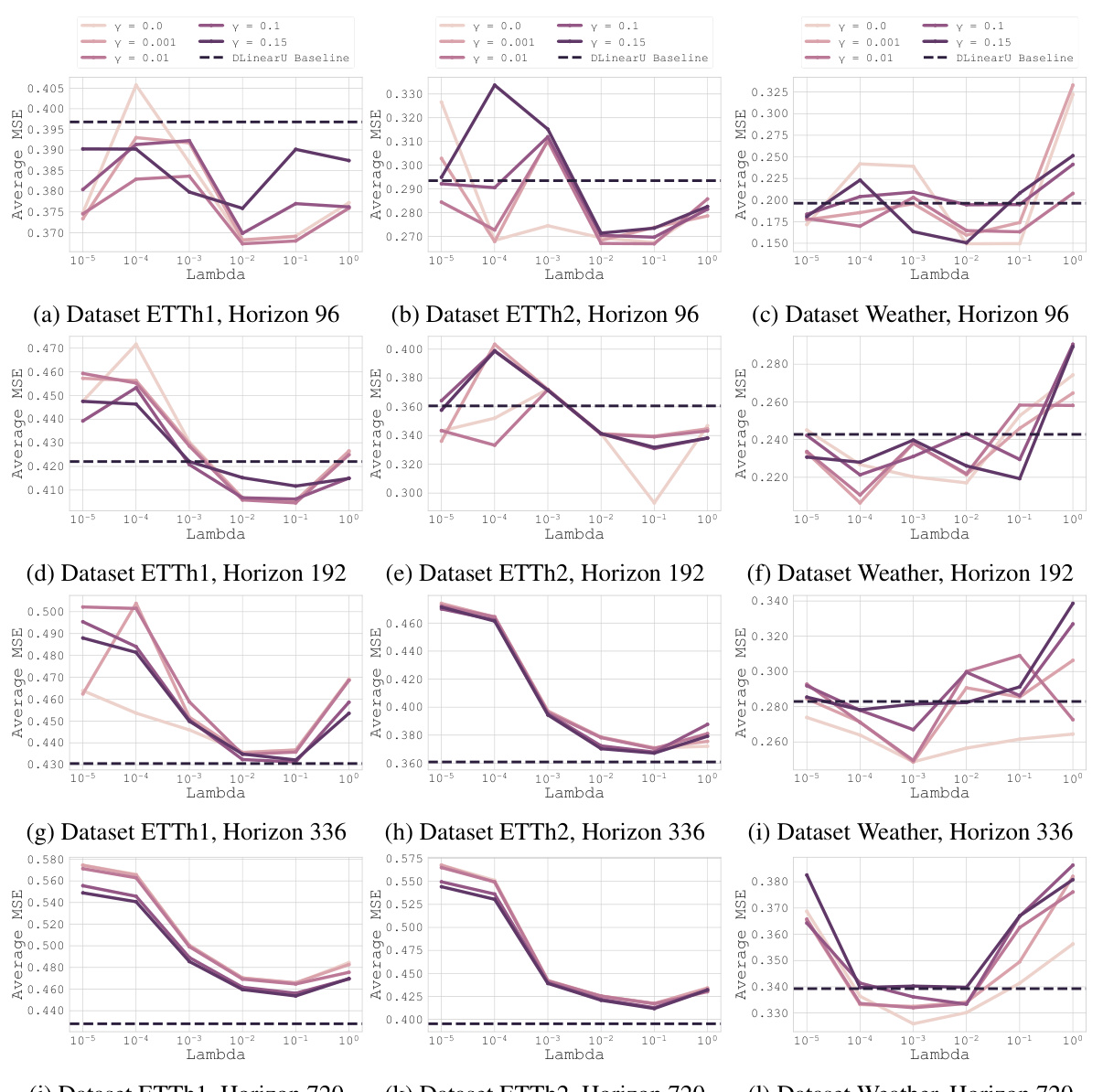
This figure shows the results of the proposed optimization method applied to the PatchTST baseline model on three different datasets (ETTh1, ETTh2, and Weather) and four different forecasting horizons (96, 192, 336, and 720). Each subfigure represents a dataset and horizon, showcasing the average mean squared error (MSE) across three different random seeds, with varying values of gamma (γ) and lambda (λ). The plot illustrates the impact of these hyperparameters on the model’s performance, allowing for the identification of optimal values that minimize error for each specific scenario.

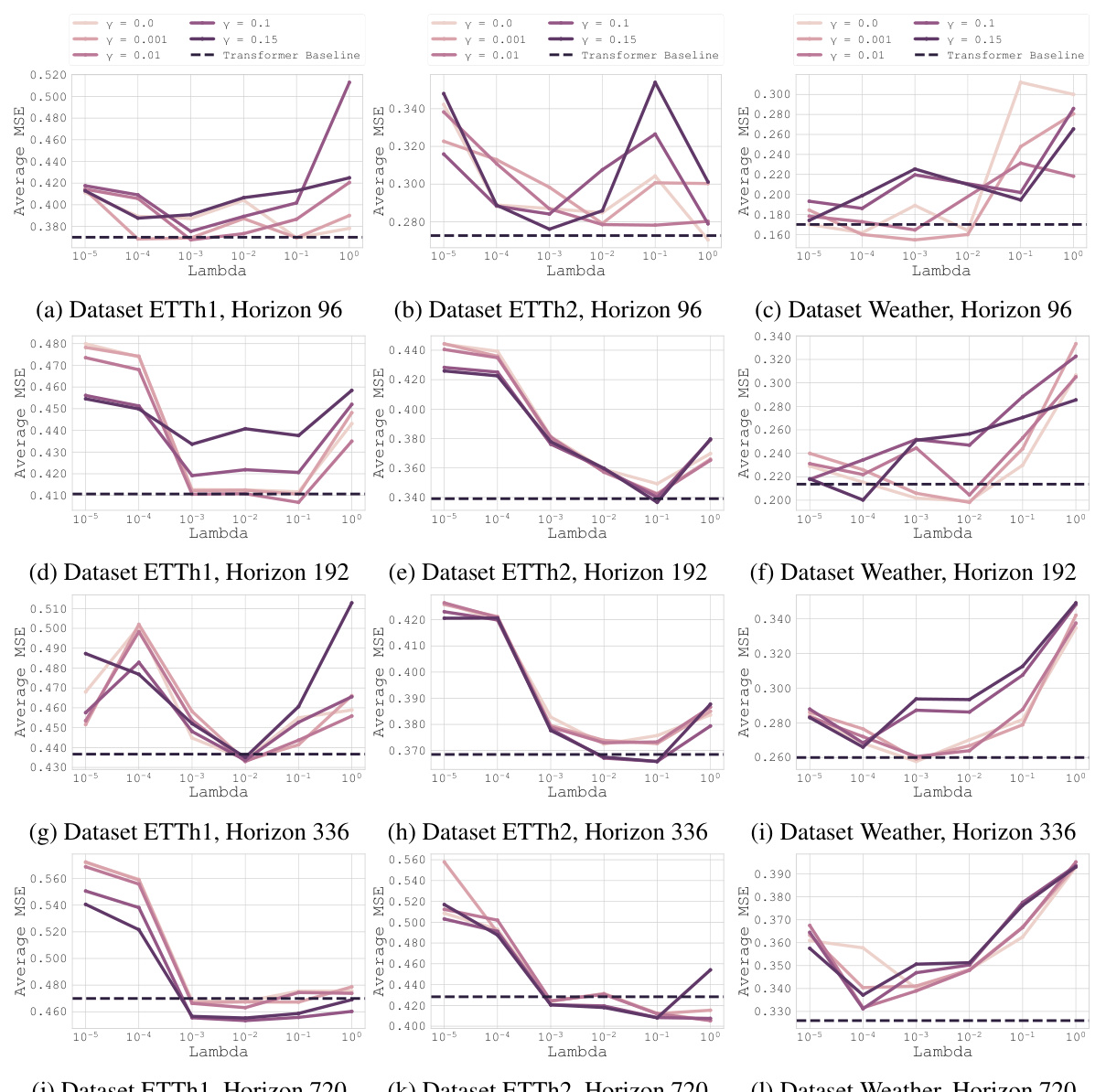
This figure visualizes the results of applying the proposed optimization method to the PatchTST baseline model. It shows the average MSE achieved across three different random seeds for various combinations of gamma (γ) and lambda (λ) hyperparameters. The results are presented separately for three datasets (ETTh1, ETTh2, Weather) and four forecast horizons (96, 192, 336, 720). Each plot allows for a comparison of performance across different values of γ and λ, aiding in the identification of optimal hyperparameter settings for each scenario.

More on tables

This table presents the results of applying multi-task learning (MTL) regularization to several univariate time series forecasting models. It compares the mean squared error (MSE) of these models with and without MTL regularization across different datasets and forecasting horizons. Statistical significance (p<0.05) is indicated using asterisks, and the best performing models for each row are highlighted in bold.

This table presents the results of applying multi-task learning (MTL) with regularization to several univariate time series forecasting models. It compares the Mean Squared Error (MSE) achieved by these models both with and without MTL regularization, and also against state-of-the-art multivariate models. The results are shown for various datasets and forecasting horizons, and statistical significance testing is used to highlight the benefits of MTL regularization.

Full paper

#