↗ OpenReview ↗ NeurIPS Proc. ↗ Chat
TL;DR#
Deep learning models often struggle to generalize to out-of-distribution (OOD) data, a major challenge for real-world applications. Existing methods mainly focus on pairwise invariances, ignoring the data’s intrinsic structure. Humans, in contrast, recognize objects by decomposing them into parts and understanding their relations.
This paper introduces Reconstruct and Match (REMA), a novel framework that captures the topological homogeneity of objects. REMA uses a selective slot-based reconstruction module to identify main components and a hypergraph-based relational reasoning module to model their high-order dependencies. Extensive experiments demonstrate that REMA significantly outperforms state-of-the-art methods on various OOD benchmarks, showcasing its effectiveness in both OOD generalization and test-time adaptation settings.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working on out-of-distribution (OOD) generalization and test-time adaptation in deep learning. It introduces a novel framework that addresses the limitations of existing methods by focusing on the topological structure of data, leading to significant improvements in model robustness. This work opens new avenues for research in unsupervised representation learning, hypergraph neural networks, and OOD robustness, impacting various applications like computer vision and autonomous driving. The framework’s interpretability is also a significant advancement, making it easier for researchers to understand the underlying mechanisms.
Visual Insights#
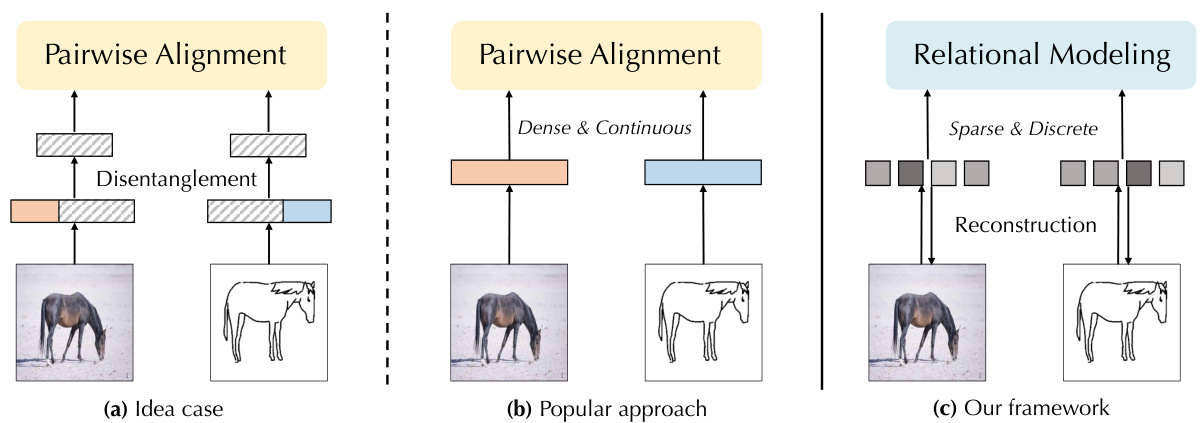
This figure illustrates the motivation behind the proposed REMA framework by comparing it to ideal and popular approaches for OOD generalization. (a) shows the ideal scenario where latent factors are perfectly disentangled into common and specific parts, allowing for easy alignment between different distributions. (b) depicts the limitations of existing methods which often work with dense, continuous latent features and directly attempt alignment without considering underlying structures. (c) highlights REMA’s novel approach, leveraging sparse, discrete ‘slots’ to represent object components, facilitating both reconstruction and relational modeling to achieve better OOD robustness.
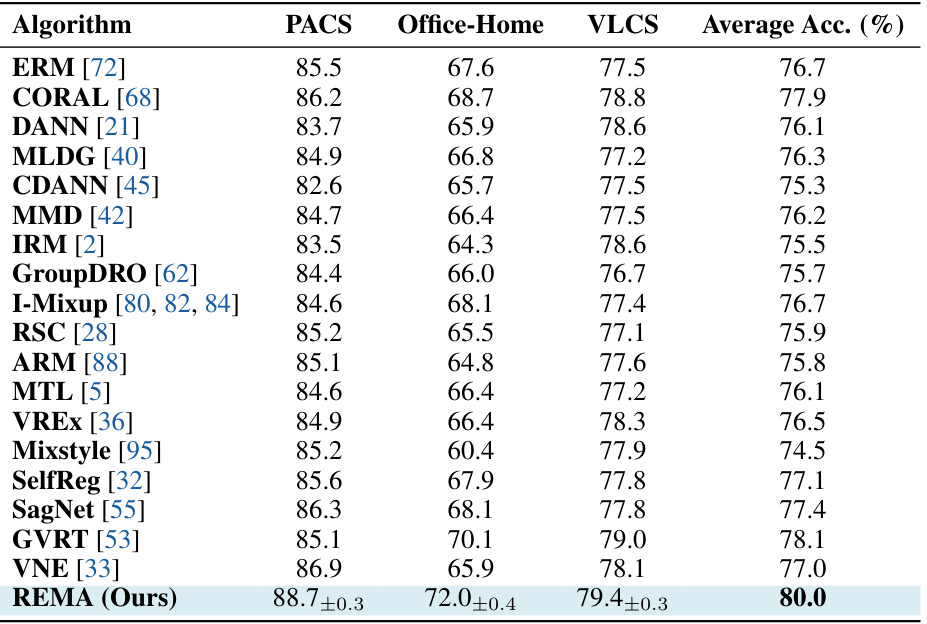
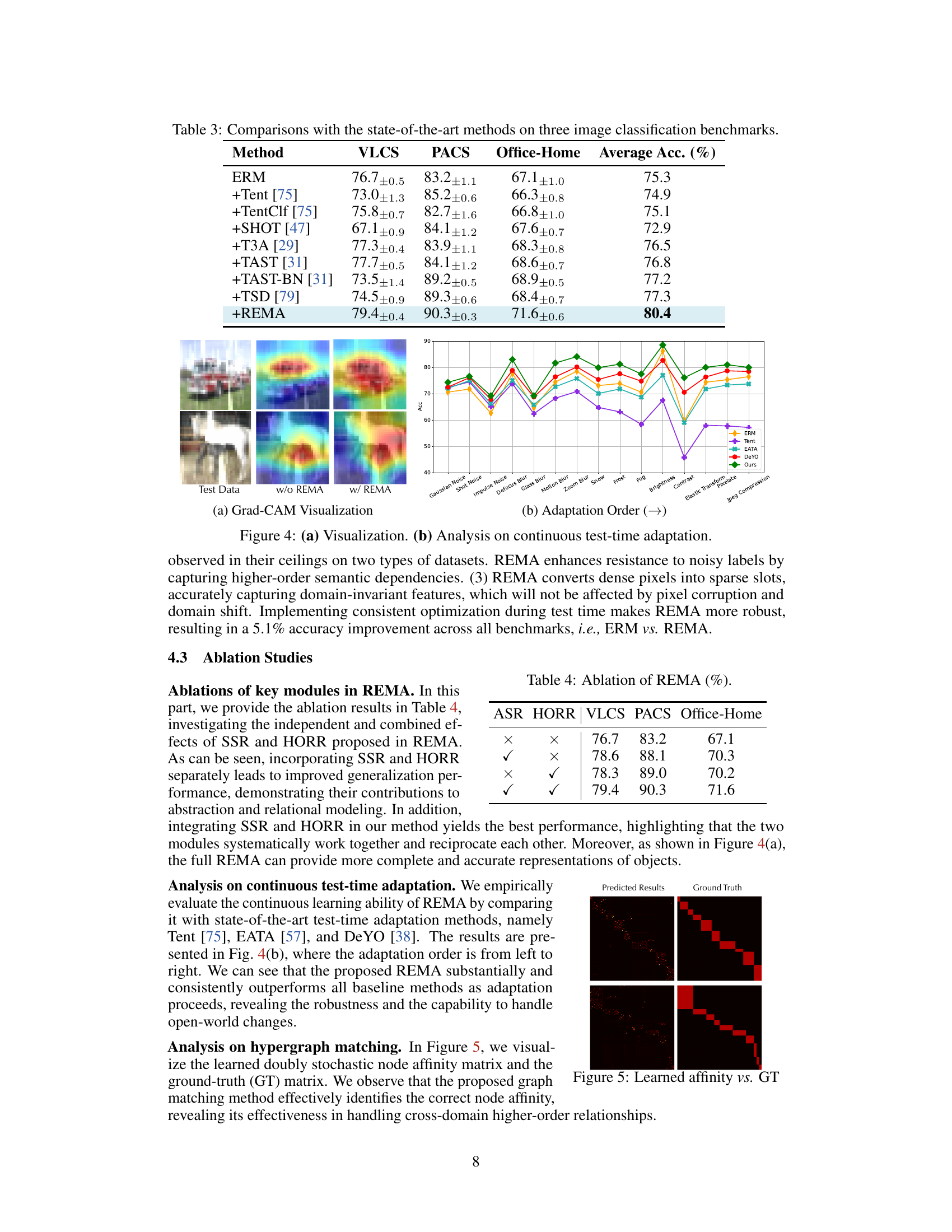
This table presents a comparison of the proposed REMA model against various state-of-the-art OOD generalization methods across three benchmark datasets: PACS, Office-Home, and VLCS. The table highlights the average classification accuracy achieved by each method on each dataset, providing a quantitative assessment of REMA’s performance relative to existing approaches. Importantly, the results shown here exclude any test-time adaptation techniques, focusing solely on the generalization capabilities of the models.
In-depth insights#
Topological Reasoning#
Topological reasoning, in the context of this research paper, likely refers to a method for analyzing object recognition that goes beyond simple pairwise comparisons of features. Instead, it focuses on the structural relationships between parts of an object. This approach mimics human perception, where we tend to decompose objects into components and analyze their arrangement. The paper likely proposes a model that captures high-order dependencies between these components, moving beyond pairwise relationships to more sophisticated representations of an object’s topological structure. This could involve techniques such as hypergraphs, which naturally encode high-order relationships, allowing the model to learn complex, structural object representations which are robust to distribution shifts. The core idea is that capturing this inherent topological homogeneity enhances the model’s ability to generalize to out-of-distribution data, providing more robust and accurate object recognition.
Slot-Based Reconstruction#
Slot-based reconstruction, a core concept in many modern object recognition systems, offers a powerful approach to disentangling complex visual information. By mapping dense pixel data into a sparse set of discrete “slots,” this method elegantly addresses the challenges of high dimensionality and redundancy in raw image data. Each slot can be viewed as a learned, abstract representation of a significant object part or feature. This allows the model to focus on the most relevant components, thus improving efficiency and robustness against noisy or irrelevant information. The unsupervised nature of slot-based reconstruction is particularly appealing, as it eliminates the need for labor-intensive manual annotation of object parts or features. This technique’s inherent sparsity promotes disentanglement, enabling the network to more effectively capture the topological relations between object components. The dynamic nature of slot allocation and assignment further enhances adaptability and generalization. This results in a more robust and interpretable model, especially in out-of-distribution scenarios where the unseen data may present novel combinations of previously learned features. Successful slot-based reconstruction ultimately hinges on the network’s ability to learn meaningful and robust slot representations that accurately capture the essential characteristics of the object. Careful consideration of factors such as the number of slots and the network architecture is critical to achieving optimal performance.
OOD Generalization#
Out-of-distribution (OOD) generalization, a critical challenge in machine learning, focuses on building models robust to unseen data distributions. Existing methods often concentrate on aligning features between known domains, neglecting the inherent structure and higher-order relationships within the data. The paper addresses this limitation by emphasizing the importance of topological homogeneity. It proposes to capture the object’s topological structure by decomposing objects into main components (slots) and then modeling high-order dependencies between these components. This approach moves beyond simple pairwise comparisons to capture richer structural information. In doing so, the method aims to mimic human object recognition, which involves identifying components and their relationships for understanding. The resulting model demonstrates improved OOD generalization, surpassing state-of-the-art methods, highlighting the importance of topological reasoning for enhanced robustness. This innovative method offers a significant advancement in the field, moving beyond existing feature alignment techniques by considering the underlying structure of data.
Test-Time Adaptation#
Test-time adaptation (TTA) addresses the challenge of deep learning models’ sensitivity to distribution shifts between training and deployment. Unlike traditional methods focusing on modifying the model during training, TTA methods leverage unlabeled data from the target domain during inference to dynamically adjust the model’s parameters or predictions. This allows for improved performance in unseen environments without retraining. A key advantage is the ability to adapt to new data without extensive retraining, which is especially valuable in real-world scenarios with ever-changing distributions. However, challenges remain, including the risk of overfitting to the limited target data and the computational cost associated with online model adaptation. Effective TTA strategies must balance the need for adaptation with the prevention of overfitting and maintain efficiency to handle real-time constraints. Recent research has focused on integrating self-supervision, leveraging auxiliary tasks to improve the generalization capabilities of the adaptation process and enhance robustness against noise.
Hypergraph Matching#
Hypergraph matching, in the context of the provided research paper, is a crucial technique for modeling high-order relationships within data. Unlike traditional graph matching which focuses on pairwise interactions, hypergraph matching extends this capability to model relationships between multiple entities simultaneously. This is particularly powerful in scenarios where complex interdependencies exist, such as in object recognition where the object is decomposed into several parts. The ability to capture these high-order relationships through hypergraphs allows the model to learn more intricate and robust representations. By representing object components as nodes and their interdependencies as hyperedges, the model can capture the topological homogeneity of objects, improving out-of-distribution generalization. The use of a hypergraph neural network (HGNN) for hypergraph learning allows efficient message-passing and feature aggregation across the hypergraph structure, further enhancing the representation learning. The Sinkhorn layer is then leveraged to align the hypergraphs across different domains (e.g., training and test datasets), facilitating robust generalization and adaptation. In essence, hypergraph matching provides a powerful framework to move beyond pairwise relationships and model the intricate relationships needed for complex object representation and robust generalization.
More visual insights#
More on figures
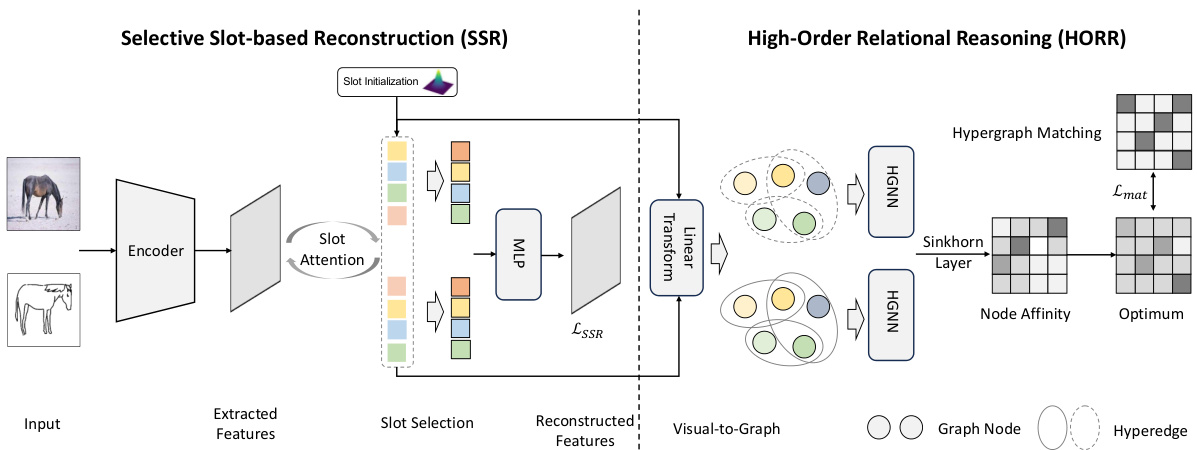
This figure illustrates the Reconstruct and Match (REMA) framework, which is the core methodology of the paper. It shows the two main modules: Selective Slot-based Reconstruction (SSR) and High-Order Relational Reasoning (HORR). SSR extracts key components (slots) from the input image. HORR then models the relationships between these components using a hypergraph to capture high-order dependencies, achieving topological homogeneity. The figure depicts the data flow, showing the input image, feature extraction, slot attention, slot selection, reconstruction, and hypergraph reasoning steps. The final output is a representation that integrates both low and high-order relationships between the image components for object recognition.

This figure presents an overview of the Reconstruct and Match (REMA) framework, highlighting its two main modules: Selective Slot-based Reconstruction (SSR) and High-Order Relational Reasoning (HORR). SSR is depicted as taking dense image pixels and converting them into a sparse set of slot vectors that represent the main components of an object. HORR then takes these slots and creates a hypergraph to model the high-order relationships between these components (slots), aiming to capture the topological homogeneity of the objects. The hypergraph is processed using a Hypergraph Neural Network (HGNN) before generating a final result.

This figure compares the performance of ERM and REMA on CIFAR-10C, a dataset with various image corruptions, using the CIFAR-10 dataset as the source domain. It visually demonstrates the improved robustness and generalization capabilities of the proposed REMA model compared to the standard ERM approach across different types of image corruptions. Each bar represents a specific type of corruption (e.g., Gaussian Noise, Shot Noise, etc.) and the height of each bar indicates the accuracy achieved by each method on that corruption type. REMA consistently shows higher accuracy across all corruption types, highlighting its effectiveness in handling out-of-distribution data.

The figure shows two parts. (a) Grad-CAM Visualization: It visualizes the attention weights of the REMA model, highlighting the regions of the image that are most relevant to the prediction. It shows how REMA focuses on different parts of the object, enabling it to improve the overall performance. (b) Adaptation Order: It shows how the average accuracy of different test-time adaptation methods changes as the number of adaptation steps increases. It shows how REMA consistently outperforms other methods.
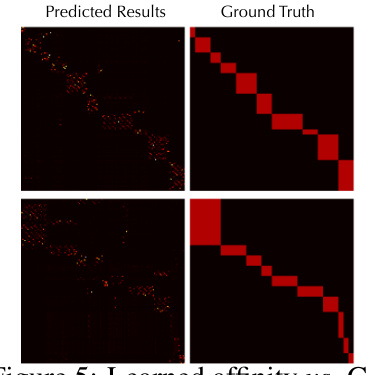
This figure visualizes the learned affinity matrix and the ground truth (GT) matrix. The learned affinity matrix is produced by the hypergraph matching module of REMA, which models high-order topological relations. The visualization helps assess the model’s ability to accurately capture the structural similarities between objects across different domains. The top row shows the predicted affinity, while the bottom row shows the ground truth. The dark and bright colors represent low and high affinity values, respectively. Ideally, the learned affinity matrix should closely resemble the GT matrix, indicating effective matching.

This figure visualizes the feature embeddings obtained by different methods, namely ERM, REMA without SSR, REMA without HORR, and the full REMA model. The visualization uses t-SNE to project the high-dimensional feature embeddings into a 2D space, allowing for visualization of the data clustering. Different colors represent different classes in the CIFAR-10C dataset with snow corruption. The figure demonstrates how the proposed REMA model, with both SSR and HORR modules, leads to better-clustered feature embeddings compared to the baselines. The absence of either SSR or HORR leads to reduced data separability.
More on tables
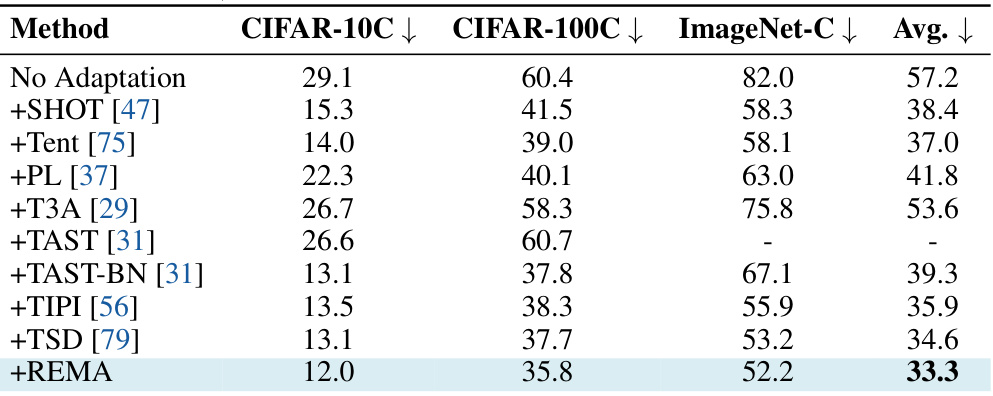
This table presents a comparison of the proposed REMA method against several state-of-the-art test-time adaptation methods. The comparison is based on the average error rate (%) achieved on three image corruption benchmark datasets (CIFAR-10C, CIFAR-100C, and ImageNet-C). A lower error rate indicates better performance. All methods used a ResNet-50 backbone for fair comparison. The testing was performed at the highest level of image corruption for each dataset.

This table presents the ablation study results for the REMA framework. It shows the impact of using the Selective Slot-based Reconstruction (SSR) and High-Order Relational Reasoning (HORR) modules individually and together on the performance of the model across three benchmark datasets: VLCS, PACS, and Office-Home. The results demonstrate that both modules contribute to improved generalization performance, and that combining them yields the best overall results.
Full paper#