Trajectory Flow Matching with Applications to Clinical Time Series Modelling

↗ OpenReview ↗ NeurIPS Proc. ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is important because it introduces a novel simulation-free training method for Neural Stochastic Differential Equations (Neural SDEs), addressing the scalability and stability challenges of existing approaches. This is highly relevant to researchers working with complex time series data, particularly in fields like healthcare, where efficient and accurate modeling of stochastic and irregular processes is crucial. The proposed Trajectory Flow Matching method is particularly significant for researchers working with clinical time-series data because it improves performance and uncertainty prediction which is a crucial parameter in that setting. The method opens avenues for building more complex models of clinical time series and could be used for more accurate and informative disease risk prediction.

Visual Insights

#

This figure illustrates the Trajectory Flow Matching (TFM) method. TFM simultaneously learns two neural networks: one that estimates the next time point in a time series (x1), given the previous points and covariates (xto, xt-1, xt-2, c); and another that estimates the uncertainty associated with this prediction (σo(t,xt)). The prediction of the next time point is conditioned on previous observations and contextual variables. The figure highlights how these estimations are combined to provide both a point prediction and an uncertainty range, which is crucial for applications involving noisy and irregularly sampled data.

This table presents the Mean Squared Error (MSE) results for various time series models applied to four different datasets (ICU Sepsis, ICU Cardiac Arrest, ICU GIB, ED GIB). The models are categorized into deterministic and stochastic types. The MSE values are reported as mean ± standard deviation (×10−3). The table highlights the best-performing model for each dataset and model type.

In-depth insights

#

TFM: A New Approach

#

The proposed Trajectory Flow Matching (TFM) offers a novel, simulation-free method for training neural stochastic differential equations (Neural SDEs). Unlike traditional Neural SDE training, which relies on computationally expensive backpropagation through the SDE dynamics, TFM leverages flow matching techniques from generative modeling to bypass this limitation. This approach enhances both the scalability and stability of Neural SDE training significantly. The core innovation lies in its ability to directly match the marginal distributions of the target time series using a cleverly constructed loss function, thereby obviating the need for explicit SDE simulation. While the paper presents theoretical underpinnings to support TFM’s capability to accurately learn data couplings in time-series data, a key aspect of the proposed method is its successful application to irregularly sampled clinical time series. This shows great promise in improving real-world applications, particularly where traditional SDE models struggle.

Clinical Data Modeling

#

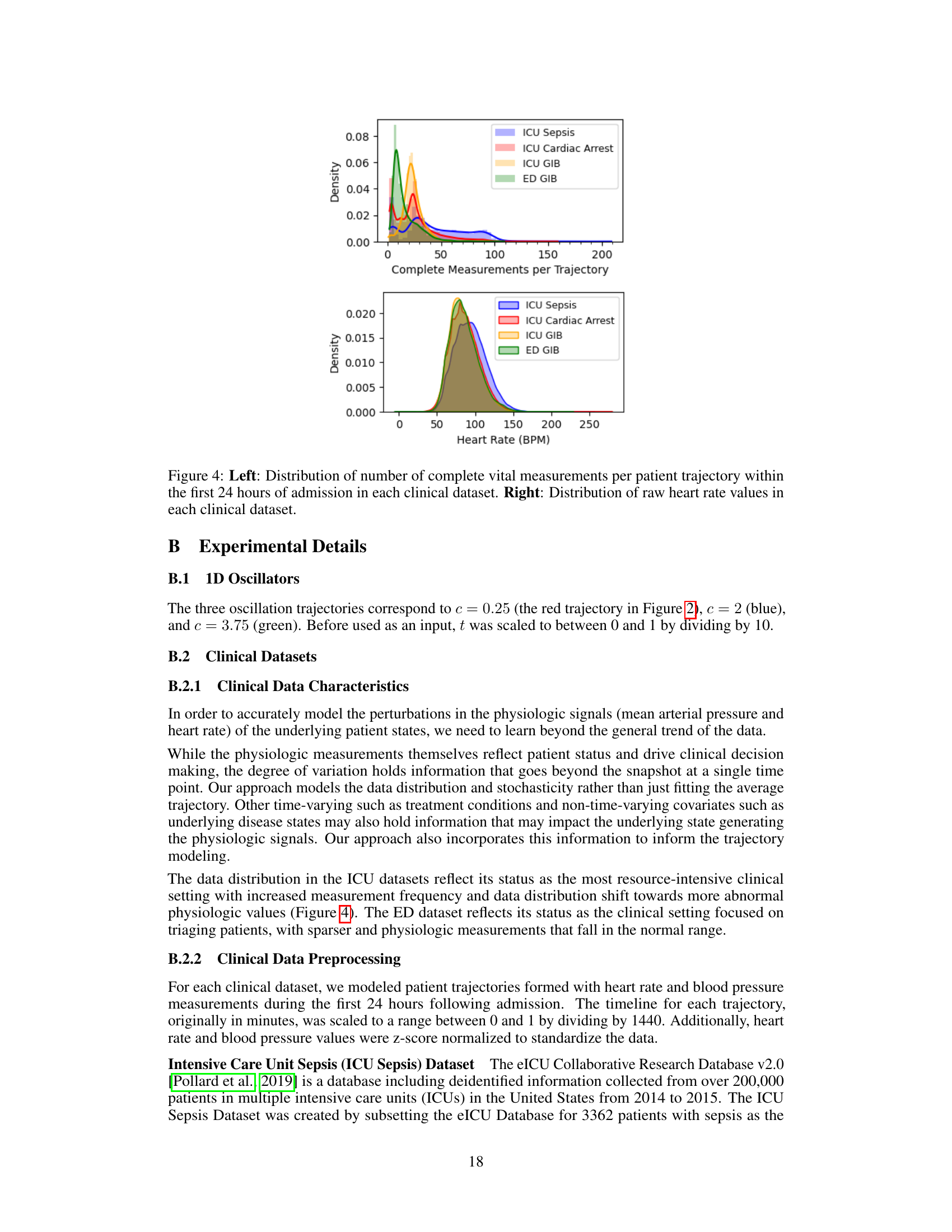
Clinical data modeling presents unique challenges due to the irregularity and noise inherent in real-world patient data. The paper addresses these by proposing a novel approach, Trajectory Flow Matching (TFM), that leverages stochastic differential equations (SDEs). Unlike traditional methods relying on backpropagation through the SDE dynamics, TFM employs a simulation-free technique based on flow matching. This improves scalability and stability, particularly crucial for high-dimensional clinical data. The focus on accurately modeling uncertainty is highlighted as vital in clinical settings, where precise prediction and reliable confidence intervals are critical for informed decision-making. The paper validates the approach using multiple clinical datasets, demonstrating improved accuracy and uncertainty estimation compared to existing state-of-the-art methods. A key advantage is its ability to handle irregularly sampled data, a common feature of real-world clinical time series. The successful application of TFM to diverse datasets suggests the robustness of the approach, making it promising for future applications in clinical decision support.

Coupling Preservation

#

The concept of “Coupling Preservation” in the context of time series modeling using stochastic differential equations is crucial for accurately capturing the inherent relationships between data points across time. The core idea is to ensure that the model’s learned dynamics faithfully reproduce the dependencies observed in the real-world data. Failure to preserve these couplings can lead to inaccurate predictions, especially when dealing with irregularly sampled or complex trajectories. The authors address this by proposing conditions under which simulation-free training of continuous-time dynamics is possible while maintaining the integrity of the couplings. This simulation-free approach is crucial for scalability and training stability, which are significant challenges in the training of traditional Neural SDE models. The proposed Trajectory Flow Matching (TFM) method is designed to learn these dynamics without the need for time-consuming backpropagation, representing a significant improvement in both efficiency and robustness. The presented theoretical guarantees provide confidence that TFM’s simulation-free training does not compromise the essential inter-temporal connections of the data, ensuring its suitability for applications demanding high accuracy in modeling complex temporal patterns.

Uncertainty Estimation

#

In many real-world applications, especially those involving time-series data, uncertainty estimation is critical for reliable decision-making. This paper addresses this by proposing a novel method, Trajectory Flow Matching (TFM), which leverages flow matching techniques to learn SDEs representing time-series. A key advantage is the simulation-free training; this bypasses the challenges of backpropagation through the SDE dynamics, significantly enhancing scalability and stability. TFM also incorporates uncertainty prediction within its framework, allowing for not only point estimates but also quantifications of confidence in the model’s predictions. The method’s application to clinical time series data showcases improved performance over baseline methods, demonstrating its effectiveness in real-world scenarios where precise uncertainty estimates are crucial. The novel reparameterization trick further stabilizes training. The empirical results on various clinical time series show that the proposed method demonstrates improved accuracy and uncertainty prediction compared to several other methods.

Future Work Directions

#

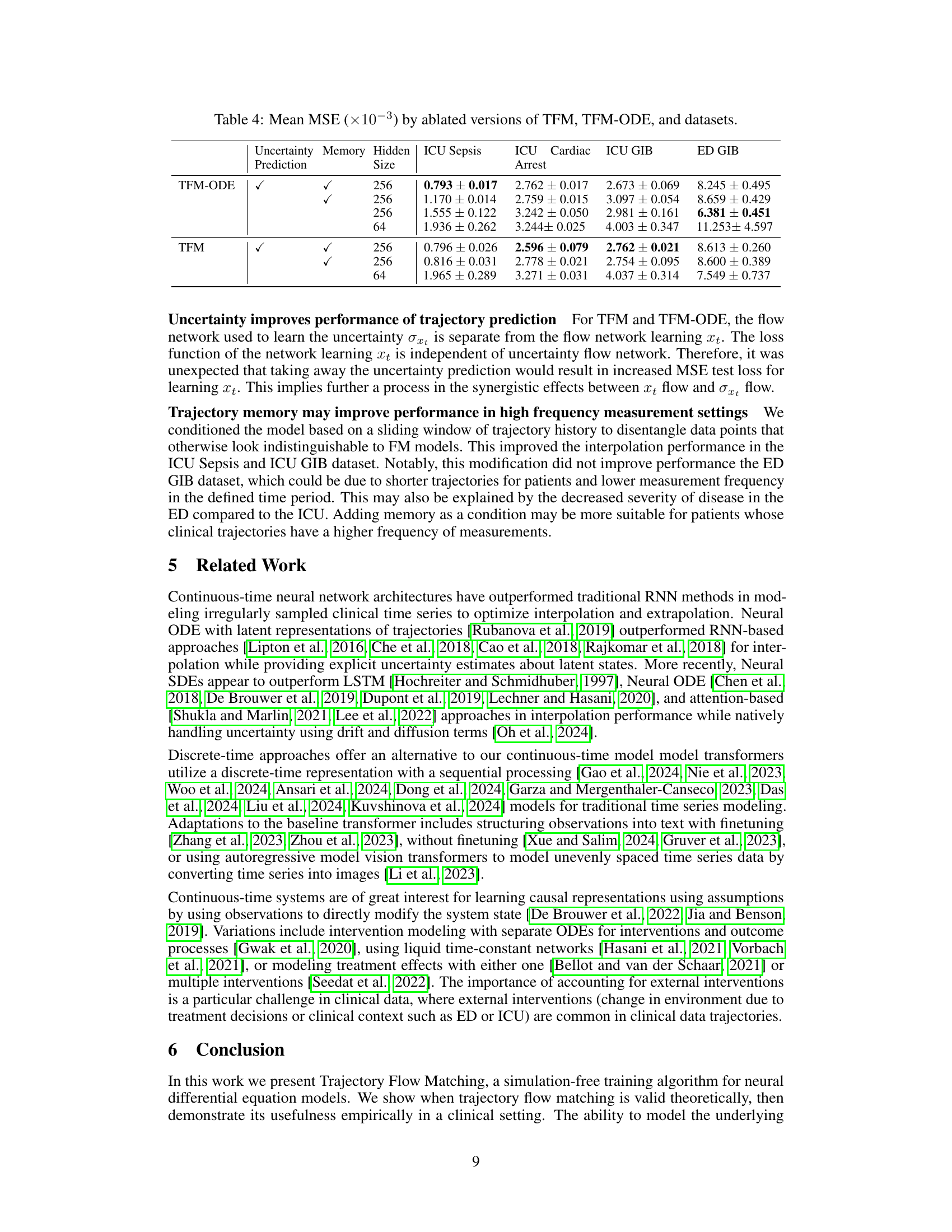
Future research could explore several promising avenues. Extending the Trajectory Flow Matching (TFM) framework to handle higher-order derivatives would enhance its ability to model complex systems with intricate interactions. Incorporating more sophisticated uncertainty quantification methods could improve the reliability of predictions, particularly in high-stakes clinical settings. Investigating the use of different neural network architectures beyond the current choice is warranted, as this could potentially improve model performance and efficiency. Furthermore, exploring causal inference techniques within the TFM framework would unlock the ability to model interventions and their effects more accurately. Finally, applying TFM to a wider range of clinical datasets and other real-world time series problems is crucial for validating its generalizability and identifying areas for improvement.

More visual insights

#

More on figures

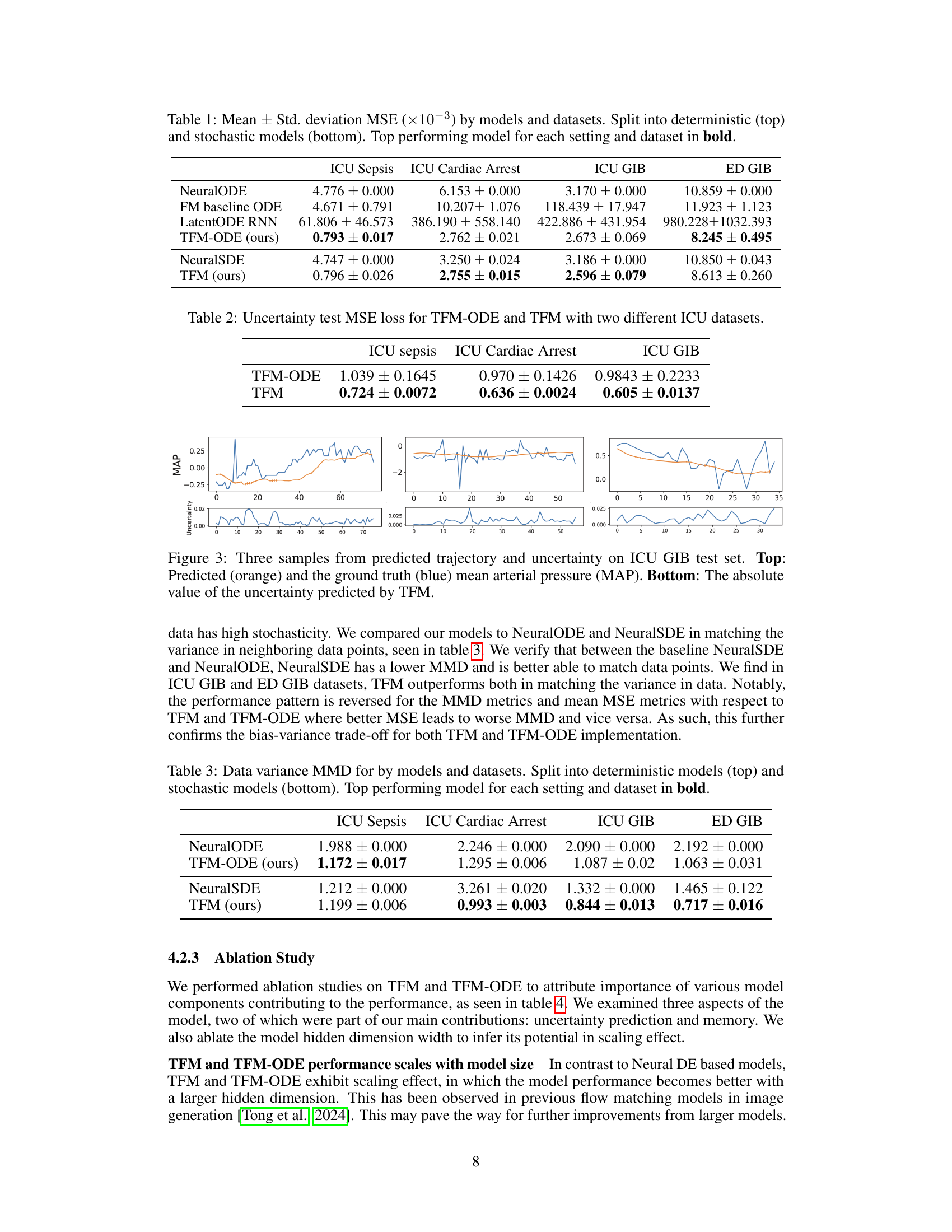
This figure compares the performance of three different models on a 1D harmonic oscillator task. The models are: TFM-ODE with memory, TFM-ODE without memory, and Aligned FM. The x-axis represents time, and the y-axis represents the oscillator’s position. The figure shows that TFM-ODE with memory is able to fit the data much better than the other two models, especially in regions where the trajectories intersect.

This figure compares the performance of three different models on a 1D harmonic oscillator task where trajectories cross each other. The left panel shows the results of TFM-ODE with a memory of 3, demonstrating its ability to accurately predict the crossing trajectories. The middle panel shows the results of TFM-ODE without memory, highlighting the importance of memory in capturing trajectory interactions. The right panel shows the performance of Aligned FM, illustrating that it struggles to accurately model the crossing trajectories.

This figure compares the performance of three different models on a 1D harmonic oscillator task. The task involves predicting the trajectory of a damped harmonic oscillator with varying damping coefficients, resulting in intersecting trajectories. The left panel shows the results of the proposed TFM-ODE model with memory (i.e., using past observations in the prediction), demonstrating accurate prediction of the intersecting trajectories. The middle panel shows the same model without memory, which fails to accurately predict the trajectories. The right panel shows the performance of a baseline Aligned FM model, which also fails to correctly predict the intersecting trajectories. The figure demonstrates the importance of memory in accurately predicting complex, intersecting trajectories in time-series data.

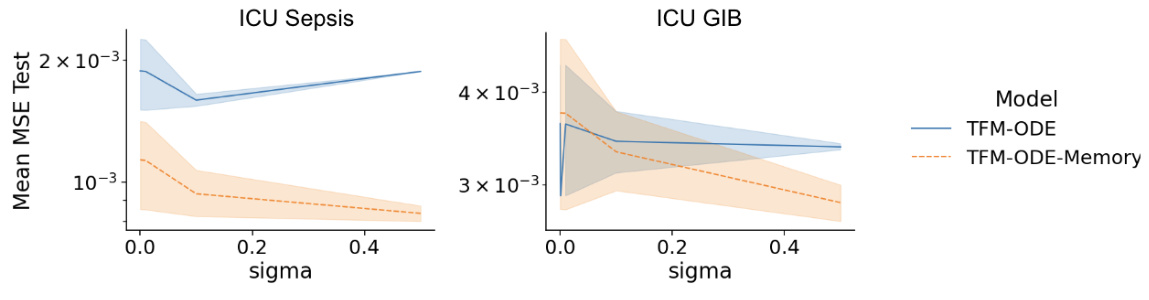
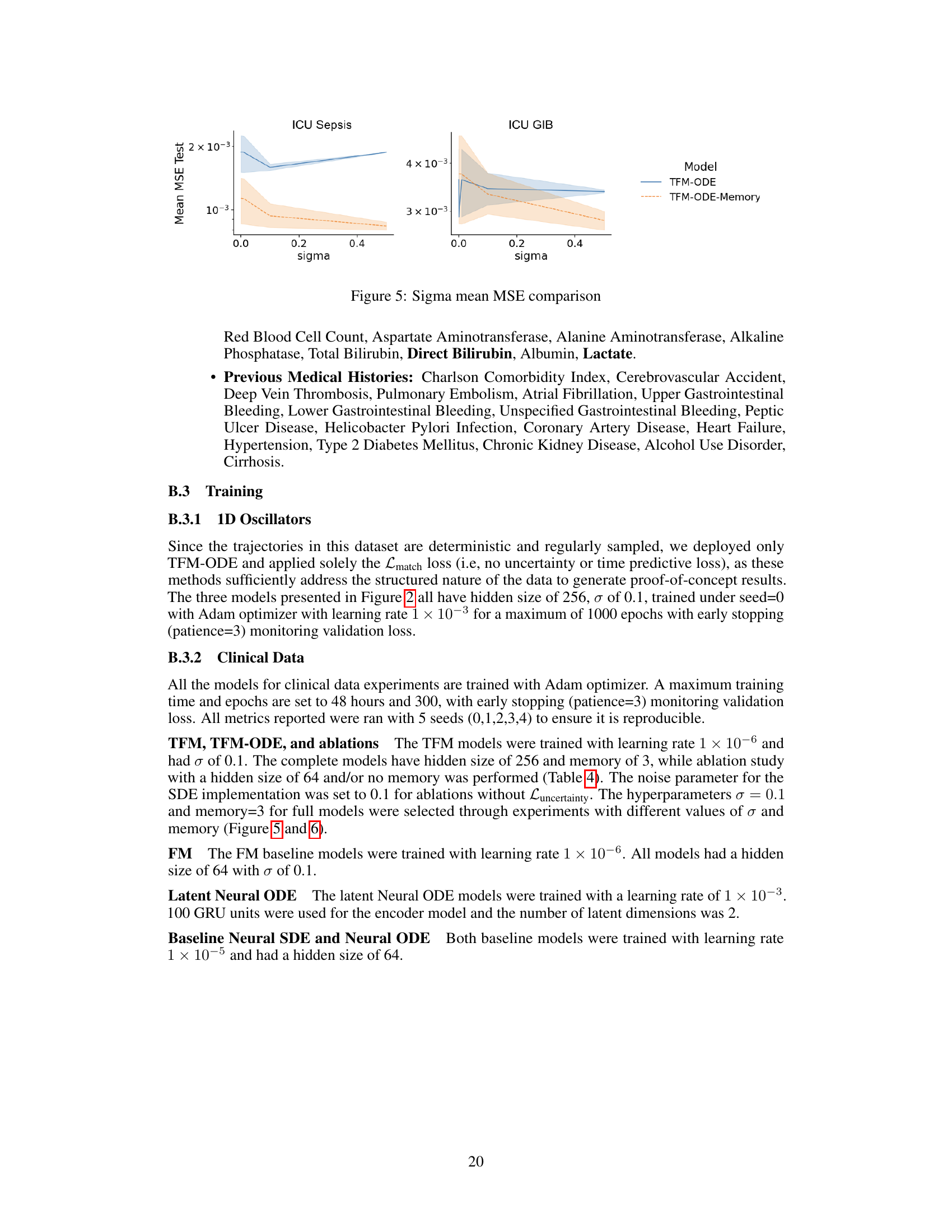
This figure shows the comparison of mean squared error (MSE) for different sigma values on ICU Sepsis and ICU GIB datasets. The x-axis represents the sigma values, while the y-axis represents the mean MSE test. Two models are compared: TFM-ODE and TFM-ODE with memory. The shaded region indicates the standard deviation of the MSE across multiple runs. This figure helps illustrate the impact of varying sigma (noise parameter) and using memory (past observations) on model performance for different datasets.

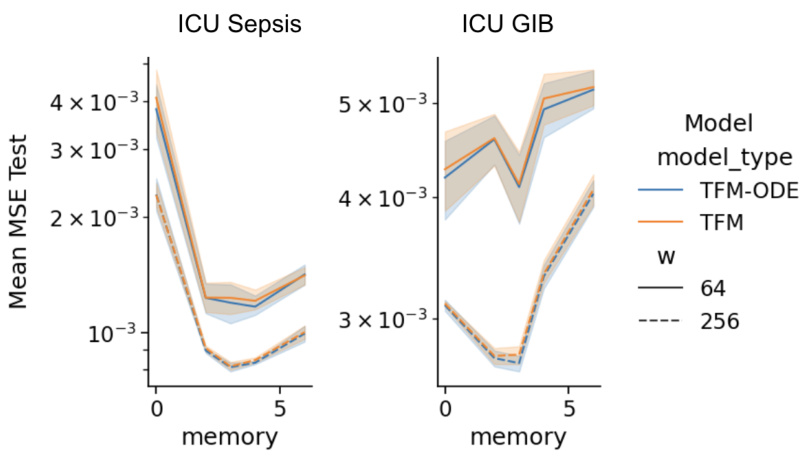
The figure compares the mean squared error (MSE) for different values of sigma (σ) for two different models, TFM-ODE and TFM. The results are shown for two different datasets: ICU Sepsis and ICU GIB. It examines the impact of the noise parameter (sigma) on model performance. Each line represents a model with either 64 or 256 hidden units.

More on tables

This table presents the uncertainty test MSE loss for both TFM-ODE and TFM models across two different ICU datasets (ICU Sepsis and ICU Cardiac Arrest). It shows the mean and standard deviation of the MSE loss for each model and dataset, highlighting the difference in uncertainty prediction performance between TFM-ODE and TFM.

This table presents the Maximum Mean Discrepancy (MMD) results, a metric measuring the similarity between the predicted and true distributions of the next observation in the time series. The results are separated into deterministic (top) and stochastic (bottom) models. The table compares the performance of several models (NeuralODE, TFM-ODE, NeuralSDE, and TFM) across four different datasets (ICU Sepsis, ICU Cardiac Arrest, ICU GIB, and ED GIB), highlighting the top-performing model for each dataset and model type.

This table presents the Mean Squared Error (MSE) achieved by different models (deterministic and stochastic) on four different datasets. The MSE is a measure of the difference between the model’s predictions and the actual values. Lower MSE indicates better performance. The table is split into two sections: deterministic models and stochastic models, with the best performing model for each dataset highlighted in bold. The results allow for a comparison of the performance of various models for time series prediction in different contexts.

Full paper

#