Compositional Generalization Across Distributional Shifts with Sparse Tree Operations

↗ OpenReview ↗ NeurIPS Proc. ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial for researchers in natural language processing and artificial intelligence due to its novel approach to compositional generalization. It offers a more efficient and flexible neurosymbolic architecture that addresses the limitations of existing methods, potentially impacting future work on robust and scalable AI systems. The introduction of Sparse Coordinate Trees (SCT) and improvements to the Differentiable Tree Machine (DTM) provide researchers with valuable tools and insights for advancing the field.

Visual Insights

#

This figure compares the generalization performance of the proposed Sparse Differentiable Tree Machine (sDTM) model against several baselines across various out-of-distribution scenarios. The baselines include a standard Transformer, a Relative Universal Transformer, and NQG (a hybrid neurosymbolic model). The different generalization scenarios tested are: IID (in-distribution), 0-Shot Lexical (seeing a word only once during training), 1-Shot Lexical (seeing a word once in the training data), Length/Structural (generalizing to sequences longer than those seen during training), MCD (maximum compound divergence, which means similar unigram distributions but vastly different n-gram frequencies), and Template (holding back abstract n-grams from training). The figure visualizes the relative performance of each model across these scenarios, allowing for a comprehensive evaluation of their generalization abilities.

This table presents the performance comparison of different models on the Active-Logical task, comparing in-distribution (IID) and out-of-distribution (OOD) generalization abilities. The models compared are a standard Transformer, a Relative Universal Transformer, NQG (a hybrid neurosymbolic model), the original Differentiable Tree Machine (DTM), and the proposed Sparse Differentiable Tree Machine (sDTM) with and without pruning. The table shows accuracy scores for each model and dataset split (IID, 0-shot lexical, structural), along with the parameter count and memory usage. It highlights the significant improvement of sDTM in terms of efficiency (parameter count and memory usage) without sacrificing accuracy compared to DTM and other models.

In-depth insights

#

Sparse Tree Power

#

The concept of “Sparse Tree Power” suggests a paradigm shift in how tree-structured data is processed and represented, especially within machine learning contexts. Sparsity, by reducing computational complexity and memory requirements, is key. It allows for efficient handling of large, deep trees often encountered in natural language processing (NLP) and other areas. The “power” likely refers to enhanced capabilities stemming from efficient processing. This could include improved generalization abilities, particularly in handling compositional tasks; better scalability to deal with increasingly complex tree structures; and potentially, faster training and inference times. The approach likely leverages advanced algorithms to perform operations on sparse trees directly, avoiding unnecessary computations associated with dense representations. This efficiency empowers applications that were previously computationally infeasible due to the memory and processing limitations of dense tree structures. The combination of sparsity and efficient algorithms is the core of the “Sparse Tree Power” idea.

Unified Neuro-Symbolic

#

The concept of “Unified Neuro-Symbolic” AI systems represents a significant shift from traditional hybrid approaches. Instead of treating neural networks and symbolic reasoning as separate, interacting modules, a unified approach aims to integrate both paradigms seamlessly within a single computational framework. This integration could leverage the strengths of both: neural networks’ ability to learn complex patterns from data and symbolic reasoning’s capacity for explicit knowledge representation and logical inference. A key challenge is developing suitable representations that allow for fluid transitions between the continuous nature of neural activations and the discrete structure of symbolic expressions. Successful unified models are expected to exhibit improved compositional generalization, a crucial aspect of human intelligence that remains elusive for many current AI systems. Sparse representations, as explored in the paper, provide a potential pathway towards efficient and scalable implementation of such unified models, addressing the longstanding issues of scalability and flexibility associated with traditional symbolic approaches. The integration offers the prospect of creating robust, generalizable AI that bridges the gap between data-driven learning and knowledge-based reasoning.

Compositional Generalization

#

Compositional generalization, the ability of a model to understand and generate novel combinations of previously seen components, remains a significant challenge in AI. While neural networks excel at pattern recognition, they often struggle with unseen combinations of words or concepts. This paper investigates hybrid neurosymbolic approaches, which combine the scalability of neural networks with the compositional structure of symbolic systems, to achieve improved compositional generalization. A key contribution is the introduction of Sparse Coordinate Trees (SCTs), an efficient representation for trees in vector space, enabling parallelized tree operations. By unifying symbolic and neural computation within a single framework (Sparse Differentiable Tree Machine or sDTM), this approach overcomes limitations of previous hybrid systems. The results demonstrate the efficacy of sDTM in handling various out-of-distribution shifts, showcasing its capacity for robust generalization across different datasets and tasks. However, the paper acknowledges that despite the unified approach, challenges persist with certain types of generalization, suggesting that further research is needed to fully address the complexities of compositional generalization in AI.

Seq2Seq Tree Extension

#

The concept of a ‘Seq2Seq Tree Extension’ in a research paper likely refers to adapting sequence-to-sequence (seq2seq) models, typically used for tasks involving sequential input and output (like machine translation), to operate with tree-structured data. This extension is motivated by the inherent compositional structure found in many real-world problems, especially in natural language processing, where sentences can be parsed into tree-like structures representing grammatical relationships. A core challenge is effectively mapping sequential input/output to hierarchical tree representations and vice versa. The paper likely explores various techniques for this, potentially including methods to efficiently encode tree structures into vector representations compatible with seq2seq models, and developing novel neural network architectures or modifications to existing seq2seq models for handling tree-structured data. Successful application may demonstrate improved generalization capabilities over traditional seq2seq approaches by explicitly incorporating the compositional nature of the data. The efficiency of encoding and processing tree structures within the model’s framework would be another key factor analyzed, possibly comparing it to methods directly operating on sequences without explicit tree representations.

Scalability & Limits

#

A crucial aspect of any machine learning model, especially those tackling complex tasks like natural language processing, is its scalability. The Sparse Differentiable Tree Machine (sDTM), while showing promise in compositional generalization, faces inherent scalability challenges. The original DTM’s reliance on Tensor Product Representations (TPRs) led to exponential memory growth with tree depth, severely limiting its application to larger datasets or more complex structures. sDTM’s use of Sparse Coordinate Trees (SCT) mitigates this issue to some extent, allowing for efficient representation of sparse trees. However, even with SCT, the model’s ability to scale to very deep trees or extremely large datasets remains constrained, as demonstrated by its inability to handle the FOR2LAM dataset without significant modifications. The study highlights a trade-off between computational efficiency and the capacity to address large-scale problems; this is a common limitation in neurosymbolic approaches. While sDTM demonstrates improved performance over other models, especially in handling compositional generalization, addressing scalability concerns would significantly enhance its wider applicability and usefulness for real-world applications. Future research should explore more sophisticated tree representations, potentially integrating hierarchical structures or more effective memory management techniques, to overcome these limitations. Ultimately, addressing scalability is crucial for advancing neurosymbolic techniques and making them practical solutions for complex real-world tasks.

More visual insights

#

More on figures

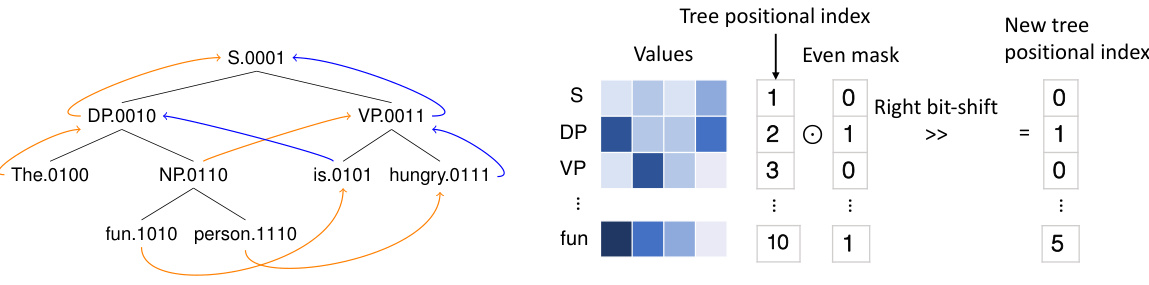
This figure illustrates how Sparse Coordinate Trees (SCT) represent a tree structure using a sparse vector encoding. Each node in the tree (e.g., ‘The’, ‘fun’, ‘person’) is associated with an N-dimensional vector (the ‘Values’). Instead of explicitly representing every position in the tree, SCT only stores vectors for the existing nodes. The ‘Tree positional index’ column shows the integer representation of each node’s position within the tree. This approach improves efficiency by avoiding the storage of zero-valued vectors for missing children nodes.

This figure demonstrates the Sparse Coordinate Trees (SCT) representation and the ’left’ and ‘right’ tree operations. The left panel shows a tree structure and how the left and right operations shift the tree structure. The right panel shows the effect of the left operation: it shifts the tree structure to the left resulting in DP becoming the root. Indices (representing tree positions) with value 0 are discarded during the operation. This illustrates the core mechanism of how tree manipulations are performed efficiently and differentiably in the Sparse Differentiable Tree Machine (sDTM).

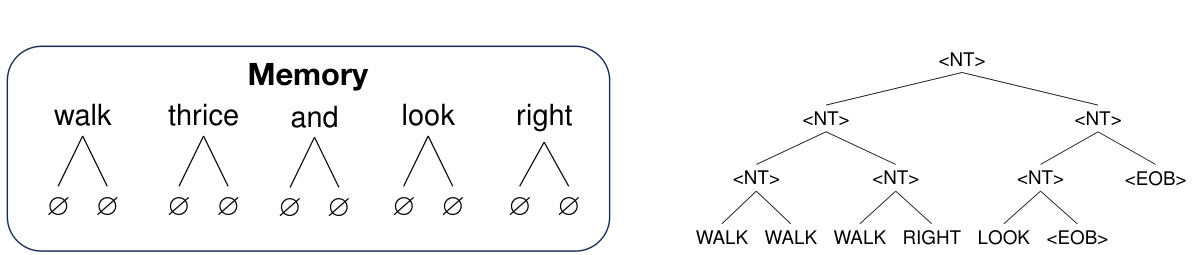
This figure illustrates how the Sparse Differentiable Tree Machine (sDTM) handles sequential inputs and outputs in a sequence-to-sequence (seq2seq) task. The left panel shows the initial memory state, where each input token is represented as a separate tree with only a root node. The right panel shows how an output sequence is converted into a tree structure using the left-aligned uniform-depth (LAUD) approach. This method simplifies the processing of sequences by structuring them as trees for easier handling by the sDTM.

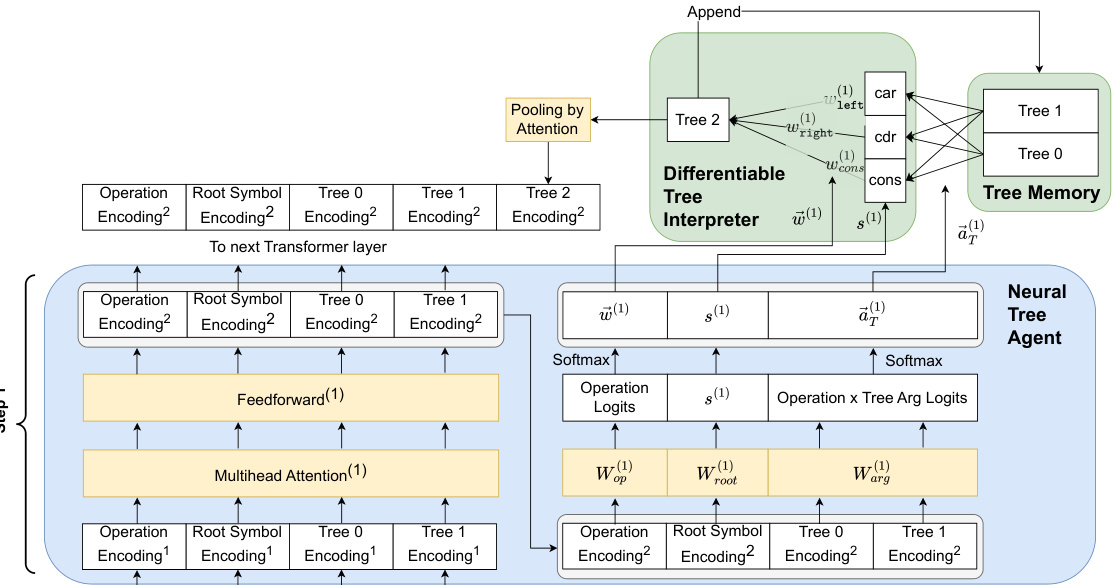
This figure illustrates one step in the Differentiable Tree Machine (DTM) process, showing how the agent, interpreter, and tree memory interact. The agent, using a transformer encoder, processes information to determine which tree operations to perform (left, right, or cons). The interpreter then executes these operations, updating the tree memory. The updated tree memory and operation information is then encoded and passed back to the agent for the next step in the process. The diagram highlights the learnable parameters within the model.

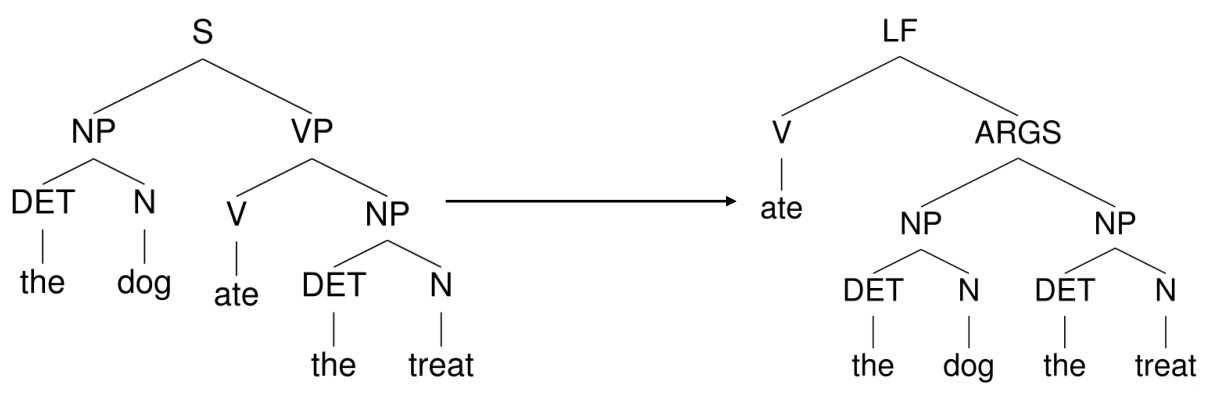
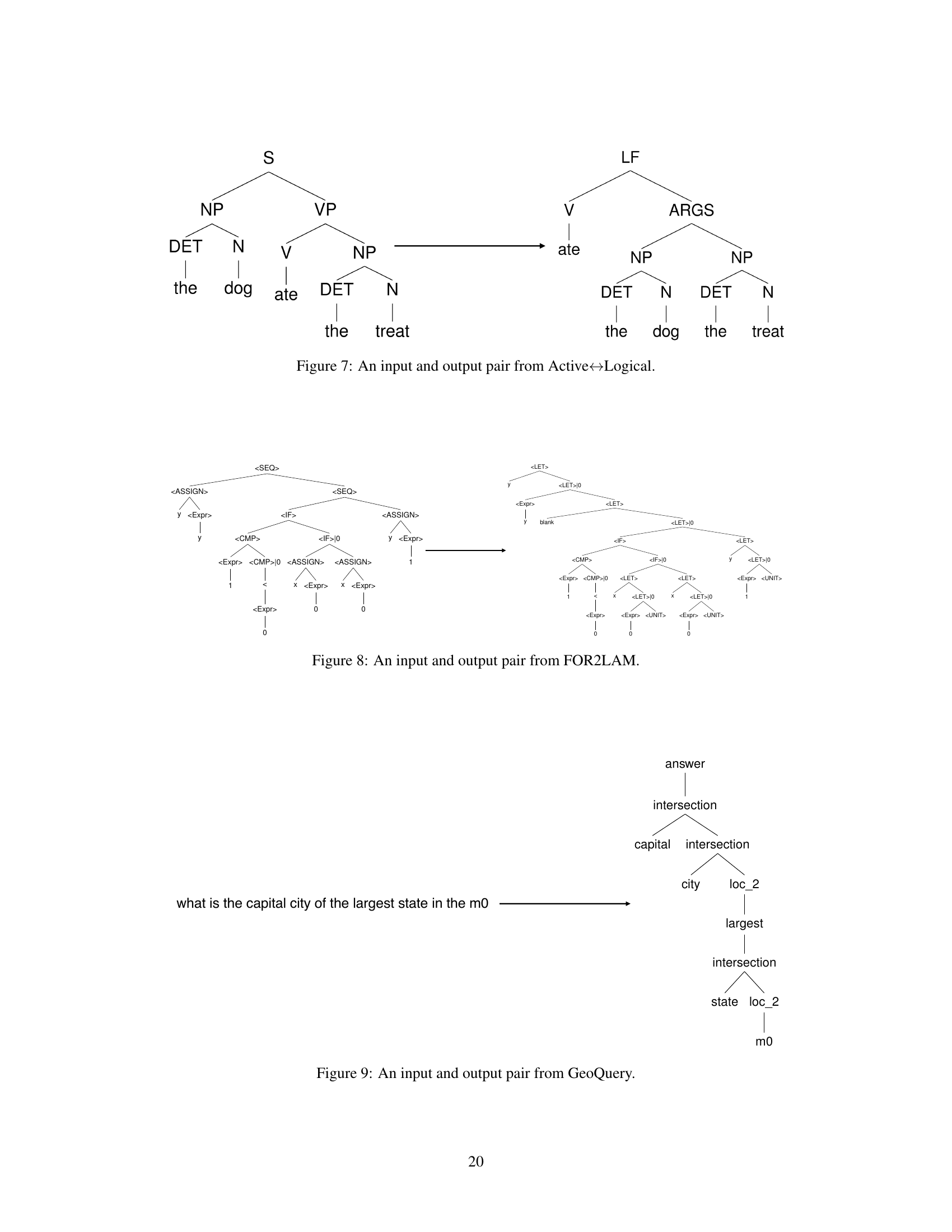
This figure shows an example of input and output pairs for the Active-Logical task. The input is a parse tree representing the sentence ‘The dog ate the treat’ in standard syntactic structure. The output is a parse tree representing the same semantic information, but in a logical form. This demonstrates the model’s ability to transform between active voice and logical form representations of the same sentence.

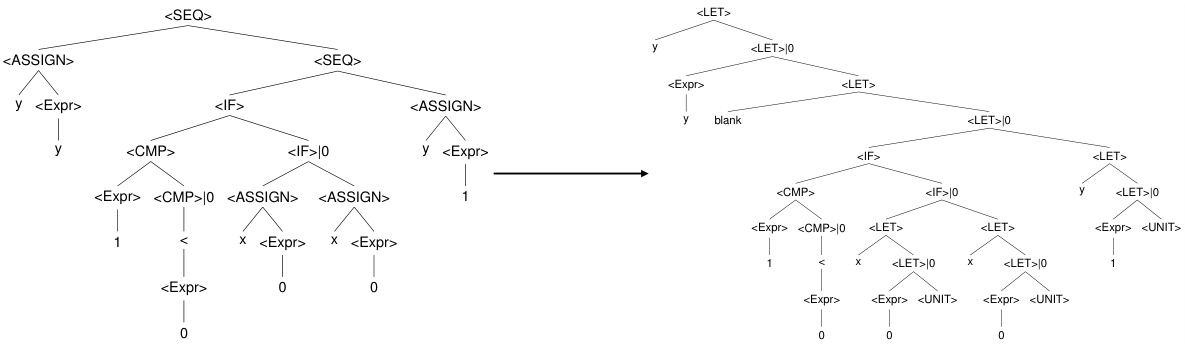
This figure demonstrates the operations of ’left’ and ‘right’ on Sparse Coordinate Trees (SCT). The left side shows how these operations are performed on an example tree, modifying its structure by shifting subtrees. The right side visually explains the effect of the ’left’ operation, showing how it moves a subtree to become the root node, with indices corresponding to absent nodes being removed from the representation. The figure highlights the efficiency of SCT in vector space compared to traditional tensor product representations by explicitly showing how empty nodes are not explicitly stored.

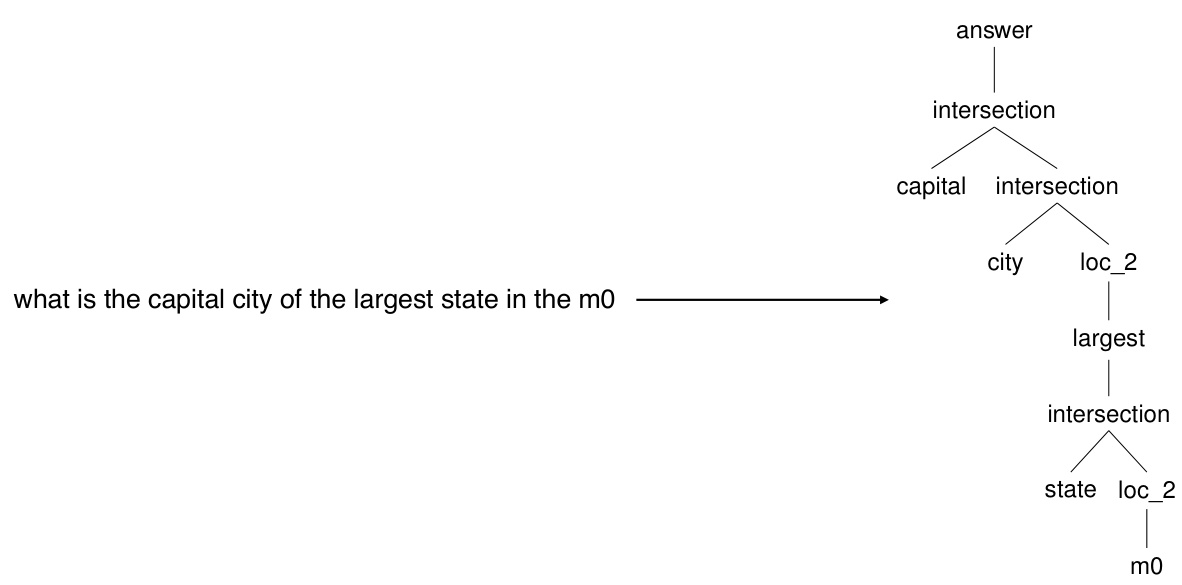
This figure shows an example of input and output pair from the GeoQuery dataset. The input is a natural language question: ‘what is the capital city of the largest state in the m0’. The output is a tree-structured representation of the corresponding SQL query. The tree visually represents the compositional structure of the query, breaking down the question into smaller, more manageable components.

More on tables

This table presents the results of an experiment comparing the performance of different models on the Active↔Logical task, which involves transforming trees between active and logical forms. The models compared include a standard Transformer, a Relative Universal Transformer, NQG (a hybrid neurosymbolic system), and two versions of the Differentiable Tree Machine (DTM): the original and a sparse version (sDTM). The table shows accuracy scores on three test sets: IID (in-distribution), 0-shot lexical (out-of-distribution with unseen words), and structural (out-of-distribution with unseen tree structures). It also displays model parameters, memory usage, and relative speed. The results demonstrate the superior performance of the DTM models, especially the sparse variant, in handling out-of-distribution data.

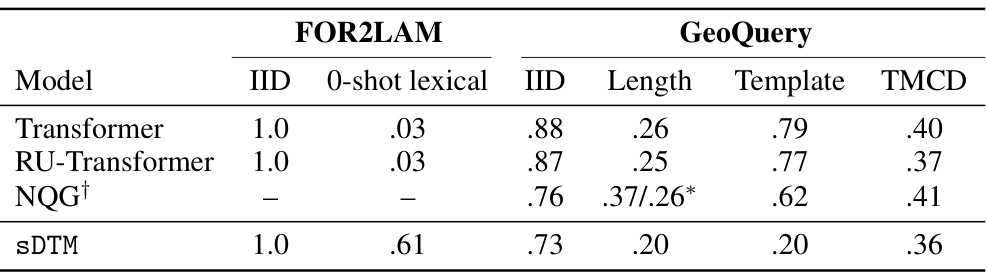
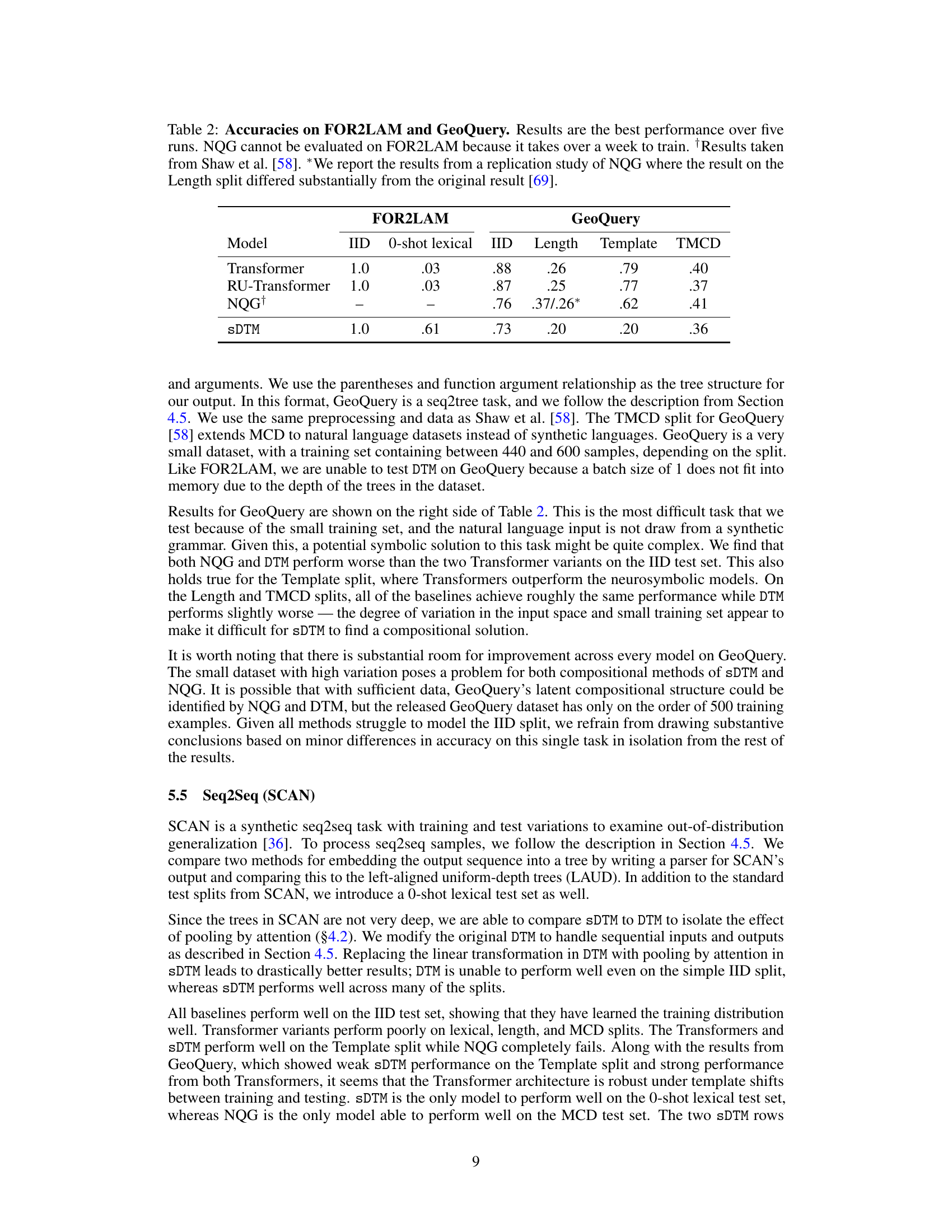
This table presents the results of four different models (Transformer, RU-Transformer, NQG, and sDTM) on two datasets (FOR2LAM and GeoQuery) with various evaluation splits. FOR2LAM is a tree-to-tree program translation task that measures generalization abilities of the models. GeoQuery is a natural language to SQL dataset focusing on compositional generalization abilities of the models. The various evaluation splits evaluate models ability to perform in different out-of-distribution conditions, such as zero-shot and one-shot lexical samples, structural and length generalization, and template generalization. The results show that sDTM is comparatively more robust against out-of-distribution shifts compared to other models in most cases.

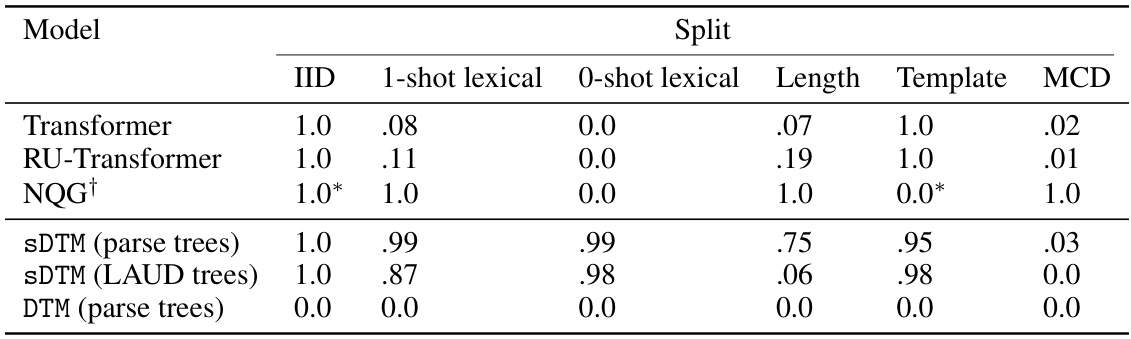
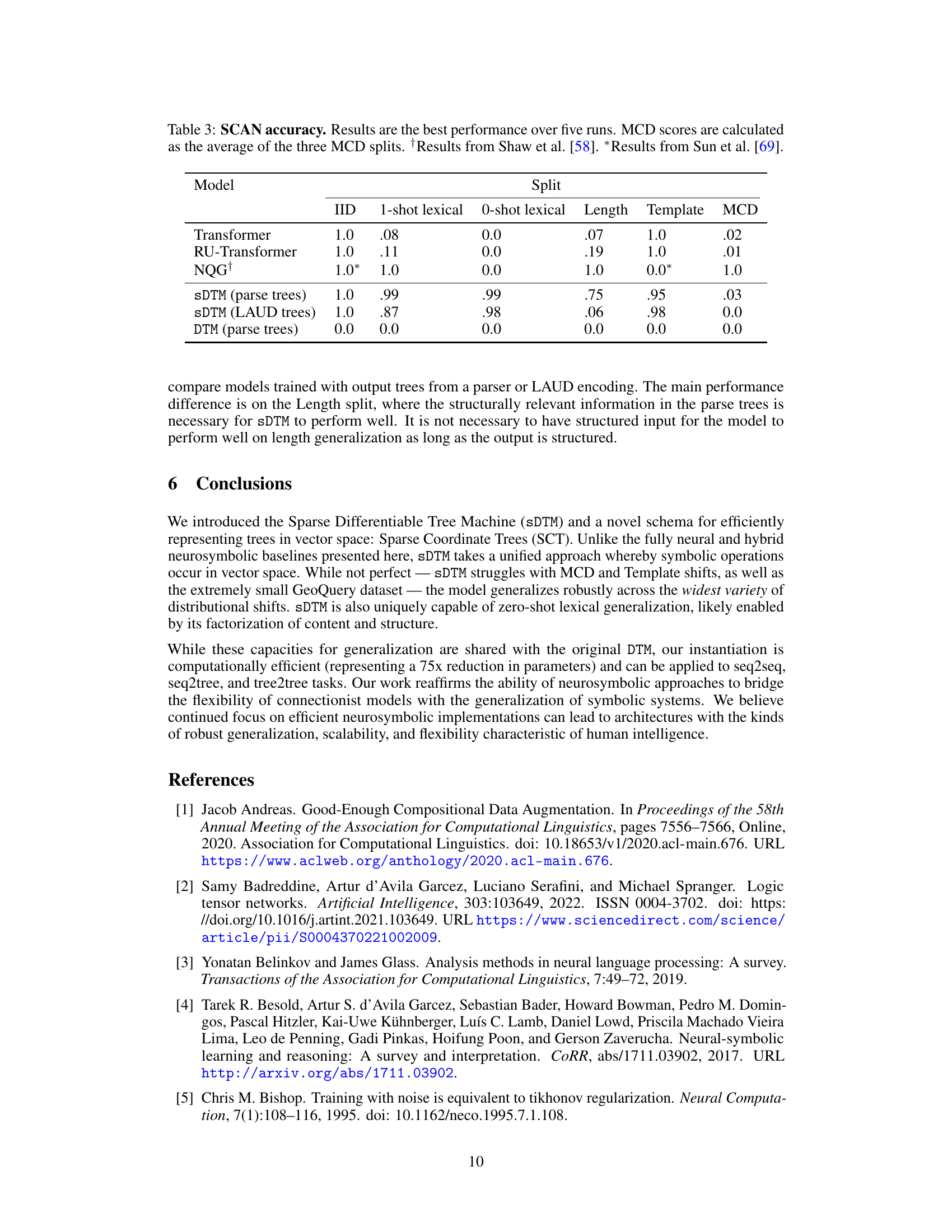
This table presents the accuracy results of different models on the SCAN dataset across various data splits: IID (in-distribution), 1-shot lexical, 0-shot lexical, Length, Template, and MCD (maximum compound divergence). The models compared are Transformer, RU-Transformer, NQG (a hybrid neurosymbolic model), sDTM with parse trees, sDTM with LAUD (Left-Aligned Uniform Depth) trees, and DTM (the original Differentiable Tree Machine). The table highlights the performance of each model in handling different out-of-distribution shifts, showcasing the strengths and weaknesses of each approach in compositional generalization. The MCD scores represent the average accuracy across three different MCD splits.

This table presents the results of an experiment comparing the performance of the Sparse Differentiable Tree Machine (sDTM) model on the SCAN dataset with and without lexical regularization. The experiment focuses on one-shot lexical out-of-distribution generalization. The table shows the accuracy of the sDTM model when trained with and without adding noise to the token embeddings, a form of regularization. The LAUD (Left-Aligned Uniform Depth) method was used to embed the output sequence into a tree structure for processing. The results demonstrate a significant improvement in accuracy when lexical regularization (noise) is used.

This table presents the results of the Active↔Logical experiment, comparing the performance of various models including the original DTM, sDTM (with and without pruning), Transformer, RU-Transformer, and NQG. The performance is measured across three data splits: IID (in-distribution), 0-shot lexical (out-of-distribution with unseen words), and structural (out-of-distribution with novel syntactic structures). The table also shows the model parameters, memory usage, and relative speed, highlighting the significant efficiency gains achieved by sDTM compared to the original DTM.

This table presents the mean and standard deviation of accuracies achieved by the sDTM model on two tasks: FOR2LAM and GeoQuery. FOR2LAM is a tree-to-tree program translation task and GeoQuery is a natural language to SQL query task. The results are broken down by dataset split (IID, 0-shot lexical, Length, Template, TMCD) to show performance under different generalization settings.

This table presents the performance of three different models (sDTM with parse trees, sDTM with LAUD trees, and DTM with parse trees) on the SCAN dataset across various data splits. The splits represent different out-of-distribution scenarios (1-shot lexical, 0-shot lexical, length, template, MCD). The mean and standard deviation accuracies are reported for each model and split, showing the variability in performance across different runs.

Full paper

#