↗ OpenReview ↗ NeurIPS Proc. ↗ Chat
TL;DR#
Estimating convergence rates for general state-space Markov chains is a fundamental yet notoriously difficult problem in various fields. Traditional methods struggle to provide useful bounds for realistic scenarios. This often hinders the development and optimization of algorithms and systems involving Markov chains. This is particularly challenging in stochastic optimization and machine learning applications.
This paper introduces the Deep Contractive Drift Calculator (DCDC), a novel sample-based algorithm to address the limitations of existing approaches. DCDC uses a neural network to solve the Contractive Drift Equation (CDE), which is derived from a new single-condition convergence analysis framework. By solving the CDE, DCDC generates explicit convergence bounds in Wasserstein distance for realistic Markov chains. The paper analyzes the algorithm’s sample complexity and demonstrates its effectiveness on various real-world examples. This represents a significant advance in computational Markov chain convergence analysis.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working with Markov chains because it introduces a novel, general-purpose algorithm for bounding convergence rates, a long-standing challenge in the field. The Deep Contractive Drift Calculator (DCDC) leverages deep learning to address limitations of traditional methods, making convergence analysis more accessible for complex, real-world systems. This opens avenues for improved algorithm design, system optimization, and theoretical advancements in various application domains.
Visual Insights#
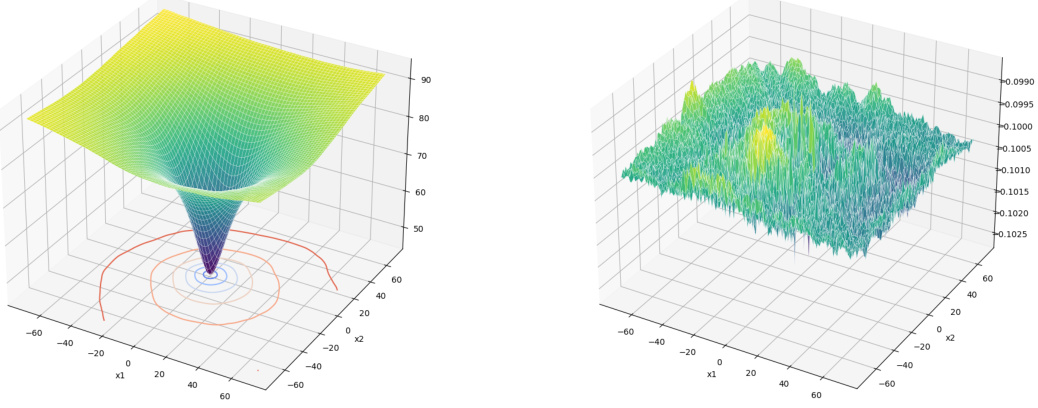
The figure shows the learned solution V (left) and the estimated difference KV-V (right) obtained using DCDC for a mini-batch SGD with L2 regularization applied to logistic regression. The left panel displays a 3D surface representing the learned solution V, which is approximately a wedge-shaped function. The right panel shows the difference between KV and V, which ideally should be close to -0.1 to accurately solve the CDE. The small standard deviation indicates that the neural network is able to accurately approximate the CDE solution.
In-depth insights#
DCDC Algorithm#
The Deep Contractive Drift Calculator (DCDC) algorithm is a novel approach to estimate the convergence rates of Markov chains. Its core innovation lies in leveraging neural networks to solve the Contractive Drift Equation (CDE), transforming a traditionally challenging analytical problem into a computationally tractable one. This allows DCDC to generate convergence bounds, particularly in Wasserstein distance, for complex, high-dimensional Markov chains where traditional methods often fall short. The algorithm’s effectiveness stems from its ability to handle the CDE’s integral nature efficiently, directly bridging deep learning and theoretical convergence analysis. Furthermore, DCDC’s sample complexity analysis offers insights into its practical applicability, providing a measure of confidence in the generated bounds. By combining theoretical rigor with computational efficiency, DCDC represents a significant advance in Markov chain convergence analysis, opening the door for more realistic modeling in diverse fields.
Convergence Bounds#
Convergence bounds in Markov chains are crucial for quantifying the rate at which a chain approaches its stationary distribution. This is vital for establishing the reliability and efficiency of stochastic systems and algorithms. Traditional methods, often relying on drift and minorization conditions, struggle to provide tight bounds for realistic, high-dimensional chains. The development of novel techniques, such as the Deep Contractive Drift Calculator (DCDC), is a significant advancement. DCDC leverages deep learning to solve the Contractive Drift Equation (CDE), offering a sample-based approach for bounding convergence in Wasserstein distance, a metric often more suitable than total variation distance in high dimensions. The algorithm’s strength lies in its ability to handle complex, less structured Markov chains. The sample complexity analysis of DCDC helps to quantify the algorithm’s efficiency and reliability. Furthermore, the approach provides a means to obtain bounds with both exponential and polynomial rates, depending on the properties of the Markov chain. The ability of DCDC to recover exact convergence rates in certain settings highlights its potential for advancing our understanding and analysis of Markov chain convergence.
Sample Complexity#
The sample complexity analysis is crucial for evaluating the practicality of the Deep Contractive Drift Calculator (DCDC). The authors address this by analyzing the number of samples needed from the Markov chain and the number of points required for uniformly sampling the state space to achieve a desired level of accuracy in approximating the solution to the Contractive Drift Equation (CDE). Theorem 5 provides bounds on both the sample size (N) and the number of points (M) needed to guarantee that the approximate solution is within a specified error with high probability. The sample complexity analysis is shown to scale efficiently with problem dimension (d), indicating practical applicability even in high-dimensional settings. Importantly, the analysis supports the method’s capacity to accurately estimate convergence rates by considering the implications of approximate solutions for both exponential and polynomial convergence bounds.
Numerical Examples#
The ‘Numerical Examples’ section likely showcases the practical application of the proposed methodology. It would ideally present results for several distinct Markov chains, demonstrating the algorithm’s versatility and effectiveness across diverse scenarios. These could encompass chains arising from various fields like operations research (e.g., queueing networks, stochastic processing networks), or machine learning (e.g., stochastic gradient descent for different models). Each example should clearly state the problem, experimental setup (including parameter choices and the reasons behind them), and the resulting convergence bounds obtained using the new algorithm. A crucial aspect is comparing the obtained bounds to any existing analytical results or other state-of-the-art methods. This comparison would validate the algorithm’s accuracy and highlight its advantages in handling complex problems where traditional methods struggle. Finally, visualizations (e.g., plots of convergence rates or learned functions) can significantly enhance understanding and add value to the section, making the results more intuitive and accessible to a broad audience. The examples’ diversity and thorough analysis should ultimately bolster confidence in the algorithm’s reliability and practicality.
Future Directions#
Future research directions stemming from this Deep Contractive Drift Calculator (DCDC) work could explore several key areas. Extending DCDC to non-compact state spaces is crucial for broader applicability, perhaps by combining DCDC with techniques for handling unbounded chains or incorporating adaptive sampling strategies focused on regions of interest. Improving the efficiency of the neural network solver remains important, potentially through architectural innovations or more sophisticated optimization techniques, to reduce computational cost for high-dimensional problems. Furthermore, developing theoretical guarantees on the accuracy and sample complexity of DCDC under less restrictive assumptions would enhance confidence in the generated bounds. Finally, investigating the application of DCDC in different domains is important. This includes exploring its use with more complex Markov chains arising in machine learning (e.g., beyond SGD) and operations research problems and exploring its potential for use in applications requiring safety guarantees and assessing risk, by establishing convergence rates for stochastic control systems. The integration of DCDC with other deep learning techniques could prove particularly fruitful.
More visual insights#
More on figures

The figure shows the results of applying the Deep Contractive Drift Calculator (DCDC) algorithm to a tandem fluid network. The left panel displays the learned solution V of the Contractive Drift Equation (CDE), KV - V = -0.1. This solution represents a Lyapunov function that provides an explicit convergence rate for the network. The right panel shows the estimated difference between KV and V, demonstrating the accuracy of the learned solution in approximating the CDE. The close match between the left and right panels indicates a successful solution of the CDE.
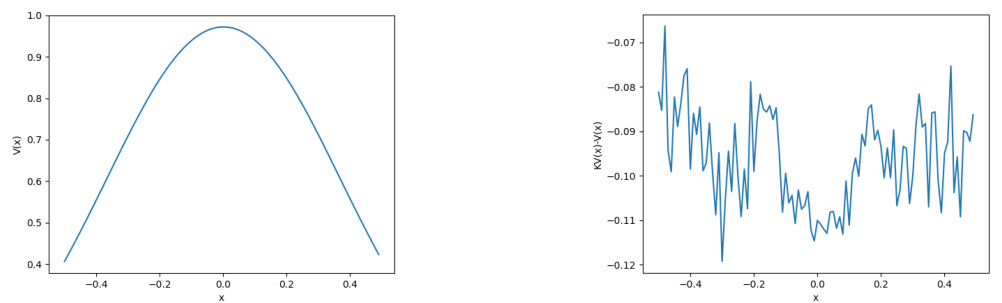
This figure shows the results of applying the Deep Contractive Drift Calculator (DCDC) to a regulated random walk. The left panel displays the learned Lyapunov function V, which is a solution to the Contractive Drift Equation (CDE), KV-V = -0.1. Note the upside-down A-shape, which is different from the V-shapes typically observed in other Markov chains. The right panel shows the difference between KV and V, demonstrating the accuracy of the DCDC solution; the values are close to -0.1, indicating a good fit to the CDE.
Full paper#