↗ OpenReview ↗ NeurIPS Proc. ↗ Chat
TL;DR#
Federated learning (FL) faces challenges, especially with primal-dual methods in non-convex scenarios. A major issue is “dual drift,” where inactive clients’ outdated dual variables cause instability and hinder training efficiency when reactivated. This is especially pronounced under partial client participation, a common strategy in FL to manage bandwidth limitations.
To overcome this, the authors propose A-FedPD. This method cleverly constructs virtual dual updates for inactive clients, effectively aligning their dual variables with the global consensus. This maintains up-to-date dual information even for long-dormant clients. The comprehensive analysis demonstrates A-FedPD’s superior convergence rate and generalization performance in smooth non-convex objectives, validated by experiments on various FL setups. A-FedPD significantly improves the efficiency and stability of federated primal-dual learning
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in federated learning because it addresses the critical issue of “dual drift” in primal-dual methods, a common problem hindering the performance and stability of these methods. By proposing A-FedPD, it offers a novel solution to significantly improve efficiency and generalization, potentially shaping the future of FL algorithms.
Visual Insights#
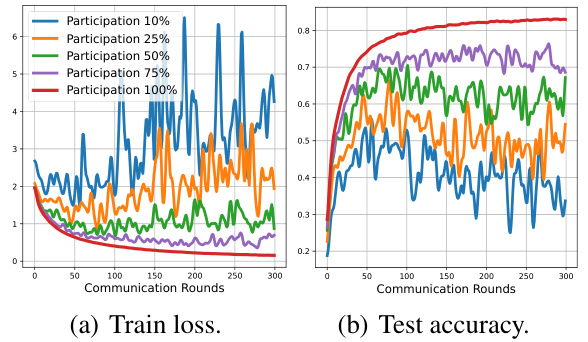
This figure shows how the performance of federated primal dual methods changes with different participation ratios in federated learning. The left graph shows that as the participation ratio decreases, the training loss increases significantly. The right graph shows that the test accuracy also decreases as the participation ratio decreases. This indicates a serious problem called ‘dual drift’, which causes instability and divergence in federated primal dual methods under partial participation.
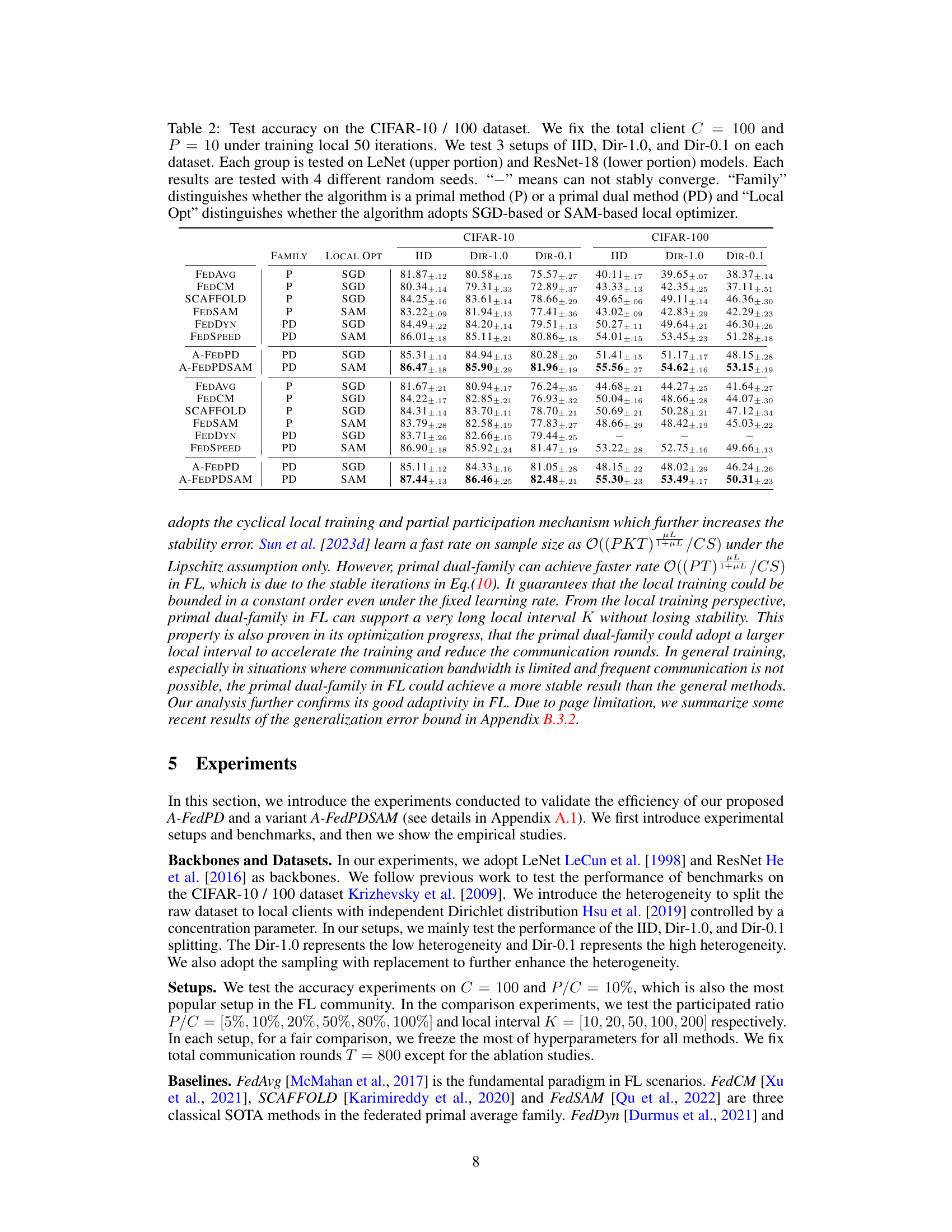
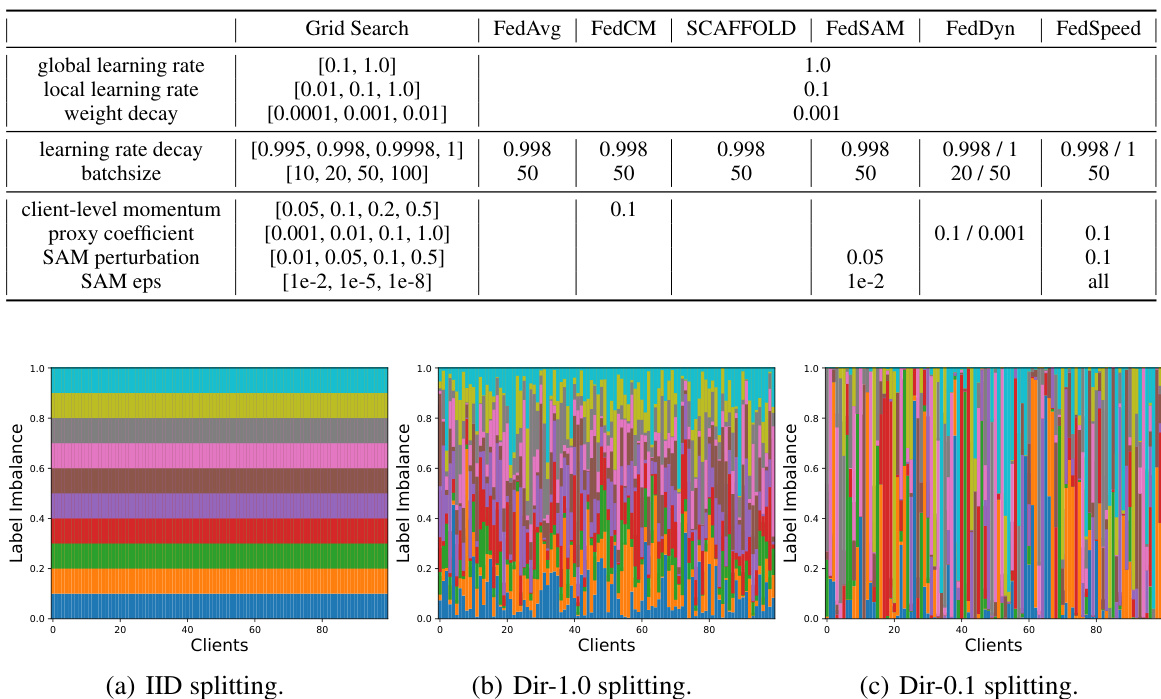
This table presents the test accuracy results on CIFAR-10 and CIFAR-100 datasets using different federated learning algorithms under various data distributions (IID, Dir-1.0, Dir-0.1). The table compares primal and primal-dual methods, along with SGD and SAM optimizers, showcasing their performance under different settings. The results are averaged across four random seeds.
In-depth insights#
Dual Drift in FL#
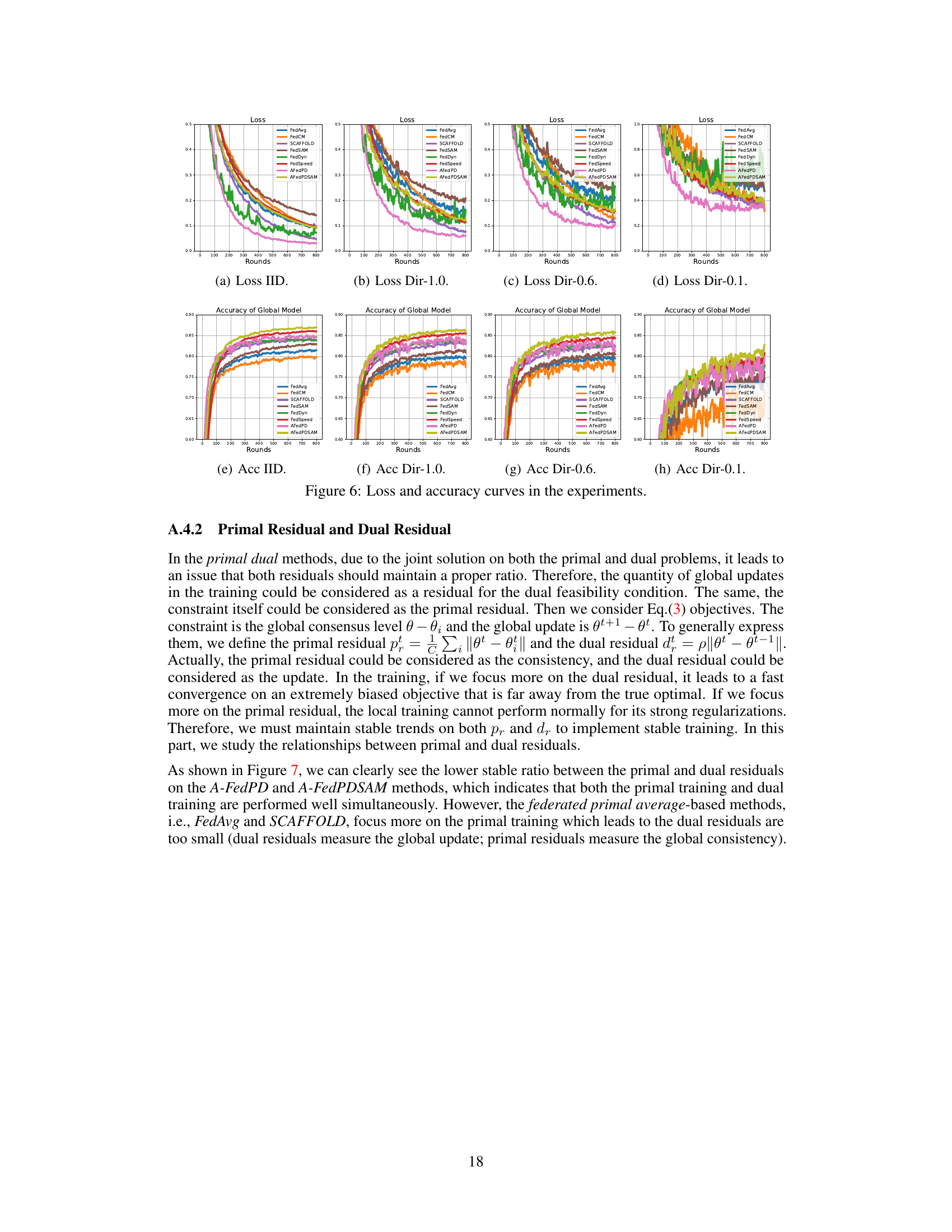
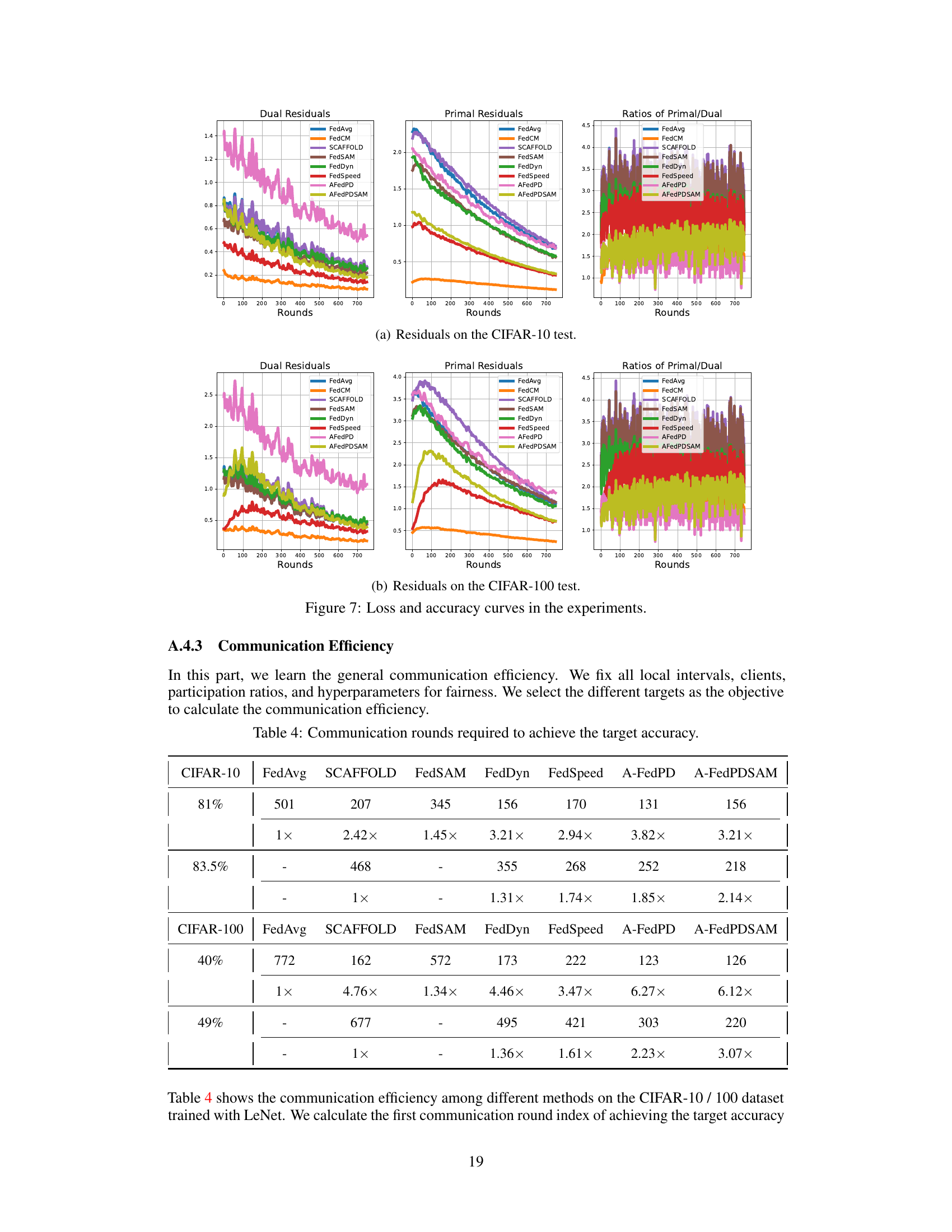
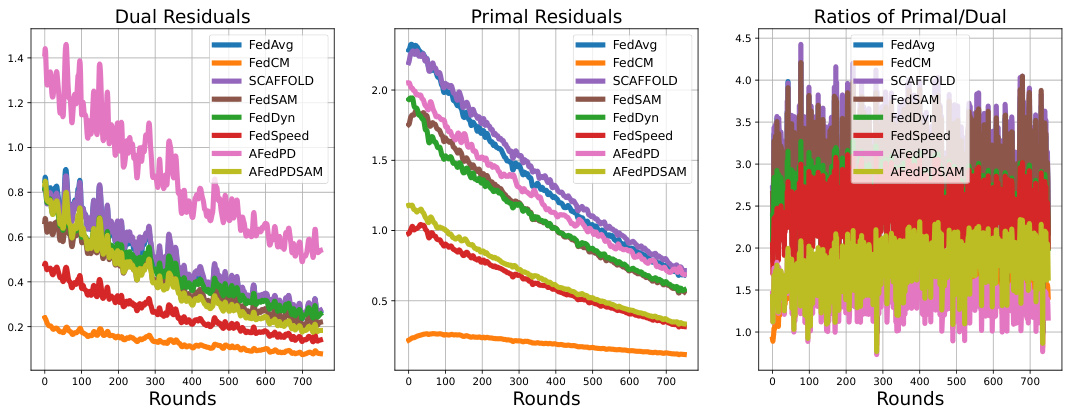
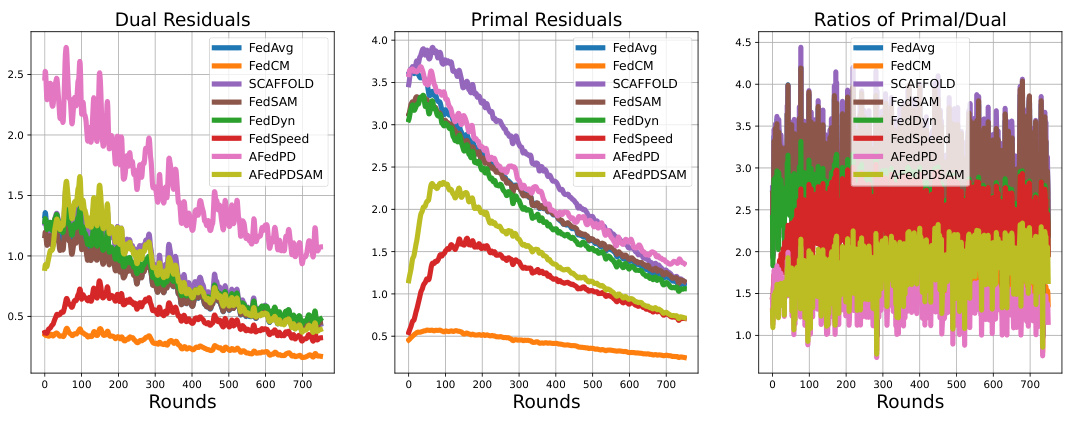
The concept of “Dual Drift” in Federated Learning (FL) arises from the inherent challenges of coordinating multiple clients with potentially outdated or inconsistent information. The core issue lies in the asynchronous updates of primal and dual variables across clients, especially when employing partial participation strategies. Inactive clients, due to limited bandwidth or other constraints, lag in their updates, leading to a discrepancy between their local dual variables and the globally aggregated primal variables. This discrepancy, termed “dual drift,” can significantly hinder convergence and even cause the training process to diverge. The severity of the dual drift is amplified by non-convex objectives and low participation rates. Addressing dual drift is crucial for improving the robustness and stability of FL algorithms. This necessitates innovative approaches that can effectively manage the discrepancies between local and global model parameters across diverse client states. The introduction of virtual updates or similar strategies might be helpful to keep the global model aligned with long-inactive clients. Efficient and stable FL algorithms are essential to realize the full potential of FL, particularly in resource-constrained environments, necessitating further research into tackling the dual drift problem.
A-FedPD Method#
The A-FedPD method tackles the “dual drift” problem in federated learning, a critical issue arising from inconsistent dual variable updates among infrequently participating clients. The core innovation lies in constructing virtual dual updates to align with the global consensus for inactive clients. This clever strategy effectively simulates a quasi-full participation scenario, mitigating the instability caused by outdated dual variables. By aligning local and global dual variables, A-FedPD improves model convergence and stability, especially beneficial when client participation is sparse. This innovative approach significantly enhances the robustness and efficiency of federated primal-dual methods, particularly in challenging, real-world settings.
Theoretical Analysis#
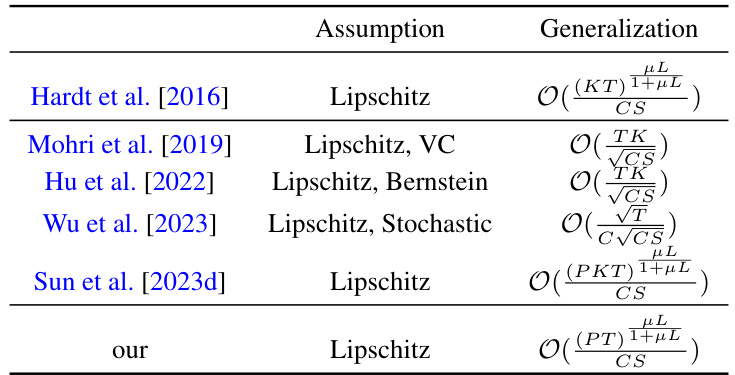
The Theoretical Analysis section of a research paper typically delves into the mathematical underpinnings of the proposed method or model. In the context of a federated learning paper, this section would likely focus on convergence rates, generalization bounds, and optimization efficiency. A rigorous theoretical analysis would involve stating precise assumptions about the data distribution, model characteristics (e.g., convexity or smoothness), and the optimization algorithm. The key goals would be to prove that the algorithm converges to a solution, to bound the error rate, and to demonstrate optimality or near-optimality properties. The analysis might use techniques from optimization theory, statistical learning theory, or information theory, depending on the specific problem and techniques used. The results of this analysis provide important insights into the algorithm’s behavior, establishing confidence in its performance and guiding future improvements. The clarity and completeness of the proofs directly impact the credibility and rigor of the paper.
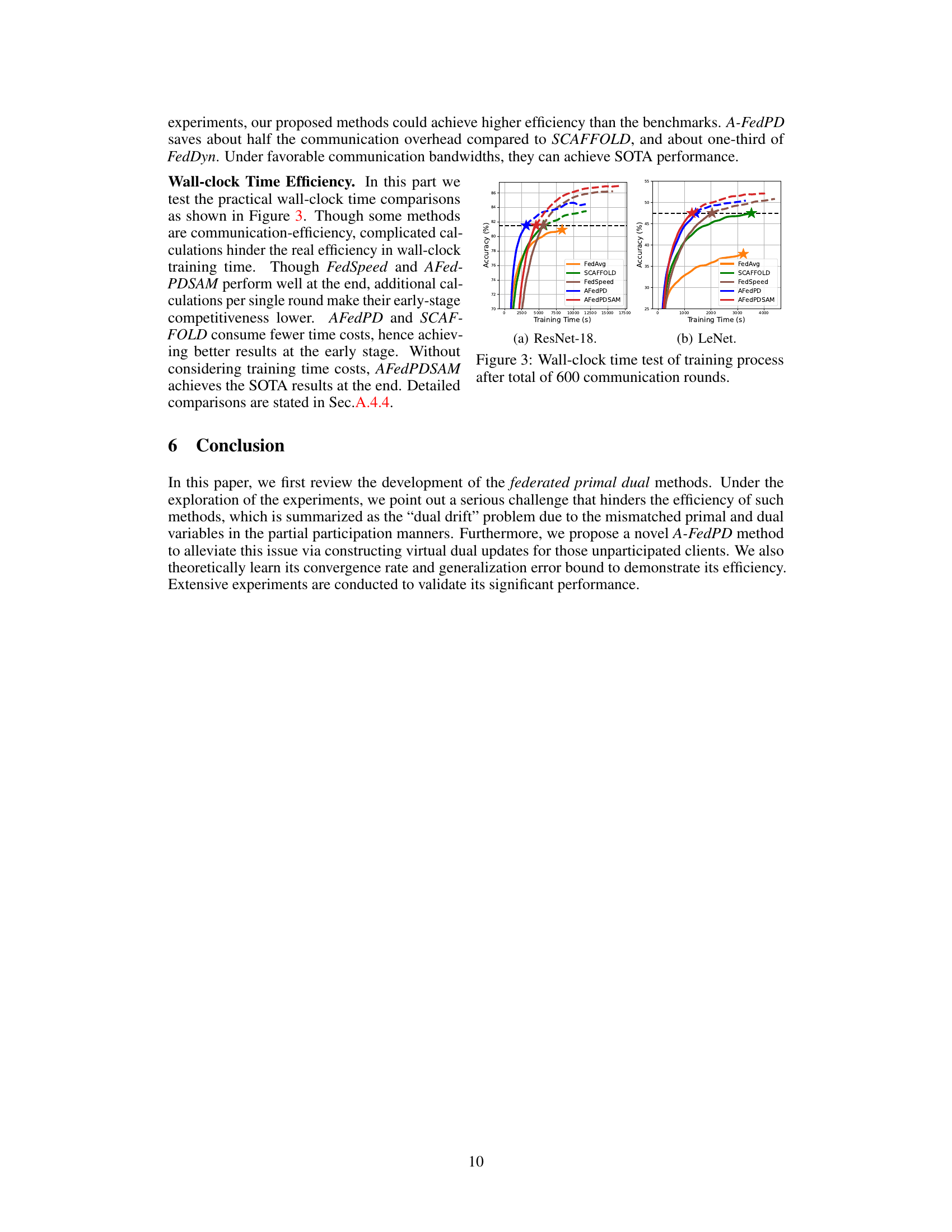
Empirical Results#
The empirical results section of a research paper is crucial for validating the claims made in the paper. A strong empirical results section will present results clearly and concisely, using appropriate visualizations such as graphs and tables. Key performance metrics should be chosen carefully to reflect the research questions and be presented in a way that allows readers to easily interpret and understand. Statistical significance should be clearly stated. A comparison to baseline methods is essential to demonstrate the novelty and impact of the work. The methodology used to conduct the experiments, including the dataset, parameters, and evaluation criteria, should be fully described to ensure the reproducibility of the results. In addition to reporting the primary results, a discussion of any unexpected or anomalous results is important to provide a complete and nuanced view of the findings. Finally, a thoughtful consideration of the limitations of the study is important to inform readers of the scope of the conclusions that can be drawn from the results. A discussion of the broader implications of the study should conclude the section.
Future Works#
Future research directions stemming from this A-FedPD method could explore several promising avenues. Extending the virtual dual update mechanism to handle more complex scenarios, such as those with significant concept drift or highly non-IID data distributions, would significantly broaden the method’s applicability. Investigating the theoretical guarantees for such extensions is crucial. Developing adaptive techniques for determining optimal values of hyperparameters (like the penalty coefficient ρ and local training steps K) would improve A-FedPD’s efficiency and robustness across diverse settings. This could involve exploring reinforcement learning or Bayesian optimization methods. A focused study on the impact of communication efficiency is warranted. While A-FedPD aims to reduce communication overhead, a rigorous comparison against other state-of-the-art federated learning methods under various network conditions would be beneficial. Finally, exploring the integration of A-FedPD with other advanced techniques in FL (e.g., model compression, differential privacy, or personalization) could result in even more efficient and privacy-preserving systems. Investigating the generalization performance benefits of such integrations would also be valuable.
More visual insights#
More on figures

This figure shows the results of experiments conducted to evaluate the performance of the proposed A-FedPD method under various conditions. Specifically, it illustrates how the method performs with different client participation ratios (a), varying local training iteration numbers (b), and changing the total number of communication rounds (c). The consistent performance across these variations highlights the robustness and efficiency of A-FedPD.
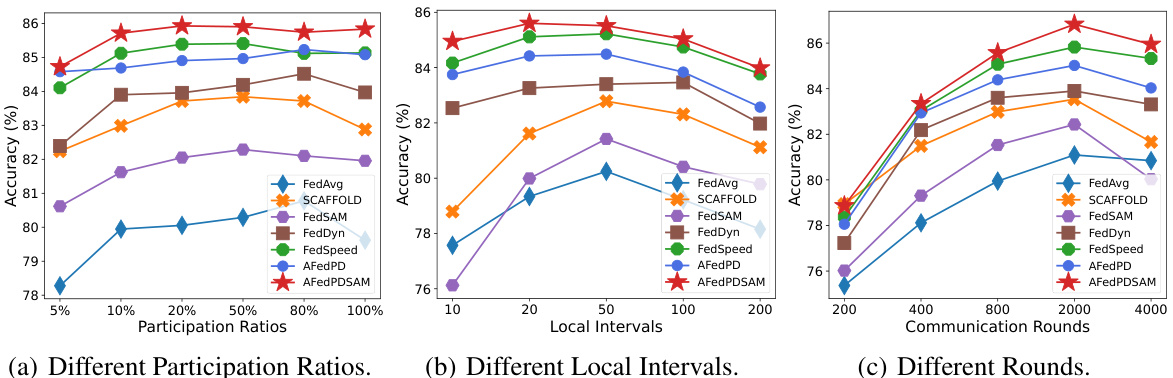
The figure displays three graphs showing the performance of the A-FedPD method under varying experimental conditions. The first graph demonstrates the effects of different participation ratios on the model’s accuracy. The second graph displays the results under different local training intervals. Finally, the third graph illustrates the performance across various communication rounds. In all three cases, the A-FedPD method is compared to other relevant baselines to show the performance improvements.
This figure displays the performance of the A-FedPD model under varying experimental conditions. Three subfigures show how accuracy changes with (a) different participation ratios (percentage of clients participating each round), (b) different local intervals (number of local training iterations per client), and (c) different communication rounds (total number of communication rounds). The consistent trend shows that A-FedPD maintains strong performance under various parameters, with some optimal configurations.
The figure shows the impact of different participation ratios, local intervals, and communication rounds on the performance of the A-FedPD method. It illustrates how the model’s accuracy and training loss change with variations in these key hyperparameters, while keeping the total number of training samples and iterations consistent. This helps in understanding the trade-offs between these parameters and their effect on training efficiency and generalization.

This figure illustrates how brightness biases are introduced to different clients in a federated learning setting. The average brightness of each client’s dataset is calculated. Then, Gaussian noise is added to each sample, randomly altering its brightness and one of its color channels. This simulates the real-world scenario of data being collected from various sources with differences in lighting and color balance. The goal is to introduce a level of heterogeneity among clients’ datasets, mimicking real-world conditions.
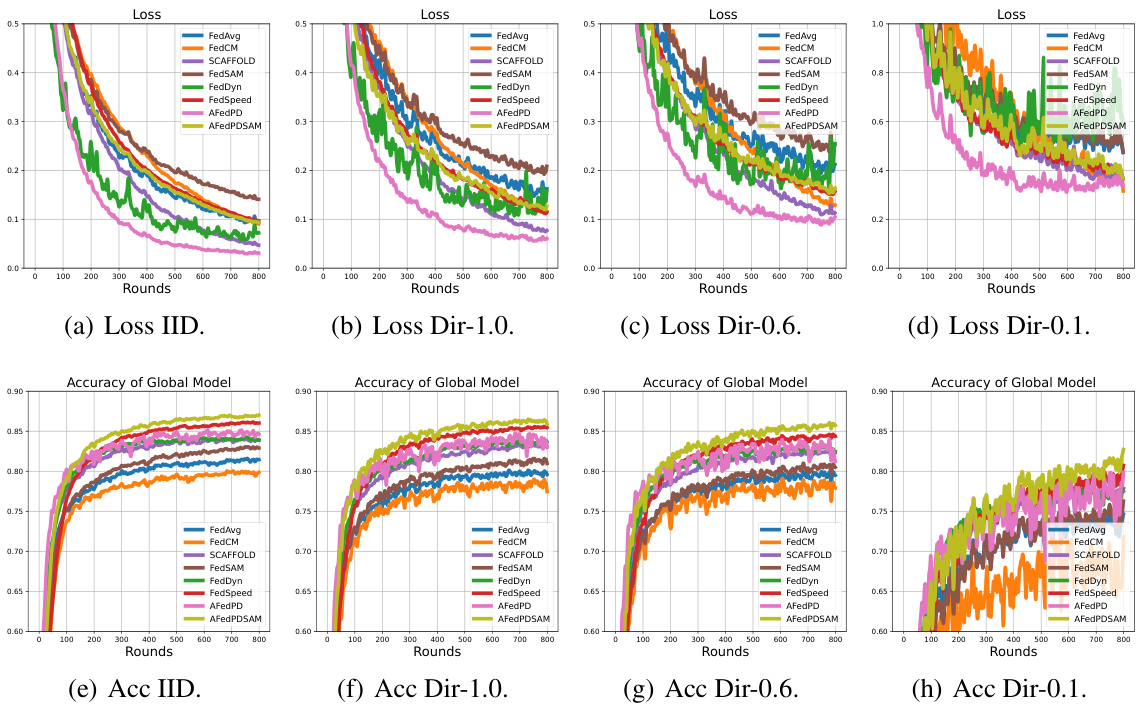
The figure shows three graphs, each illustrating the performance of the A-FedPD model under different settings. The first graph shows the test accuracy at different participation ratios (percentage of clients participating in each training round). The second graph illustrates the impact of varying the local training intervals (number of local updates performed by each client before model aggregation). The third graph compares the model’s performance over a range of communication rounds (number of communication rounds between server and clients). Overall, these graphs highlight the robustness and efficiency of A-FedPD in handling different training scenarios and demonstrate its ability to achieve high accuracy with fewer communication rounds.
This figure displays the results of experiments evaluating the performance of the A-FedPD method under varying conditions. Three sets of experiments are shown, each with a different parameter fixed: (a) Different Participation Ratios: Shows how A-FedPD’s accuracy changes with different percentages of clients participating in each round. (b) Different Local Intervals: Shows how A-FedPD’s accuracy changes with different numbers of local training iterations. (c) Different Rounds: Shows how A-FedPD’s accuracy changes over different communication rounds.
This figure displays the results of experiments conducted to evaluate the performance of the A-FedPD method under varying conditions. The three subplots show how the method performs with different participation ratios (percentage of clients participating in each round), different local intervals (number of local training iterations), and different communication rounds (number of communication rounds between server and clients). In all experiments, the total number of training samples and iterations were kept constant to isolate the effect of the varied parameter. The graphs show that A-FedPD demonstrates consistent and stable performance across different settings.
More on tables
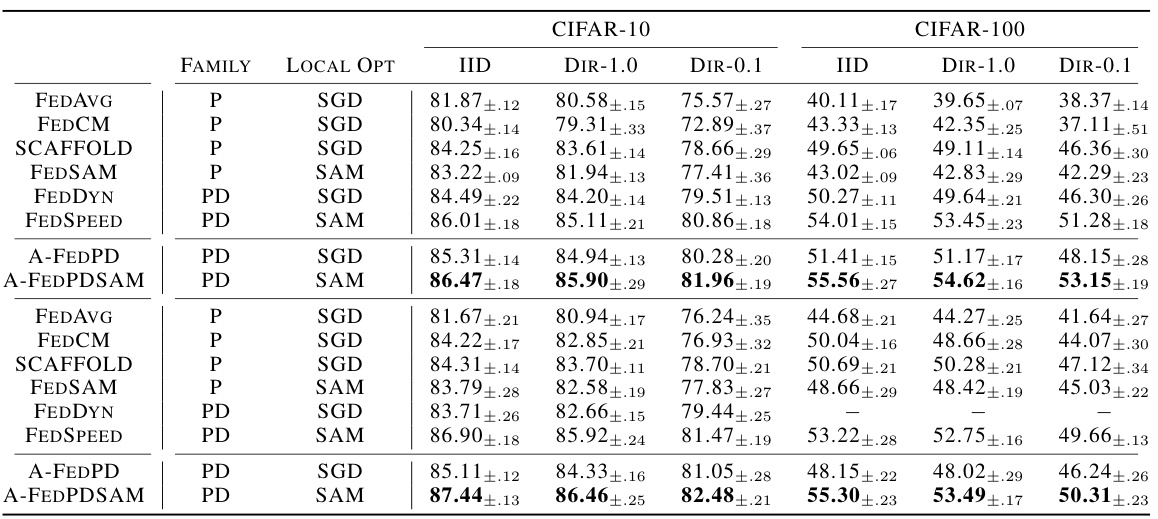
This table presents the test accuracy results on CIFAR-10 and CIFAR-100 datasets for various federated learning algorithms. The experiments use 100 clients, with 10 active clients per round, and 50 local training iterations. Three data distribution scenarios (IID, Dir-1.0, and Dir-0.1) representing different levels of data heterogeneity are evaluated. Results are shown for LeNet and ResNet-18 models, differentiating between primal and primal-dual methods, and using either SGD or SAM as local optimizers. The table highlights the performance variations under different settings.

This table presents the test accuracy results on CIFAR-10 and CIFAR-100 datasets using different federated learning algorithms. The experiments were conducted with 100 total clients, 10 active clients per round, and 50 local training iterations. Three data distributions are compared: IID, Dir-1.0 (low heterogeneity), and Dir-0.1 (high heterogeneity). Both LeNet and ResNet-18 model architectures are used. The table shows the average accuracy and standard deviation (over 4 random seeds) for each algorithm and dataset. The ‘Family’ column indicates whether the algorithm is a primal or primal-dual method, and the ‘Local Opt’ column shows whether the algorithm uses SGD or SAM for local optimization.
This table presents the test accuracy results on CIFAR-10 and CIFAR-100 datasets for various federated learning algorithms. The experiments used 100 clients total, with 10 active clients per round, and 50 local training iterations. Three data distributions (IID, Dir-1.0, Dir-0.1) representing different levels of data heterogeneity were tested with LeNet and ResNet-18 models. The table compares primal and primal-dual methods, and algorithms using SGD or SAM optimizers. A ‘-’ indicates that the algorithm did not converge stably.

This table presents the test accuracy results for different federated learning algorithms on the CIFAR-10 and CIFAR-100 datasets. The experiments used 100 clients, with 10 active per round, and 50 local training iterations. Three data distributions (IID, Dir-1.0, Dir-0.1) were tested. The algorithms are categorized by whether they are primal or primal-dual, and whether they utilize SGD or SAM optimizers. Results are averaged across four random seeds, and a ‘-’ indicates that the algorithm failed to converge.

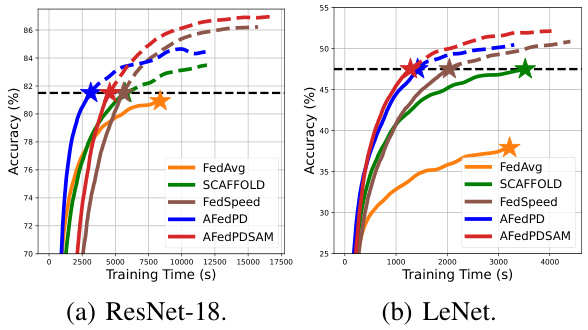
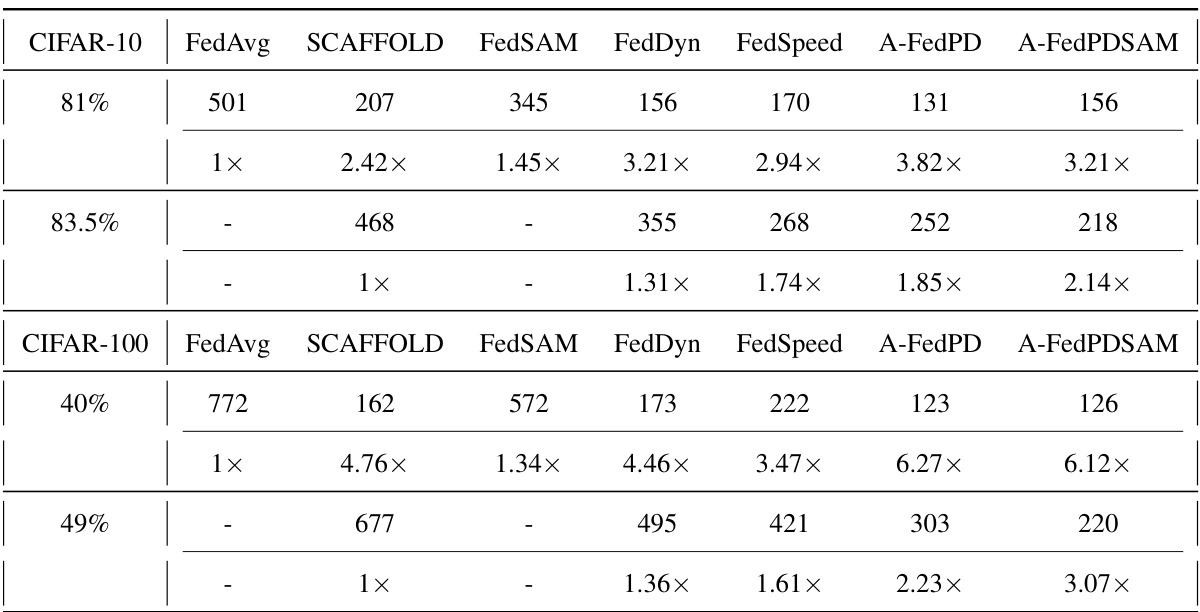
This table presents the wall-clock time in seconds required to train one round (100 iterations) using the LeNet model. It compares the time taken by FedAvg, SCAFFOLD, FedSAM, FedDyn, FedSpeed, A-FedPD, and A-FedPDSAM. The time for FedAvg is used as the baseline (1x), and the times for other methods are expressed relative to that baseline.

This table presents the test accuracy results on CIFAR-10 and CIFAR-100 datasets using various federated learning algorithms. The experiments used 100 clients total, with 10 active in each round and 50 local training iterations. Three data distributions (IID, Dir-1.0, and Dir-0.1) were tested to assess performance under different levels of data heterogeneity. The algorithms are categorized as either primal (P) or primal-dual (PD) methods and whether they use SGD or SAM for local optimization. Results are averaged across four random seeds.

This table presents the test accuracy results on CIFAR-10 and CIFAR-100 datasets for various federated learning algorithms under different data distributions (IID, Dir-1.0, Dir-0.1) and model architectures (LeNet, ResNet-18). The results are categorized by algorithm family (primal or primal-dual) and local optimizer (SGD or SAM). Each result is averaged over four random seeds, and a ‘-’ indicates that the algorithm did not stably converge for that specific setting.
This table presents the test accuracy results on CIFAR-10 and CIFAR-100 datasets using different federated learning algorithms. The experiments used 100 clients in total with 10 active clients per round. Three data distributions are compared (IID, Dir-1.0, Dir-0.1), reflecting varying levels of data heterogeneity. Both LeNet and ResNet-18 are used as model backbones. The table also categorizes methods as primal (P) or primal-dual (PD) and specifies the local optimizer used (SGD or SAM).
Full paper#